基于两种时间序列模型的沈阳市人口死亡率的预测研究*

陈 萌 赵 丽 符文华△

【提 要】 目的 基于时间序列模型对沈阳市月死亡率进行预测研究,为制定人口健康策略提供参考依据。方法 选取Holt-Winter模型与SARIMA模型对沈阳市2010年1月-2021年12月主城区月死亡率进行预测分析,并比较两种模型准确度。结果 沈阳市主城区人口粗死亡率呈上升趋势,分布呈现周期性特征,年初和年末稍高,年中稍低。SARIMA模型的MAPE为4.33%,Holt-Winters相乘模型的MAPE为3.82%,从预测效果来看,验证集的实际值均落在预测值的95%CI之内,SARIMA模型和Holt-Winters相乘模型的总体相对误差分别为1.20%和0.39%。结论 Holt-Winter相乘模型更适于沈阳市月度人口死亡率的预测。

死亡率作为最可信的卫生资料之一,直接反映了人口健康状况和社会卫生水平。了解居民死亡水平及变化趋势,对衡量疾病死亡负担,制定疾病防控策略,配置卫生资源以及评估干预措施效果都有着积极的作用[1]。

资料与方法

1.数据来源

数据来源于沈阳市疾病预防控制中心提供的2010年1月-2021年12月沈阳市主城区人口死亡监测数据。登记对象为沈阳市内五区户籍人口,并以《居民死亡医学证明(推断)书》作为统计凭证。

2.研究方法

以2010年1月-2019年12月数据作为训练集,2020年1月-2021年12月数据作为验证集,比较Holt-Winters与季节性差分自回归移动平均(seasonal autoregressive integrated moving average,SARIMA)模型预测精确度,得出最优模型。最后将验证集数据纳入最终模型,对沈阳市2022-2023年月度死亡率进行定量预测。

(1)模型介绍

Holt-Winters指数平滑模型包含水平项α、趋势项β和季节项γ,参数范围均为0～1之间,是模型预测值与实测反推值之间的平衡权重,参数越小,则模型拟合较好。当季节变化大致保持不变时,常选择加法模型;当季节变化与时间序列的水平成比例变化时,则选择相乘模型[2-3]。

差分整合移动平均回归(autoregressive integrated moving average,ARIMA)模型:ARIMA(p,d,q)中,AR是自回归,p为自回归项数;MA为滑动平均,q为滑动平均项数,d为使序列平稳所做的差分阶数[2-3],SARIMA是由 ARIMA(p,d,q)模型与季节性 ARIMA(P,D,Q)s模型混合而成,二者建模过程基本相似,包括序列平稳化、模型识别、模型检验、模型预测[4]。

(2)统计学方法

采用R 4.1.2软件进行时间序列模型的建立、验证和预测,主要调用“tseries”和“forecast”软件包[5]。模型选择中ets()函数和auto.arima()函数,默认以校正赤池信息准则(AICc)值最小为最优模型[3];比较两模型拟合程度可参考平均绝对百分比误差(MAPE),参数越小表示拟合程度越好。假设检验以P≤0.05认定为具有统计学意义。

结 果

1.流行病学概况

2010-2021年沈阳市主城区年均死亡率为8.65‰,粗死亡率呈现逐步上升后趋于平稳,标化死亡率则呈现逐年下降趋势,见图1。月粗死亡率呈现周期性分布特征,表现为年初和年末稍高,2月稍有降低,6月份最低,7-8月份略有回升,但总体不同月度间死亡率差异较小,图2显示了月度粗死亡率的平均水平。

图1 2010-2021年沈阳市主城区粗死亡率和标化死亡率趋势图

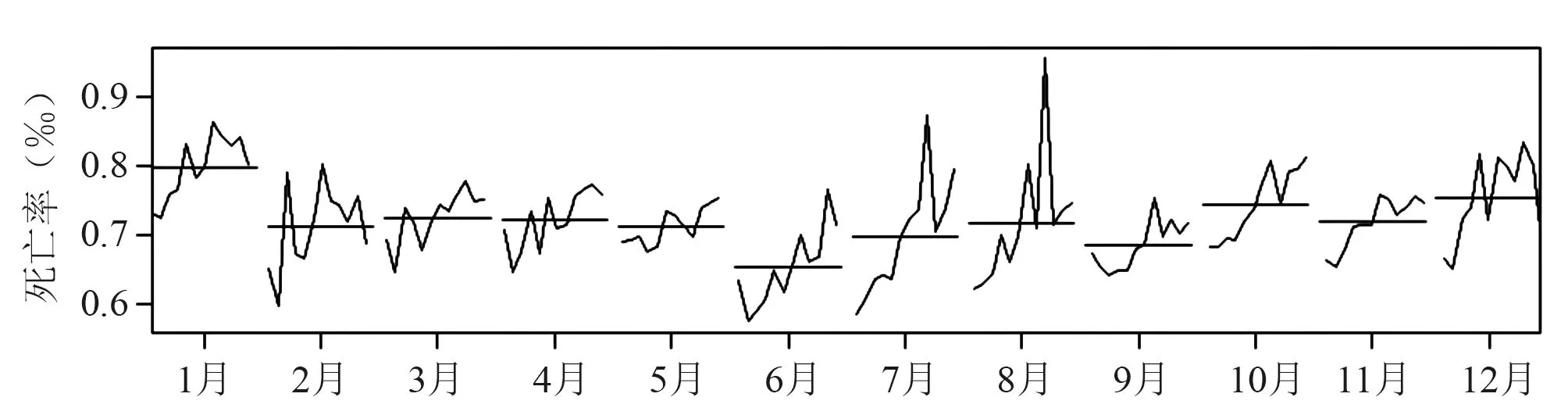
图2 2010-2021年沈阳市主城区月死亡率趋势图

2.建立Holt-Winters模型

使用“stl”函数将死亡率时序图拆分成季节周期、长期趋势和随机序列三部分,见图3。使用ets()函数筛选出最优模型:Holt-Winters相乘模型的水平项α=0.14、季节效应项γ=1×10-4,AICc值为-168.70,MAPE为3.82%。

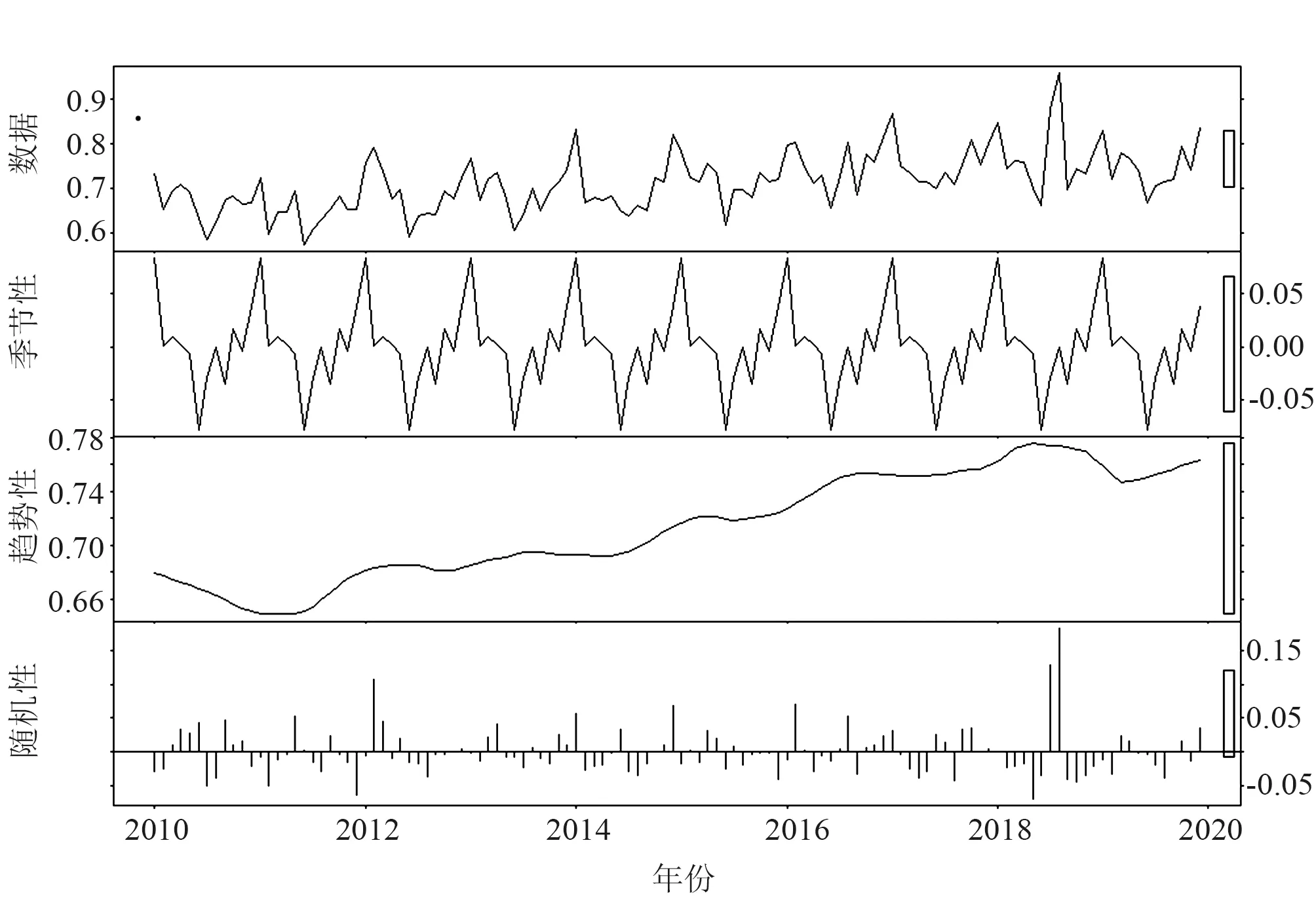
图3 2010-2019年沈阳市主城区人口死亡率时序分解图

3.建立SARIMA模型

使用ndiffs()函数进行差分处理后,结果显示趋势性差分(d=1)时,平衡性检验结果为P=0.01,提示差分后的序列基本趋于平稳。使用auto.arima()函数最终模型确定为SARIMA(4,1,1)(2,0,0)12,AICc值为-390.10,MAPE值为4.33%,应用Ljung-Box检验显示P=0.93>0.05,表明模型残差序列为白噪声序列,模型拟合较好。

4.模型预测和比较

分别运用Holt-Winters相乘模型和SARIMA(4,1,1)(2,0,0)12预测沈阳市2020-2021年的月度死亡率,蓝色曲线为月度死亡率的预测值,阴影部分为预测值的95%CI,见图4。从预测效果来看,两种模型的实际值均落在预测值95%CI之内,SARIMA和Holt-Winters相乘模型的总体相对误差分别1.20%和0.39%,综合来说Holt-Winters相乘模型预测效果较好。

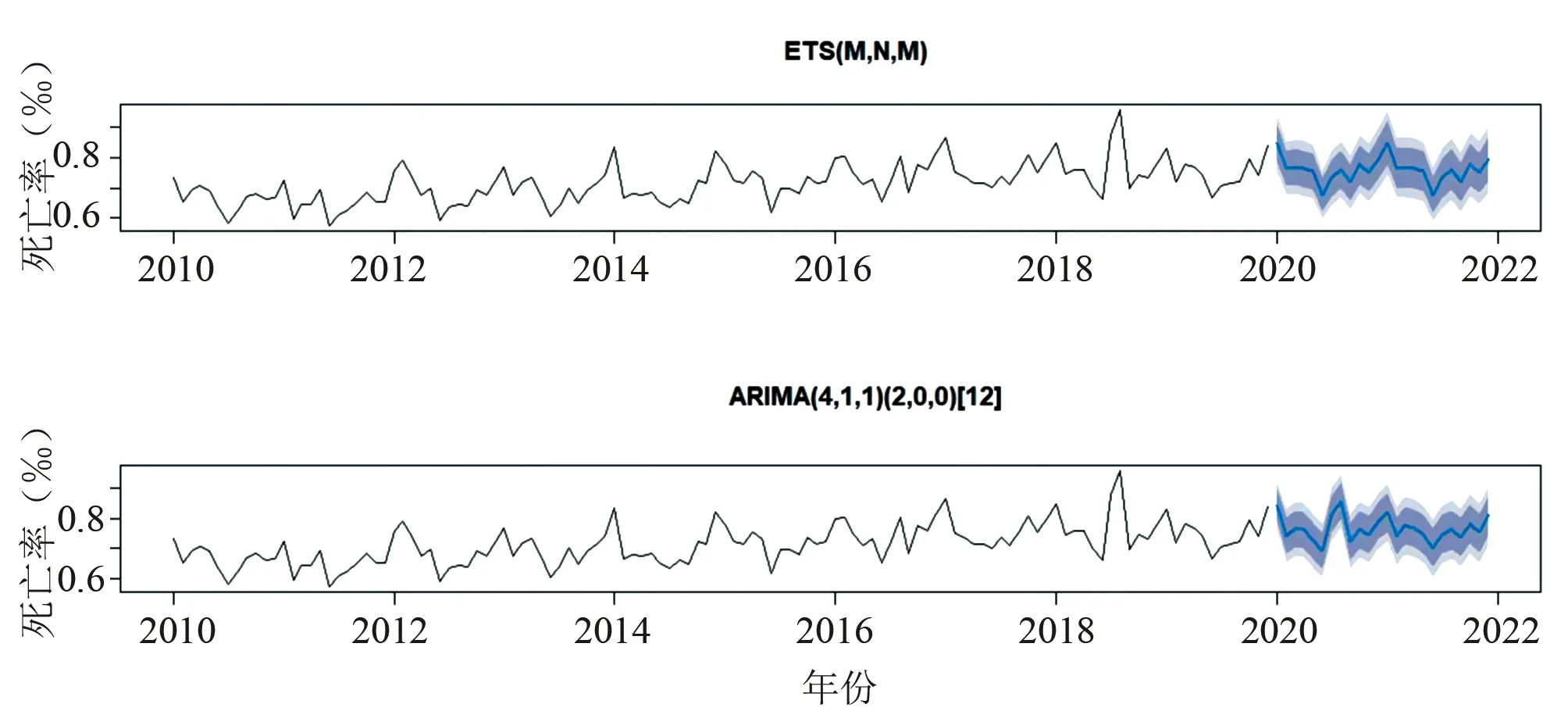
图4 2020-2021年沈阳市主城区人口月死亡率

5.模型应用

将2020-2021年数据重新加入到总数据集中,运用Holt-Winters相乘模型对沈阳市2022-2023年人口月死亡率进行预测,年均死亡率为8.99‰,见图5。

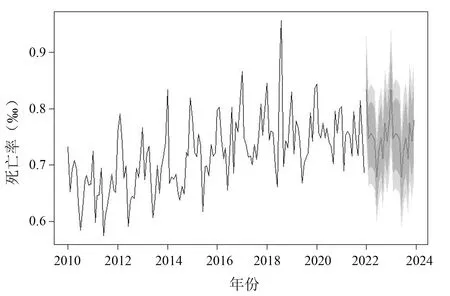
图5 2022-2023年沈阳市主城区月度死亡率预测图

讨 论

当前,我国已经进入人口老龄化快速发展阶段[6],而辽宁省人口老龄化程度则居于全国首位[7],预计到2050年,人口年龄构成将发展成典型的倒金字塔结构[8]。老年人口比例的变化势必会导致死亡率的明显改变,沈阳市的人口发展已经进入了“风险积累”和“风险爆发”并存的阶段,呈现出粗死亡率逐年上升的现象,国内许多研究[9-10]都验证了不同程度的老龄化与死亡密切相关;另一方面随着医疗技术水平的发展,老年人预期寿命不断增加,表现为人口标化死亡率逐年下降。

根据死因监测资料,2021年沈阳市居民死因以慢性非传染性疾病为主,占比约84.44%,全人群死因顺位前3位分别为心脏病、恶性肿瘤和脑血管病。死亡率周期性分析显示年初和年末稍高,2月份略有下降,6月份最低,7-8月份则略有回升的趋势。多项研究表明死亡率和温度之间存在较强的相关性,老年人体温调节敏感度降低,影响更为明显[11-12]。The Lancet Planetary Health发表一项联合研究表明[13],全球每年死亡人数的9.43%都是异常的低温或高温导致的,其中约90%与异常低温有关,结合东北地区冬季较为寒冷的气候特点,年初年尾的心脑血管疾病[14-15]和老年人跌倒[16]等因素致死均有不同程度地增加。反之,日最高气温升高也是诱发心脑血管疾病的危险性因素[15,17],每年7-8月份随着气温升高,死亡率也随之回升。人口死亡率不仅受到自然环境的影响,社会政策等因素对其影响同样较为明显,2020年新冠肺炎全球爆发以来,不同程度的社会和医疗管控,所造成的延迟就医[18]等问题也对死亡率产生了影响。2010-2019年死亡率周期趋势较为一致,2020-2021年则有所变动,从而造成个别月份预测误差较大的问题。

时间序列模型作为预测数据的一种工具,模型选择的种类并不绝对,需要通过不断地整合监测数据、定期调整参数来寻求更为贴近真实情况的模型。由于人口死亡率受到遗传、人口构成、环境和社会等众多因素影响,模型构建应遵循“抓大放小”的原则,注意避免过度追求精确度所造成的过度拟合。

随着我国第一、第二个生育高峰人口相继进入慢性病和死亡的高发期,在未来若干年内,将出现大量“带病生存”人群,还将迎来死亡率快速增长期。人口伤病死亡水平预测的应用在实际决策中具有较高的参考意义,积极采取合适的策略措施,有益于提高人群健康水平和预期寿命。