COVID-19潜伏期分布估计的统计学方法比较*
2023-10-18卓冰婷陈俊宏杜志成郝元涛
刘 裕 卓冰婷 陈俊宏 杜志成 郝元涛
【提 要】 目的 回顾和评估COVID-19潜伏期分布估计的统计学方法,为有效、快速、准确地收集和分析潜伏期数据提供参考和借鉴。方法 利用COVID-19疫情早期发表的数据,比较分析单区间删失、双区间删失和随机过程三类方法不同分布假设下获得的COVID-19潜伏期分布最大似然估计和贝叶斯估计。结果 同类方法不同分布假设间,非参数方法要比参数方法拟合效果更好,但非参数方法存在较多的跳跃点,且无法获得估计的95%置信区间;同类方法相同分布假设条件下,最大似然估计与贝叶斯估计结果和拟合效果相近;同类方法的对数正态假设条件下获得的潜伏期分布的大分位数(>90%分位数)可能较大地偏离非参数估计结果;从数据利用的角度,双区间删失方法对数据的利用率最高;由于数据收集和利用的差异,不同方法得到的潜伏期分布估计可能存在较大差异。结论 采用双区间删失观测的参数模型获取传染病潜伏期分布的最大似然估计,可提高数据的收集、利用和分析效率;仔细比较不同分布假设下参数模型和非参数模型的结果,并谨慎解释潜伏期大分位数的估计结果,将有利于作出正确的防控决策。
传染病的潜伏期是指宿主首次暴露于传染源到其首次出现疾病相关临床表现(体征或症状)的时间间隔[1]。掌握潜伏期分布对病例的定义、传染源的追溯、接触者追踪随访期和隔离期的设置、入境筛查隔离策略的制定、无症状感染人群医学观察期的确定等,以至疫情规模和传播潜力的测算,都具有重要意义[2-4]。
然而,潜伏期分布的准确估计并非易事,我们以新型冠状病毒感染(COVID-19)为例加以说明。首先,COVID-19的感染暴露时间无法直接观测,往往只能知道感染暴露是在某个时间段发生的,也就是说,它是一种区间删失观测(interval censored data)[5]。这也是尽管截至2020年1月22日已报告422例COVID-19确诊患者,但Linton等[6]只纳入10例具有明确暴露日期和发病日期的数据预估COVID-19潜伏期分布的可能原因。其次,感染以后患者出现症状的时间经常不能准确回忆,也就是说,患者出现症状(即发病)的时间也可能是区间删失观测。由于COVID-19疫情发生在冬季,疫情早期人们对该病知之甚少,其临床症状与呼吸道感染重叠,COVID-19确诊患者对首次出现新型冠状病毒(SARS-Cov-2)感染症状的回忆往往摸棱两可。此时,调查得到的暴露感染和症状出现时间经常都是区间删失的情况,即我们获得的是双区间删失观测(doubly interval censored data)[7]。再者,对区间删失尤其是双区间删失观测数据的潜伏期分布估计远比精确观测复杂,结果稳定性也可能更差[8]。自2019年12月发生COVID-19疫情以来,研究人员采用不同的统计学方法分析各自收集的数据估计COVID-19的潜伏期分布,得到其潜伏期中位数在4.0天到7.8天之间[6,9-13],相差较大。而他们获得的COVID-19潜伏期大分位数估计差异更大,这体现在对潜伏期超过14天的患者比例的估计。例如,Bi等[9]估计潜伏期超过14天的COVID-19患者在5%左右,而Qin等[12]的结果显示这个数值超过10%。
分布假设和估计方法对潜伏期的分布估计具有深刻影响[14]。为了加深传染病潜伏期分布的理解,提升潜伏期分布监测中数据收集和利用的效率,我们有必要对现有的分析模型进行评估。本研究旨在综述潜伏期分布估计方法,采用COVID-19疫情早期Lauer等[11]收集的数据对这些方法进行比较,以期为有效、快速、准确地预估潜伏期分布提供参考和借鉴。
资料与方法
1.数据收集
本文数据来源于Lauer等[11]对COVID-19潜伏期分布估计的早期研究,该研究纳入2020-01-04至2020-02-24中国湖北以外确诊的181例COVID-19患者,这些患者的基本信息以及感染暴露和症状出现的时间区间均可从网络新闻或公共卫生报告中获取。
2.统计学方法
考虑包含n个独立样本的研究,假设样本i(i=1,2,…,n)感染暴露和出现症状的时间分别为Ei和Oi(Oi>Ei),则该样本的潜伏期为Ti=Oi-Ei。然而,在实践中我们往往只知道感染暴露或症状出现落在某个可能的区间,也就是说,我们一般获取如下形式的双区间删失观测(图1):

图1 潜伏期观测数据示意图
Xi={(EiL,EiR],(OiL,OiR]}
其中,Ei∈(EiL,EiR],Oi∈(OiL,OiR],而且,EiL≤EiR,OiL≤OiR;特别地,当区间的左端点与右端点相等时(EiL=EiR≜Ei或OiL=OiR≜Oi),表示观测到的是确切的感染暴露或症状出现时间。如果能够获取Ei或Oi确切的观测时间,则
Ti∈(OiL-Ei,OiR-Ei],Ti∈(Oi-EiR,Oi-EiL]或Ti=Oi-Ei。
我们关注的是潜伏期Ti的分布F(t),记S(t)=1-F(t)为Ti的生存函数。以下简述基于区间删失观测的潜伏期分布估计方法(表1)。

表1 潜伏期估计方法汇总
(1)单区间删失方法
假定所有样本的症状出现时间都是已知的,即对任意i,OiL=OiR≜Oi,此时,Ti∈(Oi-EiR,Oi-EiL]≜(TiL,TiR]。这样,潜伏期Ti的分布估计就简化为单个区间删失数据的分析。令{sj}mj=0为{0,TiL,TiR:i=1,2,…,n}的唯一有序排列;记αij=I(sj∈(TiL,TiR])(I是示性函数),pj=F(sj)-F(sj-1),则似然函数可以表示为:
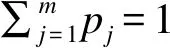
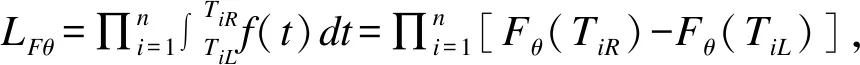
(2)双区间删失方法
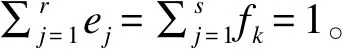
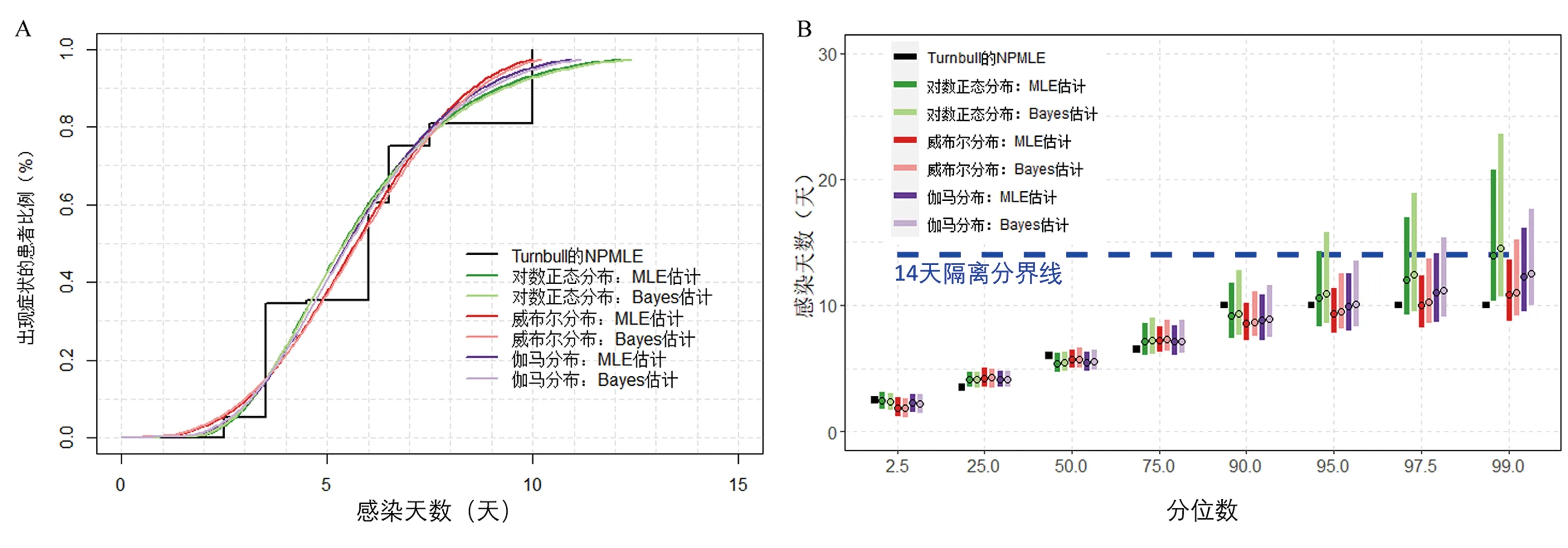
类似地,如果假定潜伏期Ti服从某种特定的分布且可以表示成上述线性模型的形式,则我们同样可以通过AFT模型来刻画潜伏期的分布。令δi=I(EiL 其中,gφ和fθ分别为感染暴露时间和潜伏期的概率密度函数,φ和θ分别为各自的分布参数。通常,假定感染暴露时间在观测区间(EiL,EiR]均匀分布,这样,我们最大化似然函数就可以获得潜伏期分布参数θ的MLE估计,从而得到潜伏期分布的估计。与单区间删失方法一样,我们也可以通过贝叶斯方法获得潜伏期的分布估计。 (3)随机过程方法 图2 COVID-19潜伏期估计的更新过程方法模型 对于最大似然估计,我们计算负对数似然函数值进行同类方法内的比较;同样计算贝叶斯估计的负对数似然函数值,并与最大似然估计进行比较。此外,我们对各种方法的数据利用情况及影响传染病防控政策制定的潜伏期分位数估计(2.5%、25%、50%、75%、90%、95%、97.5%和99%分位数)进行仔细比较。 本研究所有数据处理和建模过程均通过R软件实现。其中,单区间删失方法的NPMLE估计采用survival程序包,而MLE估计和Bayes估计采用icenReg程序包;双区间删失方法的NPMLE估计采用doubcens程序包,而MLE估计和Bayes估计采用coarseDataTools程序包;随机过程方法基于Qin等[12]提供的R代码实现。 研究数据来源于2020-01-04至2020-02-24中国湖北以外确诊的COVID-19患者,总共181例。这些患者来自以亚洲为主的五大洲;年龄跨度较大,从2岁到80岁,平均年龄为46.0(±15.4)岁;108例(61.0%)为男性;159例(90.9%)有武汉旅居史,137例(75.7%)有明确的症状出现日期。具体信息见表2。 表2 研究对象的基本特征[n(%)] 将137例具有明确症状出现日期的COVID-19患者纳入单区间删失方法分析。图3的结果显示,Turnbull的NPMLE存在较多的跳跃“阶梯”;对于参数模型,相同的分布假设下,MLE估计与Bayes估计结果相近;尽管各模型对COVID-19的中位潜伏期的估计接近(5.4~6.0天),但对于大分位数(如>95%分位数)的估计与Turnbull的NPMLE估计相比差别有变大趋势,置信区间变长,尤其是潜伏期的对数正态假设下,其MLE估计和Bayes估计与Turnbull的NPMLE估计差距最大,且99%分位数估计超过14天。 图3 COVID-19潜伏期分布的单区间删失方法分析 纳入所有181例数据的双区间删失方法分析结果见图4。可见,NPMLE估计存在较多的“跳跃”点;相同分布假设下的参数模型,其MLE估计与Bayes估计接近;相比之下,不同分布假设的参数模型估计的结果差别要大,估计的中位潜伏期在5.0~5.5天之间;对于潜伏期大分位数(如>95%分位数)的估计与NPMLE估计差距变大,95%置信区间变宽,在对数正态假设下尤为明显。这些结果都与单区间删失方法得到的结果类似。 图4 基于双区间删失数据的COVID-19潜伏期分布估计 从更新过程的角度,研究数据中包含59例2020-01-19至2020-01-21期间离开武汉并在武汉以外确诊且获得确切症状出现日期(即前向复发时间明确)的患者,得到COVID-19潜伏期分布的MLE估计(图5)。除威布尔分布假设下潜伏期分布的小于50%分位数估计明显偏离其他两种分布假设(对数正态分布和伽马分布)外,其他各分位数估计接近,而且潜伏期中位数估计在4.0天左右。 图5 基于更新过程的COVID-19潜伏期分布估计 为了进行模型间的比较,我们计算各模型拟合结果的负对数似然函数值。尽管Bayes估计目标函数的优化采用的是后验分布函数,但本研究的结果显示,相同分析方法和分布假设条件下,按潜伏期分布的Bayes估计计算得到的负对数似然函数值,略大于MLE估计的结果(表3),数值非常接近,提示Bayes估计与MLE估计吻合度很高。因此,这里仅比较不同模型的MLE估计。 表3 不同分布假设及分析方法获得的COVID-19潜伏期估计结果 本研究的结果显示,无论是单区间删失方法、双区间删失方法,还是随机过程的角度,各种方法不同分布假设条件下,其MLE估计的负对数似然函数值都非常接近,且都大于非参数方法。这提示,从拟合优度的角度,非参数方法的结果优于参数方法。如果我们以非参数模型结果为基准,无论是单区间删失方法还是双区间删失方法,对数正态分布假设条件下的潜伏期大分位数(≥95%)估计更倾向于偏离非参数模型;而随机过程方法在三个分布假设条件下的潜伏期大分位数估计基本一致。从数据利用的角度,由于受诸多假设条件的限制,随机过程方法能够利用的样本数目(n=59)明显少于单区间删失方法(n=137)和双区间删失方法(n=181)。 本研究首先回顾了COVID-19潜伏期分布的统计估计方法,即单区间删失方法,双区间删失方法和随机过程方法,从收集数据的结构、数学符号化过程到模型的构建和实现,以及模型的评价,逐一进行了详细介绍;其次,利用Lauer等[11]收集的181例确诊患者感染暴露和出现症状的信息,对三种方法的MLE估计和Bayes估计结果进行了比较。我们的比较结果显示,同类方法不同分布假设间,非参数方法要比参数方法拟合效果更好,但非参数方法存在较多的跳跃点,且无法获得估计的95%置信区间;同类方法相同分布假设条件下,MLE估计与Bayes估计结果和拟合效果相近;同类方法的对数正态假设条件下获得的潜伏期分布的大分位数(>90%分位数)可能较大地偏离非参数估计结果;从数据利用的角度,双区间删失方法对数据的利用率最高;由于数据收集和利用的差异,不同方法得到的潜伏期分布估计可能存在较大差异。 区间删失数据的NPMLE估计被认为是分析该类数据的金标准[7]。但非参数方法依赖于对潜伏期可能取值点的“猜测”,一般只能从样本数据获得,对于样本数据以外的取值点,在估计结果则体现为无信息的“水平线”或“线性插值”,这就是我们看到NPMLE存在较多“跳跃”点的原因(图1A和图3A)。另外,因为NPMLE估计不需要任何的分布假设条件,从而无法进行统计推断,也就没法计算估计的置信区间。基于此,研究人员普遍选择的是潜伏期分布的参数模型估计[6,9-13]。然而,由于我们难于像非删失数据估计方法那样方便地检查统计分布假设的准确性(如残差),我们完全有必要先获得区间删失数据的NPMLE,并将参数模型结果与之比较,只有在参数模型并未严重偏离NPMLE结果情况,才能有理由相信我们的参数模型结果的有效性和可靠性[16]。 在我们的研究里,同类方法相同分布假设条件下的MLE估计与Bayes估计结果和拟合效果相近。但是,一般模型的Bayes估计,通常以MLE估计为初始估计,采用模拟算法(如MCMC方法)通过最大化后验函数获得。前期关于COVID-19潜伏期分布估计,Backer等[10]和Linton等[6]利用stan语言[20]实现,而且一般需要额外计算留一法交叉验证(leave-one-out cross validation,LOO-CV)或泛化信息量准则(widely applicable information criterion,WAIC)参数[21]进行模型比较,模型的收敛性有时难以保证。因此,尽管Bayes估计有其优势[22],但无论是从理论还是计算的复杂度而言,基于区间删失数据的潜伏期分布Bayes估计不如其MLE估计直接和便捷。 不同分析方法之间,数据利用的效率差异较大,结果的变异也较大。显然,基于双区间删失方法利用了所有收集的181例数据,显示了最高的数据利用效率。理论上,双区间删失方法对单区间删失数据同样适用,为此,我们采用双区间删失方法对137例单区间删失数据重新进行了分析,结果与单区间删失方法完全一致。而Qin等[12]提出的随机过程方法,虽然最终分析计算过程比较简单,而且在一定程度上可纠正数据收集过程中的回忆偏倚,但其假设条件较多,导致满足条件的数据较少,从而产生样本选择偏倚,使其计算结果与区间删失方法得到的估计差别较大。另外,在新发传染病流行早期,数据采集和分析利用效率直接影响防控决策及其效果。因此,基于双区间删失数据分析方法是潜伏期的分布估计较好的选择。 综上所述,采用双区间删失数据的最大似然法估计传染病潜伏期分布,可以提高数据的收集、利用和分析效率,减少样本的选择偏倚;潜伏期分布估计过程中,除了比较不同分布假设下的估计结果,还要与非参数模型估计进行比较,并在不同数据集之间验证结果的可靠性;对潜伏期分布大分位数的估计和解释要谨慎,仅依赖于模型拟合优度统计量获得的“最佳”估计,有可能高估最长潜伏期。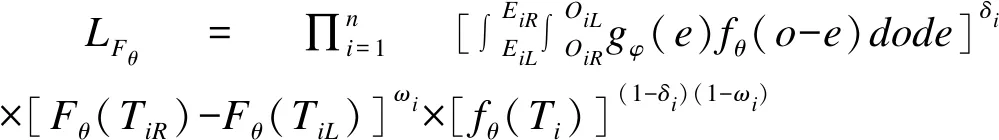
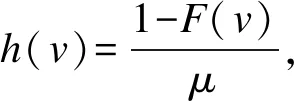

3. 模型评价
4. 统计软件
结 果
1. 基线特征

2. 潜伏期分布估计


3.模型评价

讨 论
