分形理论在矿物加工中的应用基础及研究进展

刘欣然 ，周伟光 ，谢广元 ，彭耀丽，梁 龙，李懿江

(1.中国矿业大学 煤炭加工与高效洁净利用教育部重点实验室,江苏 徐州 221116；2.中国矿业大学 化工学院,江苏 徐州 221116)

矿产资源是国民经济和社会发展的物质基础，矿物加工技术是矿产资源高效提取利用的技术基础。近年来，随着矿产资源的开采、开发，我国矿产资源禀赋逐渐变差，矿物加工理论和工艺技术的升级与创新成为保障矿产资源绿色高效获取的现实需求。鉴于此，学者们借鉴其他学科研究技术，通过多学科交叉、融合的方式开展研究，以期实现矿物加工过程环节优化及综合指标提升。其中，分形理论因具有包容性强、运行方式灵活、应用范围广等特点，为矿物加工过程部分基础问题的解决提供了良好的思路和借鉴。

分形理论是一门非线性学科，具有自相似性等基本特征，可用于描述自然界中各类非规则现象。发展之初，分形理论研究对象主要涉及河流道路轨迹及高分子链空间结构等，后逐渐应用于水处理领域，以表征悬浊液中絮体结构特性[1]。需要说明的是，矿物加工领域同样涉及众多非规则现象，分形理论的应用亦有助于解耦相关过程、阐明其机理。目前，矿物加工领域涉及分形理论的研究方向主要有：基于自然界矿石中有用矿物的分形分布规律，预测矿石机械拣选技术指标和经济效益[2]；基于不同碎磨条件下矿石的粒度分形分布规律及形状分形特征，优化工艺参数，研发新型破碎磨矿设备[3]；基于不同外界条件下矿浆悬浊液中絮体结构的分形特征，研究颗粒聚集/分散行为，提升浮选综合指标，调控絮体沉降速率[4]；基于不同过滤条件下滤饼孔隙结构的分形特征，探索提高过滤效率的方法[5]等。

另一方面，与其他应用领域相比，分形理论在矿物加工中的应用仍处于发展阶段，相关研究工作较少且不够深入，大部分相关研究成果尚未投入实际生产。考虑到分形理论广阔的潜在应用前景(尤其是选矿过程智能化和高效化发展方向)，有必要对前人研究成果进行总结、归纳，并在此基础上理清、拓宽研究思路，明确未来研究方向。其中，在矿石拣选、矿石碎磨以及过滤(高浓度矿浆经过滤机加压形成滤饼)过程中，分形研究对象为矿石碎块、粒度较大的矿石颗粒以及含水量相对较低的滤饼，且各工艺环节通常处于干燥或矿浆浓度相对较高的环境中，一般不涉及微细矿物颗粒的混凝；在调浆、矿物浮选、沉降(包括过滤操作前矿浆悬浊液中矿物颗粒絮体沉降阶段)过程中，分形研究对象为微细矿物颗粒及由微细矿物颗粒形成的絮体，且各工艺环节操作均处于液相环境中，涉及微细矿物颗粒的聚集/分散以及复杂混凝过程。因此，笔者将矿物加工过程中涉及分形现象的工艺环节分为“矿石拣选、碎磨及过滤”、“调浆-浮选与絮体沉降”2 部分，并分别对其中的分形现象进行分析，拟对分形理论在矿物加工领域的研究做出全面综述。

笔者在概述分形理论相关概念基础上，针对部分具有自相似性等分形特征的矿物加工工艺环节(包括矿石拣选、矿石碎磨、调浆、矿物浮选、沉降、过滤等)，归纳总结分形理论在以上工艺环节中的研究现状，并基于各研究现状分析、展望分形理论在矿物加工领域的发展方向，旨在基于多学科交叉以实现矿物加工学科的深入和可持续发展,为剖析某些复杂过程提供方法支持和技术借鉴。

1 分形理论

MANDELBROT 于1975 年提出了分形理论概念[1]，认为分形体具有自相似性(局部为整体的缩影)、无标度性及自放射性三大基本特征，这不仅表现在事物的图形外观上，还可体现在能量、时空、性质等方面。分形现象在自然界中普遍存在(图1)，并广泛应用于众多学科的基础研究。

图1 常见分形现象Fig.1 Common fractal phenomena

欧氏几何中维数仅能用整数表示，而对于复杂且不规则的分形体则需采用分形维数概念。分形维数是分形的度量指标，被用于描述分形体不规则程度及其在空间中的填充程度，可与诸多自然特性相关联，具有极高的包容性。通常，二维分形维数适用于描述平面图形几何轮廓性质；三维分形维数能够揭示分形体三维空间几何特性；若颗粒群粒度分布具有分形特征，则可通过分布分形维数表征[3]。

依据研究对象特性差异，研究者提出了不同的分形维数定义方法，其中最常用的方法为相似维数。相似维数的本质是把研究对象看作一个可被划分为N(F,r)个子集的集合F，每个子集以相似比r与原集合相似，如果存在一个数Df，使得当r→0 时有

则称Df为研究对象的相似维数，即分形维数。该定义方法计算简单、高效，广泛适用于各类具有自相似性质的研究对象，但仅能对研究对象作整体性描述，无法精确描述其局部分维特性[1]。

分形维数计算过程模型如图2 所示。矿物加工领域存在诸多分形现象，该模型能广泛匹配各类分形现象的分形维数求解过程。例如，通过计算矿石中有用矿物分布分形维数，可揭示其中有用矿物分布规律[6]；通过计算碎磨过程中矿石粒度分布分形维数，可揭示不同碎磨条件下矿石粒度变化规律[7]；通过分析矿浆混凝过程中矿物颗粒絮体分形维数，可反映不同变量条件下絮体结构及颗粒动态变化规律等[8]。

图2 分形维数计算过程模型Fig.2 Fractal dimension calculation process model

2 分形理论在矿石拣选、碎磨及过滤中的应用

2.1 分形理论在矿石拣选中的应用

现代矿石拣选过程通常利用传感器，基于有用矿物与脉石矿物元素种类及含量等性质差异实现2 者的分离。拣选工艺主要包括矿块拣选和矿石批量拣选2 种类型，其基本流程包括给料、传感器检测、信号处理以及物料分离4 个部分[9]。拣选工艺在矿石采选领域有广阔的应用前景，但原有矿石批量拣选技术存在试样矿物分布规律缺乏代表性、预期拣选技术指标与实际拣选效果差异大等缺陷，影响应用可行性。

自然成矿过程具有自相似性(图3)[10]，矿石品位与质量存在分形关系(式(2))[6]，通常采用人工检测的方法获取矿石样品的品位和质量数据，再通过分形维数定义计算矿物在矿石中的分布分形维数。

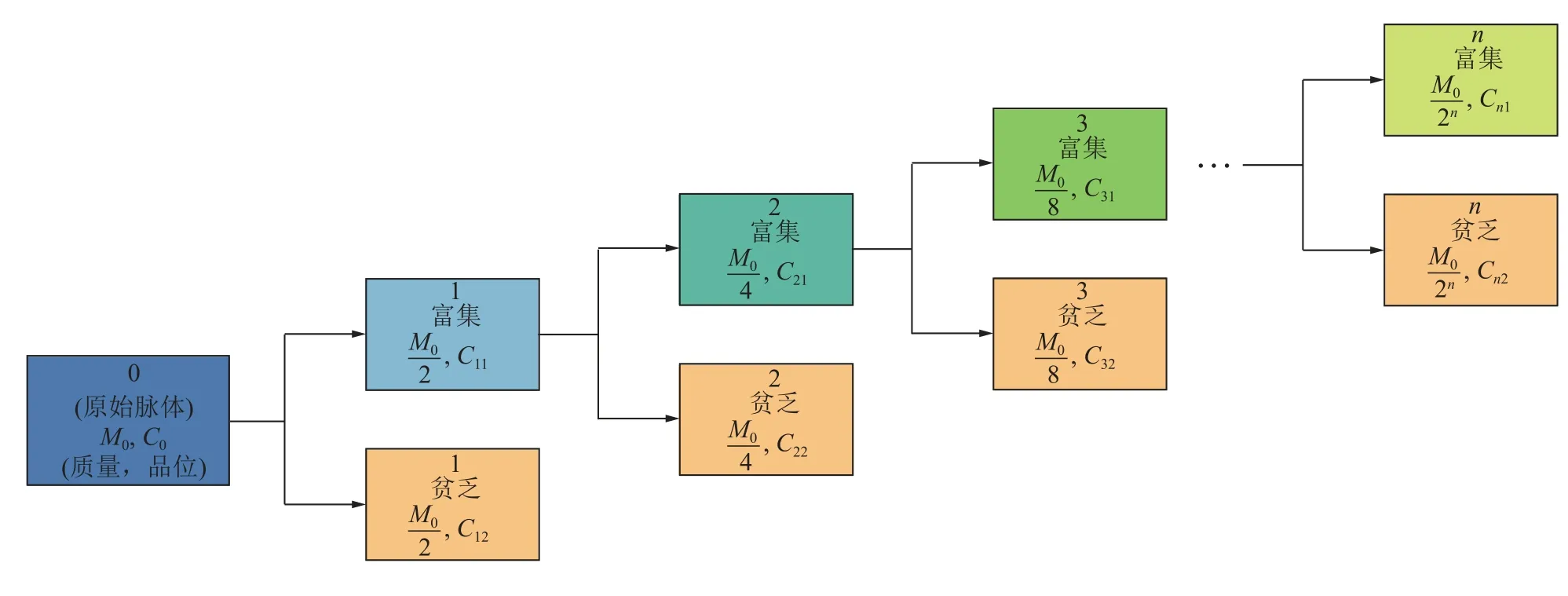
图3 具有分形特征的成矿模型Fig.3 Metallogenic model with fractal characteristics

式中，C(M)为富集部分矿石品位；M为富集部分矿石质量；Dr为矿物在矿石中的分布分形维数，Dr越大，矿物分布越不均匀。

LI 等[2]发现将分形规律引入矿石批量拣选领域，并开展以下研究：首先，基于不同矿体中矿物分布规律的分形结构特性差异，在原有研究基础上提出矿石批量拣选(BOS)模型(式(3))，并根据BOS 模型，建立矿石批量拣选技术指标(如给矿品位、精矿品位、精矿产率和金属回收率)及经济效益指标的预测模型。

式中，c为品位阈值；m为高于品位阈值累积矿石质量分数；G为分形量度，G越大，矿物越分布在较高品位下，可由对矿石样品的品位和质量数据分析得到。

LI 等[11]以不同地区的3 种铜矿样品为研究对象，对模型的准确性进行验证，整体上准确度较高。总体而言，将分形理论引入矿石拣选过程建模中，可通过矿石性质有效预测拣选效果。虽然该研究仍停留在理论层面，尚未应用于实际生产，其后续深入研究却对推动矿石批量拣选工业的快速发展大有裨益。

2.2 分形理论在矿石碎磨中的应用

矿石碎磨过程中，单一矿石的每次碎裂都将分裂成更小的矿石颗粒，矿石碎裂具有自相似性(图4)[12]，因此该过程中矿石的粒度、形状和能量消耗等性质变化均具有分形特征。

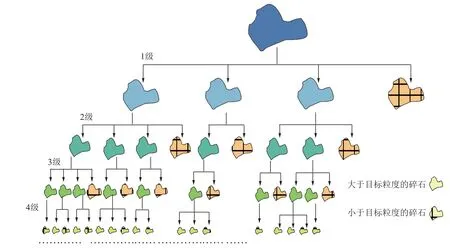
图4 具有分形特征的矿石颗粒破碎模型Fig.4 Fractal model of ore particle crushing

2.2.1颗粒粒度分布分形规律

颗粒粒度是矿石碎磨过程中最重要的性能评价指标，其分布存在分形特征(式(4))[13]。通常采用粒度分布法研究矿石颗粒粒度分布分形维数，较为常见的粒度检测方法有筛析法、沉降法和激光粒度测定法等：对于粒度较大的矿石颗粒，多采用筛析法；对于微细粒粉体，多采用激光粒度测定法。

其中，d为颗粒粒度；n为系统颗粒总数；Yn(d)为粒度小于d的颗粒数；Dg为粒度分布分形维数。Dg越大，细粒级所占比例越高，颗粒分布越不均匀，且颗粒表面越粗糙。当Dg接近2 时，矿石主要发生表面磨损；当Dg接近3 时，矿石主要发生整体碎裂[7]。

研究表明，矿石碎磨过程中颗粒粒度分布分形规律与碎磨工艺参数有着密切的关联。例如，高锋等[12]破碎磁铁矿时发现，随着破碎级数增加，矿石粒度分布分形维数逐渐增大，增大速率则逐渐减小并最终趋于稳定。ZHANG 和YANG 等[14-15]研究矸石和低阶煤粉碎时发现，矿石粒度分布分形维数随粉碎压力(能量输入)的增大呈先增大后趋于稳定的趋势。杨志远等[16]利用行星磨制备超细煤粉时发现，通过改变磨矿时间、添加助磨剂、优化球配比等调节颗粒粒度分布分形维数，能够实现矿物磨矿过程及磨矿效率的有效控制。可见，基于颗粒粒度变化的分形特征研究，有助于实现对矿石碎磨工艺的过程优化与智能控制。

2.2.2颗粒形状、碎磨能耗分形规律

矿石碎磨过程中，随着颗粒不规则程度的增加，仅通过粒度分布评价矿石碎磨性能存在一定的局限性，于是研究者提出采用颗粒质量(三维)、投影面积(二维)、表面积分形维数描述颗粒特性。其中，质量分形维数采用质量-粒径法计算(式(5))，投影面积、表面积分形维数则分别通过图像分析法测量，即通过光学显微镜、透射电镜或扫描电镜拍摄颗粒图像，随后利用Image J 等图像分析软件测量颗粒投影面积和边界长度，进而计算分形维数(式(6)、(7))[17]。

其中，M(d)为颗粒质量；A(L)为颗粒投影面积；L为投影特征长度；γ为码尺长度；P(γ)为投影周长；Dm为质量分形维数；Da为面积分形维数；Dp为边界分形维数。表面积分形维数Ds=Dp+1，Ds越大，颗粒表面越不光滑。

颗粒形状分形维数不仅取决于碎磨工艺参数，还可与其他特征参数相联系。焦红蕾等[18]研究煤炭粉磨过程时发现，颗粒表面积和质量分形维数可用于磨矿能耗和产品成浆浓度的计算，并通过过程调控实现了磨机工作效率的提升。WANG 等[19]建立了矿石破碎中比表面积及裂纹面积的分形模型，进而推导出矿石材料的表面能计算方程，为破碎方法的选取及破碎过程的能量控制提供了理论基础。胡松等[20]发现煤块在单轴压力载荷下，随着应力增加，煤表面分形维数呈先缓慢增大后急剧增大的非线性关系，从微观层面解释了煤表面结构在不同应力应变下的变化规律。

矿石颗粒的碎裂通常是逐级变化的，其中每级破碎都伴随着能量的消耗。目前，如何节能降耗仍是矿石碎磨领域的核心问题，对此部分研究者进行了碎磨过程能耗模型的探索。胡振中等[21]发现，传统Bond能耗公式虽能较准确预测辊式破碎机和锤式破碎机在煤破碎过程中的能耗规律，但对颗粒入料及产物的细度模数有较高要求，随后新建了基于能耗分形维数的能耗公式，经检验发现其对细度模数的选取要求不高，且能耗预测值与实际值拟合程度更高，可有效解决原煤破碎能耗预测难的问题。蔡改贫等[22]基于分形理论通过构建破碎能耗、矿石粒度分布、设备结构参数、破碎工作参数间耦合关联，建立了低频振动挤压破碎能耗预测模型，其预测值与实际值拟合较好，可应用于新型板辊式低频振动破碎机的研发，以计算矿石破碎所需要能量，从而选择最优工作参数。

目前，矿石碎磨领域分形规律的部分研究成果已应用于实际生产，但多数研究仍停留在对分形维数与碎磨生产工艺参数间的定性分析方面，定量关系的相关研究较少，因此该领域仍有较大的研究、探索空间。总体而言，矿石颗粒形状及碎磨能耗分形规律的研究有助于进一步优化生产工艺参数，其相关成果对未来工程应用亦具有重要指导意义。

2.3 分形理论在过滤中的应用

过滤是固液分离过程的重要环节，其操作过程可分为2 个阶段：第1 个阶段是过滤操作前矿浆悬浊液中矿物颗粒絮体沉降阶段，第2 个阶段是高浓度矿浆经过滤机加压形成滤饼阶段。在第2 个阶段，除矿浆性质外，滤饼性质也可影响最终过滤效果。滤饼孔隙在平面的投影可看作是形状不规则的多边形。因此，可采用图像分析法测量滤饼截面孔隙周长和面积，计算分形维数表征孔隙边界复杂程度[23]。

式中，P(A)为滤饼截面孔隙周长；A为滤饼截面孔隙面积；D′p为滤饼截面孔隙分形维数，D′p越大，孔隙形状越不规则，过滤效果越差。

滤饼分形结构与宏观过滤行为密切相关，基于滤饼分形结构特性的调节有助于实现改善宏观过滤效果的目标。来庆腾[24]发现，煤泥滤饼的上层孔隙率大、平均孔径小、分形维数大，而下层滤饼孔隙率小、平均孔径大、分形维数小，助滤剂的添加可针对性降低滤饼某些位置的分形维数，增大孔隙率，从而提高过滤效率。陈茹霞[25]研究颗粒性质对煤浆过滤效果的影响时发现，煤颗粒粒度越小，滤饼的分形维数越大，而颗粒粒度不均匀时，滤饼的分形维数从底层到表面逐渐增大，并由此提出为实现较好的过滤效果，应严格控制物料粒度组成并优化滤饼上层结构的思路。

综上，探索不同条件下滤饼孔隙分形结构的变化规律，建立过滤操作与滤饼微观分形结构之间的关系，有助于从微观本质上解释固液分离机理、实现矿物宏观过滤行为的精准调控，并为难滤矿物过滤脱水设备的开发提供理论指导。

3 分形理论在调浆-浮选与絮体沉降中应用

调浆是浮选作业前的预处理作业，浮选是使目的矿物与脉石矿物分离的有效方法；沉降是过滤操作前的必要环节。在矿浆悬浊液体系中，微细矿物颗粒通过混凝的方式聚集形成絮体。若不考虑絮体的破碎情况，混凝过程可看作是微小颗粒结合成为小絮体，小絮体结合成大絮体，大絮体再聚集形成大絮团的过程，这在一定程度上满足自相似性和标度不变性的分形特征(图5)[26]。实践表明，絮体分形维数相关研究有助于充分揭示矿浆混凝过程机理，对指导矿物加工工程实践具有重大现实意义。

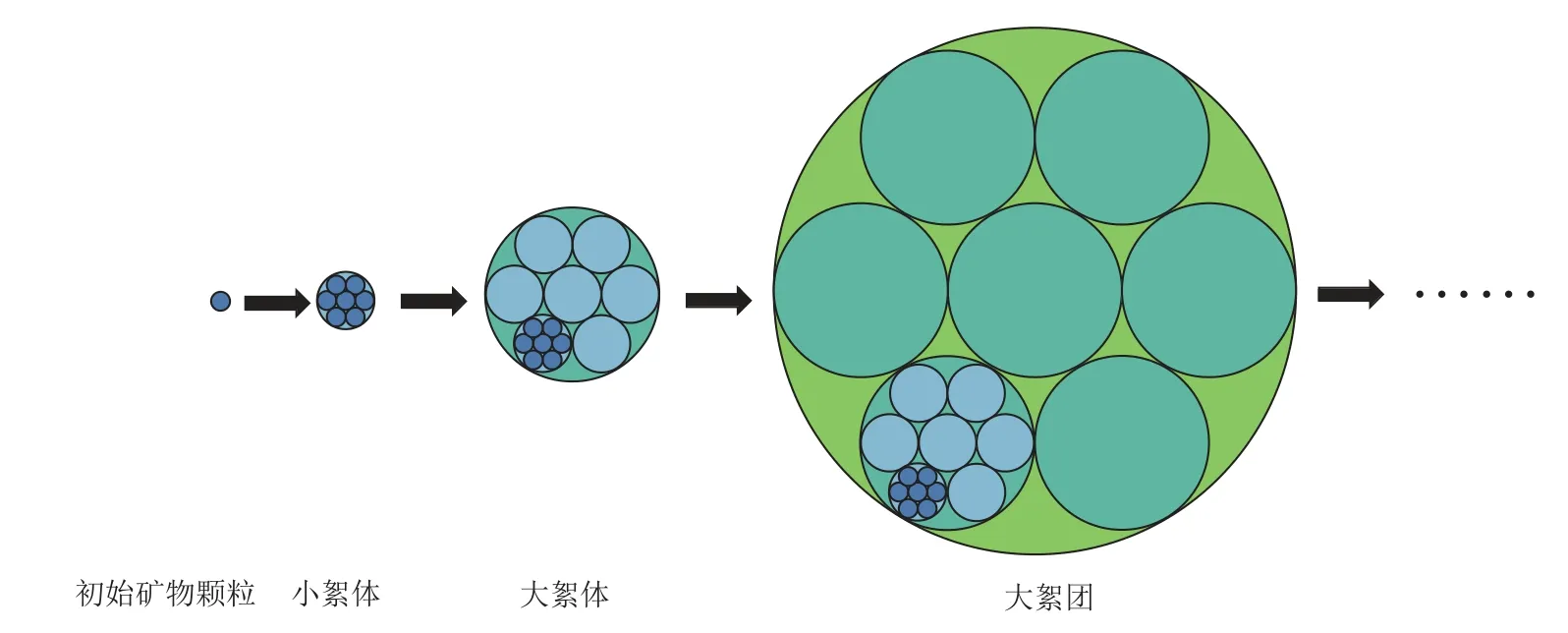
图5 具有分形特征的絮体生长过程模型Fig.5 Floc growth process model with fractal characteristics

3.1 矿物颗粒絮体分形维数测量方法

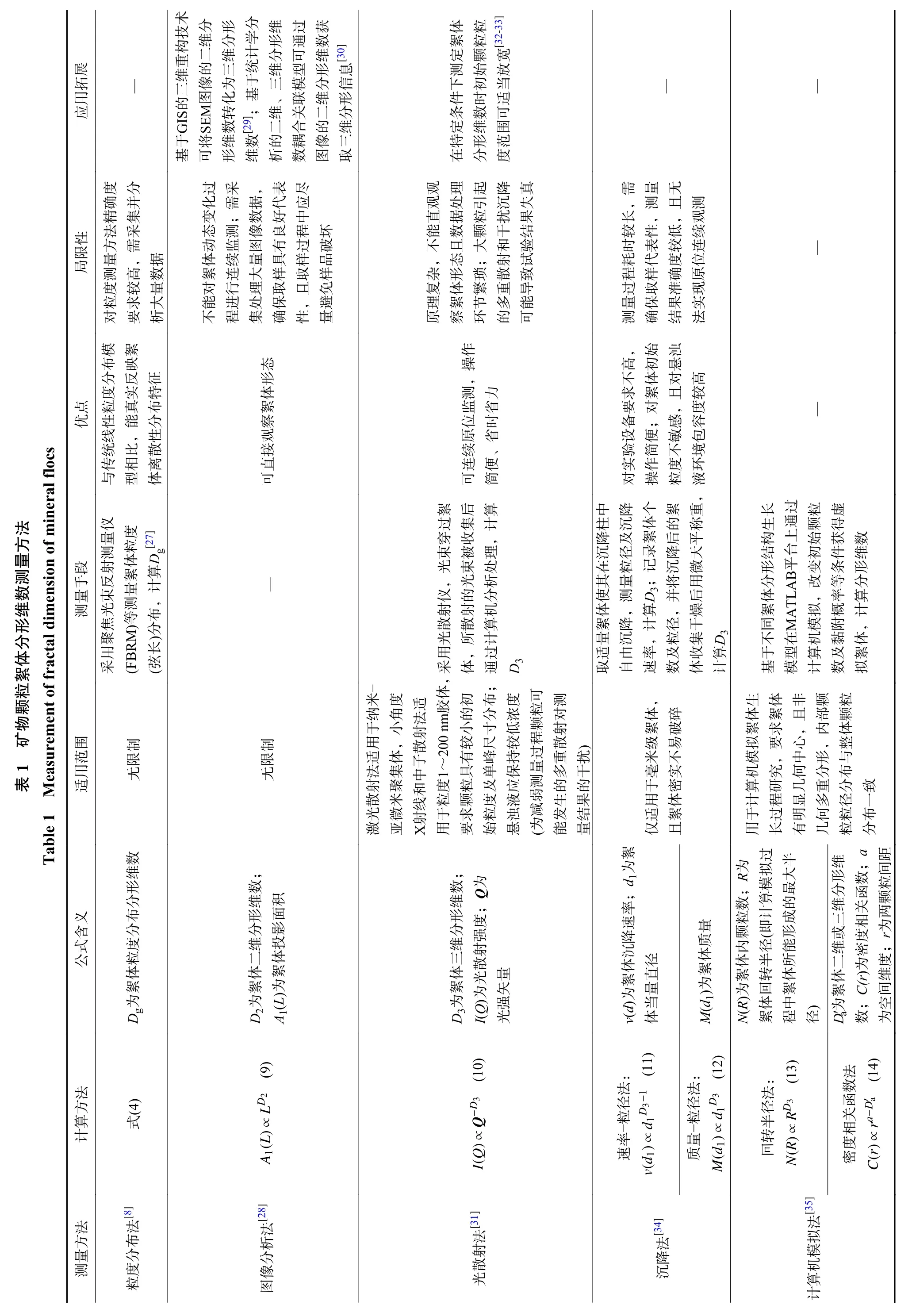
絮体粒度分布分形维数可准确反映絮体群粒度分布，二维和三维分形维数可反映絮体结构密实程度。根据矿浆环境及絮体性质差异，学者们设计了不同分形维数测量方法。表1 为矿物加工领域常见絮体分形维数测量方法及其适用范围和优缺点。由于不同测量方法的机理不同，分形维数差异可能较大，故对于同一体系内絮体间分维特性的表征宜统一测量手段。

3.2 基于分形理论的矿浆混凝行为

基于分形理论的混凝行为研究兴起于水处理领域。由于矿浆悬浊液与废水悬浊液某些性质相近，通常借鉴分形理论在水处理领域中涉及的部分研究方法与结论开展矿物加工领域矿浆悬浊液性质研究。

3.2.1典型混凝机理下絮体的分维特性

悬浮浆料体系中，多数微细颗粒可通过混凝的方式聚集，形成尺寸较大、结构较为复杂的絮体。凝聚和絮凝是混凝的2 种主要作用形式，压缩双电层、电中和、网捕卷扫、吸附架桥等是诱导混凝发生的基本作用机制。表2 为不同种类悬浊液在典型混凝机制下形成絮体的分维信息。相较于压缩双电层/电中和诱导形成的絮体，网捕卷扫作用下颗粒易被药剂水解产物包裹，使形成的絮体空隙较少、结构密实，从而絮体三维分形维数较大；而吸附架桥作用下形成的絮体分支多，结构更加开放，其三维分形维数最小。网捕卷扫、吸附架桥作用下形成的絮体普遍具有网链状结构，故对应二维分形维数通常较电中和诱导机制下絮体二维分形维数更小。

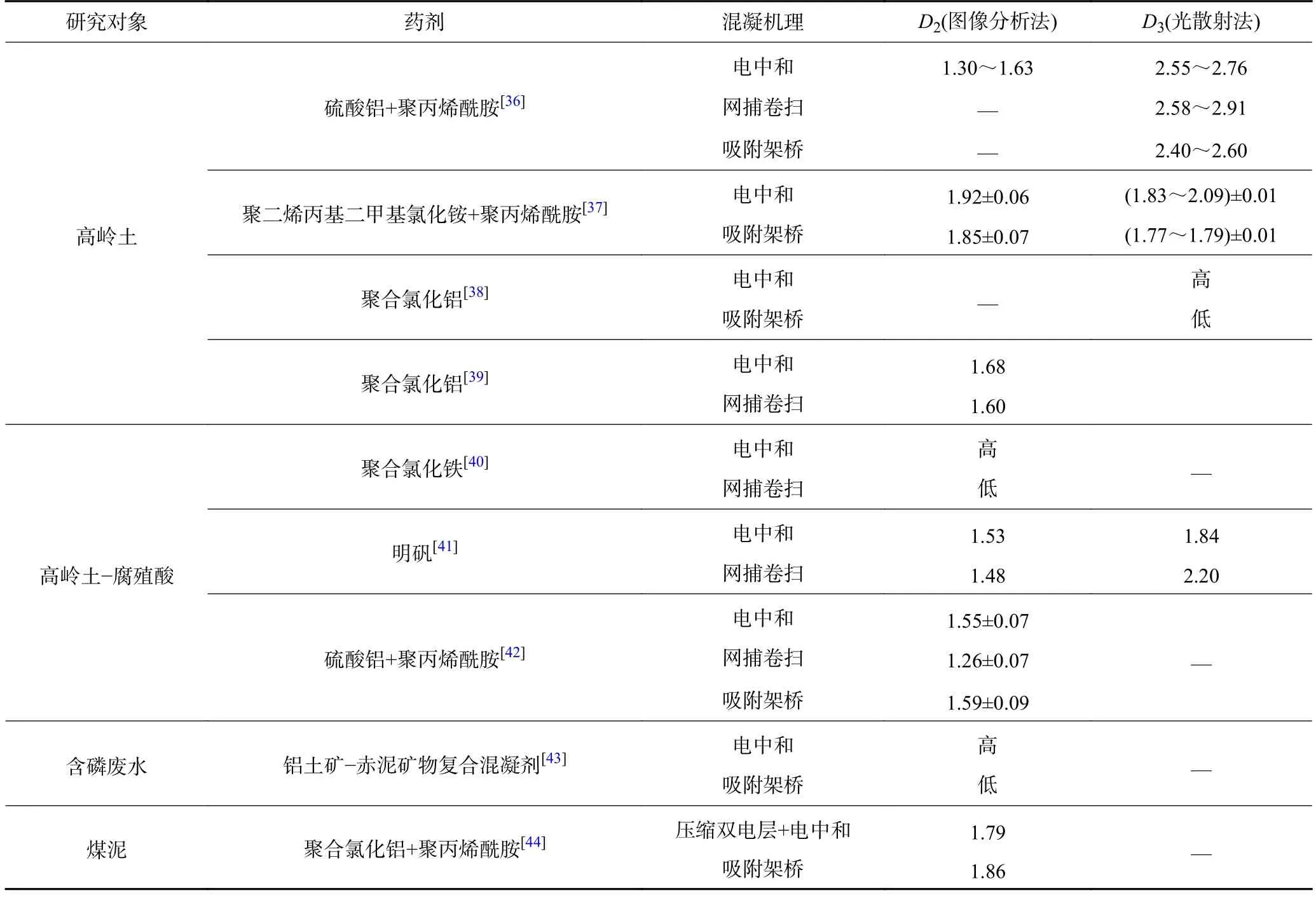
表2 典型混凝机理下絮体分维特性Table 2 Fractal dimension characteristics of flocs under typical coagulation mechanism

3.2.2分形理论在混凝动力学中的应用

随着矿浆混凝研究的深入，絮体形成、生长及其结构动态变化的规律愈发引人关注。由于分形理论广泛的适用性及其对絮体结构表征的直观性，越来越多学者尝试将分形理论引入颗粒混凝动力学研究过程中，以期更加深刻地揭示混凝过程中絮体空间结构及物理性质的转变规律。

(1)絮体分形结构生长模型。为探究絮体生长过程对混凝工艺的影响，研究者们提出了3 类反映絮体生长特征的分形结构模型(每种模型包含单体凝聚和集团凝聚2 个亚类)。表3 为不同分形结构模型下絮体分形维数和结构特点。虽然不同凝聚类型下的絮体性质各异，但其分形维数间存在着一般规律：由于单颗粒比微絮体更易进入到絮体的内部，并使絮体密实度增加，故单体凝聚比集团凝聚形成的絮体具有更高的分形维数；由于各种模拟方法假设的黏结概率不同，反应控制模型考虑了颗粒间的相互作用，为了克服颗粒或微絮体间的斥力，需要更高的碰撞频率才能形成絮体，故反应控制诱导的絮体分形维数区间较扩散控制诱导的絮体分形维更大。

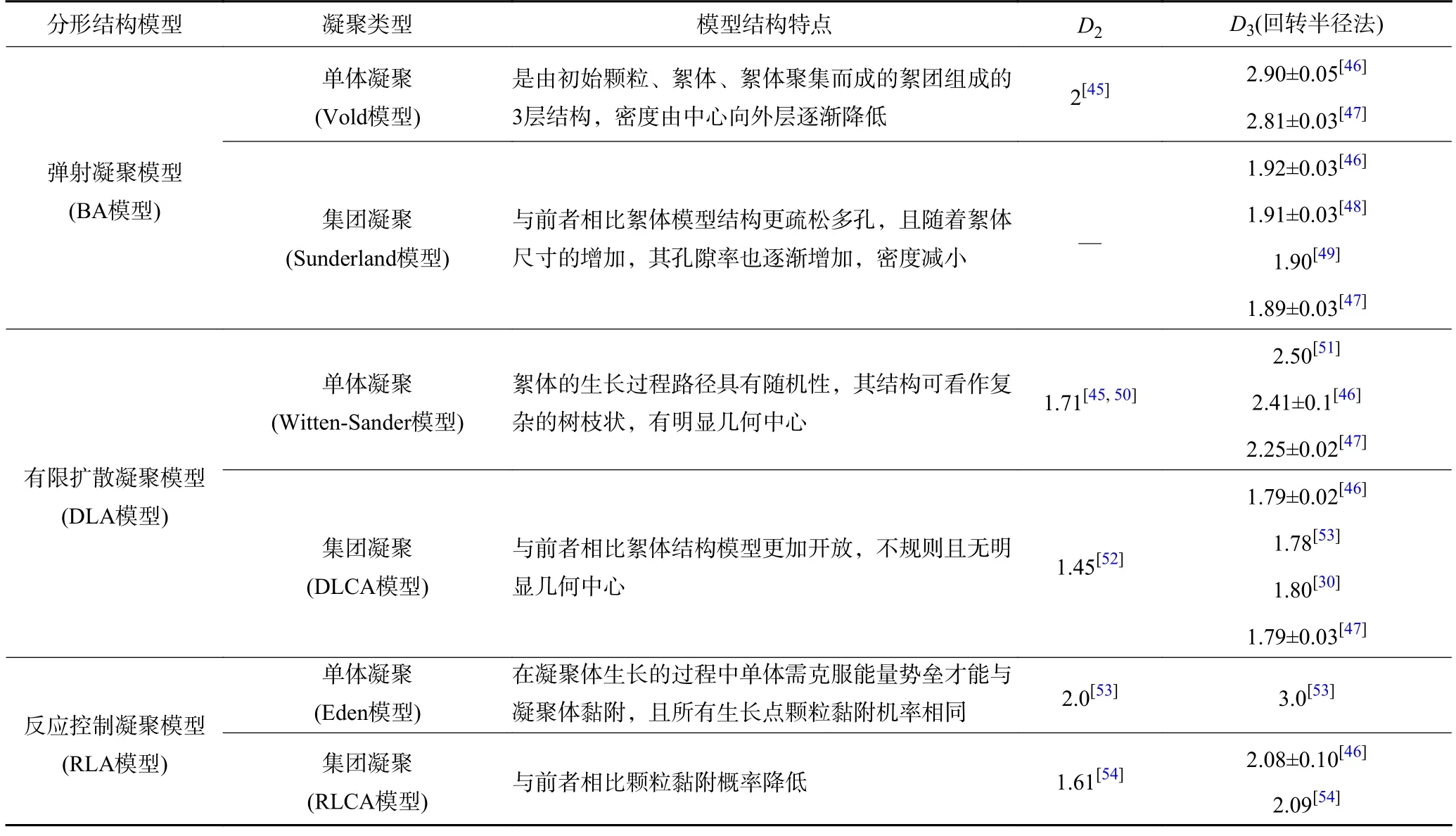
表3 不同分形结构模型模拟形成的絮体分形维数及其特点Table 3 Fractal dimension and characteristics of flocs simulated by different fractal structure models

(2)基于分形理论的混凝动力学模型。混凝动力学模型旨在通过数学建模揭示混凝过程中颗粒性质随时间动态变化规律，较为经典的有Smoluchowski 模型、群体平衡模型(PBM)等。通常情况下，流体中颗粒间碰撞机制主要有3 种：由分子热运动引起的布朗运动、由水力和机械搅拌引起的流体剪切以及由颗粒尺寸和密度不同引起的差速沉降等，这3 种机制所形成的混凝模式均可影响颗粒碰撞函数β。传统混凝动力学模型中综合碰撞函数的计算仅是3 种碰撞函数间的加和，并没有考虑3 者间潜在关联性。而实际混凝过程中，絮体重组会使絮体粒径、分形维数等性质发生变化，进而引起3 种碰撞函数及综合碰撞函数的交互改变。将絮体分形维数引入颗粒碰撞函数β，即可得到分形理论耦合的混凝动力学模型[55-56]。表4对比了2 种经典混凝动力学模型引入分形维数前后的差异。混凝动力学研究过程中分形理论的引入能够有效弥补传统混凝动力学模型的不足(如忽略颗粒形状、孔隙结构、不考虑絮体破碎重组等)，有助于深化对各操作变量引起的颗粒絮凝行为变化的内在机理的认识，对解耦颗粒混凝过程具有重大的理论意义。

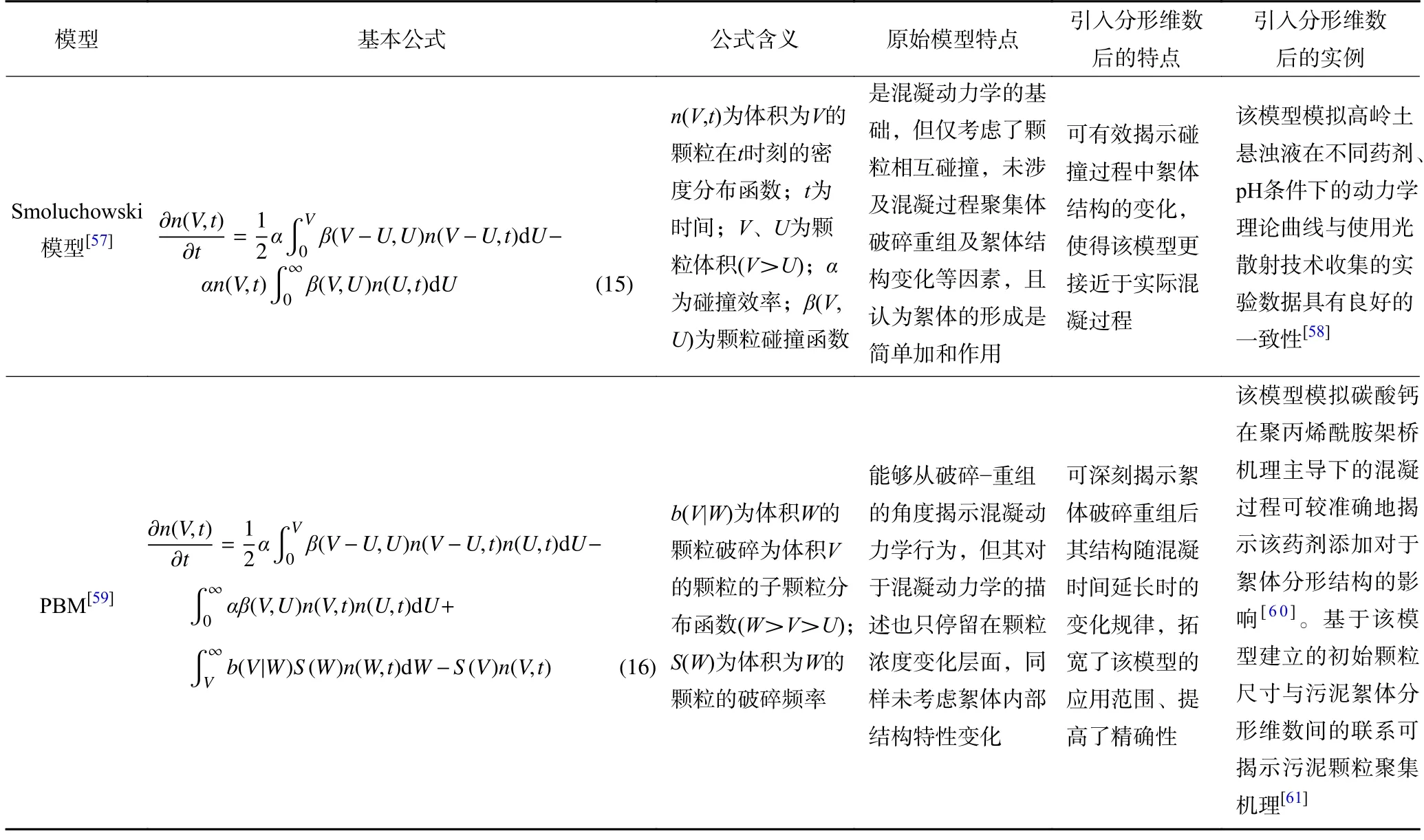
表4 分形理论的引入对两种经典混凝动力学模型的影响Table 4 Influence of fractal theory on two classical coagulation kinetic models

矿物加工调浆-浮选、沉降过程中，因作业目标差异，不同环节理想絮体结构也存在差异，如在尾矿沉降环节，为加强固液分离效率，理想絮体应粒度适宜，并具有一定抗剪切破坏能力；在浮选预调浆阶段，为使目的矿物与脉石矿物充分分散并选择性聚集，脉石矿物絮体强度应小于目的矿物絮体强度等。絮体其他结构特性与分形维数紧密相关，因此建立絮体不同结构参数之间的关系对矿物加工不同环节过程调控及指标优化具有现实意义。

(1)絮体密度。不同于单一颗粒，絮体内部往往存在大量空隙，在矿浆环境中空隙被液体占据而使絮体表观密度降低。对于分形维数与絮体密度(孔隙率)之间的函数关系，一般认为絮体密度、粒径与其分形维数满足：

其中，ρe为絮体有效密度(在水中的密度)；dp为粒径；D3=2.2～1.7[62]。故一般认为，絮体孔隙率越大，其密度越小，结构越松散，分形维数也越小。

(2)絮体粒度。絮体粒度与其分形维数间的关系可从单个絮体和絮体群2 方面分析。对于单一絮体，普遍认为絮体越大，其内部包含基本粒子数越多，对应分形维数越小[63]。对于絮体群，CHELLAM 等[64]研究不同分形维数絮体的粒度分布曲线时发现：当Df=3 时，絮体粒度分布范围较窄，但随着分形维数的降低，絮体粒度分布逐渐变宽且平均粒度向增加的方向移动。故一般认为，絮体粒度分布分形维数和平均粒径呈负相关，且当粒级范围相同时，细粒级所占比例越大，对应粒度分布分形维数越大。

(3)絮体强度。絮体强度是其抗破坏能力的表征，其大小取决于组成絮体颗粒间结合键强弱、数量以及絮体大小、密实度等性质。实际上，针对絮体强度与絮体分维特性间关联关系，YANG 等[65]将絮体视为黏性较高的流体，把强度、分形维数与非牛顿流体的宾汉切应力结合建立了关系式，最终得出了絮体分形维数越高，体系的宾汉切应力越大，絮体强度越大的结论。总之，分形维数越大的絮体，其内部结构越致密，组成絮体的颗粒间排斥作用越小，其强度也越高。

3.3 影响矿物颗粒絮体分维特性的因素

3.3.1药 剂

化学药剂被广泛应用于矿物加工过程不同工艺环节。考虑到絮体性质与矿物颗粒的聚集/分散状态紧密相关，因此常见的影响颗粒聚集/分散状态的药剂，包括捕收剂、分散剂和混凝剂等，是相关研究的重点。其中，浮选捕收剂、部分混凝剂能够通过强化矿物颗粒疏水，诱导颗粒通过聚团的形式形成具有不同分维特性的絮体。分散剂则能够通过增强矿物颗粒间排斥作用或空间位阻效应，实现不同矿物颗粒间的分散(絮体的破坏)[66]。表5 为常见药剂作用下不同种类絮体的形成机理及其分维特性。一般而言，单一电解质如AlCl3、CaCl2等主要诱导颗粒间发生压缩双电层作用，絮体分形维数随药剂用量的变化不明显；有机高分子混凝剂主要诱导颗粒发生吸附架桥作用，其超过一定用量后易导致絮体分形维数降低；无机混凝剂的作用机理最复杂，其用量较低时颗粒间主要发生电中和作用，而当其浓度较高时可发生网捕和架桥作用。

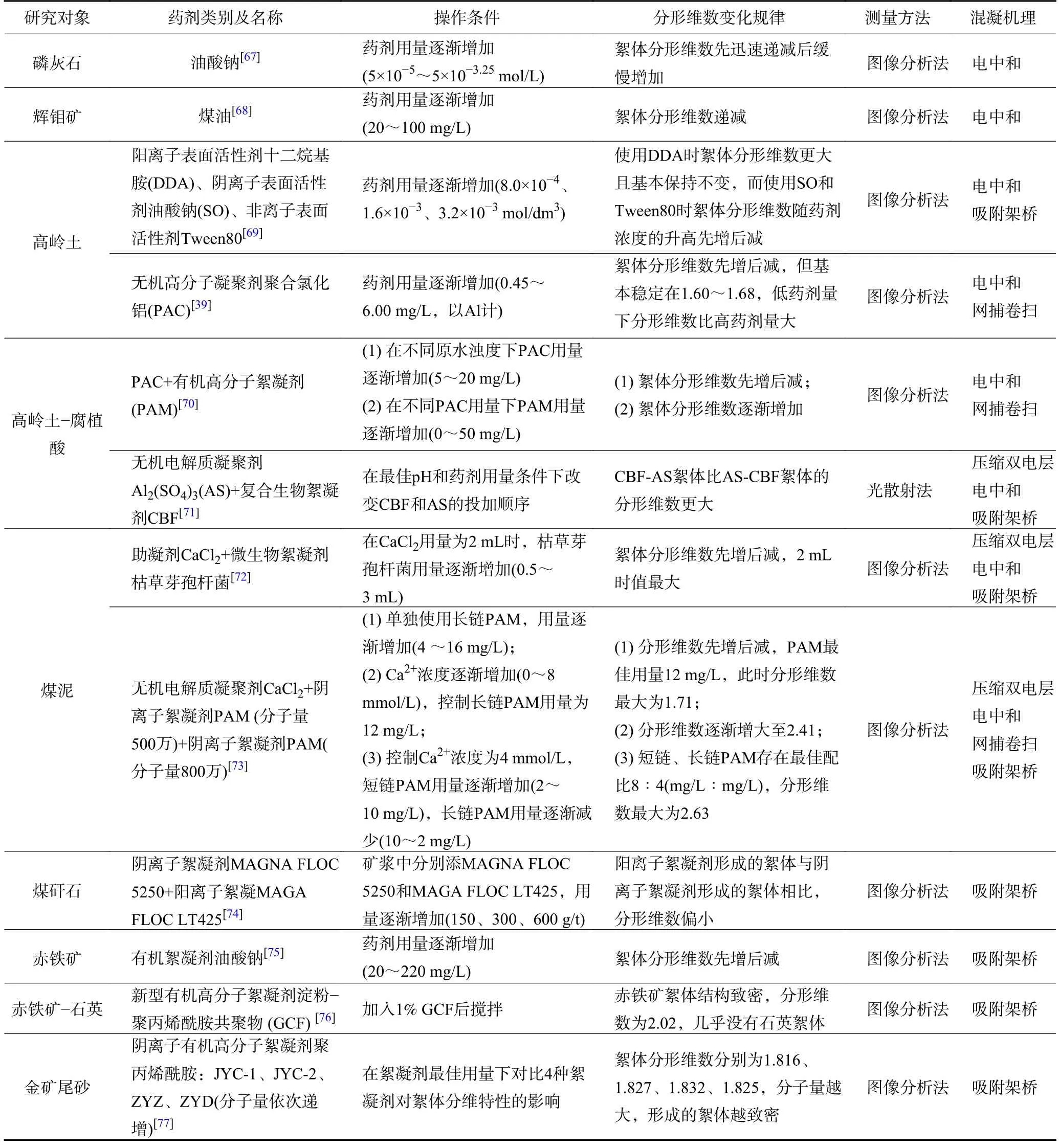
表5 药剂添加对矿物颗粒絮体分形维数的影响Table 5 Effect of chemical addition on fractal dimension of mineral particle flocs

3.3.2矿浆性质

矿浆性质包括环境pH、温度、盐离子等因素均能够通过影响颗粒聚集/分散状态改变絮体分维特性。

缓冲溶液的pH是影响化学反应的主要因素之一，pH过高或者过低，都会对化学反应产生影响，很多反应，尤其是一些生化反应，往往需要在一定的pH下反应才能正常发生，比如在特定细菌的培养以及生物体内酶促反应等等，都需要稳定的pH,pH变化幅度过大就会造成细菌死亡，无法正常繁殖，也会使得酶的活性丧失，难以发挥其促使相关反应的作用，因此实验室中经常需要配制一定浓度和一定pH的缓冲溶液，缓冲溶液的配制过程就涉及到缓冲对量取多少的问题，这就需要运用缓冲公式进行具体的分析。

(1) pH。矿浆pH 能够通过影响矿浆中矿物颗粒表面电荷分布，进而影响颗粒聚集/分散行为，导致形成的絮体分维性质改变。对于某些pH 敏感型混凝剂，不同pH 条件下其水解产物不同，最终的混凝效果及絮体分维性质也存在差异。例如，温海龙等[78]采用聚合氯化铝处理高岭土模拟废水时发现，pH 约为6.5 时絮体分形维数最大，这是由于此时铝离子水解的众多产物中聚十三铝(Al13)的含量最高，而Al13稳定性好且电荷密度高，有利于中和颗粒表面电荷形成稳定絮体。王兴军等[79]利用阳离子型聚丙烯酰胺处理煤气化细渣悬浊液时发现，当pH 较大时絮体形状不规则且分散，而随着pH 降低絮体二维分形维数增大，这表明酸性条件下阳离子混凝剂混凝效果更强。

(2)温度。矿浆温度能够显著影响矿物颗粒、水、药剂等多种组分的物化活性及其交互作用，造成颗粒混凝过程及絮体分维性质的差异化。刘云霞[80]发现，当温度在20～80 °C 时，随温度升高煤泥水中絮体的分形维数呈现先增后减或逐渐增加的趋势，并认为温度的适当升高促进了颗粒布朗运动，提高了药剂与颗粒间化学反应速率，进而强化了颗粒间凝聚；而温度过高时，布朗运动加剧增强了絮体的水合作用，导致部分已形成的絮体再次破碎。XIAO 等[81]以硫酸铝为混凝剂处理高岭土悬浊液时发现，当矿浆温度由28 °C 降至2 °C 时，絮体分形维数也降低，并认为温度降低使得水的黏度增加，铝盐难以水解且水解产物与胶体颗粒的黏附作用减弱，导致形成的絮体更加松散。

(3)无机盐离子。某些无机盐离子对絮体分维性质有很大影响。WU 等[82]以用腐殖酸为沉淀剂，通过沉淀浮选法去除废水中Cu2+、Pb2+、Zn2+等重金属离子，发现随着金属离子质量浓度由10 mg/L 增至200 mg/L，絮体的分形维数显著降低。XU 等[83]研究CaCl2对煤和高岭土模拟的煤泥水絮凝行为的影响时发现，随着Ca2+浓度增加，絮体分形维数增加。可见，外界条件不同，混凝过程中形成矿物颗粒絮体的分维特性间也存在显著差异，矿浆物化性质的改变对调控颗粒聚集过程及絮体性质，实现选别指标的优化具有重要意义。

3.3.3水力学条件

混凝过程水力学条件能够显著影响颗粒聚集/分散效果，改变絮体分维特性，并对浮选预调浆及尾矿浓缩沉降等作业环节产生显著影响。搅拌强度和搅拌时间是矿物加工过程中最为常见的水力学条件变量。

(1)搅拌强度。水力扰动能够通过外加物理力场的方式调控体系能量输入，显著影响颗粒间的聚集/分散行为，进而改变颗粒絮体的分维特性。牛福生等[84]研究搅拌流场对赤铁矿絮体的影响时发现，当搅拌转速由700 r/min 增至900 r/min 时，絮体二维分形维数迅速增加；当转速继续增加，絮体分形维数变化较小，这是由于搅拌强度的增加可增大颗粒间碰撞、黏附概率，增加水流剪切力，有利于絮体形成。范桂侠[85]研究油酸钠体系钛铁矿和钛辉石聚集行为时发现，当搅拌转速由0 增至2 100 r/min 时，2 种矿物颗粒絮体的二维分形维数均呈先增后减趋势，但同一搅拌强度下钛铁矿絮体比钛辉石絮体更加密实。

(2)搅拌时间。长时间的搅拌易导致已形成的絮体发生破碎。付嘉[86]利用纳米磁性絮凝剂和助凝剂PAM 处理煤泥水时发现，在最佳搅拌转速条件下，当搅拌时间在2～10 min 时，煤泥絮体分形维数逐渐增加并最终趋于定值。刘利等[87]在最佳搅拌速度下以PAM 为混凝剂处理煤泥水时发现，搅拌时间为10 s时絮体最为密实，而随着搅拌时间进一步延长，絮体分形维数又逐渐降低。

由此可见，矿物加工矿浆混凝工艺环节存在最佳水力学条件，此时矿物颗粒絮体有最密实的结构。开展矿物颗粒絮体分维性质研究，有助于探明不同条件下颗粒聚集/分散行为，揭示絮体性质变化规律，进而实现对矿浆颗粒悬浮、沉降等工艺过程的精准调控。

3.4 分形理论在调浆-浮选及絮体沉降工艺中的应用

3.4.1在调浆-浮选中的应用

适宜的调浆-浮选条件能使目的矿物选择性聚团、脉石矿物充分分散，进而实现目的矿物高效浮选回收。调浆-浮选过程中矿物颗粒间会发生复杂的聚团-破裂-重组现象，基于调浆-浮选过程研究能够有效揭示调浆-浮选过程中不同颗粒间聚集/分散状态的变化规律，深化对调浆-浮选强化矿物浮选作业的内在认识，甚至达到指导和调控浮选过程的目的。分形理论及其方法能够有效用于调浆-浮选过程中矿物颗粒聚集/分散行为与絮体性质的研究，是揭示调浆-浮选过程中颗粒聚集/分散状态的有效手段。

微细颗粒选择性疏水聚团是实现不同种类物料浮选分离的前提。实践中，通常基于分形理论探索不同操作变量下微细矿物颗粒聚集形态变化规律，进而指导后续浮选作业。金属矿浮选领域，范桂侠[85]研究钛铁矿与钛辉石选择性聚团浮选时发现，相同油酸钠用量条件下，钛铁矿絮体分形维数比钛辉石絮体大，表明油酸钠更有助于促进钛铁矿的选择性聚团，从而实现钛铁矿的浮选分离；ZHANG 等[88]通过溶气法浮选纳米二氧化钛颗粒时发现，当二氧化钛絮体的分形维数最大时，对应浮选回收率最高。洁净煤浮选研究领域，赵静等[89]发现非极性油能够使超细煤颗粒发生选择性聚团，通过调节机械搅拌强度可改变煤颗粒絮体密实程度，当煤絮体二维分形维数最大时,浮选精煤产率最高且超净煤产品灰分最低；梁龙[90]在研究煤的选择性絮凝浮选时同样发现，煤絮体分形维数的增加有助于提高浮选精煤产率的同时降低产品灰分。由此可见，调浆-浮选过程中，矿物絮体的分形维数性质与最终的浮选指标密切关联，调浆-浮选过程中矿物絮体分形维数的深入研究有助于选别工艺流程的升级改造、促进综合选别指标的提升。

3.4.2分形理论在絮体沉降中的应用

絮体沉降行为与其分维性质也密切关联，基于分形理论探究不同絮体(群)沉降特性有助于深化对沉降过程的理解，相关研究成果为能够调控矿物颗粒宏观沉降行为提供借鉴。孙浩等[91]研究铅锌矿尾矿絮凝沉降行为时发现，分形维数大的絮体有较高的沉降速率；黄彦龙[92]以石英为载体，絮凝微细粒高岭石尾矿时也发现了同样的规律；李冬梅等[93]在研究架桥絮凝作用下泥沙絮体的形成过程时发现，絮体分形维数较大，密实度越高，沉降脱水性能越好。

此外，在过滤操作前高浓度矿浆悬浊液中矿物颗粒絮体的沉降阶段，絮体结构能够显著影响过滤滤饼性质，进而影响最终过滤效果，例如ALAM 等[74]发现在混凝剂最佳用量下，煤矸石絮体分形维数大且强度较高，这有助于形成渗透率高、含水量适中的滤饼，进而提升过滤效率。故一般认为，当絮体分形维数较大时，其沉降性能更优越，反之则不利于沉降及过滤。需要指出的是，对矿物絮体分形维数的深入研究有助于选别工艺流程的升级改造、促进综合选别指标的提升，但该方向的研究总体仍停留在实验室阶段，尚未实现规模性工业应用。

4 结语与展望

分形维数是分形的度量指标，用于描述分形体不规则程度及其在空间中的填充程度，在实践中应结合分形体特征选取适宜的测量计算方法。

目前，分形理论已广泛应用于矿石拣选、矿石碎磨、调浆-浮选、沉降及过滤等工艺环节的过程研究。矿石拣选领域，主要聚焦于矿石中有用矿物含量的分形分布规律研究；矿石碎磨领域，主要涉及碎磨过程矿石形态分形特征研究；调浆-浮选与沉降领域，主要体现在对矿浆混凝行为及不同条件变量下絮体分维特性研究；过滤领域，相关研究包括过滤参数、絮体分形结构和滤饼孔隙分形结构间的关系及滤饼结构探究等。分形理论研究深化了对矿物加工工艺过程的认识，实现了对不同工艺环节的过程调控与优化，并最终提升了综合作业指标。

分形理论在矿物加工领域的应用为剖析各类具有自相似性等分形特征的工艺环节过程机理提供了新的研究方法。但不可否认，现有研究仍存在不足，且大部分相关研究成果尚未投入实际生产，因此分形理论在矿物加工领域仍有较大的发展空间。理论研究方面，由于基于分形理论的混凝行为研究发源于水处理领域，且矿浆悬浊液与废水悬浊液性质间存在部分差异(如初始颗粒种类及粒度、絮体粒度、液体环境等)，尤其是混凝动力学及絮体分形结构生长模型研究方向鲜有选矿工作者涉足，因此可对该领域进行更深入的探索。工业实践方面，分形理论的应用前景主要体现在矿山与选矿过程智能化方向：在矿石拣选领域，基于有用矿物在自然矿石中分形分布规律可预测拣选经济效益指标，该成果可应用于选厂实际生产中，以提高生产效率，节约人力物力。在矿石碎磨领域，除人工优化设备参数外，还可考虑在破碎机出料口及磨机内部添加传感器，对矿石粒度分布及颗粒形状进行在线监测，通过算法分析颗粒粒度分布分形维数及形状分形维数的变化规律控制碎磨过程，以将矿石精准碎磨至目标粒度，节约碎磨能耗。在过滤领域，可考虑在固液分离设备上添加图像识别系统采集滤饼孔隙分维信息，以实现对过滤压力及滤饼局部加药的智能控制。此外，基于絮体分形维数的智能投药系统已应用于水处理领域，即利用摄像装置完成絮体图像采集，再通过自编程序计算絮体分形维数，判断絮体结构特征，完成自动加药，实现了对水处理混凝过程的在线监控以及对絮体分形结构的灵活控制[94]，该研究同样可应用于矿物加工调浆-浮选、沉降过程，除控制加药量和加药时间外，还可考虑实现对矿浆环境和搅拌条件的智能调控。

综上，分形理论与传统选矿理论、研究方法的高效融合是当前的发展趋势，相关研究成果也必将有益于矿物加工技术的升级与智能化发展，为资源节约、环境友好、可持续发展的矿物加工工程体系的构建奠定基础。