低测试逃逸的晶圆级适应性测试方法

梁华国 曲金星 潘宇琦 汤宇新 易茂祥 鲁迎春

(合肥工业大学微电子学院 合肥 230009)

1 引言

随着集成电路技术的发展，晶体管的尺寸不断地减小，其制造成本也在减少。但是每个晶体管的测试成本并没有随着工艺的进步而降低。随着电路板变得越来越复杂，测试成本占总制造成本的很大一部分，有时甚至占主导地位[1]。同时芯片集成度越高，后期的测试过程越复杂，测试成本也就越高，因此在芯片制造的前期，比如：晶圆允收测试(Wafer Acceptance Test, WAT)、晶圆探针测试(Circuit Probe, CP)等阶段找到存在故障晶粒可以节省整个测试流程的测试成本。在晶圆中相邻位置的晶粒制造工艺相似，所以已知的合格晶粒(Known Good Die, KGD)信息可以作为识别故障晶粒的重要判断依据。在晶圆适应性测试过程中，为了降低测试成本需要对晶粒的测试项数量或者顺序进行调整，删减测试项数量可能会导致故障晶粒产生测试逃逸。晶圆适应性测试是指通过对历史测试数据的分析，对后续的测试条件、测试内容等进行优化，在保证测试质量的同时，又可以降低测试成本[2]。在晶圆测试过程中，测试项指的是要测试的电气指标，如电阻、电容、电流等，而参数则是这些测试项的具体数值，如静态漏电流、反向击穿电压和输出电压等参数。在晶圆制造过程中，即使制造工艺完全相同，由于生产设备和环境等不可控因素会导致同一批次之间不同的晶圆或者同一块晶圆中相邻位置的晶粒出现参数差异的情况[3]。因此如何从邻域参数差异方面权衡测试成本和测试逃逸成为集成电路测试领域的重大挑战。

为了应对这一挑战，一部分学者对晶粒测试项相关性进行研究。该研究主要是分析测试项之间存在的线性或非线性关系，通过统计或机器学习的方法对原测试内容进行优化。卡内基梅隆大学相关学者使用贪心算法从原有测试项中进行循环迭代，找到高故障覆盖率的测试集[4]。但是这种方法可能会导致过拟合现象、模型泛化能力下降、产生过多的测试逃逸和产量损失。杜克大学相关学者提出使用贝叶斯网络模型，基于测试项之间的互信息和马尔科夫毯的原理选择测试子集，以此来降低测试成本[5,6]。东华大学相关学者通过分析使用最大相关性最小冗余项算法分析测试项和测试结果之间的关系，并通过深度信念网络模型准确率选择最终的测试集[7]。该类研究往往为了降低测试成本，会对测试内容进行删减，从而导致晶粒出现测试逃逸。

另一部分学者对相邻位置晶粒进行研究。这类研究主要是分析待测晶粒与邻域晶粒存在的差异性以此找到存在测试逃逸的晶粒。加州大学相关学者提出使用晶粒测量值和邻域晶粒的参数均值得出的残差向量作为待测晶粒的特征、邻域晶粒的参数值中位数作为新的特征，使用双边滤波的非线性滤波方法检测存在可能测试逃逸的晶粒[8–10]。奈良科学技术大学相关学者对晶圆中不同位置晶粒之间的变化进行研究，提出使用高斯线性模型分析相邻晶粒之间差异性，分析可能存在测试逃逸的晶粒[11]。新加坡国际大学相关学者分析批次间以及批次内晶圆由工艺波动导致的参数差异，提出使用高斯混合模型对晶粒进行分类[3]。西安电子科技大学相关学者提出相邻晶粒的参数偏差和邻域参数波动结合的方法找到可能存在测试逃逸的晶粒[12]。相邻位置晶粒的研究更多是根据相邻晶粒的测试结果或者参数值分析晶粒是否存在测试逃逸。

综上所述，为了降低晶圆的测试成本，本文提出有效测试集筛选的测试方法。为了提高测试质量，本文提出邻域参数波动程度的指标，对有邻域参数波动的晶粒采用邻域参数差异放大化的处理方法，将合格晶粒和故障晶粒之间存在的微小差异放大化，从而提高机器学习模型的分类准确率，减少测试逃逸晶粒的数量。无邻域参数波动的晶粒采用机器学习对有效测试集建模的方法，降低测试逃逸和产量损失的风险。本文方法的平均测试项减少率为40.13%，测试逃逸率为0.009 1%。

2 研究基础

2.1 参数波动

在晶圆生产制造过程中，无法避免工艺波动的产生，从而导致了晶圆中参数之间出现不同程度的波动情况[3]。通常相关学者会对晶圆整体参数波动进行分析，找到晶圆中存在晶粒参数波动异常的大致位置，以此找到存在测试逃逸的晶粒，并对晶圆制造过程进行优化和改进。无论是同一块晶圆或者同一个批次，相同参数的测量值也有变化。如图1所示为工艺波动导致3个批次的某一参数均值对比和批次内3块晶圆参数均值对比。从图中可以看出，3个批次间的参数均值是不同的，在批次内部不同晶圆的参数均值也是不一样的。邻域参数表示待测晶粒相邻位置晶粒的参数。全局参数波动的分析往往会掩盖邻域参数波动的存在，无法利用其邻域参数之间的微小差异对晶粒进行分析，从而导致了待测晶粒可能会出现测试逃逸的风险。

邻域参数波动是基于晶圆中相邻位置晶粒的空间相关性在参数方面的表现形式。如图2所示，邻域参数波动表示在相邻位置范围内晶粒的参数呈现出波动的程度。通过分析参数波动可以掌握晶粒质量变化规律，并依据晶粒不同邻域参数波动程度使用不同的预测模型，可以减少晶粒产生测试逃逸的风险。

图2 邻域参数波动图

2.2 参数差异放大化

参数差异性放大化是将晶粒原有参数值转换为差异大的特征值来表示。原有参数值之间的差异性很小，有时无法准确地识别出合格晶粒和故障晶粒之间的不同，容易在测试过程中产生测试逃逸和产量损失。对于存在邻域参数波动的晶粒，存在不同的波动情况和邻域参数之间的差异性。如果使用统计学的方法对邻域参数波动进行异常波动筛选，会导致晶粒出现严重的测试逃逸和产量损失。比如：合格晶粒邻域参数波动很大会被误判故障晶粒；故障晶粒邻域参数波动很小，会被误判为合格晶粒。因此需要结合邻域参数之间存在的微小差异对晶粒进行建模，而机器学习对于这种数据之间存在微小的差异无法进行准确的建模，所以对邻域参数进行差异放大化处理，则可以有效解决这种问题。

待测晶粒参数与邻域参数之间的差异性可以通过残差向量进行表示，通过计算待测晶粒的测量值和邻域晶粒参数的均值之间的差值，并将其作为晶粒的特征进行建模，可以有效找到存在测试逃逸的晶粒[8]。但是这种计算方法准确度容易被邻域晶粒参数中存在的异常值所影响，而中位数既可以表示邻域晶粒参数的分布特征，又可以避免邻域参数中异常值对于量化过程的影响。

2.3 质量预测模型

质量预测模型主要是使用历史晶圆的晶粒参数信息或者坐标信息和测试结果使用机器学习训练出的预测模型[13,14]。本文方法中既使用了历史晶粒的测试项信息训练的特征参数质量预测模型，又使用了其空间坐标信息训练空间波动质量预测模型。如图3所示为使用历史晶粒进行随机森林建模的过程。本文采用随机森林算法对晶粒集进行自举采样并对每个样本集选取不同的有效测试项进行建模，从而避免模型过拟合，且每个子模型之间并行进行，模型泛化能力强。特征参数质量预测模型是针对没有邻域参数波动的晶粒训练的模型。将历史测试数据中的有效测试集作为特征，测试结果作为标签，使用随机森林训练模型。空间波动质量预测模型是针对有邻域参数波动的晶粒训练的模型。将经过邻域参数差异放大化的有效测试集作为新特征，测试结果作为标签，使用随机森林训练模型。

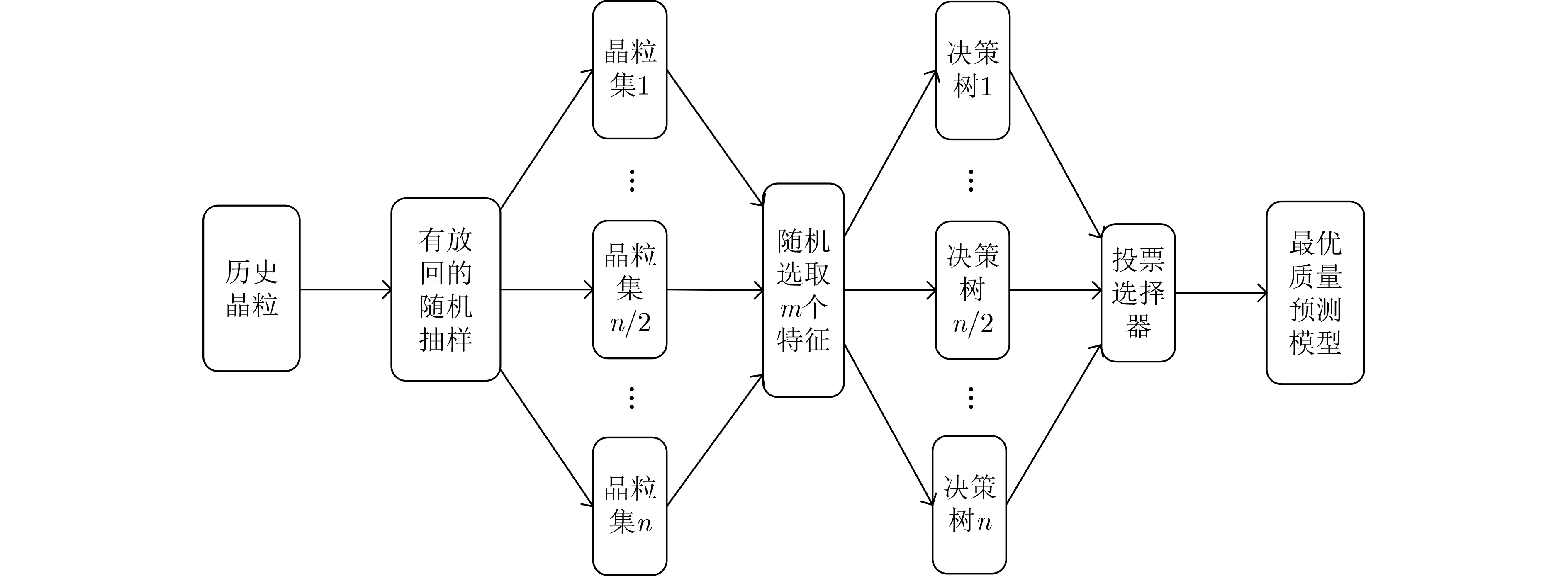
图3 随机森林建模过程

3 低测试逃逸的晶圆级适应性测试方法

本节将详细描述所提出的低测试逃逸率的晶圆级适应性方法建模流程。如图4所示，该方法主要分为3个部分：(1)测试集选择；(2)邻域参数波动性分析；(3)邻域参数差异放大化。通过分析历史测试数据集所包含的测试项信息和位置信息，对晶粒进行分类建模。

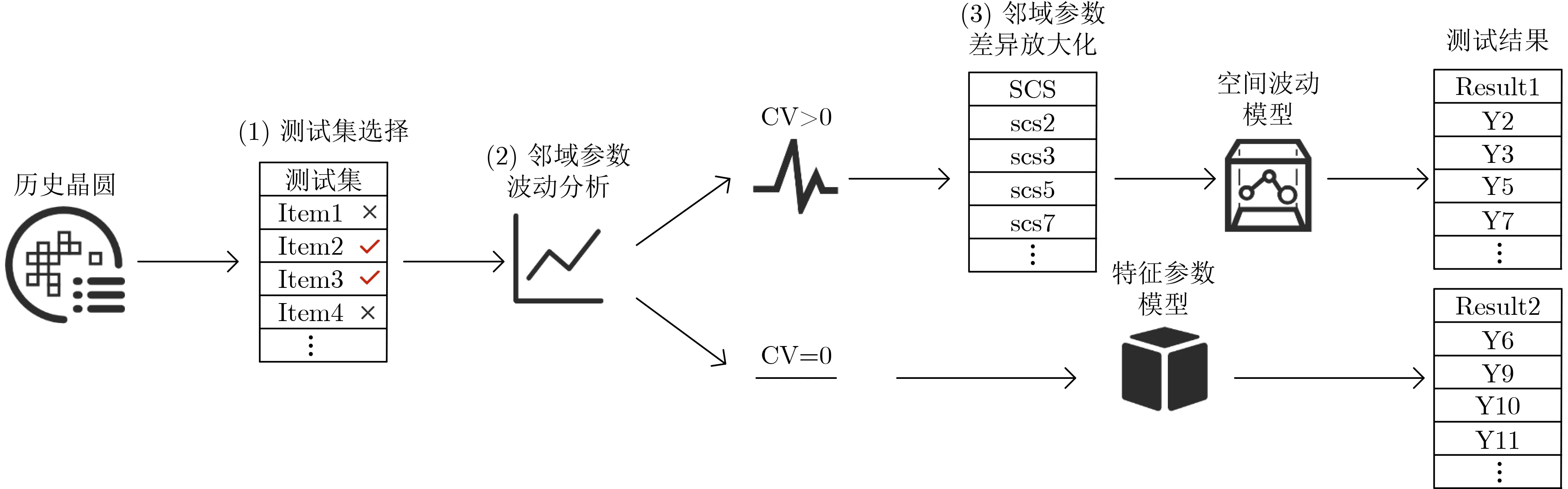
图4 基于低测试逃逸的晶圆级适应性测试方法建模流程

在第(1)部分中，根据批次级晶圆历史测试数据进行有效测试集筛选，选择可以检测故障晶粒的测试集。这些有效测试集在邻域空间内存在有无参数波动两种情况。因此需要在(2)中对邻域参数波动进行分析，并将待测晶粒进行分类。对于存在邻域参数波动的晶粒，其参数之间存在大量的信息，需要在(3)中对其进行邻域参数差异放大化处理，然后使用新特征建模进行质量预测；而对于无邻域参数波动的晶粒，通过特征参数模型对其进行质量预测。

3.1 测试集选择

(1)数据预处理

由于晶圆历史测试数据存在大量缺失值，对于邻域参数波动分析时和训练模型时会产生不良影响，需要对于历史测试数据的缺失值进行处理。在ATE测试晶圆过程中，遵循“首败即停”的原则，即在某一个测试项检测到故障晶粒时，后续的测试内容就不需要进行，所以导致测试数据表中会出现大量的缺失值。对于这些缺失值，采用同一测试项下无故障晶粒的参数值的中位数进行填充，从而可以让历史数据集完整以便进行下一步的邻域参数波动分析和邻域参数差异放大化处理。

(2)有效测试集筛选

有效测试集筛选的目的是获得一个可以降低测试成本同时减少测试逃逸风险的测试集。有效测试集将用于下一步的邻域参数波动性分析和邻域参数差异放大化处理。本文有效测试集选择主要是通过对历史晶圆测试数据进行分析，选择出可以检测到历史晶圆中所有故障晶粒的有效测试集。然后使用该测试集对待测晶圆进行测试。

如图5所示，对于批次历史晶圆测试数据，需要检测每块历史晶圆其测试项ti测试到故障晶粒的数量λ是否为零，若是λ̸=0 ， 则证明该测试项ti为有效测试集的子集，反之则说明该测试项ti不能检测到故障晶粒。当测试项ti循环迭代至所有历史晶圆时，可以得到最终的有效测试集。本文中的测试项对应为参数测试中某一具体测试内容(如：漏电流，反向击穿电压等等)，且每个测试项并不针对某一具体故障类型。

图5 有效测试集筛选流程

3.2 邻域参数波动性分析

本文提出了以变异系数(Coefficient of Variation, CV)来表示晶圆中存在的邻域参数波动的情况，变异系数越小，表示其邻域参数波动越小，参数趋于稳定；反之，变异系数越大，表明其邻域参数波动越大，待测晶粒的参数越有可能异常。如图6所示，本文中邻域参数的计算都是以3×3的窗口进行的，关于晶粒空间相关性研究的邻域窗口的选择是基于文献[15]中关于晶圆空间特征与质量之间的关系。CV是邻域晶粒参数的标准差 SDij和均值µij的比值，它既消除了不同参数之间量纲的差异，又代表待测晶粒邻域参数的波动程度。其中邻域参数均值µij为

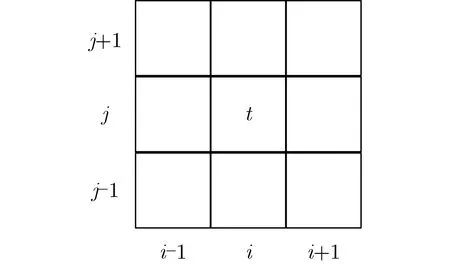
图6 晶粒t 的邻域晶粒分布

其中，Pab表示的是邻域晶粒的参数值，i-1≤a ≤i+1,j-1≤b ≤j+1,n表示邻域晶粒的个数。i表示晶粒在晶圆中X轴的坐标，j表示晶粒在晶圆中Y轴的坐标。邻域参数标准差S Dij为

最后CV的计算方法为

其中，C Vij表示的是待测晶粒t的邻域参数波动大小，需要注意的是，在计算过程中邻域晶粒的参数值可能会出现异常值的情况，为了保证邻域参数波动量化的稳定性，需要在计算过程中去掉最大值最小值。邻域参数波动性分析中变异系数和标准差对比的优势在于，当多个邻域晶粒参数的标准差一样而平均值不一样时，标准差无法准确地反映出不同晶粒测试参数的波动程度，而变异系数可以准确反映其波动程度。而且在比较两组量纲不同或均值不同的数据时更精确，且不需要参考测试数据的均值。

通过对于晶粒邻域参数波动的分析，可以将晶粒分为有无邻域参数波动的晶粒：有邻域参数波动晶粒，这类晶粒和邻域晶粒之间存在参数差异性，需要通过残差向量和邻域参数差异放大化将其特征进行放大分析；无邻域参数波动晶粒，其制造工艺相同，可以通过特征参数模型对其进行质量预测。

3.3 空间相关性强度

本文提出了以空间相关性强度(SCS)表示待测晶粒的邻域空间相关性的强度，如果待测晶粒参数和邻域晶粒参数之间差异性越大，晶粒的邻域空间相关性越弱，该晶粒是测试逃逸可能性就越大。在晶圆的生产制造过程中，缺陷会导致重要电压、电流等参数“阶跃”，而不是像正常晶粒参数那样逐渐变化。这种突然的变化会表现为负尖峰(晶粒参数低于邻域)或正尖峰(晶粒参数高于邻域)等异常现象[16]。空间相关性强度可以将晶粒中存在这种异常现象进行量化，并将存在测试逃逸的晶粒其特征放大化以便机器学习可以更加准确地获取存在测试逃逸晶粒的特征。其中“其特征”指的是测试逃逸的晶粒和合格晶粒参数间存在的测试项响应上的微小差异。

残差向量R Vij的计算方法由式(4)表示

其中，Pij表示为待测晶粒的参数值，Mij表示为邻域晶粒参数的中位数。这里采用以中位数表示领域参数的数据分布特点，而不是采用均值。因为实际生产过程中工艺波动对晶粒产生的影响，每个晶粒周围无法避免异常值的出现。若采用均值的方法，异常值会造成邻域参数计算偏差过大，而中位数既可以减少异常值对于邻域参数数据分布的影响，又可以表示邻域参数的数据分布特点。

空间相关性强度(SCS)的计算方法由式(5)表示

其中，R Vij表示为待测晶粒参数值与邻域晶粒参数中位数的差值，C Vij表示的是待测晶粒邻域晶粒参数波动的大小。

通过邻域参数波动分析，以CV的值为分类标准可以将历史晶圆中和待测晶圆中的晶粒分为有无邻域参数波动的晶粒。有邻域参数波动晶粒通过邻域参数差异放大化的过程将其参数之间的差异放大化后，以空间相关性强度S CSij替代原有的晶粒参数值Pij，将历史晶圆的测试结果作为标签，空间相关性强度S CSij作为每个晶粒的特征，使用随机森林建立空间波动模型。

对于无邻域参数波动晶粒，以历史晶圆中无邻域参数波动(CV=0)晶粒的参数值Pij作为该类晶粒的特征，以测试结果为标签，使用随机森林建立特征参数模型。通过该模型可以有效解决空间波动模型分析对于这类晶粒测试逃逸和产量损失过高的问题。

在测试过程中，待测晶圆通过邻域参数波动分析，将里面的晶粒分为有无邻域参数波动的晶粒，有邻域参数波动晶粒使用空间波动模型对其进行测试得到测试结果Result1；无邻域参数波动晶粒使用特征参数模型进行测试得到测试结果Result2。

4 实验结果

4.1 实验平台设置以及数据描述

本次实验运行环境为Intel i7-7 700 CPU, 16 GB运行内存，Windows 10系统。实验所用仿真平台为python3.8，主要用到的库为Numpy库、Pandas库和Scikit-learn库。实验数据选取了来自实际工业生产过程中3个不同批次的模拟芯片测试结果，每个批次12块晶圆，总计1 485 228块晶粒。本次实验中随机抽样的每个批次的5块晶圆数据进行建模，剩余的7块晶圆数据用于验证模型。实验数据具体信息如表1所示。

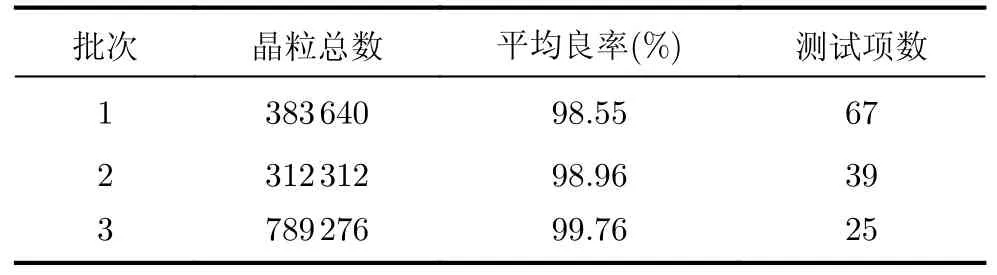
表1 实验数据分布

4.2 邻域参数波动性分析结果

本文以变异系数(CV)来衡量晶粒的邻域参数波动大小。如图7所示为批次1中某块晶圆部分晶粒的邻域参数波动图。从图中可以看出，相邻位置晶粒参数之间的差异性很小，使用邻域参数波动更能反映出晶粒之间不同。有邻域参数波动晶粒邻域参数波动大小不同，再结合测量值和邻域晶粒参数中位数的差值，可以将其作为晶粒的新的特征，这类特征将更好地区分合格晶粒和故障晶粒之间的不同。无邻域参数波动晶粒的特点是邻域晶粒参数稳定，但是因为不是全集测试，无法保证未测试的参数是否影响其最终的预测结果。如果使用邻域晶粒故障率(Bad Neighbor Ratio, BNR)等空间相关性[17]去判定，会导致合格晶粒被判定为故障晶粒，故障晶粒被判定为合格晶粒。通过历史数据中没有邻域参数波动晶粒的参数和测试结果建模，可以减少测试逃逸和产量损失。

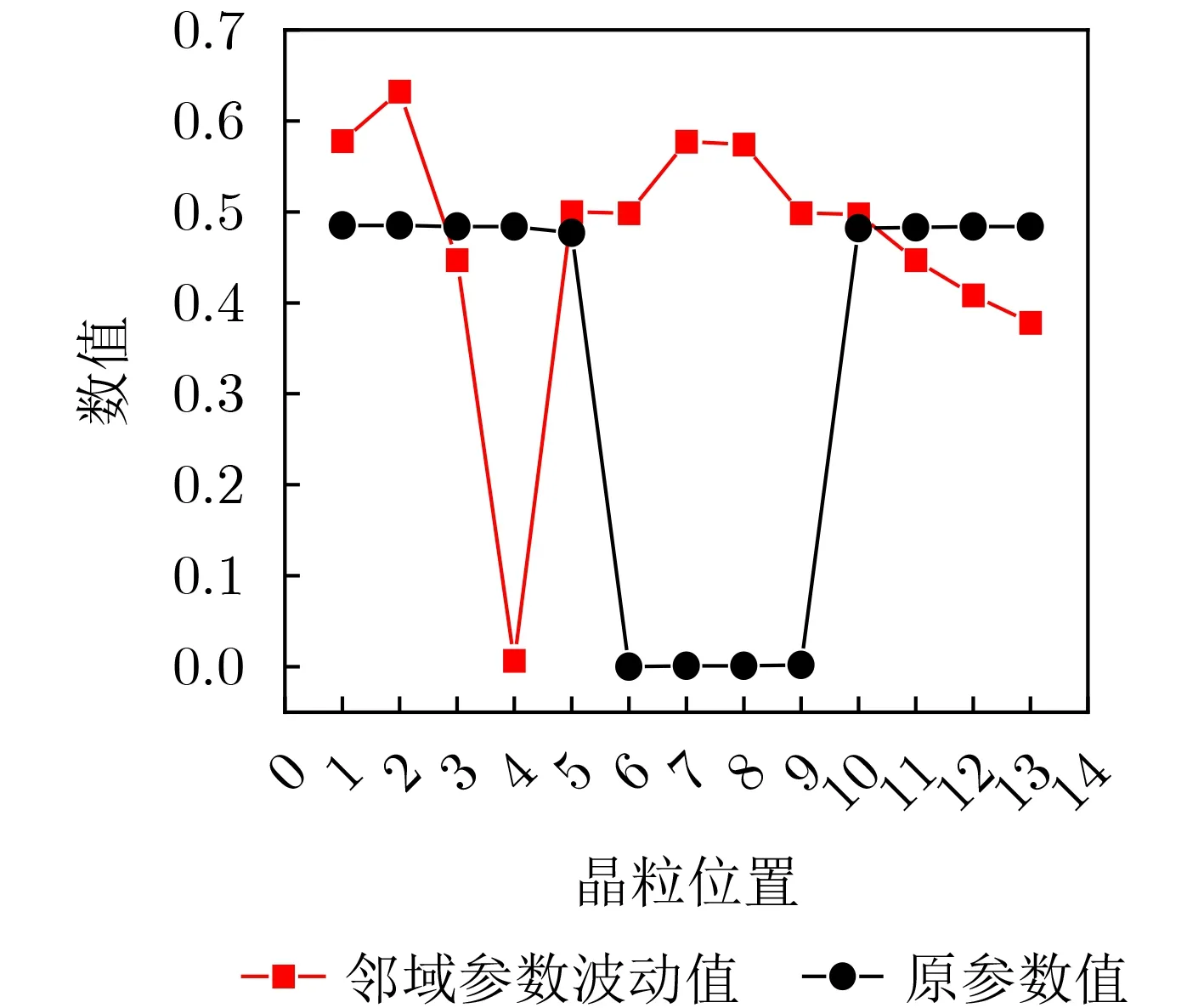
图7 晶粒邻域参数波动

4.3 邻域参数差异放大化结果

对于有效测试集，相同测试项之间的参数差异性不同，其里面隐藏着很多有效的信息。对于每个批次中有邻域参数波动晶粒使用邻域参数差异放大化前后实验结果对比，如图8所示，在邻域参数差异放大化前晶粒参数值之间的差异性很小，无法区分合格晶粒和故障晶粒的不同，而在邻域参数差异放大化后，晶粒参数值之间的差异性明显变大，合格晶粒和故障晶粒之间的特征变得更加明显，更容易找到存在测试逃逸的晶粒。

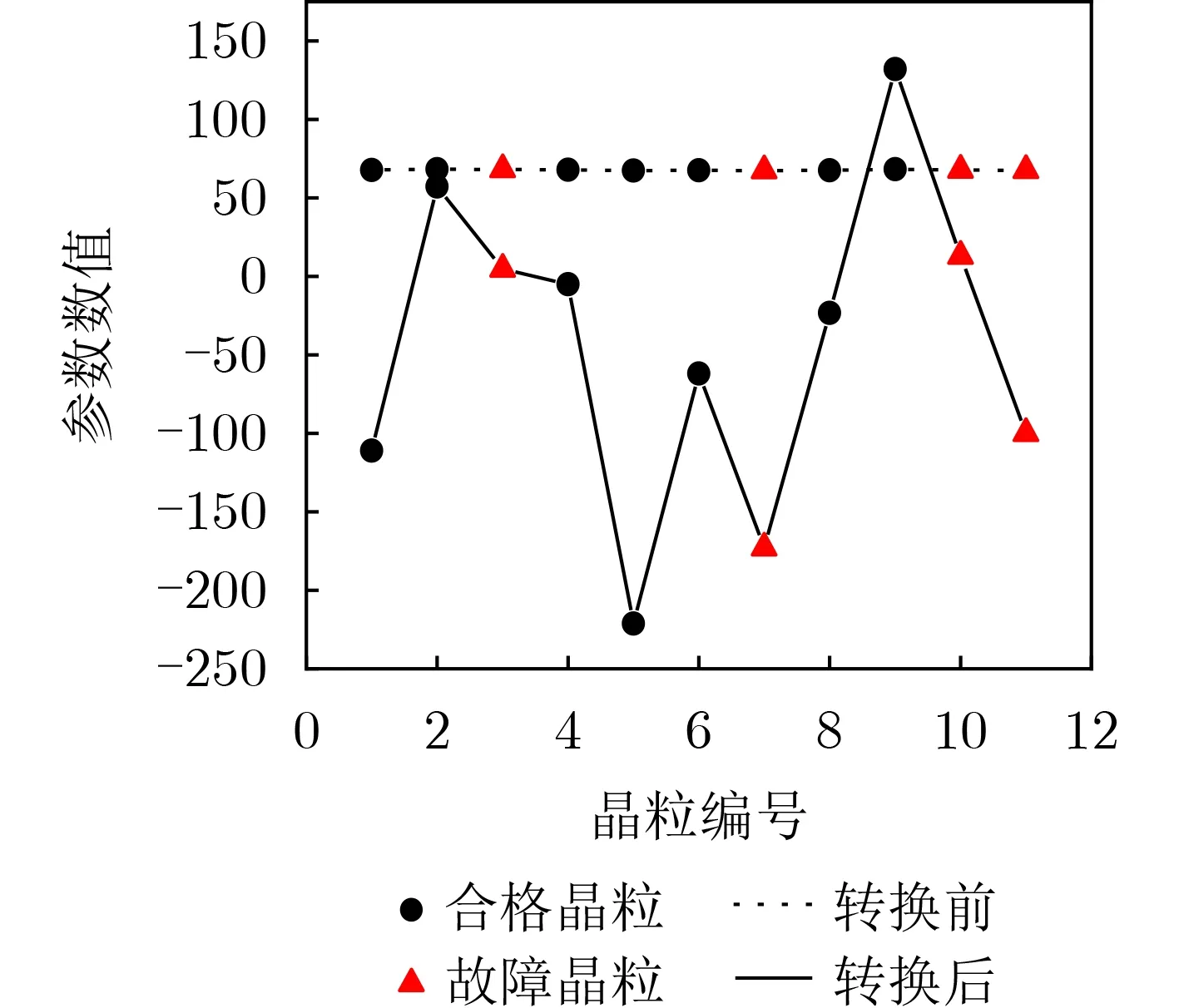
图8 参数差异放大前后数值对比

如图9所示为批次1中7块晶圆邻域参数差异放大化前后建模的测试逃逸晶粒数量对比和测试逃逸减少率。从图中可以看出，在每块晶圆上进行邻域参数差异放大化后，存在测试逃逸的晶粒数量都明显少于邻域参数差异放大化前建模的数量。经过邻域参数差异放大化处理之后，存在测试逃逸的晶粒参数特征被明显放大了，这样更能捕捉到合格晶粒和故障晶粒之间的不同差异。

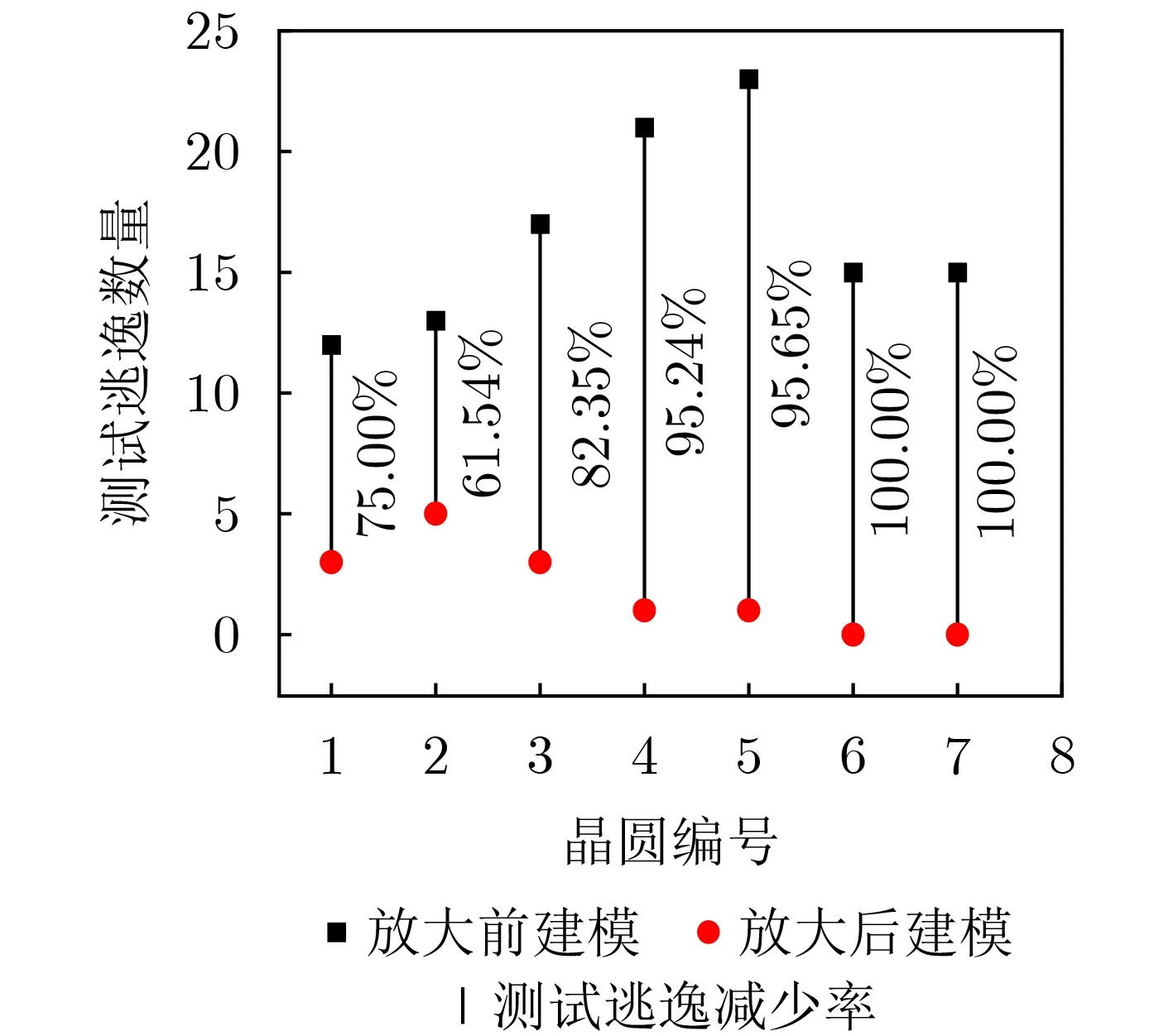
图9 参数差异放大前后建模测试逃逸数量对比

如图10所示为邻域参数差异放大化前后建模的产量损失数量对比和产量损失减少率。从图中可以看出，在每块晶圆上进行邻域参数差异放大化后，存在产量损失的晶粒数量都明显少于邻域参数差异放大化前建模的数量。因此本文方案在减少晶粒测试逃逸的数量，同时并没有增加其产量损失的数量。

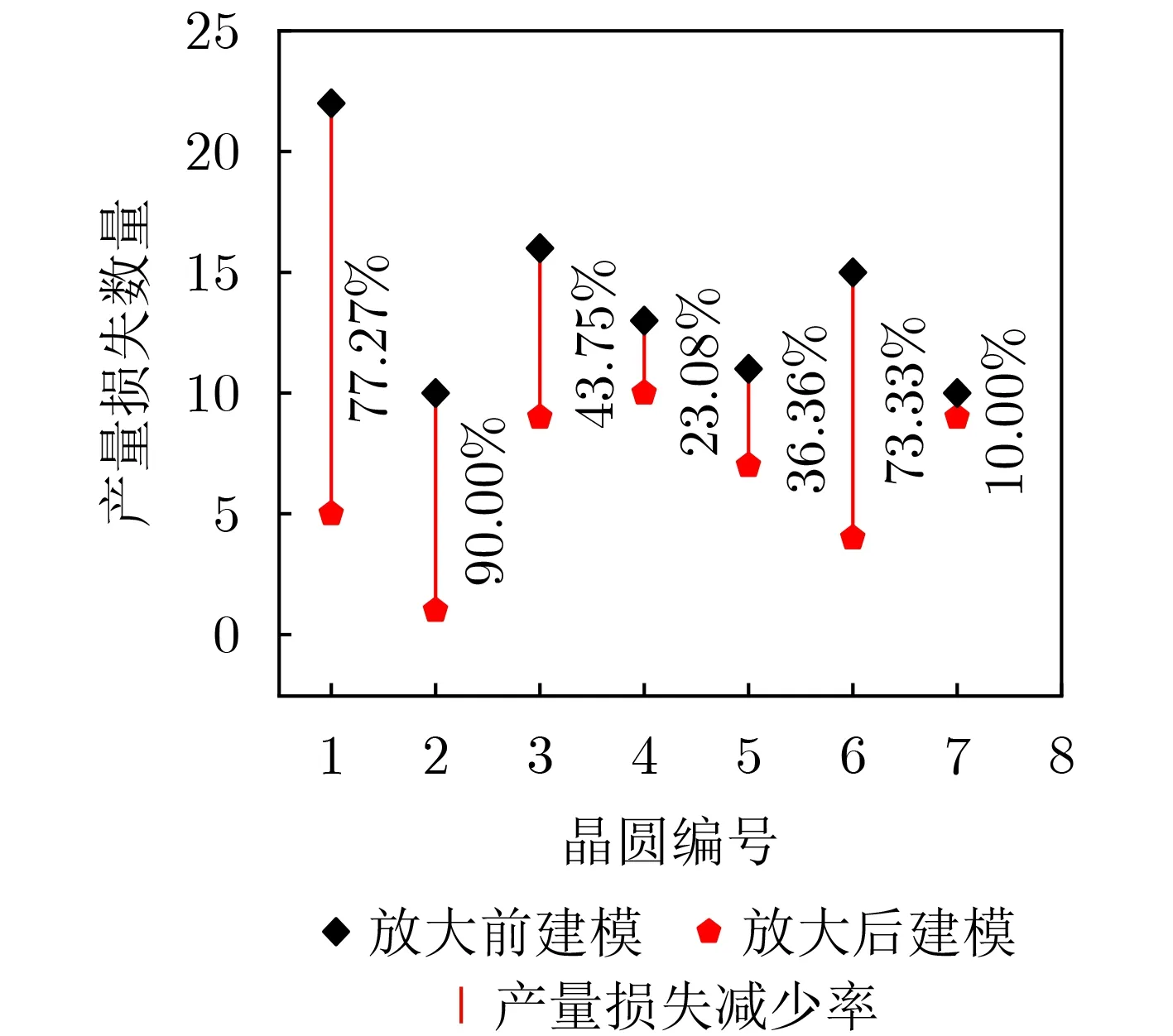
图10 参数差异放大前后建模产量损失数量对比

4.4 方案对比

本次实验与2020年提出的过滤式和封装式相结合的测试方法[7](方法1)和2022年提出的位置相关性筛选方法[12](方法2)进行比较，实验主要比较了测试项减少率(TIRR)、测试逃逸率(TER)、产量损失率(YLR)3个指标。测试项减少率表示与标准测试(标准测试指的是使用原测试计划中所有的测试项)相比节省测试项的比例。该指标的计算公式为

其中，N表示的是晶圆中待测晶粒的数量，TS表示有效测试集的测试项数量，TA表示测试全集中测试项的数量。TIRR的大小只与有效测试集筛选中测试项的数量有关，而与晶圆中晶粒数量无关。

测试逃逸率表示故障晶粒被预测为合格晶粒的数量占待测晶圆中总晶粒数量的比例，其计算公式为

其中，NE表 示测试逃逸晶粒的数量，N表示待测晶圆中晶粒的数量。测试逃逸率越低表示测试完成的晶圆中故障晶粒数量越少，但并不能保证测试质量越高，测试质量与产量损失率也有关。

产量损失率表示合格晶粒被预测为故障晶粒的数量占待测晶圆中晶粒数量的比例，其计算公式为

其中，NL表示产量损失晶粒的数量，N表示待测晶圆中晶粒的数量。

从表2可以看出，本文方法和方法1相比TIRR虽然增加了11.28%，但是测试逃逸率比方法1降低了84.04%，产量损失率降低了59.35%。本文方法和方法2相比TIRR降低了11.94%，测试逃逸率比方法2降低了51.39%，产量损失率降低了50.13%。因此本文提出方法在降低晶圆测试成本同时保持较低的测试逃逸率。在实际的晶圆制造过程，无法避免工艺波动的产生，从而也无法避免参数波动的发生，因此保证了本文所提方法的适用性。

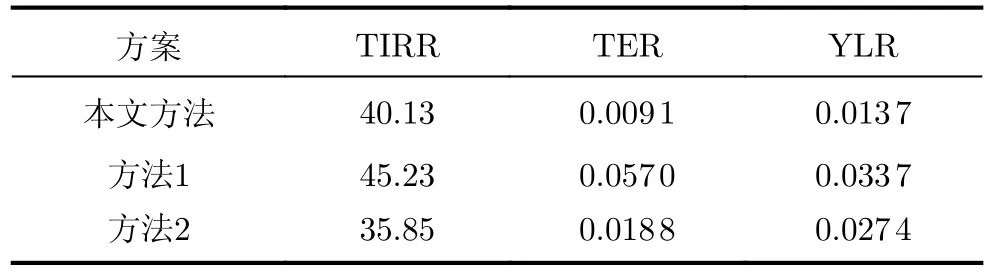
表2 对比实验结果(%)

5 结束语

针对集成电路越来越复杂，测试成本日益增多，测试质量要求越来越高的问题。本文提出了一种低测试逃逸的晶圆级适应性测试方法用于降低晶圆测试成本，减少晶粒测试逃逸的数量。通过有效测试集选择可以降低待测晶圆测试成本。同时对其进行邻域参数波动分析区分有无邻域参数波动晶粒，对有邻域参数波动晶粒进行邻域参数放大化处理，放大合格晶粒和故障晶粒之间参数差异性，提高模型的准确率，减少测试逃逸和产量损失。对无邻域参数波动晶粒采用有效测试集建模方法保证其测试质量。本文方法的平均测试项减少率为40.13%，测试逃逸率为0.009 1%。