OpenPARF: 基于深度学习工具包的大规模异构FPGA开源布局布线框架

麦 景 王嘉睿 邸志雄 林亦波(北京大学计算机学院 北京 100871)

②(北京大学集成电路学院 北京 100871)

③(西南交通大学信息科学与技术学院 成都 611756)

1 引言

FPGA因其可编程性、高并行性以及低功耗得到了广泛应用[1]。然而，随着现代FPGA规模的逐渐增大，FPGA设计工程师必须依靠FPGA计算机辅助设计(Computer Aided Design, CAD)工具来完成FPGA的设计。FPGA CAD的主要流程包括设计描述、逻辑综合、工艺映射、物理实现和比特流生成[2]。其中，物理实现主要包括布局和布线等步骤，决定逻辑单元在FPGA上的位置以及连线之间的延迟。物理实现中的布线部分是FPGA CAD流程中用时最长的部分，占到整个流程的41%～86%[3]。因此，物理实现是决定最终电路性能的关键步骤，其质量和效率直接影响FPGA CAD工具的竞争力。

工业界主流的FPGA厂商，如Xilinx和Intel，采用自研的Vivado和Quartus FPGA CAD工具。这些工具均与FPGA厂商的硬件架构强绑定，难以迁移到其他FPGA架构。相较之下，开源FPGA CAD工具因其算法透明，方便2次开发，成为FPGA设计工程师的另一个选择。当前学术界知名的开源FPGA CAD工具 VTR(Verilog-To-Routing)[4]能够从Verilog网表生成FPGA布局布线的结果。然而，VTR使用的布局布线算法较为陈旧，仍然在采用基于模拟退火的算法，导致性能和效率无法满足大规模FPGA设计的需求。此外，VTR简化了布线架构，没有考虑FPGA逻辑单元输入输出引脚的逻辑不等价性，无法适用于越来越复杂的FPGA架构。

本文提出一个开源的FPGA布局布线框架Open-PARF (Open-source Placement And Routing Framework)。OpenPARF支持在工业级FPGA架构下读入电路网表，生成布局布线结果。该框架基于深度学习工具包PyTorch实现，通过底层C++/CUDA算子结合上层Python接口的方式，支持CPU平台运行和GPU加速，兼具Python的灵活性与C++/CUDA的高效性。在布局算法方面，本文采用了一种新型非对称多静电场系统和多层拉格朗日松弛方法，以处理FPGA布局问题中的复杂约束。在布线算法方面，本文面向现代FPGA的复杂布线架构，采用两阶段布线算法，支持FPGA逻辑单元各引脚逻辑不等价等灵活场景，可实现逻辑单元级别的布线。本文的主要贡献总结如下：

(1) 提出开源的FPGA布局布线框架Open-PARF。本框架支持在工业级FPGA架构下读入FPGA网表，并生成布局布线后的FPGA结果。

(2) 提出一种基于新型非对称多静电场系统的FPGA布局算法，并通过多层拉格朗日松弛方法处理FPGA布局问题中的复杂约束。

(3) 提出一种逻辑单元级别的FPGA布线算法，通过对FPGA布线资源的详细建模和全局/详细两阶段布线，支持逻辑单元引脚逻辑不等价等灵活场景，有效减少布线拥塞。

(4) 与学术界最先进的布局布线工具相比，Open-PARF可减少0.4%～12.7%的布线线长，并实现两倍以上的布局效率提升。

本文的组织结构如下：第2节介绍FPGA的布局布线架构和挑战；第3节回顾现有FPGA布局布线算法的优劣；第4节详细介绍OpenPARF算法框架；第5节通过实验验证框架的性能和效率；第6节对本文进行总结，并展望未来的研究方向。

2 研究背景

2.1 FPGA架构简介

FPGA是一种可编程逻辑芯片，其逻辑电路结构可以被动态配置，从而在实现不同的功能或应用时提供更大的灵活性和可定制性。不同厂商制造的FPGA芯片架构大体相同，局部硬件配置上有少许差异。图1抽象出了FPGA的布局布线架构的统一视角。FPGA布局布线架构包括时钟区域(Clock Region)、片(Tile)、片上位置(Site)以及基础逻辑单元(Basic Element of Logic, BEL)。

(1)BEL。BEL是FPGA架构中基本组成单元。BEL可分为逻辑BEL和布线BEL两种类型。逻辑BEL是表示FPGA逻辑功能的最小单元，如查找表(LookUp Table, LUT)和触发器(Flip-Flop, FF)等。布线BEL是一种可编程的布线多选器，用于B E L 之间的连线布线。布线阶段将由F P G A CAD工具配置布线BEL。

(2)Site。Site的组成元素包括：(a) 一组关联的BELs；(b) Site与外部的输入输出引脚(Site Pin)；(c) Site内部的BELs与Site Pins之间的连线。Site的主要类型包括CLB、数字信号处理单元(Digital Signal Processing, DSP)、块存储单元(Block RAM, BRAM)和用于接口的输入/输出块(Input/Output block, IO)等。Site在FPGA版图上呈2维排布，且同类型的Site成列分布。

(3)Tile。Tile由Site以及交换框(Switch Box)组成。Switch Box在FPGA上呈阵列分布，是FPGA上最重要的布线中继点。Swich Box的连线包括Tile内部的Site与Switch Box之间连线和不同Tile的Switch Box之间的连线。CLB, DSP, BRAM等Site首先连接到同一个Tile中临近的Switch Box，再通过横向和纵向的互联轨道连接到另一个Site。这些互联轨道不仅可以连接相邻的Tile，也可以跨Tile连接(跨Tile连接的互联轨道称为倍线)。

(4)Clock Region。FPGA版图被切分成若干个时钟区域。每个时钟区域进一步被切分成时钟半列(Half Column)。时钟区域和时钟半列内的Tile共享一组有限的时钟布线资源，如时钟信号的种类不能超过一定数量。

以上描述阐述了FPGA布局布线的层次结构。在不同Site类型当中，CLB数量最多、分布最广。CLB可以按照配置逻辑分为SLICEL和SLICEM两种异构类型。以SLICEL为例，图1右下角展示了Xilinx Ultrascale+系列[5]的简化内部构造图，其包括8个LUT, 16个FF, 2个时钟信号(CLK0-CLK1)，4个时钟使能信号(CE0-CE3)以及2个置位-复位信号(SR0-SR1)等。根据BEL和时钟控制信号的组合关系，C L B 进一步被划分成8 组B E L 的组合(Group)，每组包括1个LUT以及2个相邻的FF，组合{0,1,2,3}与组合{4,5,6,7}分别被称为半CLB。SLICEM在SLICEL的基础上，增加了额外的逻辑信号，因此除了可被配置为具有逻辑功能的LUT逻辑单元外，还能被配置为具有存储功能的分布存储单元(Distributed RAM, DiRAM)和移位寄存器(SHIFT register, SHIFT)。

图1右下角以UltraScale VU095为例描述了CLB内的信号线。具体而言，(1)半CLB中FF的CLK信号和SR信号相同；(2)半CLB中FF0的CE信号相同，同时半CLB中FF1的CE信号也相同；(3)如果网表内有LUT逻辑单元的输出信号直接连接到FF上，那么LUT逻辑单元和FF打包在同一个组合内，可以有效减少路由线长。

2.2 FPGA布局布线挑战

FPGA高度异构的芯片架构极大增加了FPGA布局布线的难度。从上述FPGA的芯片架构层次划分可以总结出以下FPGA布局布线挑战。

逻辑单元打包(Packing)规则复杂。打包指的是依次将LUT和FF打包为组合、半CLB和CLB，从而最大化可用的物理资源，减少逻辑单元之间的延迟。逻辑单元打包需要遵守组合内、半CLB和CLB内的信号线连接约束[6]。例如，能否将LUT和FF打包到一个CLB取决于LUT和FF之间的连接关系，以及时钟控制信号与FF的连接关系。

资源异构性高。FPGA Site具有多种类型，包括CLB, DSP, BRAM和IO等。这些类型在FPGA的版图上分布不均，在空间上离散，导致在芯片设计阶段期望的逻辑单元空间分布在物理实现时难以保证。例如，深度学习加速器中常用的脉动阵列是一个由处理单元组成的2维阵列，每个处理单元一般需要使用DSP资源。然而，由于DSP资源在FPGA上成列分布，在实现时难以对齐设计的空间需求[7]。

布局布线资源有限。FPGA的物理实现受限于有限的布局资源容量、布线资源容量和时钟布线资源容量。局部过高的布局密度不仅会造成逻辑资源紧张，更会导致布线拥塞[6,8]。对于布线算法本身而言，FPGA Switch Box之间存在倍线连接，导致连线在空间上存在跳跃的情况，增加了拥塞评估的难度。有限的时钟布线资源对FPGA的布局布线提出了离散度更高的优化约束条件。时钟区域和时钟半列对都经过其中的时钟信号的数量和种类有着严格限制[9]，极大增加了布局布线的难度。

3 相关工作

为解决上述挑战，在最近几年关于FPGA布局算法的研究中，除了通常考虑的线长，可布线性等主要优化目标，在布局阶段还加入了时钟信号布线等优化指标，把后续流程的优化目标提前到布局阶段，从而减轻后续优化流程的难度。在关于FPGA布线算法的工作中，提出了加速迭代收敛的布线算法来求解大规模布线资源图上的布线问题。随着布局布线问题规模的不断扩大，也出现了利用异构计算和机器学习[10]来提高FPGA布局布线算法运行效率的研究工作，极大加速了FPGA设计流程的迭代流程和设计周期。

3.1 FPGA布局相关工作简述

目前工业界和学术界使用的布局算法主要使用解析式优化算法，包括比较成熟的基于力学模型的2次规划方法[11]和非线性优化算法[12]。基于2次规划的算法运行迭代次数更少，求解速度更快；相比于非线性优化算法，非线性模型能够对优化目标函数进行更加平滑的近似，布局结果质量相对较优，但是也引入了更高的复杂度。

在最近几年提出的非线性优化算法中，文献[13–16]提出了基于静电场系统的近似全局密度估计函数和基于Nestrov的非线性梯度优化算法，在公开测试数据上获得普遍较好的布局结果。基于静电场系统的布局算法把网表中的逻辑单元建模成带电体，逻辑单元受到彼此之间的斥力作用从而使得逻辑单元密度受到约束；并且目标函数中的密度项对应于静电场系统整体的电势能，逻辑单元受到电场力影响朝着电势能减少的方向移动，等价于在对目标函数进行优化。另外，基于梯度的优化算法能通过并行化算法处理百万级别的网表规模，可以充分使用CPU多线程或者GPU进行并行加速[17–20]。

布线拥塞驱动的FPGA布局算法。 随着设计复杂程度的提升，在布局阶段单纯考虑优化线长可能会导致在后续的布线阶段出现布线拥塞的情况。因此部分研究考虑在布局阶段加入对可布线性的考虑来减轻后续布线阶段的压力。文献[21]和文献[18]提出在布局阶段提前做布线资源使用情况估计，并对处于布线拥塞区域的逻辑单元进行面积膨胀，膨胀后的面积将反映在密度估计函数上，从而减少该区域的布线拥塞程度。文献[22]提出在打包阶段和详细布局阶段使用膨胀后面积来进行匹配从而减少拥塞程度。文献[23]考虑到FPGA相比于专用集成电路 (Application Specific Integrated Circuit, ASIC)布局资源分布不均衡的问题在全局布局的初始阶段进行考虑到布线资源分布的网表分割，并在布线资源估计时加入引脚数量作为权重进行估计。除了基于面积膨胀的算法，文献[24]提出在引脚密度估计中使用基于概率分布的布线拥塞估计算法。对布线拥塞程度进行估计一直是FPGA布局问题中的难点，一个问题是目前主要的布线拥塞的解决算法以静态位置为主，但是在动态调整cell位置的过程中可能会引入了新的布线拥塞区域。

考虑时钟布线的FPGA布局算法。由于FPGA特殊的时钟布线结构，近年来也有一些工作把布局算法的优化方向放在时钟布线的优化上。当前学术界主流算法[23–28]主要对每个时钟信号求出可放置的一组时钟区域，然后通过合法化或者以平滑化方式消除关于粗粒度的时钟区域布线限制，然后在合法化和详细布局阶段完成细粒度的时钟半列限制。文献[26,27]分别提出通过“收缩-扩张”算法和最大流匹配算法求出每个时钟信号可放置的一组构成矩形的时钟区域，文献[17,25,29]则提出在获得每个时钟信号可放置的时钟区域后，通过2次罚函数法把时钟布线加入优化问题的目标函数中，这种算法能以更加平滑化的方式优化时钟布线并获得更好的布局质量。除此以外，文献[28]进行了更加细粒度的初始时钟布线，每个时钟信号可以放置的时钟区域构成联通的多边形，因此该算法更加精细地扩大了时钟布线的可行解空间并能获得更好的布局质量。由于时钟布线限制的高度离散性，当前主要做法为在连续优化过程中加入对时钟信号可行区域的合法化过程，这种使用静态限制的方法压缩了可行解空间。

FPGA布局中的打包算法。打包算法可以分为直接打包、层次打包和非显式打包3类。直接打包首先根据逻辑互连确定打包方案，然后依次进行布局和合法化，以产生合法布局结果。然而，直接打包算法[30,31]在算法决策流程中缺乏逻辑单元的空间信息，因此结果质量较差。层次打包算法[11,22,23]首先生成初始布局结果，然后结合逻辑单元的初始布局信息完成打包，并接着将打包后的逻辑单元视为整体继续进行布局。打包具有组合级、半CLB级和CLB级等层次，可以与布局算法交替进行。层次打包在最终布局和合法化前可以结合逻辑互连和位置信息。非显式打包算法[32]则直接在初始布局结果上完成打包和合法化，非显式打包可以减少初始布局结果和最终布局结果之间的差异。最近，也有部分工作提出使用图神经网络预测逻辑单元的打包概率[33]。

目前，基于非线性优化算法的布局算法普遍能够取得较好的布局效果，并且在可布线性、时钟布线性等下游优化任务以及使用异构计算加速优化算法上也已取得一定进展。然而，仍然存在一些尚待解决的问题。在可布线性优化方面，动态布线拥塞程度仍然是一个难点；由于时钟布线约束的高度离散性，基于连续优化算法的求解空间受到限制，这给求解优化问题带来更大的难度。

3.2 FPGA布线相关工作简述

目前学术界现有的FPGA布线工具主要采用的是协商式的路径搜索算法，其中具有代表性的算法为PathFinder算法[34]。对于每个线网，该算法会为该线网的每个扇出依次寻找一条从扇入到该扇出的布线路径。在寻找到一个扇出的布线路径时，该算法会将该扇出所属线网的已有布线结果全部加入一个优先队列中，然后使用Dijkstra算法或A*算法等常用的路径搜索算法来寻找路径。在这样得到的布线结果中，不同的线网的布线结果之间可能产生拥塞，因而该算法会对拥塞线网迭代地进行拆线(ripup)和重布线(reroute)。在每次迭代开始时，该算法会检查现有的布线结果中是否存在拥塞。对于存在拥塞的线网，该算法会将其布线结果删除，也即相当于将已有的布线结果“拆线”。然后，该算法会提高存在拥塞的布线资源的布线开销，并对存在拥塞的线网进行重布。

缩小搜索范围。在拆线－重布过程中，AIR[35]和CRoute[36]都采用了只对具有拥塞的扇出引脚进行重布的策略，缩小了布线搜索范围，从而提高了布线效率。Zha等人[37]提出了一种重定义的布线开销计算策略，从而减少在特定情况下布线拥塞产生的概率，减少了重布线的次数。AIR[35]中对于扇出较多的线网，会在对一个扇出布线时只将其周围的布线结果加入优先队列中以减少搜索范围。

并行加速布线。不少研究采用并行计算方法加速布线。文献[38]使用GPU等异构并行计算工具对单个线网进行布线。文献[39]对FPGA版图进行特定的划分以同时布线多个线网。一般情况下，并行布线会以降低布线结果质量为代价，换取布线时间的减少。

4 算法描述

OpenPARF的总体算法框架如图2所示。该算法以电路网表和FPGA布局布线架构信息为输入，能够自动输出完整的布局布线结果。整个流程包括布局阶段和布线阶段两个阶段，具备SLICELSLICEM建模、布线拥塞预测和时钟布线优化的功能。OpenPARF可以支持工业级FPGA设计中常用的逻辑单元库，包括LUT, FF, DSP, BRAM, IO以及具有SLICEL-SLICEM异构性质的DiRAM和SHIFT。考虑到IO在FPGA芯片上的位置通常已经固定，因此在布局阶段只需考虑剩下的逻辑单元类型S={LUT, FF, DSP, BRAM, DiRAM, SHIFT}。在接下来的章节中，将对OpenPARF布局布线框架的主要功能进行详细介绍。

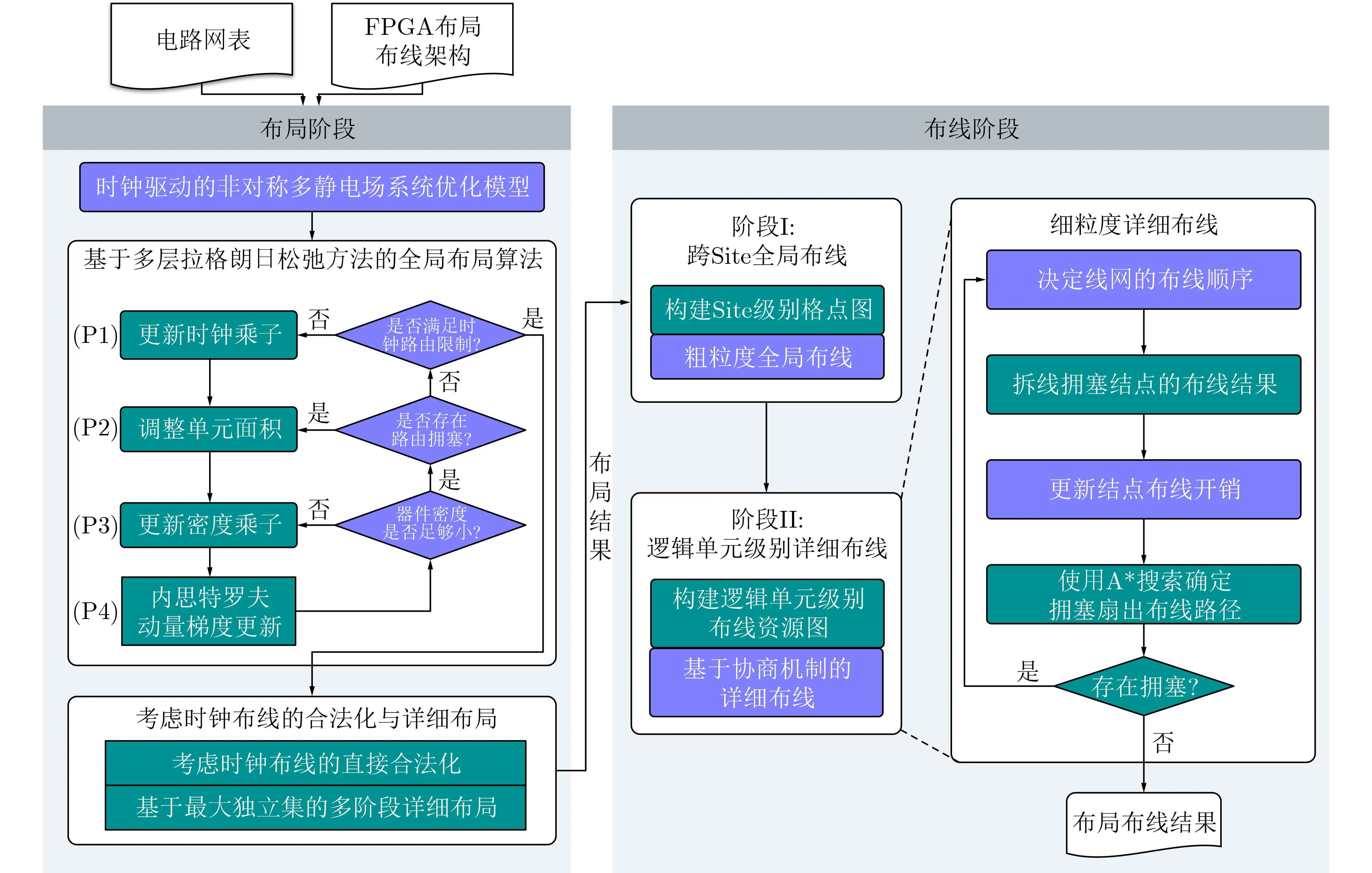
图2 OpenPARF 总体算法框架图

4.1 布局阶段

根据FPGA的布局架构和电路网表，本文提出一个基于非对称多静电场系统的FPGA布局器。在布局问题中，电路网表可以用超图H=(V,E)表示，其中V表示所有逻辑单元组成的集合，E表示所有线网组成的集合，所有逻辑单元的横纵坐标用向量x和y表示。首先，布局器通过全局布局步骤同时优化非线性目标函数中的线长、非线性密度分布、布线拥塞以及时钟布线等多个目标。然后，合法化步骤生成符合时钟布线约束和FPGA设计规则的合法布局结果。最后，OpenPARF在详细布局阶段微调逻辑单元的位置，以进一步优化线长。

4.1.1 基于多层拉格朗日松弛方法的全局布局算法

OpenPARF类似文献[17,18]使用了非线性全局布局算法，同时考虑了线长、逻辑单元的分布密度、布线拥塞程度和时钟可布线性等因素。具体而言，OpenPARF将全局布局问题建模为如式(1)的带约束优化问题

其中，OpenPARF采用了线长优化目标W(x;y)来优化电路布线结果。线长优化目标被定义为所有线网的半周长线长(Half-Parimeter WireLength,HPWL)[40]之和。HPWL提供了路由线长的估计下限，在布局阶段被广泛用于估计路由线长。具体而言，线网的HPWL是由其所有引脚垂直/水平坐标的最大值和最小值之差决定的。OpenPARF采用了WA(Weighted Average)模型[40]得到线长优化目标中的最大值和最小值函数的近似可导形式。这种近似可导形式的最大值和最小值函数使得目标函数的导数可以使用标准的数值优化方法来计算，从而加速了优化过程。

在OpenPARF中，Φt(x;y;At)表示静电场系统t(t ∈T) 的 电势能，其定义类似于文献[17]，T集合包括静电场系统的所有类型。本文使用了非对称的多电场模型来建模SLICEL-SLICEM的异构性(见4.1.2节)。静电场系统将逻辑单元建模为带电体，逻辑单元的重叠会导致静电场的电势能增加。优化目标是要尽可能降低电势能，以减少逻辑单元之间的重叠程度，避免布线过于拥挤。通过最小化静电场系统的电势能，可以有效地避免逻辑单元之间的重叠，从而改善电路布线的质量。

Γ(x;y)表示时钟布线约束惩罚项(见4.1.3节)。当没有违反时钟布线限制时，惩罚项的值为零。当违反时钟布线限制时，惩罚项的值会增加。优化目标是尽可能减少惩罚项，将逻辑单元导向合法区域，并最终消除时钟布线违规的情况。

上述约束条件体现了FPGA布局的物理限制，包括电路板的大小和形状、标准单元之间的间距、布线拥塞程度和可时钟路线性等因素。通过对目标函数的优化，OpenPARF可以同时考虑这些因素，从而得到更优的布线结果。为了求解上述带约束优化问题，OpenPARF引入了无约束增广拉格朗日函数L(x,y;λ,A,η)，其具体形式为

其中，Dt表 示类型t静电场系统的拉格朗日项，包括其电势能Φt的 1阶项和2阶项；ct用 于平衡Φt的1阶项和2阶项的大小；λt表示Dt的拉格朗日密度乘子；η表示拉格朗日时钟乘子。

如式(3)和图2所示，OpenPARF采用多层拉格朗日松弛方法求解拉格朗日函数的最优化问题。该优化框架从外向里依次优化时钟布线、布线拥塞、分布密度和线长。从整个优化过程来看，这3个约束在嵌套的优化迭代中逐渐增强。当优化过程完全收敛时，全局布局阶段结束。对于时钟和分布密度约束，OpenPARF引入了对应的拉格朗日乘子η和λ，增加它们的值可以分别加强时钟布线和密度限制

具体而言，在该多层拉格朗日松弛方法的优化框架中，

(P1)首先，OpenPARF判断是否满足时钟布线约束。如果未满足时钟布线约束，则更新时钟乘子。OpenPARF利用时钟布线分配算法更新时钟罚函数项，同时增大时钟乘子，增强时钟布线约束限制，以使其符合布局布线架构的要求。

(P2)其次，OpenPARF判断是否存在布线拥塞问题。如果存在布线拥塞，则采用类似于文献[20]的方法缓解路由拥塞。OpenPARF通过逻辑单元密度和RUDY算法[41]估计布线拥塞程度。如果当前布线拥塞程度超过阈值，则调整逻辑单元面积(等效于调整电场模型中逻辑单元所带的电荷量)，缓解布线拥塞问题，并增强可布线性限制。

(P3)接着，OpenPARF判断逻辑单元密度是否小于给定的阈值。如果逻辑单元密度大于阈值，则增大密度乘子，增强对密度分布约束的限制，分散逻辑单元。

(P4)经过上述步骤，时钟可布线性、路由拥塞和逻辑单元重叠等问题都得到了良好的解决。Open-PARF使用内思特罗夫动量法优化线长，直到优化问题完全收敛。最终，OpenPARF得到满足时钟布线约束、路由拥塞程度以及器件分布密度优化的全局布局结果。

4.1.2 SLICEL-SCLIEM异构性非对称多电场模型

2.1节讨论了SLCEL中的LUT资源可以被配置为LUT逻辑单元，SLICEM中的LUT资源可以分为LUT, DiRAM和SHIFT逻辑单元。由于SLICEL和SCLIEM具有不同的布局布线规则，在布局中要同时考虑这两种Site之间的相互作用。OpenPARF采用了类似于文献[17]的非对称多电场模型，在多电场系统中引入了LUTL和LUTM-AL两组静电场系统。这两组静电场系统的设置目的是避免DiRAM或SHIFT逻辑单元被映射到SLCEL上，同时允许LUT逻辑单元放置到SLCEL和SLICEM上。

LUTL静电场系统模拟SLCEL和SLICEM中提供的逻辑LUT资源，而LUTM-AL模拟SLICEM上提供的与存储功能相关且在SLICEL上不存在的逻辑资源。与此对应，逻辑单元LUT只占用LUTL静电场系统中的资源，而逻辑单元DiRAM和SHIFT则同时占用LUTL和LUTM-AL静电场系统中的资源。

图3以LUT和SHIFT逻辑单元为例，分析了4个场景下两者的位置关系。DiRAM逻辑单元的布局规则与SHIFT逻辑单元类似。由于SLCEL不包含LUTM-AL的资源，其初始LUTM-AL密度设置为1，表示它已被占用；LUTL的初始密度设置为0，表示在SLCEL上LUTL资源还没有被占用。同样地，由于SLICEM同时拥有LUTL和LUTM-AL资源，因此它们的初始密度都设置为0。在场景I和II中，LUT逻辑单元分别放置在SLICEL和SLICEM上，两个静电场系统中都没有发生密度溢出，这意味着电势能达到了最小值。场景III和IV中，SHIFT逻辑单元放置在SLICEL上，LUTM-AL静电场系统发生密度溢出，表示静电场系统的电势能较高。优化器通过最小化势能来避免发生这样的情况。这样，这两个静电场系统可以自然引导LUT和DiRAM/SHIFT逻辑单元放置到合法的Site中。

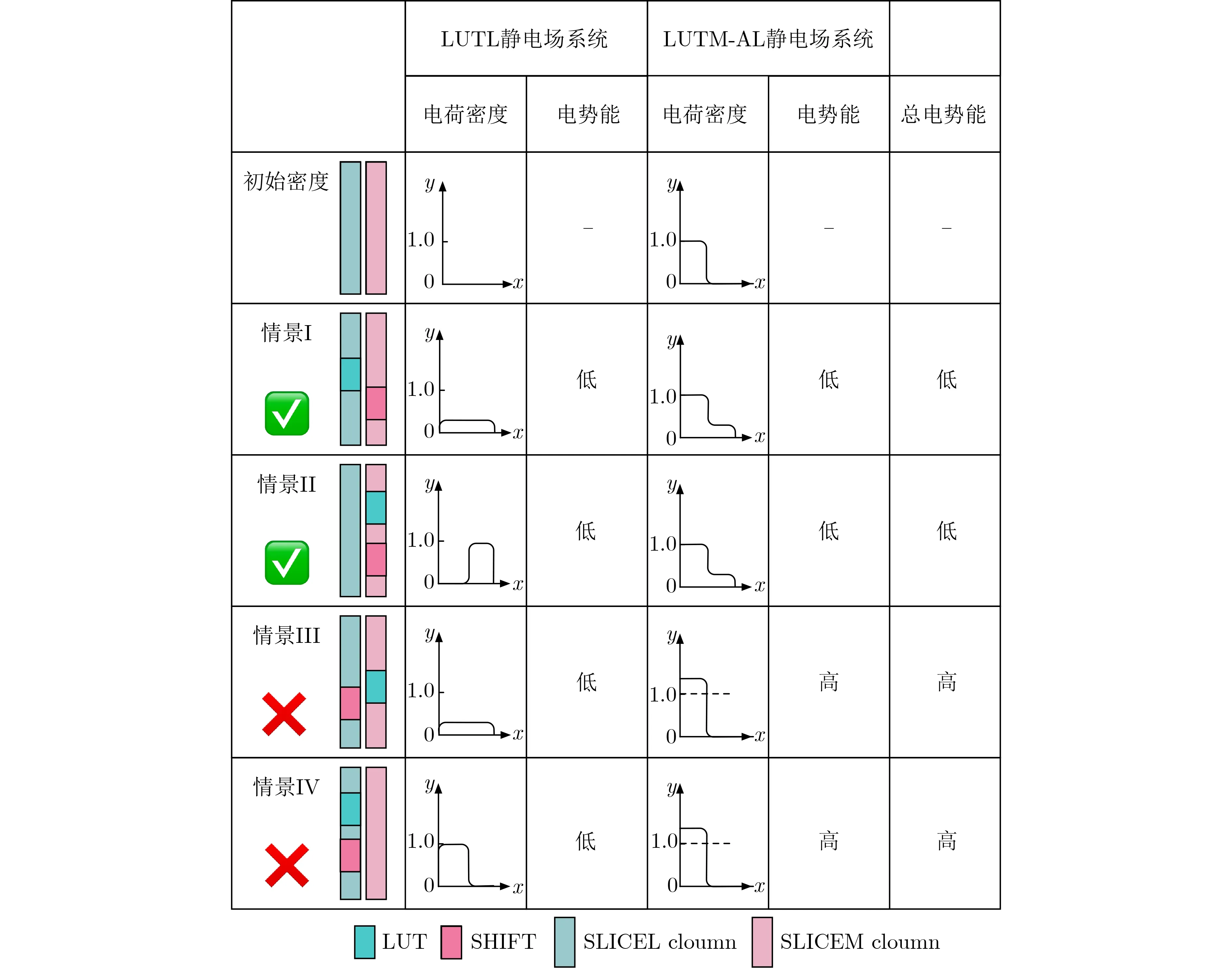
图3 4 种情景下的 LUT 和 SHIFT 的位置关系下 LUTL 和 LUTM-AL 静电场系统的电荷密度和电势能

4.1.3 2次罚函数时钟惩罚项模型

OpenPARF采用文献[27]中的算法来生成逻辑单元到可用时钟区域的映射。这种方法保证了生成的映射不仅符合时钟布线限制，还可以降低线长扰动。这些映射被用来确定逻辑单元与可用时钟区域之间的关系。在该映射的基础上，OpenPARF定义了增广拉格朗日函数中的时钟布线约束惩罚项Γ(x,y)，该惩罚项的值等于所有逻辑单元时钟布线约束惩罚项之和。假设逻辑单元i可用的时钟区域集合为wt， 且wt的边界框的左部、右部、底部和顶部边界坐标分别为： loxi,h ixi,l oxi和h iyi。逻辑单元i的时钟布线约束惩罚项等于x轴方向和y轴方向的惩罚项之和

其中，x轴方向上惩罚项Γ(xi,yi)x为

xi和yi为 器件i的横纵坐标，y轴方向上的时钟惩罚定义类似。逻辑单元i的时钟布线约束惩罚项是一个以合法区域为中心的2次势阱函数。当逻辑单元在合法区域中时，惩罚项为零。否则，惩罚项的值会增加，并在梯度更新过程中将逻辑单元导向合法区域，这样就可以消除时钟布线违规的情况。

4.1.4 考虑时钟布线的合法化与详细布局

在全局布局阶段后，OpenPARF对全局布局结果执行合法化步骤来获得一个没有标准单元重叠、满足FPGA布局布线架构规则且路由拥塞程度得到优化的布局结果，并在此步骤中尽可能减少对全局布局结果的扰动。在这个步骤中，OpenPARF类似于文献[32]进行初步合法化，接着采用并行college-student Admission策略更新逻辑单元的组合关系，最后得到合法的布局结果。

最后，在详细布局阶段，OpenPARF采用基于最大独立集的匹配算法[32]，在合法化的结果基础上微调逻辑单元的位置，以进一步优化线长。在这个阶段中，布局器会生成遵守FPGA布局布线架构规则和时钟布线约束的详细布局结果。

4.2 布线阶段

在布线阶段，OpenPARF提出了一个BEL级别的两阶段布线器[39]。布线器以布局阶段的结果和FPGA布线架构作为输入，生成最终的布线结果。该布线器主要包含全局布线和详细布线两个阶段。在全局布线阶段，布线器生成跨Tile级别的粗粒度布线结果，用于指导详细布线。在详细布线阶段，布线器以粗粒度布线结果作为布线区域引导，生成BEL级别的最终布线结果。

在进行全局布线和详细布线的过程中，布线器借助布线资源图(Routing Resourse Graph, RRG)建模FPGA的布线架构。RRG是一幅有向图G(V,E)。 其中结点v∈V表示FPGA中的一个布线资源，并且在全局布线阶段和详细布线阶段分别表示不同粒度的布线资源；有向边(u,v)∈E表示FPGA中的路由通道，表示逻辑信号可以从布线资源u传输到布线资源v。

布线器的核心是基于协商式的PathFinder算法[34]。算法迭代应用A*路径搜索算法，得到合法的布线结果。在每次迭代开始时，布线器检查上一次迭代的布线结果。对存在拥塞的布线资源，布线器提高其布线开销，同时拆除占用该布线资源的线网布线结果。在全局布线阶段和详细布线阶段，Open-PARF采用了不同的开销评估函数来评估布线资源的布线开销。

4.2.1 全局布线

在全局布线阶段，布线器的目标是生成跨Tile级别的粗粒度布线结果，用于指导详细布线。大部分来自学术界的FPGA布线器直接生成详细布线结果。相较而言，OpenPARF加入了全局布线的步骤，以减少在详细布线中可能出现的拥塞问题。在没有全局布线结果的指导下进行详细布线会导致大量的拥塞，进而降低了布线器在求解时的效率。随着FPGA布线架构复杂度的提升，这种情况尤其显著。

全局布线中开销评估函数的优化目标是引导线网的走线避开拥塞区域，并为详细布线预留充足的布线资源。OpenPARF将FPGA布线架构建模为一个RRG格点图。在RRG格点图中，结点代表FPGA架构中的Tile；边代表Tile之间的互联轨道，边容量为对应的轨道宽度。边布线开销的初始值为Tile之间的曼哈顿距离。在此RRG格点图中，线网的扇入扇出为其所在的Tile。

在RRG格点图构建完成后，全局布线器使用PathFinder算法来对跨Tile线网进行布线。在路径搜索过程中，全局布线器采用如下的开销评估函数来计算从结点u扩展到结点v的布线开销

其中，p rev(v)表 示已搜索路径的总布线开销；pred(v)表示当前线网从待扩展结点到扇出结点的预测布线开销，其值等于待扩展结点到扇出结点的曼哈顿距离。随着布线的进行，边容量会随着线网对布线资源的占用而逐渐下降。为了避免造成详细布线阶段的拥塞，全局布线器会随着边容量的下降逐步提高边的布线开销。

4.2.2 详细布线

在全局布线结果的指导下，详细布线器的目标是生成BEL级别的布线结果。与全局布线器相比，详细布线器更加关注跨Tile级别的拥塞。在详细布线阶段，OpenPARF将布线架构建模成细粒度的RRG。在该RRG中，结点代表逻辑引脚；边代表逻辑引脚之间的连接关系。通常情况下，每个逻辑引脚只能用于布线一个线网，因此大多数结点和边的容量都为1。同时由于每个线网的扇入和扇出都是一个逻辑引脚，因此可以很容易地在RRG中找到对应的结点。

详细布线器的目标是为每个线网找到一条从扇入结点到扇出结点的布线路径，并避免拥塞情况的发生。详细布线器与全局布线器均基于PathFinder算法，但由于详细布线阶段的RRG规模更大、连接关系更复杂，OpenPARF采用(1)拥塞驱动布线开销计算、(2)引脚融合与交换、(3)搜索空间大小控制和(4)拥塞驱动布线排序策略来优化详细布线器。

拥塞驱动布线开销计算。详细布线器采用以下拥塞驱动的开销评估函数来计算从结点u扩展到结点v的布线开销

其中，参数p在每次迭代都会乘以预先设定好的参数pc。参数p越大，详细布线器就会更专注于解决布线时产生的拥塞。

o(v)表 示当前结点v被使用后，其容量会超出多少。

b(v)代 表结点v的基础布线开销。对于大多数结点来说，它们的基础开销是相同的。但是，在构造RRG时，对于一些可能产生拥塞的结点，详细布线器会提高其基础开销以在一定程度上避免拥塞的发生。

h(v)代表结点的历史拥塞开销。在迭代拆线过程中，详细布线器根据结点的历史拥塞情况提高其历史拥塞开销。

w(u,v)代表边布线开销，其由边类型决定。Tile内部的边布线开销在构造RRG时会被固定初始化；跨Tile的边布线开销初始化为Tile之间的曼哈顿距离。

引脚融合与交换。LUT是FPGA架构中最常见的逻辑单元。LUT通常是多输入/输出引脚的，然而这些引脚是逻辑不等价，因此连接到这些引脚的互联轨道也是不等价的，这会使得布线器更难找到合法的布线结果。OpenPARF采取了“融合-交换”策略来处理该问题。具体而言，在布线时，Open-PARF将这些引脚合并为一个容量更大的节点，然后在引脚融合后的RRG上进行详细布线。然而，这样做可能会改变线网信号连接的引脚，导致逻辑功能不正确。因此在完成详细布线后，Open-PARF再进行CLB级别的引脚交换(等价于重新设计LUT的真值表)来修正逻辑功能，从而确保了LUT逻辑功能的正确性。

搜索空间大小控制。OpenPARF基本上以全局布线结果为指导进行搜索，在搜索线网路径时只会搜索处于全局布线结果范围内的结点。这种方法可以有效控制搜索空间，加速布线进程。但是，仅在全局布线结果范围内的搜索可能无法消除局部拥塞。因此，每经过若干轮迭代，详细布线器在拆解拥塞结点所在的布线路径时，将该拥塞结点周围的Tile添加到搜索空间中。通过适度增加搜索空间，详细布线器可以更快地找到合法的布线路径。

布线顺序。在每次迭代开始之前，详细布线器需要确定线网的布线顺序。OpenPARF优先对覆盖面积大且在之前布线过程中产生了大量拥塞的线网进行布线，从而更快地消除布线拥塞。

5 实验设置与结果分析

OpenPARF基于pybind11实现C++/Python混合开发，结合了Python的灵活性和C++的高效性。在深度学习框架PyTorch的基础上，Open-PARF对全局布局的梯度计算进行了GPU加速[17]。在实现过程中，本文基于PyTorch的GPU张量管理功能实现了GPU内存管理、快速张量运算和自定义运算算子。此外，本文还利用PyTorch的自动求导功能实现了GPU加速的梯度计算。关于线长和密度模型的具体计算和实现细节请参考文献[17, 20]。本文在一台配备Intel Xeon Gold 6230 CPU(频率2.10 GHz, 40核)、512 GB内存和一块NVIDIA RTX 2080Ti GPU的Linux服务器上进行了实验，并在3个数据集上进行了验证，包括ISPD 2016 FPGA可布线性驱动FPGA布局数据集[6]、ISPD 2017时钟布线驱动FPGA布局数据集[9]和工业标准级FPGA数据集。其中，工业标准级FPGA数据集由工业界的合作方提供，并在其指导下，补全了前两个ISPD竞赛数据集的布线架构。表1和表2详细介绍了这3个数据集的逻辑单元库和电路网表的规模。数据集包括21k～1 100k的不同规模的实例数量和网表大小。

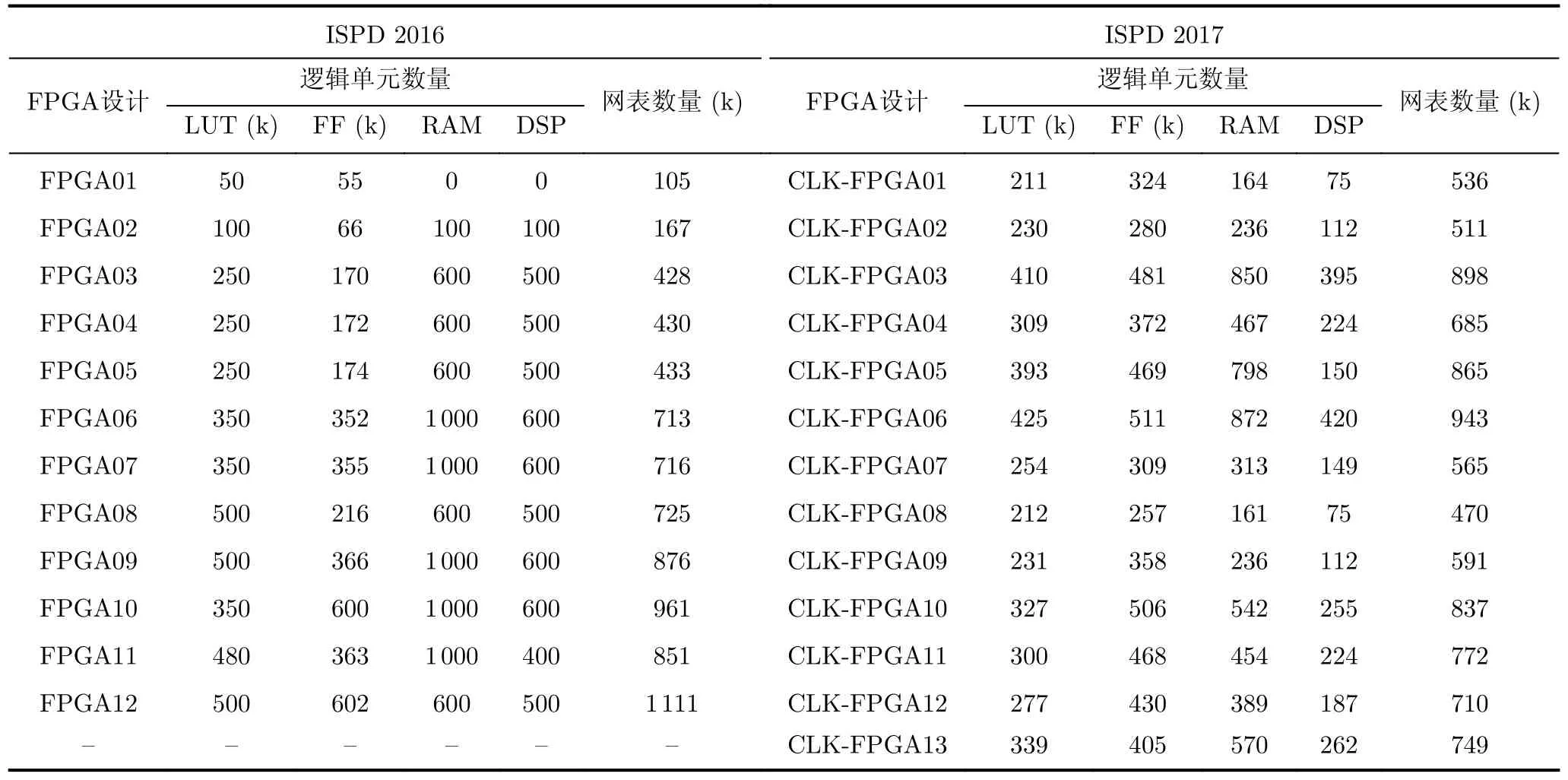
表1 ISPD2016 和 ISPD2017 benchmark 的实例数量和网表数量

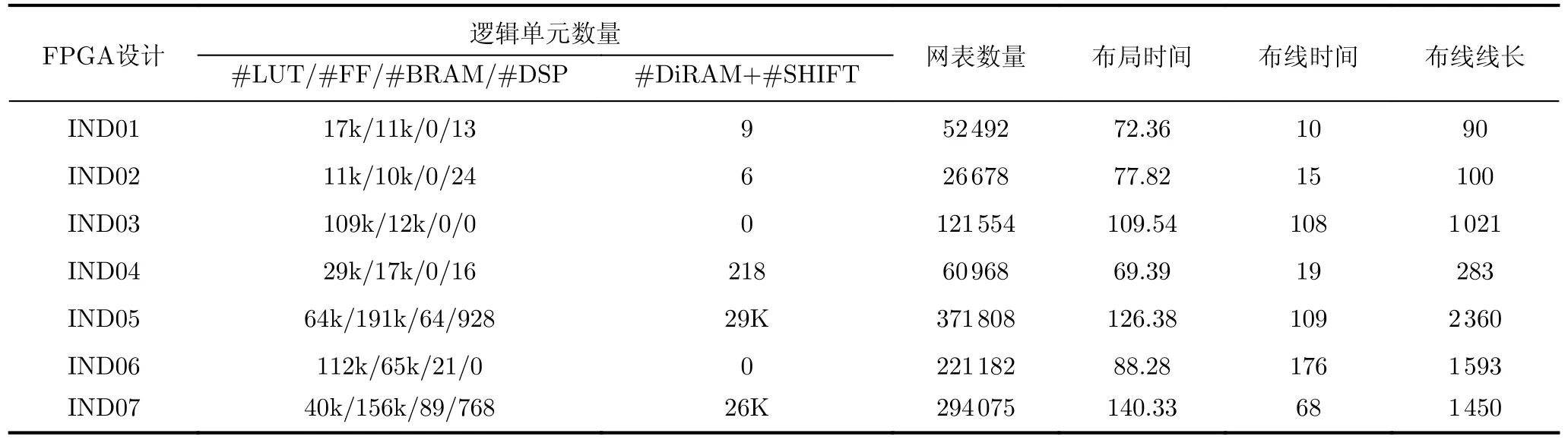
表2 在工业标准级 FPGA 数据集上的布局时间 (s)、布线时间(min)以及布线线长 (×103)

5.1 ISPD竞赛数据集实验结果

表3和表4展示了OpenPARF与其他布局算法RippleFPGA[23]和DREAMPlaceFPGA[19]的对比结果。其中，RippleFPGA和DREAMPlaceFPGA1)DREAMPlaceFPGA包括文献[18,19]两个工作，其中文献[19]在文献[18]的基础上使用GPU加速合法化算法。本文实验部分中DREAMPlaceFPGA的布局时间摘取自文献[19]。分别代表了基于二次规划和非凸优化模型的效果最好的解析式布局算法。本文将其他布局算法的布局结果导入OpenPARF的布线器中进行布线，并比较了布线后线长和运行时间。

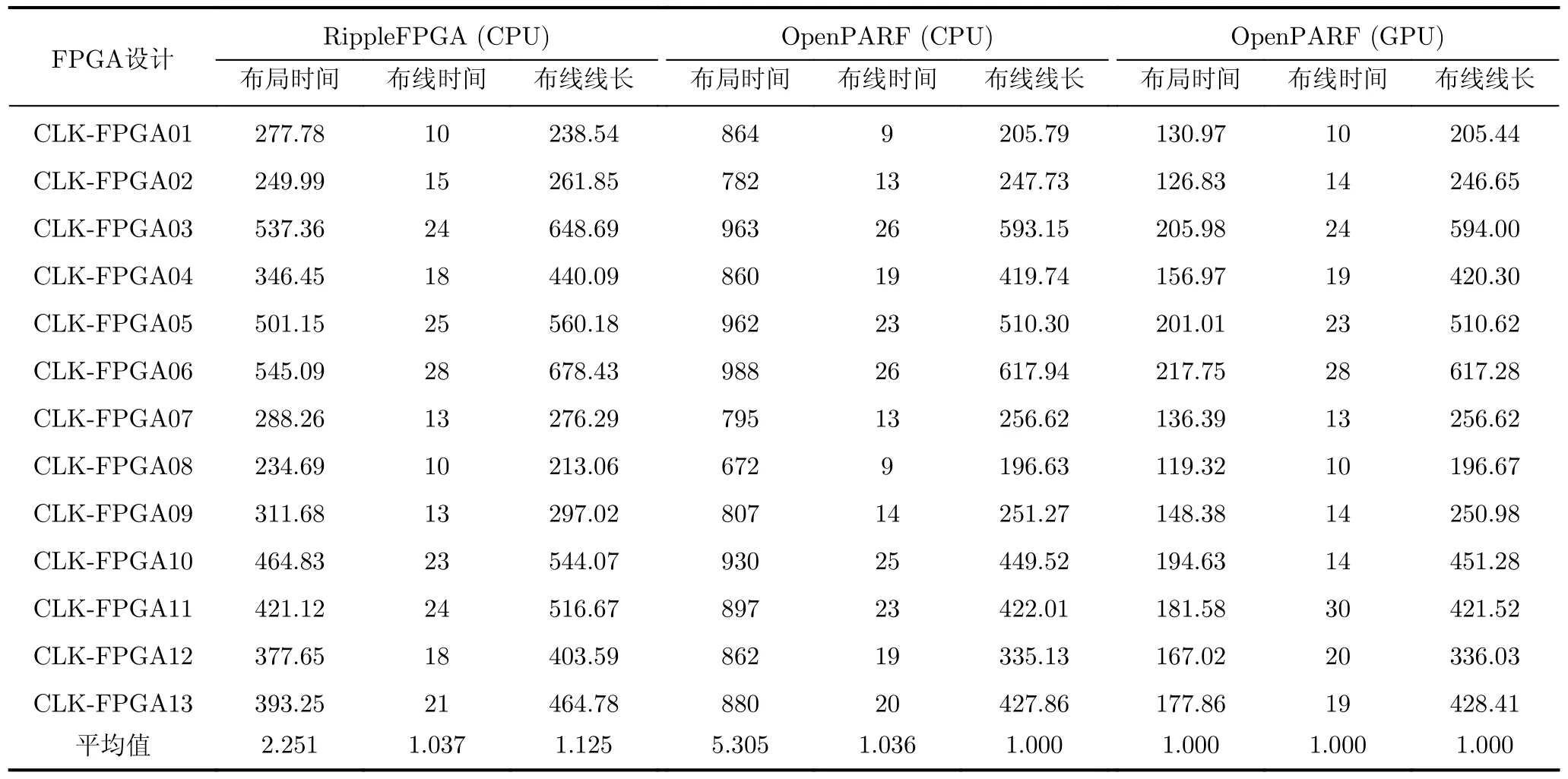
表4 在ISPD 2017 benchmark上的布局时间 (s) 、布线时间 (min)以及布线线长 (×104 )的比较

ISPD 2016上的实验结果表明，OpenPARF相较于其他布局算法，分别减少了12.7%和0.4%的线长，并获得了2.771倍的加速。DREAMPlaceFPGA对合法化进行了GPU加速优化。与DREAMPlace-FPGA相比，OpenPARF慢了21.4%。本文认为，OpenPARF未来可以通过探索使用异构并行加速合法化和详细布局来进一步提高性能。

在ISPD2017数据集上，本文对比了RippleFPGA与OpenPARF的布局布线时间和布线线长。由于DREAMPlaceFPGA目前不支持ISPD2017的时钟布线约束，因此无法在该数据集上比较结果。实验结果表明，相比RippleFPGA, OpenPARF减少了12.5%的布线线长，并获得了2.251倍的加速。该实验进一步证明本框架在复杂约束下仍能实现更优秀的布线结果。

本文进一步在ISPD2016和ISPD2017数据集上比较使用CPU多线程加速2)本文实验中线程数为8(OpenPARF(CPU))和GPU加速(OpenPARF(GPU))的实验结果。在ISPD2016和ISPD2017数据集上，OpenPARF(CPU)和OpenPARF(GPU)均得到相近的路由线长。但与此同时，OpenPARF(CPU)的布局时间大于使用CPU的RippleFPGA。这主要是因为，Open-PARF使用基于非线性优化算法的布局算法，其计算量大于使用基于2次规划算法的RippleFPGA。

本文进一步比较了各工作布局结果的布线时间，以衡量布局结果的布线拥塞程度。表3和表4的实验结果表明， OpenPARF在ISPD2016和ISPD-2017数据集上的布线时间分别比RippleFPGA减少了12.7%和3.7%，并且布线时间与DREAMPlace-FPGA相当。这说明OpenPARF在获得更优布线线长的同时，布线拥塞程度远小于RippleFPGA，并与学术界领先的布局算法DREAMPlaceFPGA持平。这一结果证明了OpenPARF在可布线性优化能力方面的卓越表现。

5.2 工业级FPGA数据集实验结果

表2展示了OpenPARF在工业标准级FPGA数据集上的布局布线时间和布线线长。工业标准级FPGA数据集包括具有SLICEL-SLICEM异构性质的DiRAM和SHIFT逻辑单元。实验结果表明，OpenPARF在处理SLICEL-SLICEM约束时表现出优秀的性能和效率。SLICEL和SLICEM作为FPGA中两种不同的Site，由于其具有不同的物理结构和电学性质，在设计中要同时考虑这两种Site之间的相互作用。OpenPARF通过非对称多电场系统建模处理该问题，取得了积极的成效。

6 结束语

本文提出一个面向大规模FPGA的开源布局布线框架OpenPARF。本框架基于深度学习工具包PyTorch实现，支持CPU平台运行和GPU加速。本框架在布局和布线算法方面采用了新型非对称多电场系统和多阶段优化策略，以应对FPGA复杂的布局布线架构和逻辑单元引脚不等价等场景。在布局阶段，OpenPARF将时钟布线、可布线性、密度分布和线长优化统一建模为拉格朗日优化问题，并使用内斯特罗夫动量法求解。在布线阶段，框架提出了全局布线和详细布线两阶段策略，并采用了多种优化方法提升布线器效率，从而实现逻辑单元级别的布线。OpenPARF为下一代高性能FPGA布局布线算法的探索和开发提供了一个重要的基准。未来，将进一步考虑优化布局布线过程中的拥塞和时序性能，并针对FPGA的规整布局布线结构研究更加准确的线长估计方法。