非平整基底上含表面活性剂液滴铺展中的指进现象与分形特性

郭馨声， 李春曦， 苏浩哲， 叶学民

(1.华北电力大学 能源动力与机构工程学院，河北 保定 071003；2. 河北省低碳高效发电技术重点实验室(华北电力大学)，河北 保定 071003)

0 引 言

在有预置液膜的基底上放置含表面活性剂的液滴,因表面上活性剂浓度不同将产生表面张力梯度差,进而驱使液体从低表面张力位置向高表面张力位置移动,即Marangoni效应,Marangoni效应广泛应用于农学、医学及石油开采等方面[1-3]。在此过程中,受扰动因素影响导致铺展过程出现不稳定性,形成指进现象,由此对诸如印刷和镀层品质及散热性能等方面产生不同的影响[3-5],因此对其开展深入研究具有重要的实际意义。

对于液滴铺展过程中出现的不稳定现象,Marmur和Lelah[6]在1981年首次发现了指进现象,随后Troian等[7]在1990年指出Maragoni效应是产生该不稳定现象的重要原因之一,自此大量学者分别研究了分离压、Marangoni力、表面活性剂浓度和种类等对超薄液膜区中指进现象的影响。其中,Warner等[8]通过考虑Marangoni力、表面扩散、毛细作用和范德华力等影响,研究了含表面活性剂液滴铺展的线性和非线性稳定性。Craster和Matar[9]采用数值模拟方法对比了在临界胶束浓度附近表面活性剂诱导的指进现象,指出在中低活性剂浓度下,指进现象演化过程并不明显。

在实验方面,Cachile和Cazabat[10]观察了预置液膜上的指进现象,指出预置薄膜太厚将导致范德华力影响作用较小。Afsar-Siddiqui等[11]在2003年研究了含AOT和SDS表面活性剂的液滴在预置液膜上的指状铺展现象,发现手指的波长与h02/3成正比,其中h0为初始液膜厚度。Hamraoui 等[12]在2004年实验研究中将不同浓度的非离子表面活性剂C12E10和C12E4加在不同纳米级别厚度的预置液膜上进行液滴铺展实验,讨论了活性剂浓度对液膜铺展的影响。Mollaei和Darooneh[13]有关含表面活性剂液滴在预置液膜上铺展的实验发现液滴铺展过程中会出现扩散、收缩和停留三个过程。Sinz等[14]研究了表面活性液体在液体薄膜上的扩散动力学,指出Marangoni力使表面活性剂液滴周围的液膜变薄,并利用荧光显微镜和光学干涉法监测表面活性剂液滴附近和远离液滴的形态。

对于非平整基底上的液膜稳定性,Kalliadasis等[15]模拟了在外力作用下,粘性薄膜流经非平整基底 (沟槽或凸起)的缓慢运动,指出毛细压力的变化将诱发铺展表面出现凹陷或凸起现象。李春曦等[16,17]针对波纹基底上含不溶性活性剂液滴的铺展历程,探讨了非模态稳定性理论下液滴铺展的稳定性及相关参数的影响。王媛媛等[18,19]基于润滑理论和数值模拟了不同初始条件下含活性剂液滴在预置液膜上铺展过程中形成的指进现象的指进特性,利用分形维数分析了指进现象的非线性特征。李永康[20]模拟了受热倾斜壁面上液滴的“爬坡”特性,并指出随温度梯度的增加液滴呈现先“下坡”后“爬坡”的过程。

综上所述,目前液滴铺展过程中有关指进现象的研究主要关注平整基底,而非平整基底对铺展不稳定现象的研究尚待深入。而且与指进现象的相关实验发现手指分裂和屏蔽现象,但目前仍不清楚其演化机理。由于具有微结构的非平整基底对微尺度下的流动具有显著影响[21-23],所以在机械制造领域,许多研究围绕材料表面的微观几何形貌对液膜形成的影响而展开,其中表面附有方槽型和圆槽型基底尤为重要[24-26]。但已有研究尚不能准确区别不同基底形貌对指进现象的影响,特别是在基底形貌与基底粗糙度共同作用下对手指演化过程的联合影响。为此,本文针对多种非平整基底和粗糙度,开展活性剂液滴铺展过程中指进现象研究,分析指进现象中超薄液膜区的液膜厚度、扰动能量、手指的分裂、屏蔽效应和分形特性等典型特征参数,从而揭示指进现象的内在机理。

1 理论模型

1.1 演化方程组

如图1所示,在有预置液膜的凹槽基底上放置含表面活性剂的液滴,受Marangoni效应驱动表面活性剂和内部液体向表面张力较高的区域运动,从而导致液体层变形,在铺展前缘处形成了一种类似阶梯的结构,同时使上游变薄,形成超薄液膜区。

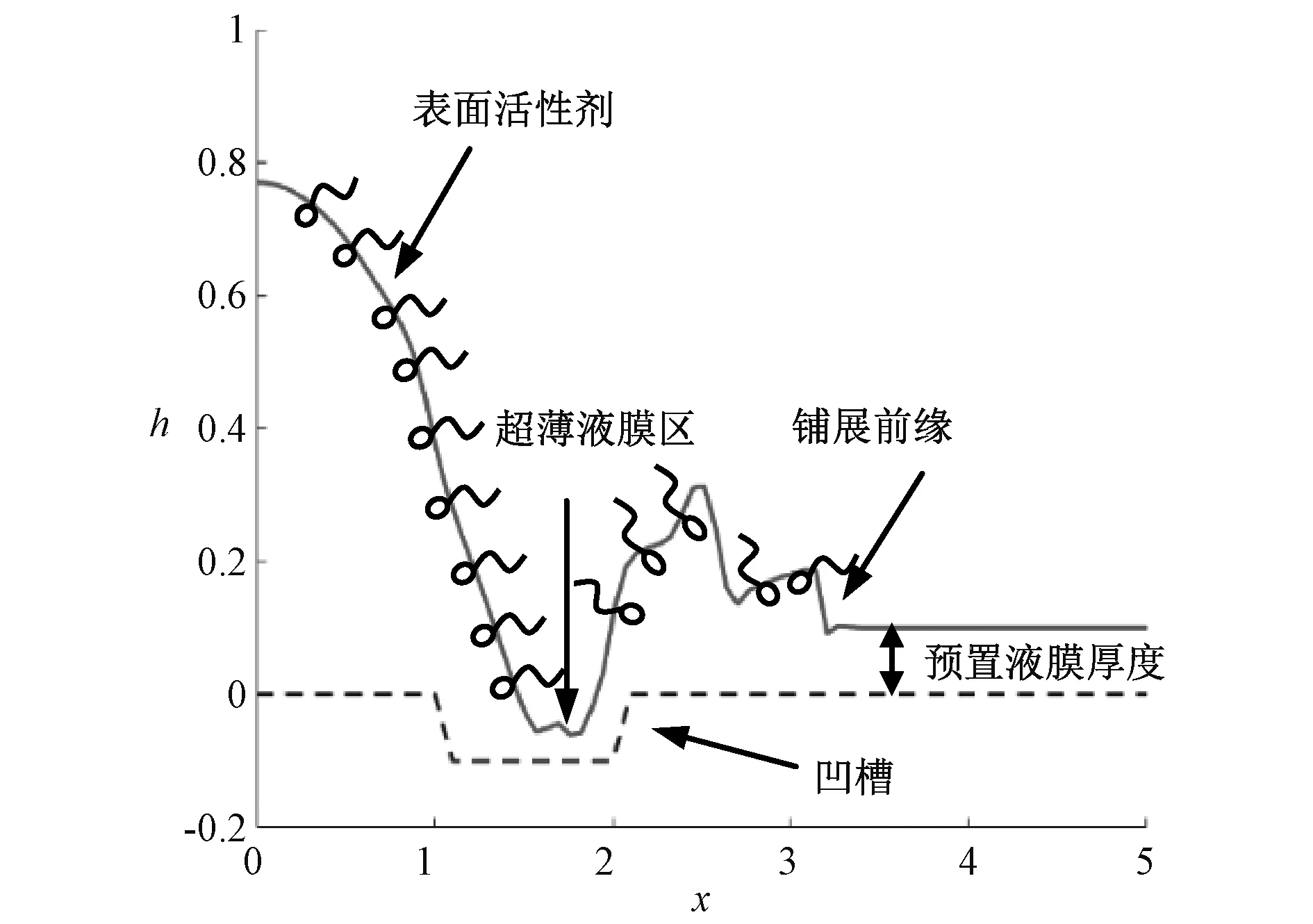
图1 含不溶性活性剂液滴铺展示意图

控制方程组由连续性方程、运动方程和浓度对流扩散方程组成[27]。因液滴初始最大厚度H*与流动方向尺度L*相比非常小,即δ=H*/L*<<1,故可采用润滑理论[28]。

表面张力与浓度间的关系为

(1)

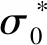
对控制方程组及边界条件进行无量纲化和数量级简化,保留数量级≥O(1),可得液膜厚度h和表面活性剂浓度Γ的演化方程,详见文献[29-31]。

(2)

(3)

式中:C为毛细数;M为Marangoni数;Pe为Peclet数;s为基底形貌函数,下标表示对该变量的偏导。

1.2 基底形貌模

为探究不同形貌基底对超薄液膜区产生的手指现象的影响,下文考虑5种类型基底:平整基底、一维和二维波纹基底、一维和二维凹槽基底,如图2所示。

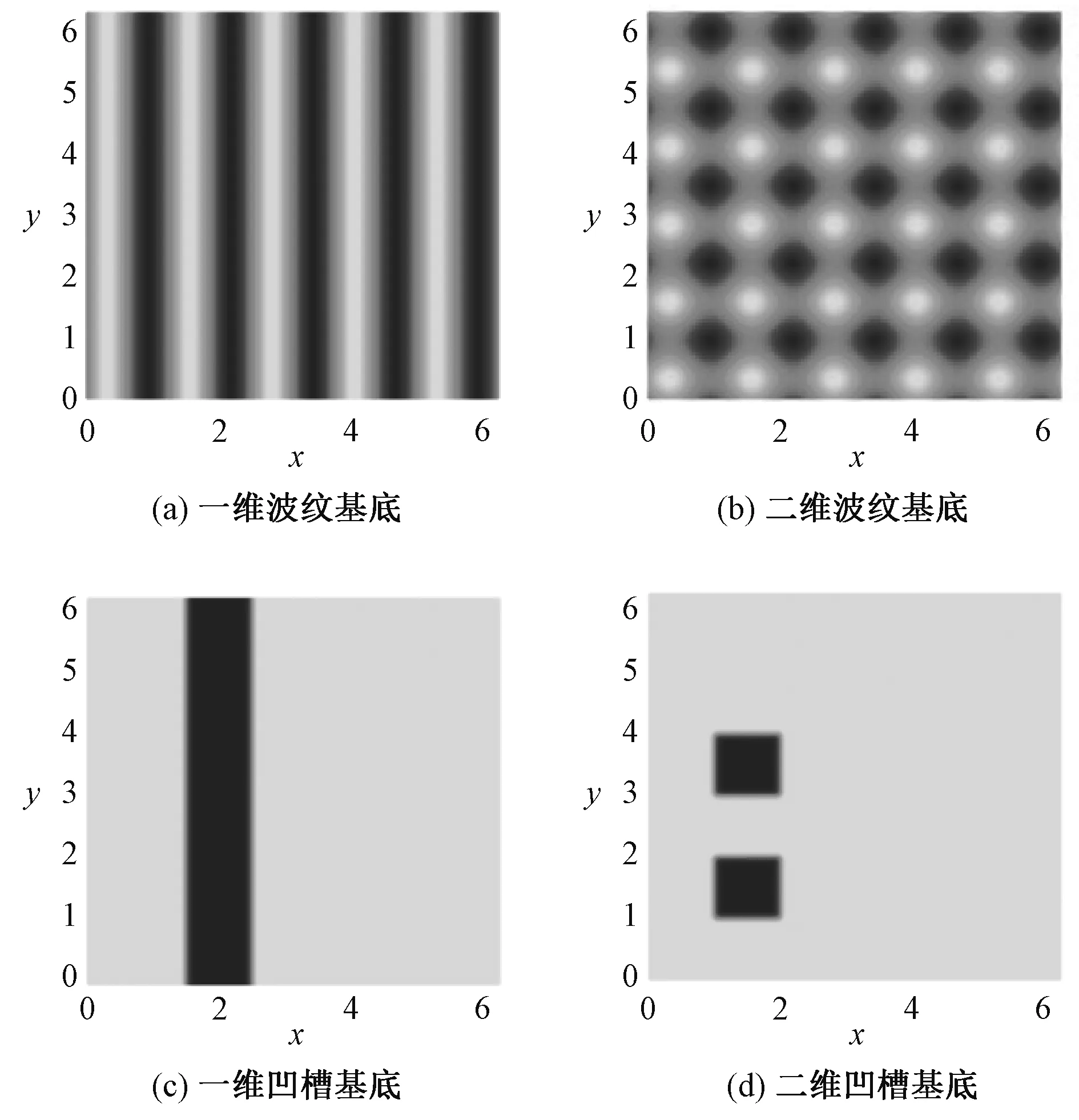
图2 初始时刻基底形态

平整基底为

(4)

一维波纹基底采用正弦函数形式,振幅为0.05,在x方向取5个周期,其表达式为

(5)

二维波纹基底模型在x和y方向均采用正弦函数,其表达式为

(6)

一维凹槽基底形貌表达式为

(7)

二维凹槽基底形貌表达式为

s2n=

(8)

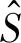
(9)

式中:A为随机扰动的幅值,又称基底粗糙度,本文取0.1和0.5。

1.3 初始和边界条件

假设液滴初始形态与一维波纹基底的剖面如图3(a)所示,初始活性剂浓度如图3(b)所示。

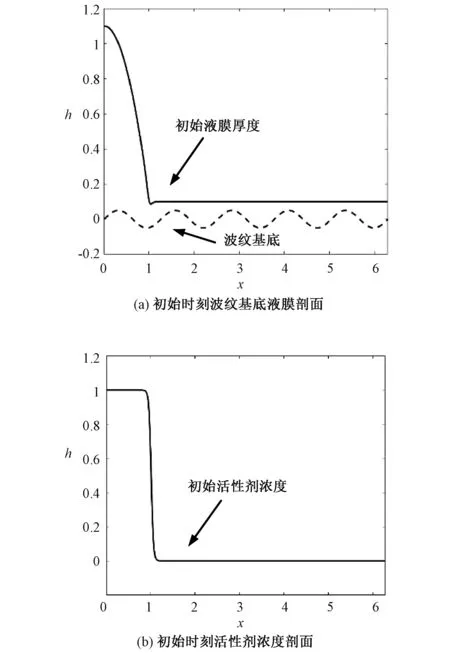
图3 初始条件

液滴初始形状为

h0=(1-x2)H(1-x)+b

(10)

式中:H(1-x)为海氏阶跃函数,表达式为

H(1-x)=0.5×(1+tanh(20(1-x)))

(11)

式中:b=0.1,为无量纲形式的预置液膜厚度。

初始活性剂浓度为

Γ0=H(1-x)

(12)

边界条件:

hx(∞,t)=hxxx(∞,t)=0

(13)

Γ0(∞,t)=0

(14)

2 结果与分析

2.1 指进现象的几何特征

下文通过分析指进现象中的液膜厚度和扰动能量来探究基底形貌与基底粗糙度对指进现象的影响,选取二维波纹与二维凹槽基底为例,t=10、50、90时液膜厚度的空间演化如图4所示。由图4可知,随时间持续,指进现象不断演化,手指逐渐伸长。对比图4(a3)和(b3)可知,基底形貌对指进现象中手指演化过程有显著影响。二维凹槽基底中,每个凹槽两侧形成两根长手指,而凹槽内的手指长度较短、宽度较窄,如图4(a3)放大区域Ⅰ所示。对于二维波纹基底,波峰与波谷之间形成的手指较为明显,且手指在演化过程中指尖处发生了分裂现象,如图4(b2)、(b3)中II和III处所示。

图4 A=0.5时的液膜厚度

2.2 扰动能量分布与液膜厚度

为反映不同基底形貌和粗糙度对液滴铺展的影响,定义扰动为

D=(h(x,y,t)-hb(x,y,t))

(15)

为更清晰地描述扰动的发展,定义扰动能量为

He=(h(x,y,t)-hb(x,y,t))2

(16)

式中:hb为未添加扰动时基态液膜厚度。

利用式(15)和式(16)可得不同基底上的扰动能量分布,如图5所示。该图表明,粗糙度为0.5时,基底形貌对扰动能量的影响更显著,故选择A=0.5时开展分析。对于不同的基底形貌,其扰动能量分布不同:一维凹槽基底的扰动能量集中分布在两侧,中心处的扰动能量微弱;二维凹槽基底凹槽处的扰动能量明显弱于其他处的扰动能量;一维波纹基底在x=1.8、2.2、3.7处,出现较强的扰动能量,且扰动能量随x增加逐渐减弱;而二维波纹基底波峰处的扰动能量几乎为零,波峰与波谷之间的扰动能量则更强。

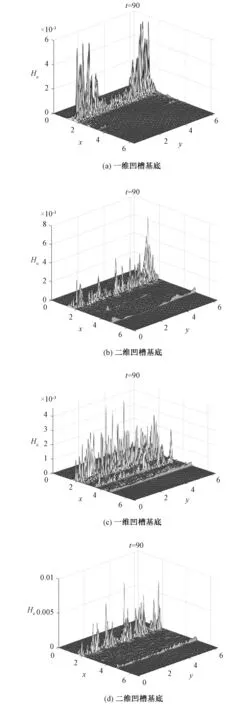
图5 A=0.5时的基底扰动能量分布

为说明扰动能量与超薄液膜区液膜厚度间的关系,图6给出了三种基底形貌下相同y处的液膜厚度截面图。结合图6(c)、6(d)可知,随液膜持续铺展,一维波纹基底上衍生出三处较薄液膜区,液膜厚度h随x增加而变厚,而扰动能量He则随x增加而减弱,由此可知液膜厚度h与扰动能量He成反比。

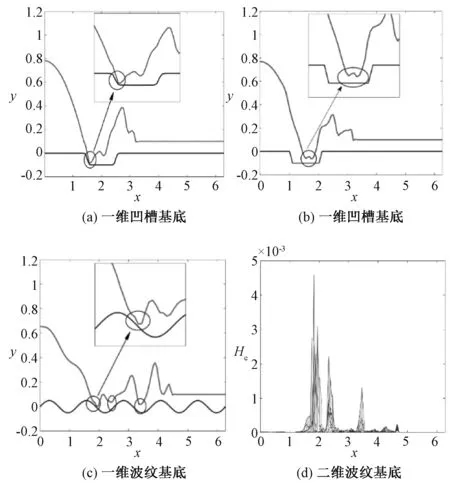
图6 液膜厚度和扰动能量图

2.3 粗糙度的影响

因扰动能量分布不均匀,为确定不同基底上的总扰动能量,利用式(17)对扰动能量在整个周期内积分,可得整个基底的扰动能量,如图7(a)和7(b)所示,图7(c)为非平整基底的Eu与平整基底Ep的比值λ。

(17)

由图7(a)和7(b)可知,在0平整基底>二维波纹基底>一维波纹基底>二维凹槽基底,如图7(c)所示。当A从0.1增大到0.5时,λ2w、λ1w均出现显著下降,这说明随粗糙度增加,两种波纹基底对扰动的抑制作用不断加强,由此可知波纹基底对粗糙度的敏感性更强,而凹槽基底对粗糙度的敏感性更弱。另外,指进现象中手指长度随粗糙度增加而伸长,表明手指长度与粗糙度呈正相关,如图7(d)所示。

2.4 凹槽与波纹基底

微机电领域更关注凹槽与波纹基底形貌对薄膜的影响[24,25],其原因是受加工工艺影响,没有绝对平整的基底,而非平整基底中凹槽与波纹基底最为常见,研究其对指进现象的影响具有实际意义,因此本节分析凹槽与波纹基底形貌对指进现象的影响。

图7表明,粗糙度相同时,一维凹槽基底的扰动能量最强,而二维凹槽基底的扰动能量最弱。其原因是在超薄液膜区,一维凹槽基底比二维凹槽基底的液膜厚更薄,对扰动的抑制作用更弱,因此扰动能量更强,如图6(a)和6(b)所示。图5(a)表明:一维凹槽基底扰动能量的分布呈两侧大中间小的特征,结合图8(a)可知,扰动能量小的位置不仅指进现象较弱,且手指长度和宽度都较小,而在扰动能量较大处,手指演化特征更加明显,该结论与Warner等[29]结果相吻合。

图7表明,在同一时刻下两种波纹基底下的扰动能量均小于平整基底,由此可知波纹基底对扰动能量的增长有抑制作用。但一维和二维波纹基底情形下的扰动能量差别较小,即波纹基底的空间维数对扰动能量的影响较小。由图9可知,一维波纹基底超薄液膜区处的手指演化特征更均匀,指长明显小于二维波纹基底情形。二维波纹基底Ⅰ处的液膜厚度梯度更大,手指的补充液更多,指长更长;而Ⅱ处液膜厚度梯度较小,手指补充液较少,因此指长更短,手指演化并不充分,这与Warner等[29]模拟结果一致。

图9 基底液膜厚度

3 分裂与屏蔽效应

3.1 分裂效应

Hamaroui等[12]的实验研究发现,活性剂浓度与预置液膜厚度将影响指进现象中的指尖分裂程度,如图10所示。Edmonstone等[32]的模拟研究指出,指进现象中会衍生出手指的分裂和屏蔽效应,但其未考虑基底对手指分裂等特征的影响。

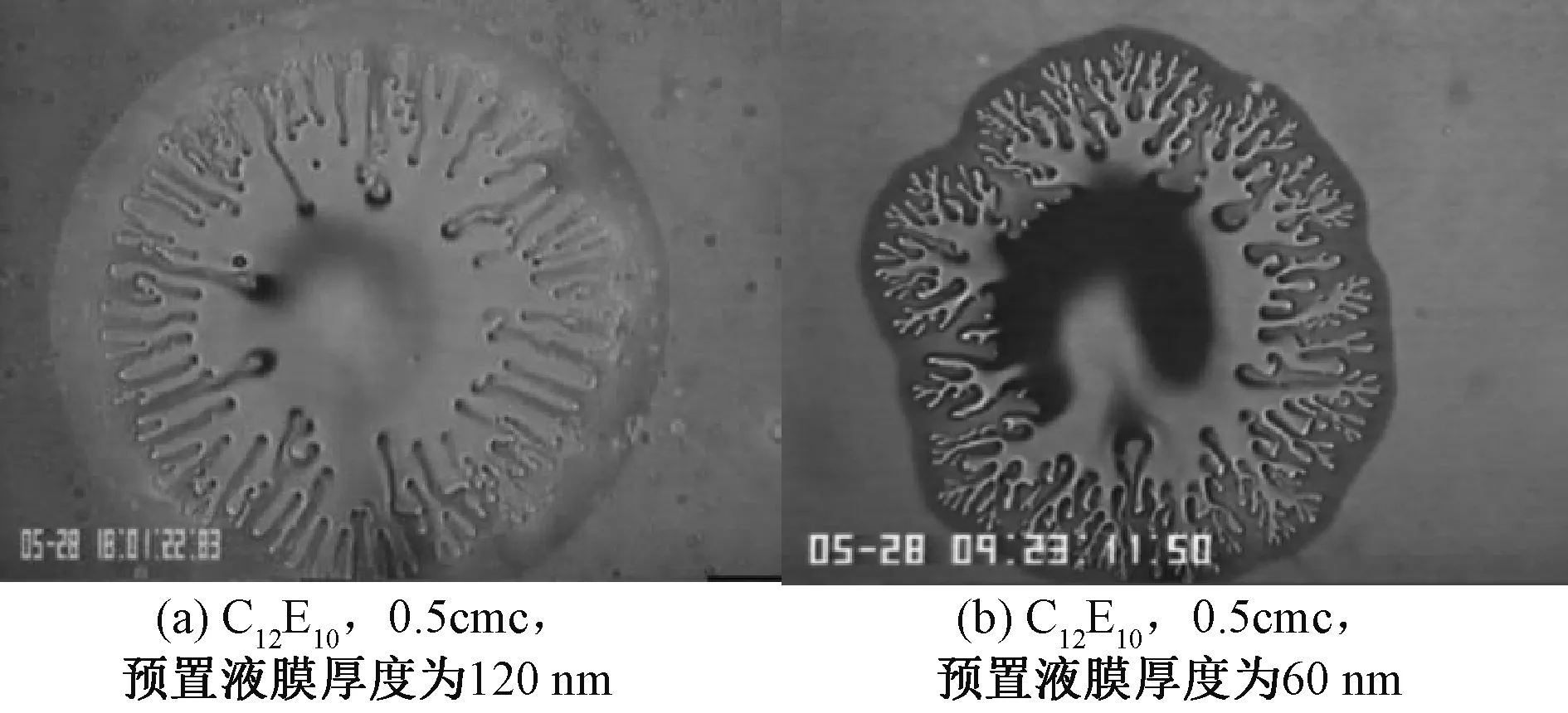
图10 含活性剂液滴铺展

为此,下文分析基底形貌和粗糙度对指进现象中分裂效应的影响。如图11所示,在t=30时由局部放大图可知,此时手指并未发生分裂,随时间持续,t=70时手指前端变宽,出现可衍生出新手指的先兆特征,在t=90时在该位置处手指发生分裂,上述模拟结果与实验现象[12]总体一致。

图11 二维凹槽基底的尖端分裂

为进一步揭示基底形貌和粗糙度对手指分裂效应的影响,采用分形分析指进现象的几何特征。分形维数是定量描述对象分形特性的重要参数,对于满足严格自相似规律的图形来说,利用自相似维数来进行分析准确高效,而本文研究的指进现象并不满足严格自相似,为此采用盒计数维数来开展[33],其表达式为式(18):

(18)

式中:k为正数,logk是常数项,r→0,logr→∞,可以忽略。

为验证计算结果的正确性,用相同的办法计算谢尔宾斯基地毯模型,计算结果为1.896 2,其分形维数的理论数值为log(8)/log(3) ≈ 1.893[34],计算误差小于1%。

分形维数计算域为超薄液膜区,结果如图12所示。随时间持续,手指不断演化,手指的分形维数不断增大。对比图12(a)和12(b)可知,手指分形维数随粗糙度增加而增大,即增加基底粗糙度是导致分形维数增大的重要因素。当A从0.1增至0.5时,不同形貌基底间的手指分形维数差值均减小,其中d2w与d1w的差值从0.14减少到0.06,由此可知:当粗糙度增大,基底形貌对手指分裂的影响降低,不同形貌基底间的手指分形维数差别减小。由图12可知,d2w>d1w,d2c>d1c,其原因是不考虑重力影响时,增加基底沿y方向的变化后,将出现沿y方向的横流,从而加速手指的分裂。

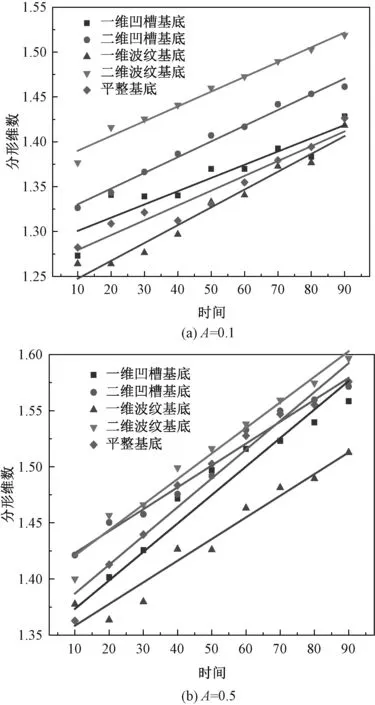
图12 不同粗糙度下手指分裂的分形维数

3.2 屏蔽效应

已有实验和模拟[12,32]表明,指进现象演化过程中,不仅有手指的分裂效应,还有屏蔽现象,如图13(a)和13(b)所示。屏蔽效应的出现会进一步增强手指演化的不均匀性,为观察不同形貌基底中屏蔽效应的强弱,下文给出不同粗糙度下的手指方差,如图13(c)所示。

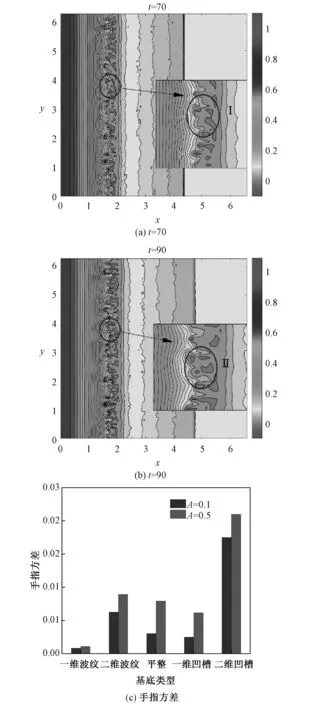
图13 手指屏蔽效应与手指方差

手指屏蔽效应的演化过程如图13(a)和13(b)所示,t=70时,图13(a)Ⅰ处有两根较长手指,其中间手指较短。在70

从图13(c)可知,手指方差随A增加而增大。二维凹槽的手指长度方差最大,由图4(a3)可知,凹槽两侧形成4根较长手指,但凹槽内的手指不明显。其原因为:忽略重力影响时,凹槽内手指的补充液绕过二维凹槽,提供给凹槽两侧手指,从而导致两侧指的伸长速度较大,槽内手指的演化不明显。

4 结 论

基底形貌对基底扰动能量的强弱与分布影响较大,非平整基底中:一维凹槽基底会强化扰动能量,其他基底则抑制扰动能量,基底形貌通过影响超薄液膜区的液膜厚度来改变基底扰动能量。与凹槽基底相比,波纹基底对粗糙度的敏感性更强,其扰动能量随粗糙度的变化更剧烈。基底扰动能量与粗糙度呈正相关,当A从0.1增至0.5时,基底的扰动能量也随之提高一个数量级;

基底粗糙度与基底形貌均影响手指分形维数。当A从0.1增至0.5时,不同基底手指分形维数均增大,手指分裂效应增强,但基底形貌对手指分裂的影响降低,且不同形貌基底间的手指分形维数差别减小。增加基底沿y方向的变化将加速手指的分裂。

屏蔽效应增强手指的不均匀性,增大手指间的方差,增加基底粗糙度将强化指进现象中手指的屏蔽效应。出现屏蔽现象的根本原因是:长手指的生长汲取了短手指的补充液,阻碍短手指的伸长,从而出现屏蔽现象。