新型双出杆活塞式磁流变减摆器结构设计及性能研究
2023-10-16田静张亚男
田静,张亚男
(中国民航大学 航空工程学院,天津 300300)
飞机起落架减摆系统是为飞行员和乘客提供最佳的整体乘坐体验。传统的被动油液式减摆系统直接对起落架受到的激励作出反应,不论跑道和负载情况如何,阻尼力不能实时调节。相比之下,磁流变(Magnetorhe-ological,MR)减摆器通过电流控制磁场强度,进而改变磁流变液(Magnetorheological fluid,MRF)黏度输出实时变化的阻尼力,以改善飞机动态稳定性和提高乘客舒适度[1-2]。
磁流变阻尼器(Magnetorheological damper,MRD)因出力连续可调、响应速度快及能耗低而得到广泛应用。为保证MRD 发挥最优性能,学者们优化设计了多种结构形式。线圈增加能产生较大的阻尼力,但多级活塞或多级线圈导致行程受限[3-5]。线圈外置式有更好的散热性能,与使用外部线圈相比,线圈内置可实现更高压力容量,更快控制响应和更少泄露[6]。单筒MRD 是目前最常见的MR 装置,结构简单且内部元件少,但在工作时一直处于高压状态,限制了应用。与单筒MRD 相比,标准的双筒MRD 采用同心缸筒,内筒中装有活塞,目前对其的研究及应用工作尚未完成[7]。
MR 减摆器是抑制摆振最关键的出力部件,影响其减摆性能的重要因素是结构尺寸与磁路设计。本文针对传统结构存在的问题,提出了一种新型结构的MR 减摆器,以改善减摆性能。此减摆器采用内置双线圈、双筒式结构,线圈固定,阻尼通道有效区域紧邻线圈,内、外对称双阻尼通道充分有效利用磁场。同时为了获得 MR 减摆器的力学特性,文中对减摆器进行了磁场仿真,以验证设计的合理性。
1 飞机减摆需求分析
飞机前轮摆振是一种有害的自激振动,严重时会导致整个起落架失效,进而机毁人亡。当扭力臂无法完全抑制飞机滑跑速度达到一定值时产生的快速摆动情况,就需要减摆器通过液压阻尼的作用来消除摆动。由于外界干扰引起的起落架系统摆振在3 个周期内衰减到初始扰动幅度的1/4 以下或消失,则称系统稳定[8]。
参照某型无人机,结合MRD 的特点,确定飞机前轮MR 减摆器的设计要求。减摆器安装在支柱水平方向,两端铰接固定,参数取值为:总长度约为170 mm、缸筒直径不超过50 mm、振幅为0.7~9 mm、频率为3~15 Hz、行程为 ±10 mm[9]。
当飞机前轮发生0.5°摆振时,传递到MR 减摆器活塞杆的直线位移约为0.7 mm,以此为基数整数倍设计工况。不同工况下,减摆器所需要输出的最小阻尼力如表1 所示[10]。

表1 不同工况下的理论阻尼力Tab.1 Theoretical damping force under different operating conditions
2 减摆器结构优化设计
2.1 减摆器结构对比分析
图1a)为单线圈内置式MR 减摆器[9],线圈在腔体内部使磁场得到充分利用,但随着活塞往复运动,导线在活塞杆中心线槽内反复承受摩擦磨损,可靠性降低。图1b)为单线圈外置式MR 减摆器[11],缸筒外置线圈有利于散热,降低了对MRF 的热效应,但是线圈外置导致所占空间增大。图1c)为双线圈内置式MR 减摆器[10],线圈缠绕在端盖上固定不动,避免了导线随活塞杆往复运动的缺点,具备较高的可靠性,但退磁区域较短,不能充分退磁,且阻尼通道有效区域距离线圈较远,容易造成磁力线减弱,在摆振实验中输出阻尼力较低,达不到的3 个周期内将摆振振幅削减到原振幅 1/4 的要求,并不能有效抑制摆振。
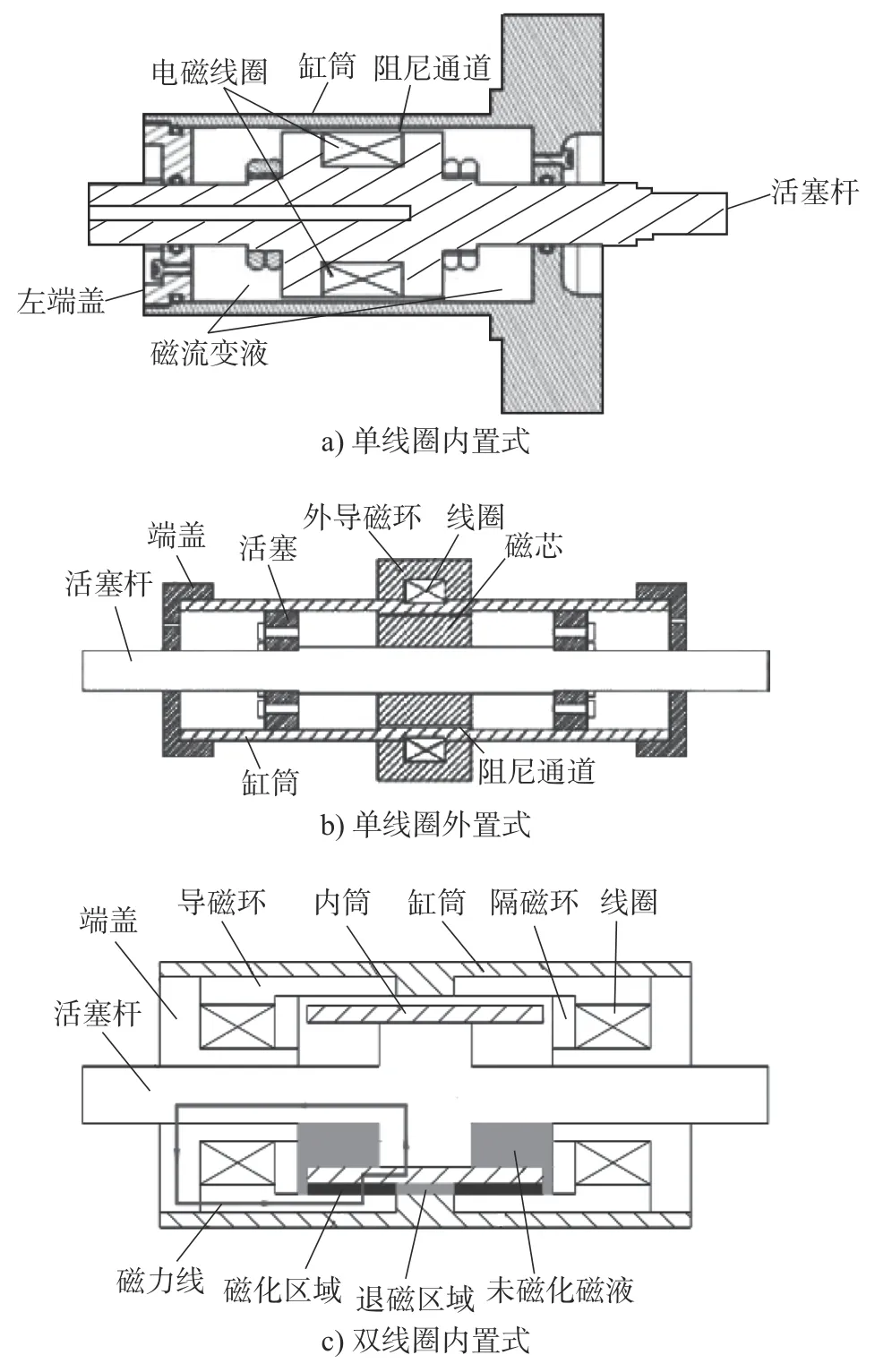
图1 不同结构形式MR 减摆器Fig.1 Different structural forms of MR dampers
2.2 减摆器结构设计
针对上述MR 减摆器的不足之处,本文提出了一种新型结构形式的双出杆活塞式MR 减摆器,如图2 所示,采用压差式结构。减摆器两端内置固定双线圈,引线安全性高,且靠近端盖便于散热;活塞在中间往复运动,具有充足行程。阻尼力通过活塞往复运动迫使MRF 流过阀式结构固定极板间隙产生,通过调整内筒厚度可以改变阻尼通道间隙。环形间隙和通道中的磁场使MRF 产生屈服应力,阻尼力的大小随屈服应力发生变化,因此MR 减摆器的设计需要进行详细的磁场分析,最大限度的提高环形间隙中的磁场强度,避免饱和现象出现。

图2 新型双出杆活塞式MR 减摆器原理图Fig.2 Schematic diagram of a novel double-out-rod piston MR damper
减摆器由导磁环、隔磁环、垫片、活塞、端盖、内筒、外筒和线圈构成。端盖和导磁环优先考虑磁学性能较好的DT4 电工纯铁。缸筒作为受力构件,隔磁环和垫片也承受一定程度的挤压力,可选用导磁率近似于空气的不锈钢。活塞杆作为磁路的一部分,又要承受拉力,选用剩磁影响较小、材料强度高的45#钢。内筒两端与导磁环和端盖形成有效阻尼通道,选用DT4 电工纯铁;内筒中间位置与外筒形成退磁区域,选用不锈钢。
为防止MRF 泄露,需进行密封设计。密封区域如图3 所示,因活塞杆往复运动,区域1~3 采取动密封,使用具有自润滑效果的斯特封,同时兼顾润滑与密封要求;其余位置为静密封,采用O 型圈,且边缘处加涂密封胶[12]。
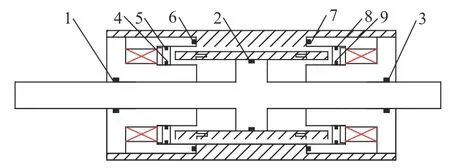
图3 密封部位Fig.3 Sealing components
MR 减摆器主要结构尺寸如图4 所示,设活塞杆的半径为R0,线圈环槽磁芯半径R1,导磁环内半径为R2,外筒内半径为R3,外筒外半径为R4,活塞直径为R5,线圈横截面积的长度和宽度分别为Lc和Wc,磁流变液有效阻尼通道的长度和间隙分别为Lm和tm,退磁区域的长度和宽度分别为Ln和tn,端盖厚度为Lg。
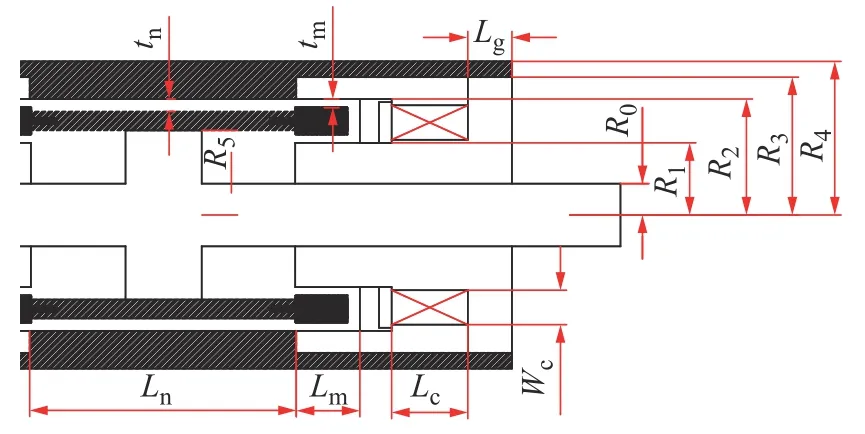
图4 MR 减摆器结构尺寸Fig.4 MR damper structural dimensions
2.3 关键尺寸设计
根据设计需求,确定外筒长度为110 mm,直径为49 mm,活塞行程为±15 mm。环形阻尼通道间隙太小容易发生堵塞,而间隙过大则输出阻尼力太小,一般取0.5~ 1.5 mm,参照之前减摆器优化设计结果,将阻尼间隙取0.8 mm,退磁区域间隙取1 mm。
活塞杆直径需满足
式中:F为减摆器最大输出阻尼力,F=2 kN;[σ]为45#钢抗拉强度,[σ]=600 MPa;n为安全系数,n=2;兼顾MR 减摆器采用与原有减摆器相同的方式安装到起落架上,活塞杆半径取5 mm。
设S1、S2、S3分别为活塞杆、磁芯和导磁环的横截面积,AMR是MRF 通道有效横截面积,电工纯铁、45#钢和MRF 的饱和磁感应强度分别为BsatDT4=2.1 T,Bsat45=1.75 T,BMR=0.7 T,则活塞杆、磁芯和导磁环的横截面积必须满足:
由此可确定磁芯和导磁环的最小极限面积S2min,S3min。MR 减摆器一些关键尺寸的取值范围可通过最小极限面积来确定,即:
综上所述,MR 减摆器尺寸参数如表2 所示。
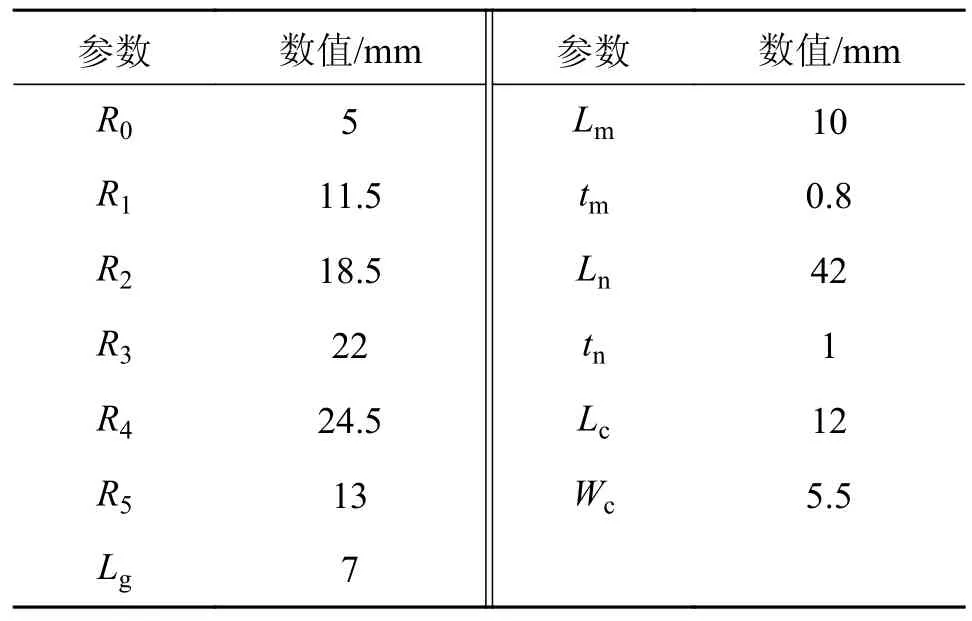
表2 结构尺寸参数Tab.2 Structural dimension parameter
通过CATIA V5R21 进行MR 减摆器三维建模及零件装配,如图5 所示。
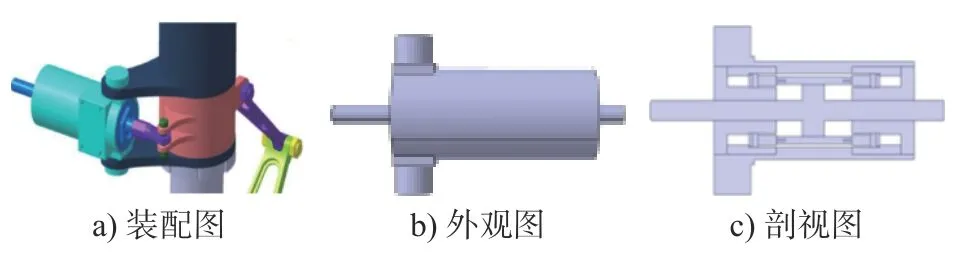
图5 MR 减摆器装配图Fig.5 MR damper assembly diagram
3 磁路设计
所设计的MR 减摆器,既要保证阻尼通道有效区域内MRF 达到饱和,又要防止发生磁芯饱和现象,更需要防止磁路的一个区域不会过早饱和而造成瓶颈效应。磁路的精确建模求解是非常困难和复杂的,计算通常采用近似求解。
3.1 磁路分析
根据基尔霍夫磁定律(式(6))、安培环路定律(式(7))和电路的磁通守恒定律(式(8))来分析磁路。
式中:Hk和lk为第k条磁路的磁场强度和有效长度;Nc为线圈匝数;I为电流值;H为磁场强度;l为磁路有效长度;φ为磁通量;Bk和Ak为第k条磁路的磁感应强度和磁通面积,Bk=μ0μkHk,μ0为真空磁导率,μ0=4π×10-7Tm/A,μk为第k条磁路材料的相对磁导率。磁路走势如图6 所示。
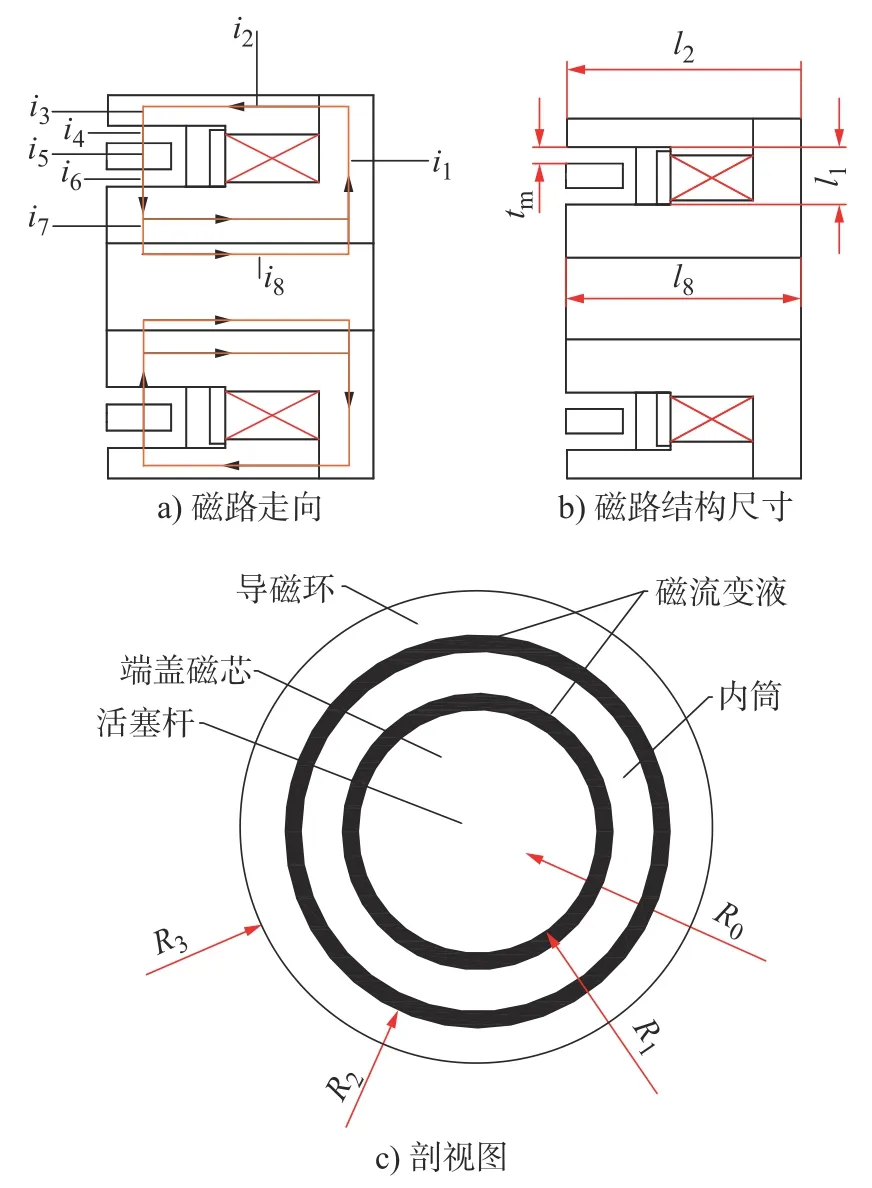
图6 磁路走势Fig.6 Distribution of magnetic flux
根据图6 和式(6)~式(8)可得:
展开式(9)和式(10)得:
式中:HMR和BMR分别为MRF 阻尼通道处的磁场强度和磁感应强度;lMR为MRF 通道有效长度,lMR=2tMR。
联立式(11)和式(12)得
为了简化计算,假设每种材料的相对磁导率为常数[3],即MRF 相对磁导率μMR=2.5、DT4 相对磁导率μDT4=1 600、45#钢相对磁导率μ45=1 000。
线圈左右两侧翼磁阻面积按照柱体体积与其半径比值来计算[12],由于活塞杆与端盖磁芯材料不同,因此在中心处为并联磁路。各段磁导率及横截面积计算方法为:
通过计算可得NcI=419.95 A。额定工作电流为1.25 A,此时激励线圈需要缠绕的匝数为335.96 匝,只要缠绕圈数大于335.96 匝就能满足磁路要求,因此缠绕线圈 350 匝。线圈环槽横截面积为66 mm2,将直径为0.25 mm 的漆包铜线紧密排布在铁芯上,考虑手工绕线存在误差,设置缠绕率为0.6,理论上可缠线806 匝,因此线槽空间充足。
3.2 磁场仿真
为了获得阻尼通道处磁感应强度随电流的变化情况,基于有限元软件ANSYS/Emag 2020 R1 对MR 减摆器进行电磁场仿真,该软件具备很强的鲁棒性。减摆器为圆柱形对称结构,因此只需要建立二维模型(图7)便可以很好的观察出磁场特性。
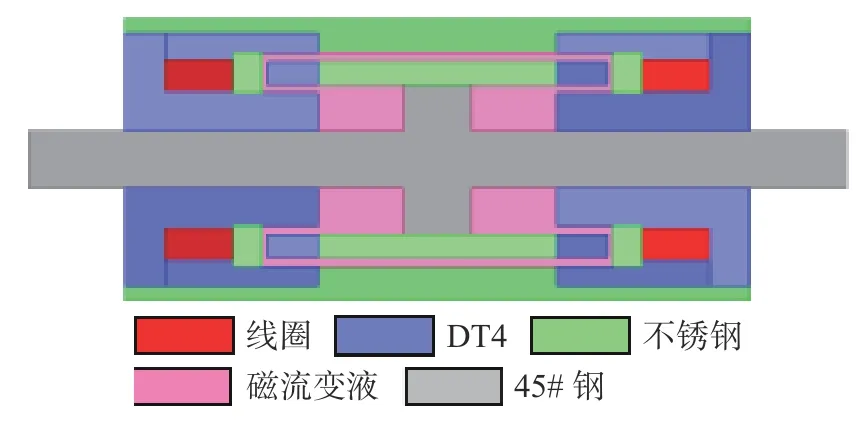
图7 MR 减摆器建模示意图Fig.7 Schematic diagram of the MR damper model
建立模型后,将 DT4 电工纯铁(图8a)),45#钢(图8b))[13]以及MRF-132 DG(图8c)和图8d))的导磁性能曲线自定义添加到材料库中。
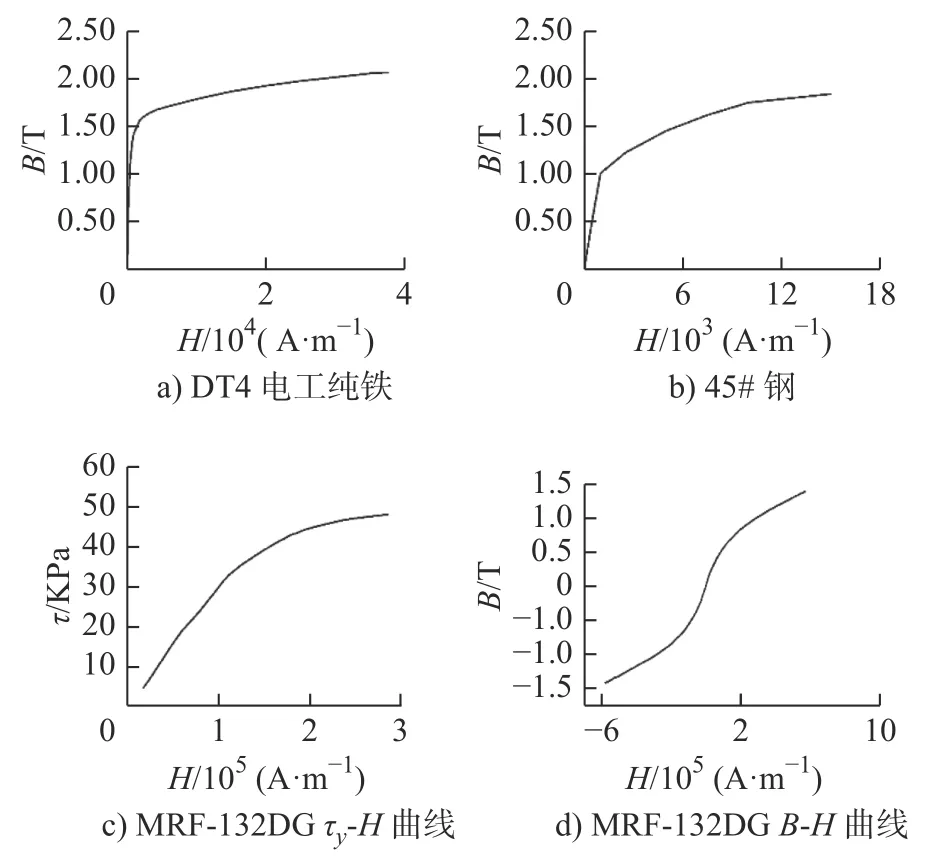
图8 材料导磁性能曲线Fig.8 Magnetic permeability performance of the materials
分别施加不同强度的I(电流)进行电磁仿真,结果如图9 所示,随着电流增大,减摆器内部的磁感应强度B逐渐增大;深颜色处B较高,内、外阻尼通道有效区域内颜色较为均匀,说明B沿阻尼通道分布较为均匀,在隔磁环外侧B最大,这是因为此处磁通面积较小的缘故。最大电流I=1.25 A 状态下磁路最大磁感应强度为2.069 4 T,与DT4 材料的饱和磁感应强度一致。阻尼通道有效长度外B均低于0.05 T,未出现严重漏磁现象。
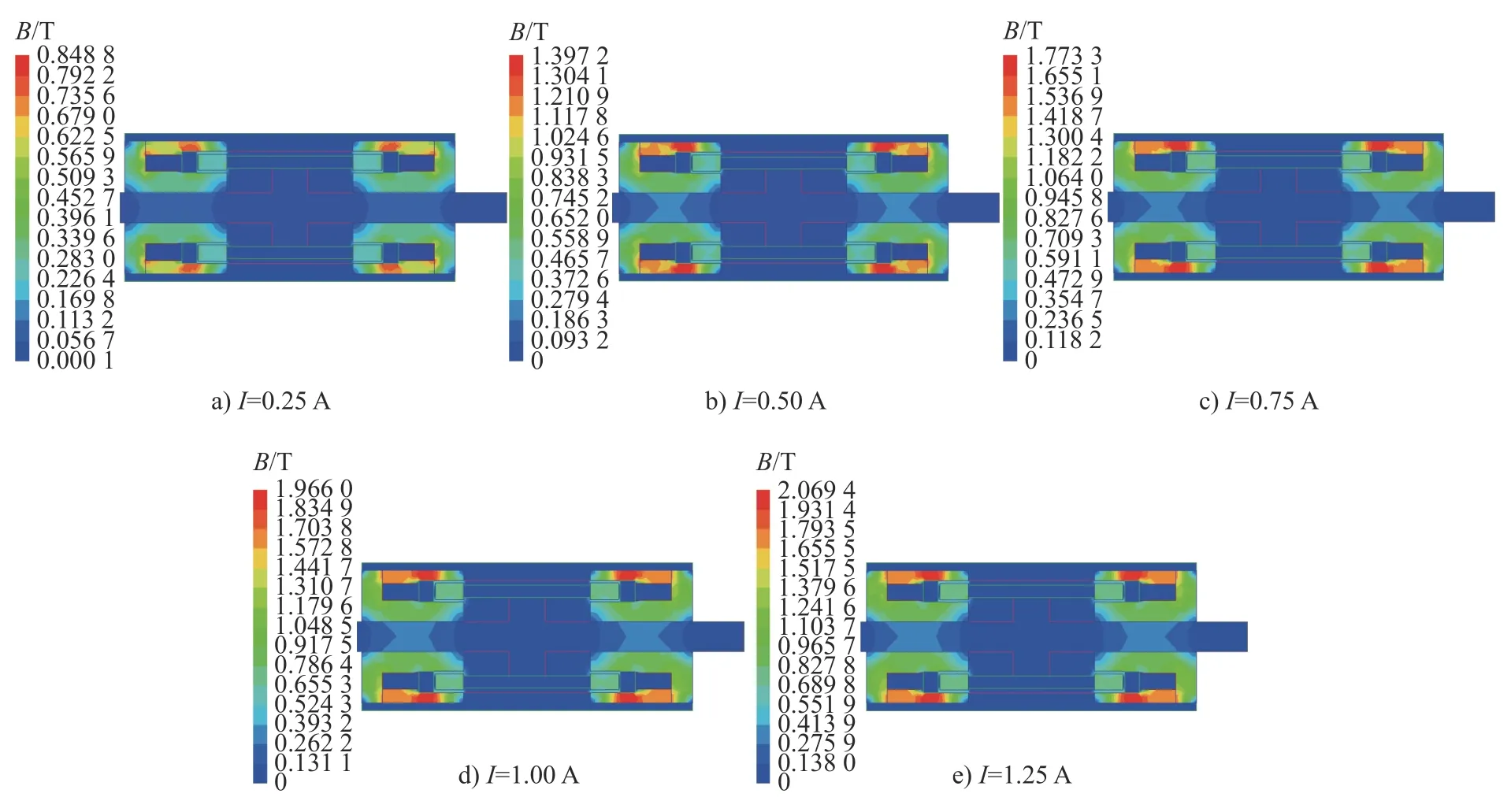
图9 磁感应强度云图Fig.9 Cloud map of induction intensity
查看磁力线分布,通过图10 观察到磁力线沿通道全长等距排列,确保间隙内磁场分布一致,且垂直穿过有效阻尼通道,几乎没有出现漏磁现象,较好地实现通道有效。
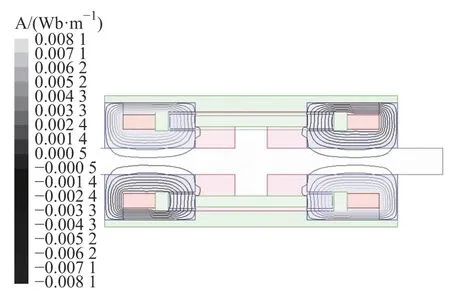
图10 磁力线走势图Fig.10 Distribution of magnetic field lines
为了精准的量化分析阻尼通道内磁感应强度的变化趋势,分别在内、外阻尼通道有效区域中心层绘制一条直线,查看B变化趋势。图11 为不通电流下内、外阻尼通道有效长度内的B,沿轴向方向,除内筒端面以及退磁区域边缘处B变化较大外,磁化区域曲线波动较小,因此可按匀强磁场处理。由于材料的导磁性能具有非线性特征,在小电流时内、外阻尼通道的磁感应强度随电流变化较大,随着外加电流的增大MRF 逐渐趋于饱和,导致B变化幅度减小,且磁力线通过导磁环进入外阻尼通道,在隔磁环外侧磁通面积突然减小,因此外阻尼通道处磁感应强度的变化幅度略大于内阻尼通道。
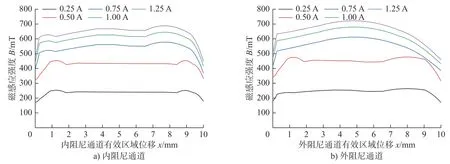
图11 阻尼通道有效长度磁感应强度BFig.11 Magnetic induction intensity along the effective length of the damping channel
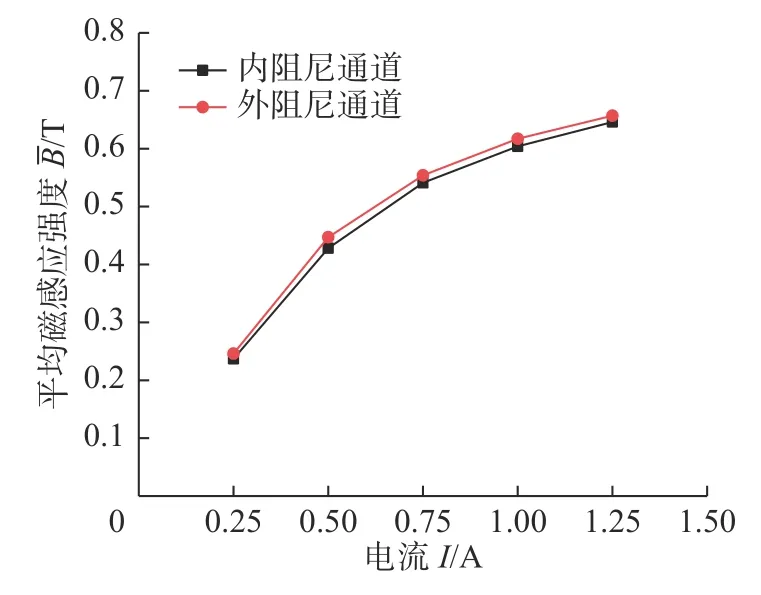
图12 阻尼通道平均磁感应强度Fig.12 Average magnetic induction intensity in the damping channel
4 力学特性分析
4.1 力学性能数学建模
MR 减摆器由活塞分为左、右两腔,完全充满MRF。摆振发生时,带动活塞往复运动,迫使MRF从活塞一侧的腔室通过两端的阻尼通道和内外筒之间的环形间隙流到另一侧腔室,减摆器运动示意图如图13 所示。

图13 MR 减摆器运动示意图Fig.13 Schematic diagram of the motion of the MR damper
假设减摆器为准静态特性,MR 减摆器的阻尼力可表示为
联立式(15)~式(17)得MR 减摆器输出阻尼力为
从式(18)可以看出,MR 减摆器的输出阻尼力由黏滞阻尼力、库伦阻尼力和机械摩擦力这3 部分组成,其中库仑力是可调阻尼力。阻尼力与阻尼通道间隙成负相关,与阻尼通道长度、MRF 黏度及活塞有效面积成正相关。
动力可调系数(定义为最大电流下库仑力与黏滞力之比[15])也是评价MR 减摆器整体性能的重要参数,较大的动力可调系数可提供较宽的MR 减摆器控制范围。考虑机械摩擦力,动力可调系数表示为
对于小型MR 减摆器,可近似认为Ff=Fη[12]。
设MR 减摆器活塞的振动行程为 2Amax,振动频率为f,则在t时刻活塞的相对位移x为
活塞与缸筒内壁的相对速度v为
假设MR 减摆器的阻尼特性是线性的,设阻尼系数为K,那么阻尼力与速度成正比,即
联立式(20)~式(22)得减摆器示功曲线是一个椭圆,即
4.2 力学性能分析
选用美国 Lord 公司的 MRF-132DG 号磁流变液,屈服强度τy与磁感应强度B的关系为
通过式(24),结合图11 可以计算出不同电流下MRF 屈服强度。将表3 得到的MRF 屈服强度值带入式(17),计算得到在不同速度、不同电流下系数c的取值,如表4 所示。
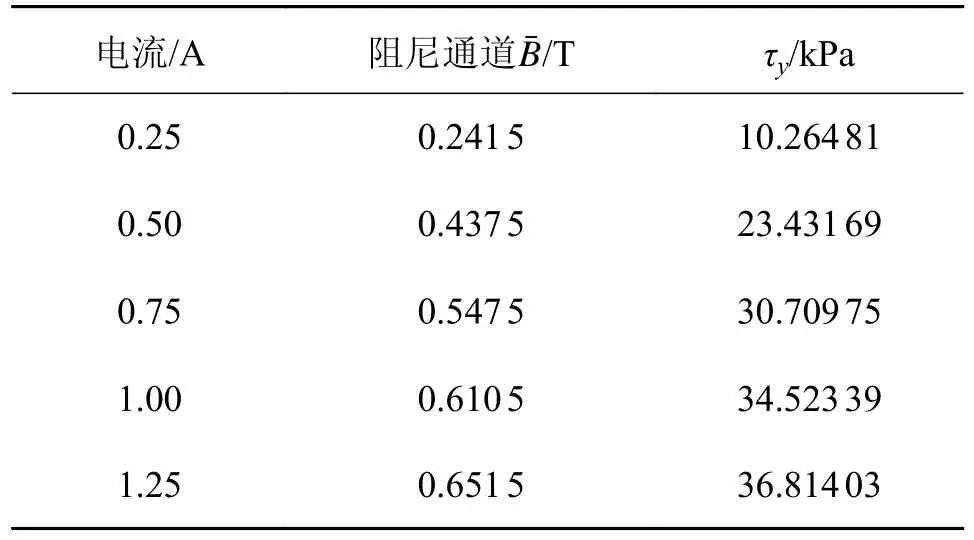
表3 不同电流下MRF 屈服强度Tab.3 MRF yield strength under different currents
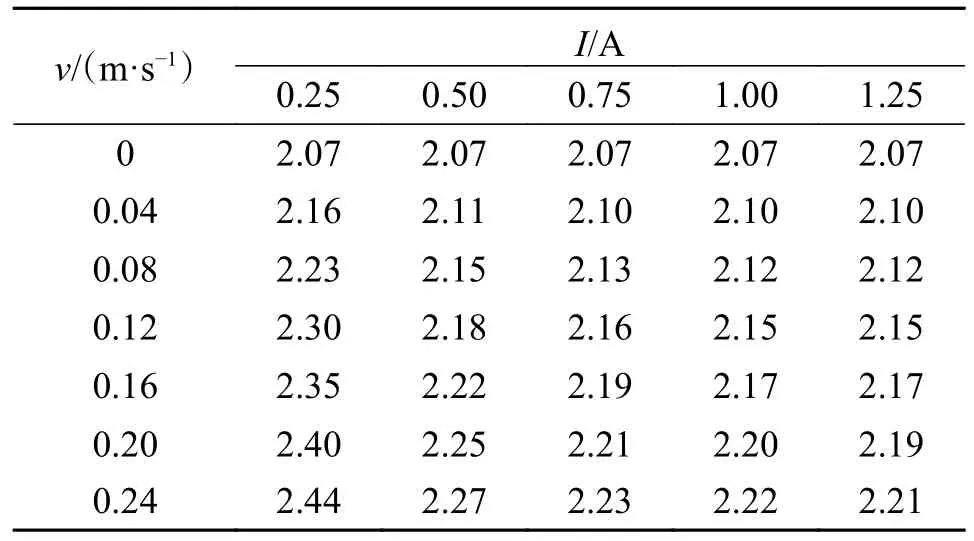
表4 系数c 数值Tab.4 Numerical values of the coefficient c
如图14 所示,联立式(18)、表3 及表4 得到MR 减摆器输出阻尼力随速度变化曲线,随着电流增加,输出阻尼力增加,且阻尼力增速变缓,这是因为随着电流增加,线圈产生的磁场强度增强,MRF逐渐达到饱和磁感应强度。在1.25 A 电流下,速度为0.04 m/s 时,输出阻尼力为1 772.18 N;速度为0.24 m/s 时,输出阻尼力达到1 999.02 N;最大输出阻尼力满足减摆需求。
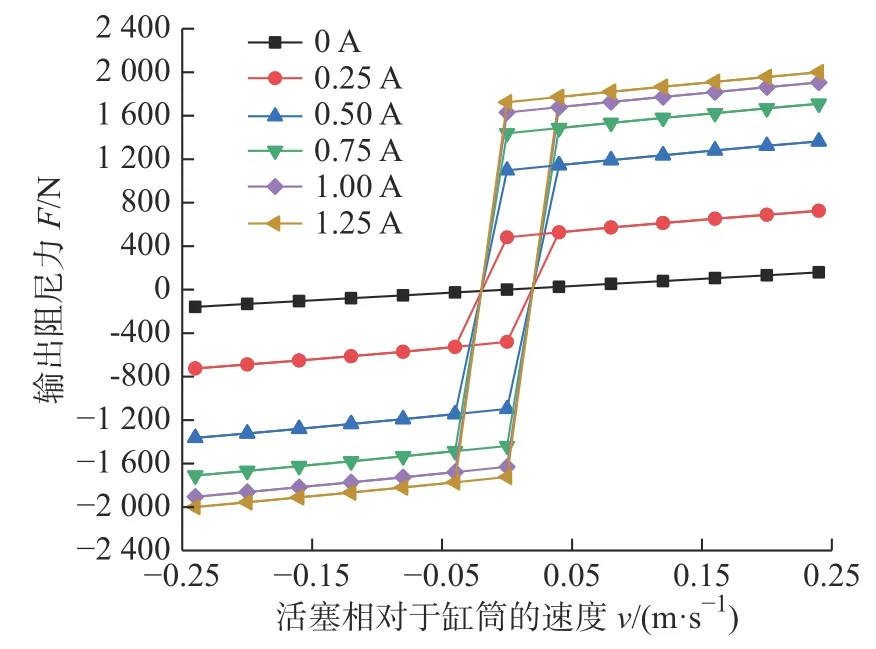
图14 MR 减摆器F-v 曲线Fig.14 The F-v curve of the MR damper
根据式(18)和式(19)计算得到MR 减摆器输出阻尼力动力可调系数,如图15 所示,在1.25 A 最大供电电流下,分析不同速度下阻尼力动力可调系数的变化趋势,在任何工况下,动力可调系数均大于12,可调性高,输出阻尼力控制范围较大;随着速度增加,可调系数变小,且减小速度变缓。
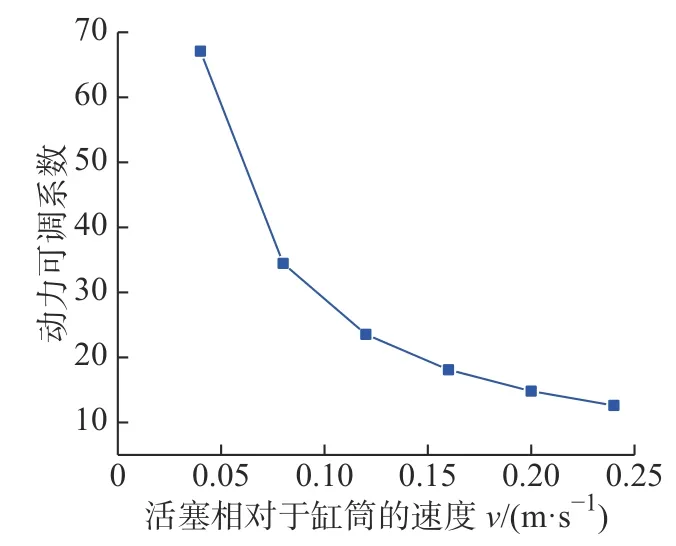
图15 不同速度下的动力可调系数Fig.15 The dynamic adjustable coefficient at different speeds
在频率5 Hz,±10 mm 行程内,减摆器示功曲线如图16 所示,示功曲线近似于椭圆,随着电流值的增加,阻尼力增加,但增速变缓。
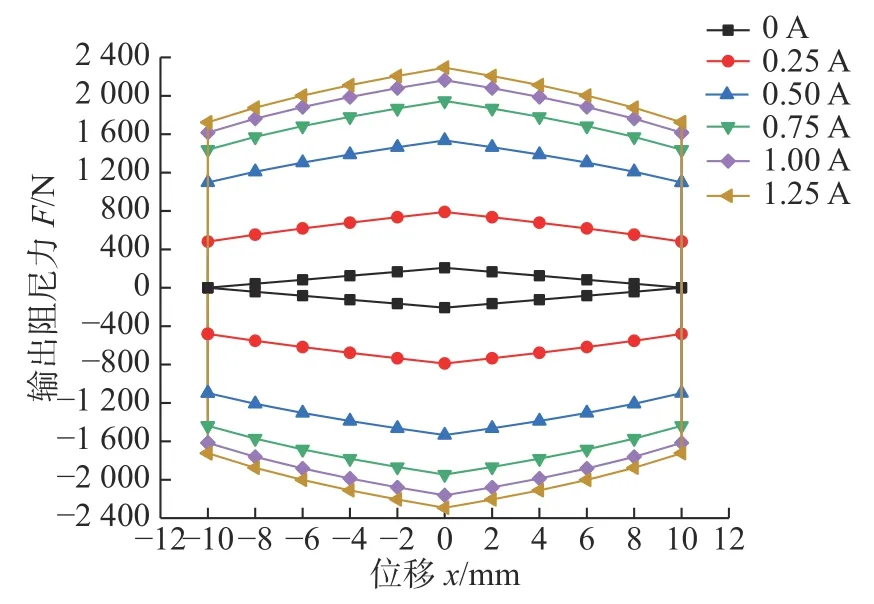
图16 MR 减摆器示功图Fig.16 Indicator diagram for the MR damper
5 结论
1)提出的新型压差式结构双出杆活塞式MR 减摆器,内置固定双线圈,内筒与外筒及端盖形成的环形内、外对称双阻尼通道充分有效利用磁场,磁场有限元仿真表明,设计的磁路结构切实可行,弥补了传统结构MR 减摆器的不足。
2)在0~1.25 A 的供电电流下,输出阻尼力随着电流增加逐渐增大,最大电流下,输出阻尼力近2 kN;在任何工况下,动力可调系数均大于12,可提供较宽的控制范围;示功曲线近似于椭圆;MR 减摆器力学性能满足减摆需求。
3)后续将进行MR 减摆器的结构优化设计及阻尼特性试验,以及飞机前起落架减摆系统性能研究。
