轮轨综合磨耗下对高速列车动力学性能的影响

杨洋，吴涛，林凤涛，黄琴，庞华飞，邹亮

（华东交通大学 载运工具与装备教育部重点实验室，南昌 330013）

高速铁路的出现和发展，使人们能够享受快速且舒适的交通出行方式，带来了许多便利。Peng 等[1]提出了车轮多边形的一些演化规则，建立了车轮多边形磨损演化的一般条件。但由于速度的提高，列车轮轨关系会更加严峻，其产生的振动会更为剧烈，对此会引起轮轨踏面磨耗损伤，较为常见的比如车轮表面上出现的多边形磨耗，以及轨道上出现的波形磨耗，对车辆整体运行的动态性能带来不利的影响，威胁行车的安全性。Mazilu 等[2]对轮对进行了弹性化的处理工作，并创建了轨道结构为有砟轨道的，且其与轮对之间接触作用的动力学模型，进行仿真计算后找出了在列车车轮踏面上出现3 阶次的车轮多边形磨耗的原由。Wu 等[3]通过现场试验和模型仿真，分析高阶车轮多边形产生高频冲击载荷的影响，从而产生高幅值和走形加速度。周殿买等[4]在对多边形磨耗发生的原由进行探究。李伟等[5]发现，列车在运营状态下，在轮轨踏面存在的磨耗激励，促使车轮发生一阶弯曲共振现象，使得在车轮表面上产生了9 阶多边形。陈伟[6]对高速列车上出现的多边形现象进行了深入的研究，发现高速列车车轮转动频率的大小，不能被列车轮轨系统引起的振动频率的大小整除时，从而导致了该现象的发生。杨晓璇等[7]对轮对的模态进行了计算，获取了轮对的自由模态，并对列车上的主要构件的振动性能做了测试试验。结果发现，车轮出现的扭转与其1 阶弯曲模态产生了模态共振现象，使得多边形现象发生在车轮表面上。李霞等[8]建立普通短轨枕轨道的三维实体有限元模型来找寻地铁运行区间形成125～160 mm 波长波磨的原因，通过仿真计算结果发现采用普通短轨枕使得轨道结构隔绝振动的能力较差，车辆在此轨道上运行通过时，钢轨与道床板之间，非常容易发生弯曲振动现象。肖乾等[9]通过分析车轮阶数和波深增加，认为纵向蠕滑率增大与脱轨现象有一定关系。吴越等[10]通过建立车轮多边形磨耗预测模型分析钢轨波磨并不是车轮多变形产生的根本原因。Gómez 等[11]对钢轨波磨的发展情况进行了预估，他们采用的办法是有限元与线性模型的组合形式，以此仿真模拟轮轨对应的不同固有频率下，钢轨波磨在各频率对应下的磨耗发展趋势。Correa 等[12]对影响钢轨波磨的相关因素展开了研究，采用了有限元方法，对不同车轮但处于同一转向架下进行了仿真计算，分析钢轨波磨与车轮存在的位移导纳和模态特性之间具有的相关性。Li 等[13]创建了轮轨的滚动瞬态接触的三维模型，仿真计算了由钢轨不平顺所引起来的车辆动态响应，结果发现，线路波磨会对轴箱加速度产生影响。赵新利等[14]研究轮轨在580 Hz 附件会引发轮轨共振，加剧轮轨表面磨耗。金学松等[15-16]总结了车轮非圆化幅值、波长、车速和轴重等因素对车辆动力学有显著影响，以及我国高速车轮多边形磨耗情况和特征，其显著特征是车轮多边形不均匀磨损。

上述研究中，对车轮多边形及钢轨波磨的形成机理及影响特性做了深入研究，推动了轮轨关系领域的进一步认识。对于车轮多边形及钢轨波磨的耦合状态对列车系统动力学行为的影响鲜有研究，本文针对车轮多边形与钢轨波磨问题，从轮轨力和振动加速度两个方面，系统地研究了这两种轮轨综合磨耗下对高速列车动力性能的影响。通过仿真的手段，创建高速列车刚柔耦合动力学模型；其次，将车轮多边形施加在车轮表面，钢轨波磨施加在钢轨表面上，对车辆的轮轨垂向力和垂向加速度进行分析，研究其响应规律。

1 轮轨综合磨耗数值模型

1.1 车轮多边形建模

对于车轮多边形的数学模型，假设车轮廓形不变，车轮半径差沿圆周方向呈周期性变化，用简谐函数法定义车轮周长的周期不平顺[17]，即：

式中：α0为初始相位角；α为车轮转过的角度；Δr为车轮圆周不圆顺的轮径差；A为不圆顺的幅值；r为不圆顺车轮的实际半径与圆周角有关。R为车轮滚动圆名义半径；n为车轮多边形化阶次，即在车轮滚动一周内车轮实际半径与车轮名义半径之差所形成的谐波周期数。

现场测试使用Mwheel 测试仪进行车轮粗糙度的测量，完整的获取了车轮多边形磨耗廓形，再对车轮进行镟修工作，在镟修完成后，再次对车轮踏面进行测量。Mwheel 测试仪及现场测量位置如图1 所示。

图1 Mwheel 测试仪及现场测量位置Fig.1 Mwheel test instrument and on-site measurement location

车轮磨耗踏面粗糙度水平定义为：

通过Mwheel 测试仪测量的镟前与镟后车轮多边形的数据如图2 所示。由图2 可知，车轮存在显著的以20 阶为主要阶次的多边形磨耗问题，并且在镟修后很好的去除了20 阶多边形。在后文的仿真计算中，本文也取多边形阶次为20 阶作为研究的主导阶次，研究其对列车引起的动态效应。

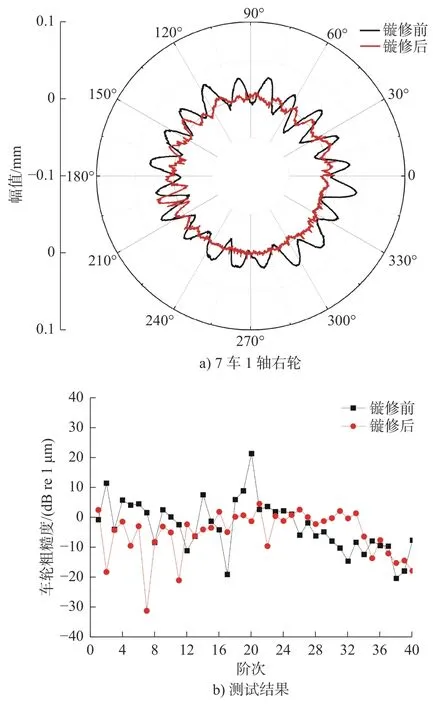
图2 实测20 阶车轮多边形测试结果Fig.2 Measured 20-order wheel polygon test results

车轮动态下由多边形车轮产生的轮轨激励频率f，其表达式为

式中：v0为车速；r为多边形车轮的实际半径；n为车轮多边形化阶次。

由方程式中也可以看出，当把车轮的半径看作为固定值而保持不变，列车运行速度以及车轮多边形阶数对多边形振动频率起关键作用，具体如表1所示。表中可以看出，频率的大小与v0和n呈正相关。当在某阶次下对应的车轮固有频率与其在运行振动频率十分贴近甚至相同时，将会出现共振现象，轮轨接触振动加剧。

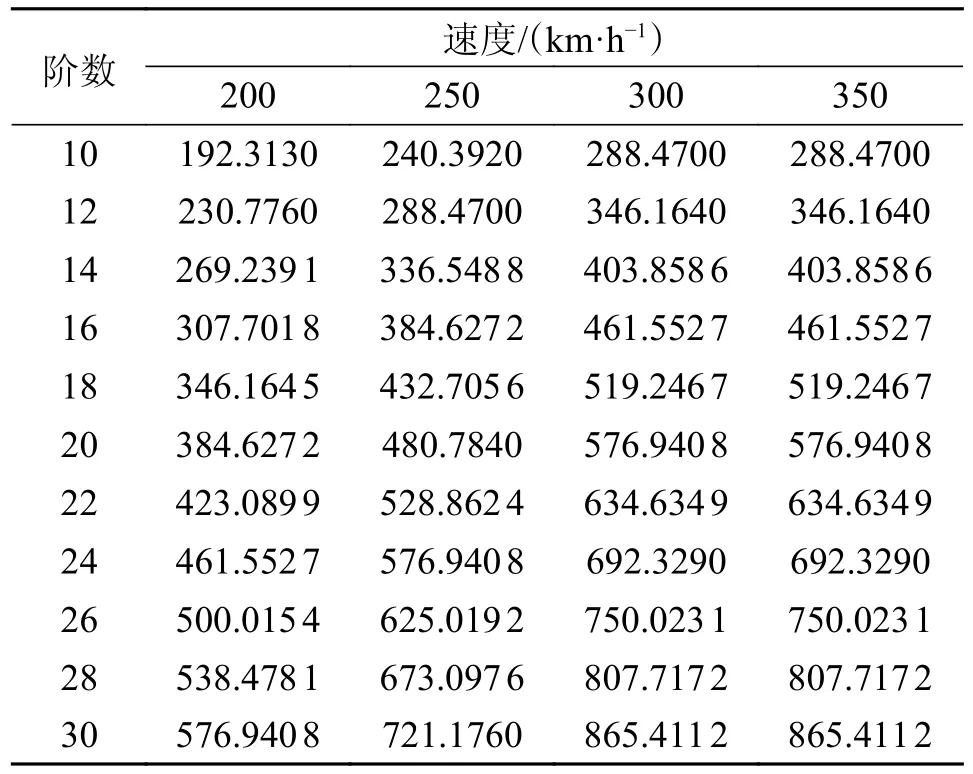
表1 不同阶次车轮多边形的特征频率Tab.1 Characteristic frequencies of different-order wheel polygons Hz

1.2 钢轨波磨模型

在分析钢轨波磨问题上，钢轨波磨简化为连续谐波激扰，本文采用国际铁路通用的余弦函数来描述其轨面的不平顺[18]。

方程式为

式中：L为波长；a为波深；N为波数。

通过控制钢轨波磨的波深和波长，可以得到在不同速度下它对轮轨间的动力学响应。在高速区段，波磨波长范围通常在130～160 mm，从安全角度考虑，选取120～160 mm 波长范围用于后续的动力学仿真。如图3 所示，为本文建立的120～160 mm 波长的钢轨波磨。

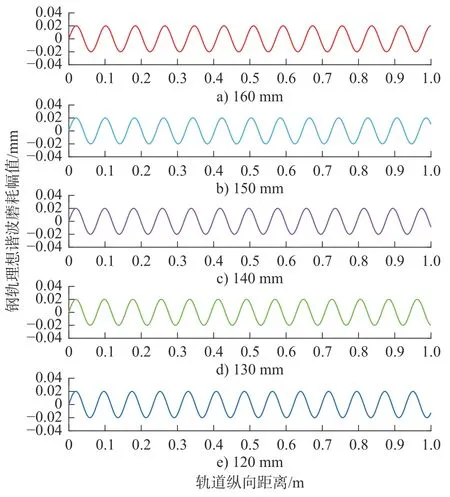
图3 钢轨表面不平顺Fig.3 Roughness on the rail surface

2 动力学模型建立

依照我国某型高速列车动车组动力学参数，基本参数如表2 所示，动力学模型包括包括车体、转向架、轮对的拖车模型。

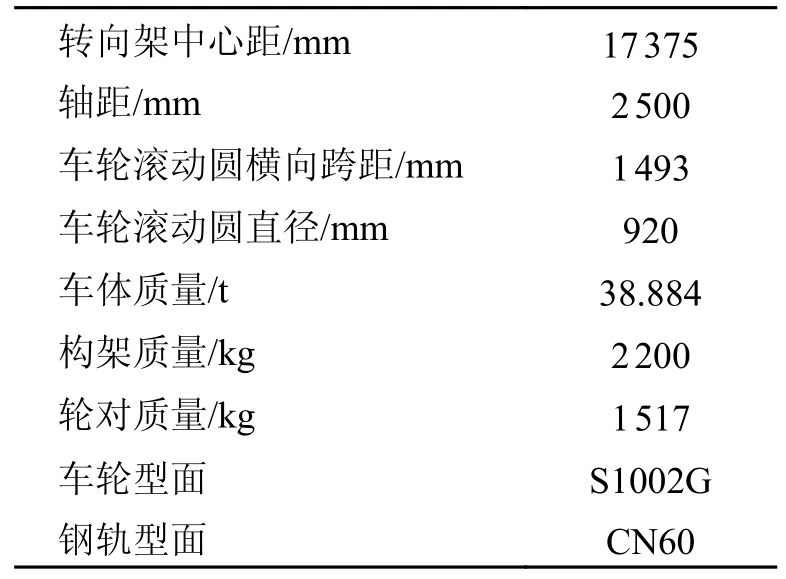
表2 车辆基本参数Tab.2 Basic vehicle parameters

轮对和构架之间通过一系悬挂和轴箱连接，构架和车体分别通过一系悬挂以及二系悬挂连接。该高速列车的拓扑关系图如图4 所示，车体、构架和轮对均考虑伸缩、横移、浮沉、侧滚、点头、摇头6 个刚体自由度。

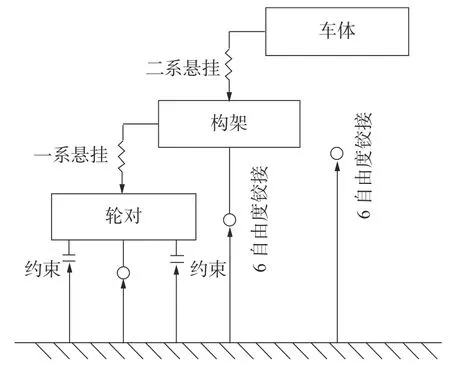
图4 动力学拓扑Fig.4 Dynamic topology

通过对车轮脱轨的动态分析，弹性变形能更合理反应出车轮形态，同时因为需要考虑高频振动反应产生的影响，建立柔性轮对以及划分轮对的实体3D 网格；随后，如图5 所示，在有限元ANSYS 软件中展开了对轮对的模态分析工作，将其进行了柔性化处理。表3 为建立的柔性轮对计算的前36 阶模态频率。

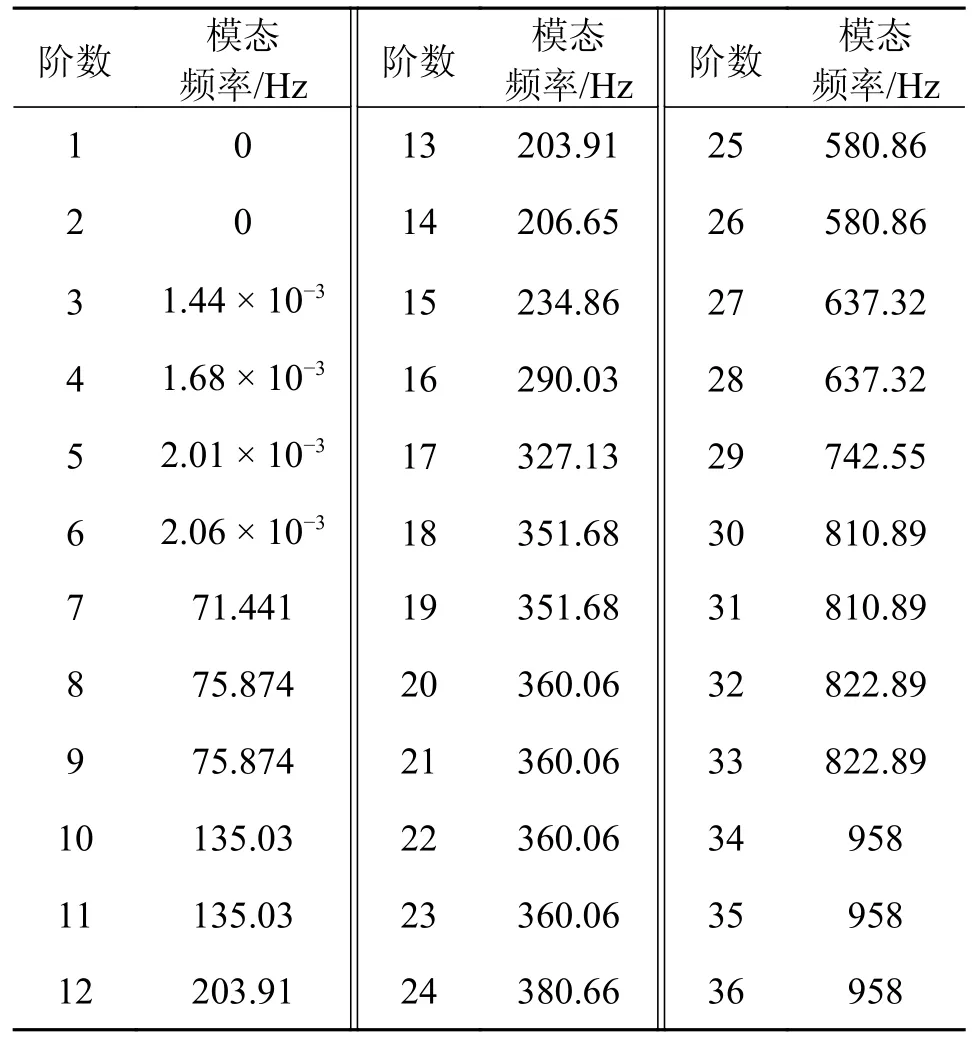
表3 轮对前36 阶模态频率Tab.3 ANSYS solution process for wheelset modal analysis

基于多体动力学软件UM（Universal mechianism）建立柔性轮对的高速列车刚柔耦合动力学模型，柔性轮对的导入通过接口模块UM FEM 实现，流程方式如图6 所示。

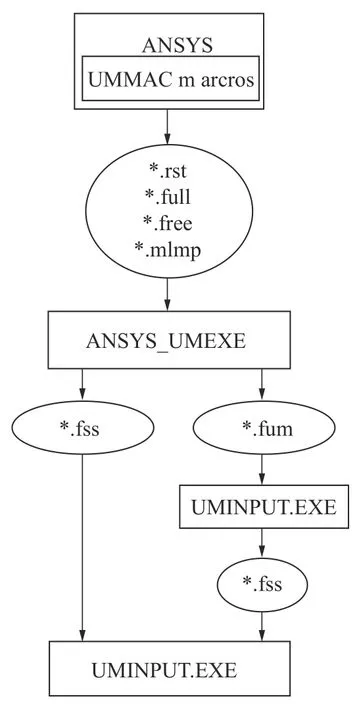
图6 ANSYS 与UM 联合建模流程Fig.6 ANSYS and UM joint modeling process

在UM 中，建立了基于柔性轮对的高速列车刚柔耦合模型，刚柔耦合动力学模型建立流程如图7所示。车体、构架、轮对均考虑横向、垂向、纵向、点头、摇头和侧滚6 个方向的自由度。

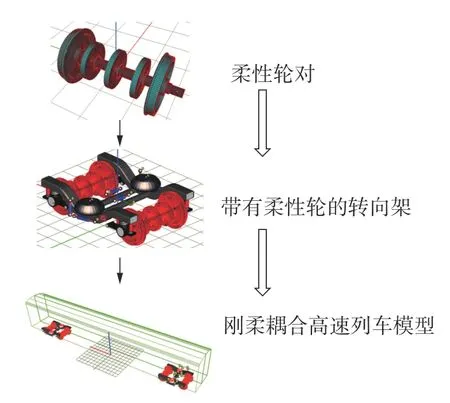
图7 刚柔耦合动力学模型建立流程Fig.7 The process for establishing a rigid-flexible coupled dynamic model

3 仿真分析

仿真分析车轮多边形与钢轨波磨轮轨综合磨耗作用下对轮轨力和振动性能的影响规律。

3.1 轮轨综合磨耗对轮轨力的影响

分析不同速度级下，对比轮轨综合磨耗和车轮多边形磨耗对轮轨垂向力的影响，设置车轮多边形阶次为20 阶，其对应幅值为0.03 mm，选取钢轨波磨波长为150 mm，其对应波深为0.01 mm。

由图8 可见，随着速度的增加垂向力也增大。在仅有车轮多边形工况下，车速每次增幅50 km/h，此时车速由原来200 km/h 到350 km/h，轮轨垂向力最大值增长幅值分别增长了2.1%、30.7%、5.9%。由图9 可见，车轮多边形对应的振动主频由385.7 Hz增加到673.8 Hz，300 km/h 速度下的振动主频576.1 Hz与轮对模态计算25 阶振型580.86 Hz 较为接近，且300 km/h 下对应的轮轨垂向力增长幅值最大，即车轮与25 阶振型模态产生共振，导致此时振动冲击增大。对比两种工况，发现在轮轨综合磨耗作用下，轮轨垂向力增长幅值更大。

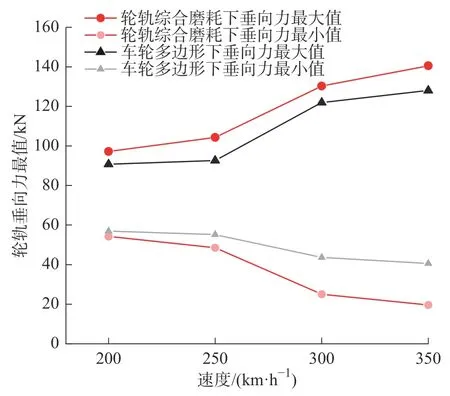
图8 不同速度下轮轨垂向力最大值对比Fig.8 Comparison of maximum vertical forces between different speeds of wheel-rail contact

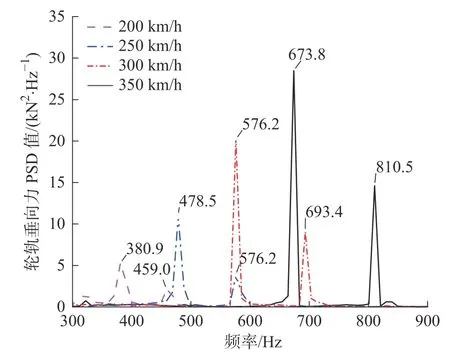
图9 轮轨垂向力频域Fig.9 The frequency domain of vertical forces at wheel-rail contact

图10、图11 给出了磨耗为20 阶，幅值为0.01 mm的车轮多边形，波深为0.01 mm 钢轨波磨，列车以300 km/h 速度运行通过不同钢轨波磨波长下对轮轨垂向力的影响规律的时频图。由图10 可知，在轮轨综合磨耗下，随着轮轨垂向力的明显增大，发生拍振现象并随着波长的减小而增大，且轮轨垂向力也出现同一规律。当波长减小至120 mm，轮轨垂向力相较于单一车轮多边形磨耗下增大了56 kN。由图11可知，轮轨垂向力的频域图中车轮多边形引起的振动频率和钢轨波磨引起的振动频率两个振动频率，且车轮多边形引起的频率所对应的振动主频的PSD 值明显大于钢轨波磨引起的频率所对应的振动主频的PSD 值。

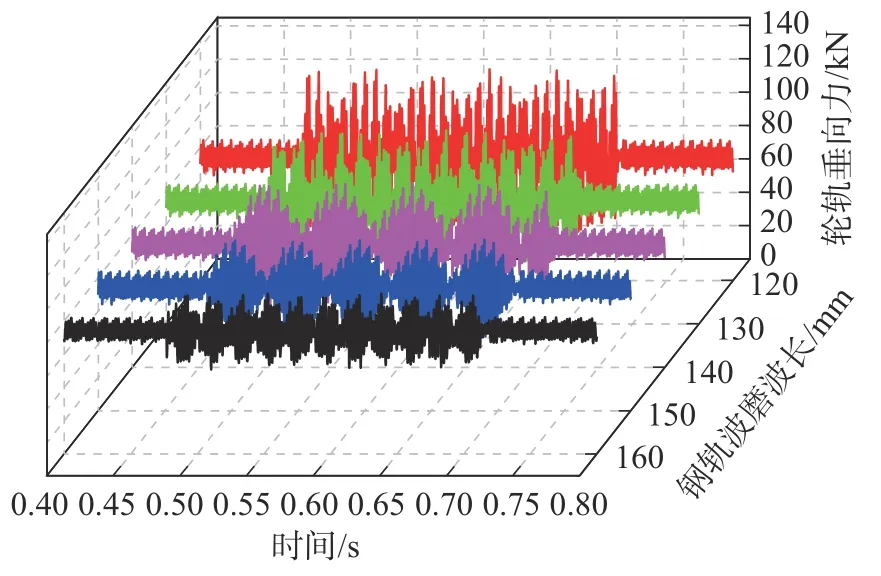
图10 轮轨垂向力时域Fig.10 The time domain of vertical forces at wheel-rail contact

图11 轮轨垂向力频域Fig.11 The frequency domain of vertical forces at wheel-rail contact

从安全角度出发，设置钢轨波磨波长为120 mm，波深为0.03 mm，分析轮轨垂向力在不同车轮多边形阶次、幅值下的变化。

由图12 可知，轮轨综合磨耗下较仅车轮车轮多边形增幅下更加明显，轮轨垂向力最大值最小增长了26 kN，最大增长了50 kN，且在阶次达到25 阶时，轮轨垂向力最大值超出170 kN，阶次为26 阶时，轮轨垂向力开始出现零值导致列车出现瞬时跳轨现象。通过对比，在不同车轮多边形阶次下，轮轨综合磨耗作用对轮轨垂向力的影响更大。

图12 不同阶次下轮轨垂向力最大值对比Fig.12 Comparison of maximum vertical forces between different orders of wheel-rail contact

由图13 可知，在轮轨综合磨耗下，轮轨垂向力大小较仅有车轮多边形磨耗工况下平均增加了23 kN，增长幅值达到6%～38%，并且当幅值达到0.05 mm，轮轨垂向力大小超过垂向力限值标准170 kN；当幅值超过0.06 mm，列车出现瞬时脱轨现象，此时轮轨垂向力最小值等于零，对列车运行安全产生威胁。即不同幅值下，综合磨耗下也对轮轨垂向力的影响更大。

图13 不同幅值下轮轨垂向力最大值对比Fig.13 Comparison of maximum vertical forces at different amplitudes of wheel-rail contact

3.2 轮轨综合磨耗对振动加速度的影响

高速列车车轮多边形与钢轨波磨对轮轨系统及列车部件振动加速度也存在一定的影响。图14～图16 给出了不同钢轨波磨波长，车轮多边形阶次对轴箱、轮对以及钢轨垂向振动加速度的影响规律。图14～图16 为振动加速度的时域图，由此可知，轴箱、轮对以及钢轨垂向振动加速度都出现拍振现象，并且拍振幅值随着波长的增大而减小。对轴箱、轮对以及钢轨垂向振动加速度最大值统计分析，由图17 可知，轴箱、轮对以及钢轨垂向振动加速度的最大值随着钢轨波磨波长的减小而增大，当钢轨波磨波长从160 mm 减小至120 mm，最大值分别增加了254 m/s2，45 m/s2，211 m/s2。即在不同钢轨波磨波长下，轮轨综合磨耗对轴箱、轮对以及钢轨垂向振动加速度的影响更大。

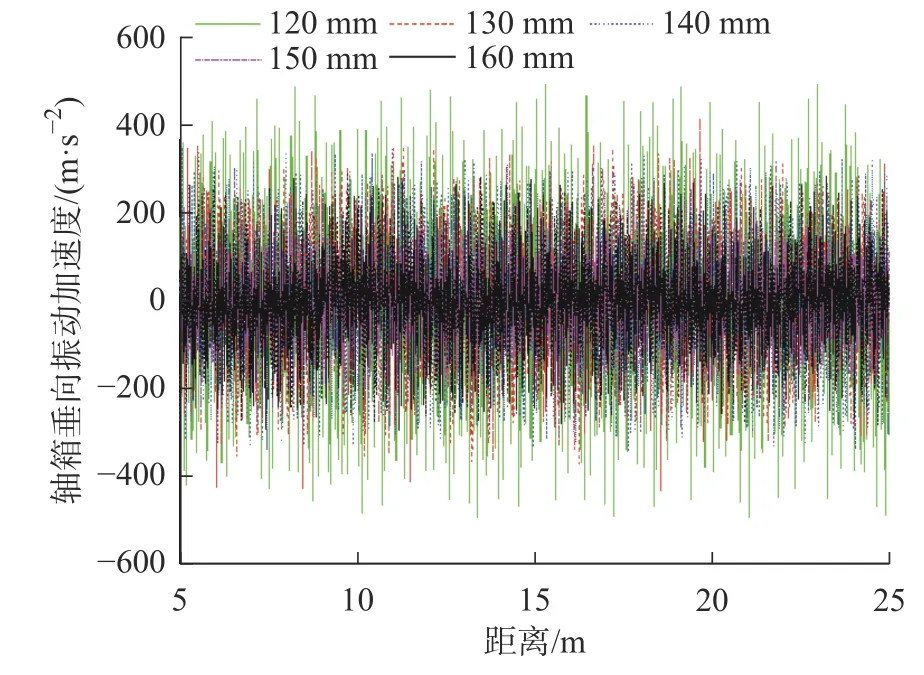
图14 轮轨综合磨耗下随波长变化的轴箱垂向振动加速度Fig.14 Axle box vertical vibration acceleration with varying wavelengths under comprehensive wheel-rail wear

图15 轮轨综合磨耗下随波长变化的轮对垂向振动加速度Fig.15 Wheel vertical vibration acceleration with varying wavelengths under comprehensive wheel-rail wear

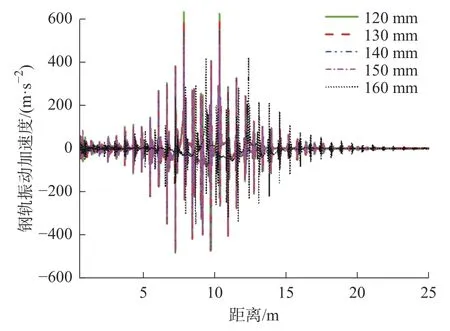
图16 轮轨综合磨耗下随波长变化的钢轨垂向振动加速度Fig.16 Rail vertical vibration acceleration with varying wavelengths under comprehensive wheel-rail wear

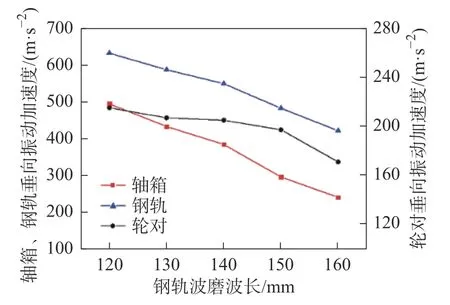
图17 轮轨综合磨耗下随波长变化的振动加速度最大值Fig.17 Maximum value of vibration acceleration with varying wavelengths under comprehensive wheel-rail wear

设置工况钢轨波磨波长为120 mm，波深为0.03 mm，列车运行速度为300 km/h，分析在不同车轮多边形阶次、幅值下的轴箱、轮对以及钢轨垂向振动加速度的变化。

图18 为不同阶次下，轮轨综合磨耗与车轮多边形磨耗下轴箱、轮对以及钢轨垂向振动加速度最大值的变化曲线的对比图，由图18 可见，轴箱、轮对及钢轨垂向振动加速度都随着阶次的增加而显著增大，尤其是轮轨综合磨耗工况下，增长更为明显，与仅有车轮多边形磨耗工况对比，阶次由10 增加至30 阶，轴箱，轮对及钢轨垂向振动加速度最大值在不同阶次下的增长幅值分别达到109%～110%，69%～102%，189%～190%，增长数值较高。所以，在不同阶次下，轮轨综合磨耗作用下对轴箱、轮对及钢轨垂向振动加速度的影响比仅有车轮多边形磨耗下更为大。

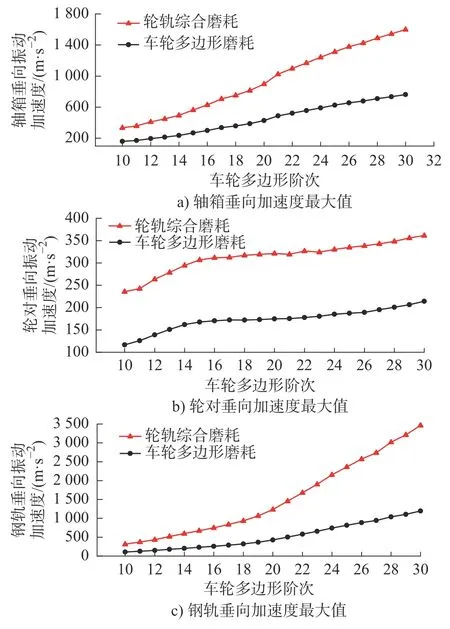
图18 不同阶次下的振动加速度最大值对比Fig.18 Comparison of maximum vibration acceleration values at different orders

如图19 所示，轴箱、轮对以及钢轨垂向振动加速度都随着车轮多边形幅值的增加明显增大。在仅有车轮多边形磨耗工况下，幅值由0.01 增至0.10 mm，轴箱、轮对以及钢轨垂向振动加速度增加了770 m/s2、456 m/s2、950 m/s2；在轮轨综合磨耗工况下，幅值由0.01 增至0.10 mm，轴箱、轮对及钢轨垂向振动加速度分别增加了1006 m/s2、449 m/s2、850 m/s2，对比仅有多边形磨耗工况，轴箱、轮对及钢轨垂向振动加速度最大值在不同幅值下分别增大了约75%～237%、25%～170%、63%～457%。即在不同幅值下，轮轨综合磨耗作用对轴箱、轮对以及钢轨垂向振动加速度的影响较仅有车轮多边形磨耗下大，且增幅明显。

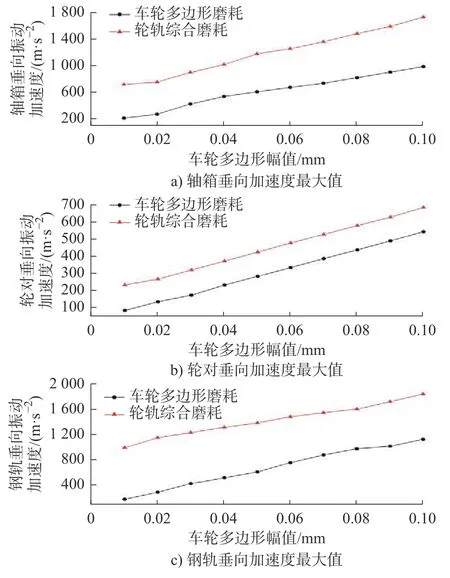
图19 不同幅值下的振动加速度最大值对比Fig.19 Comparison of maximum vibration acceleration values at different amplitudes

3.3 轮轨综合磨耗的安全限值

根据前文的仿真分析研究，从安全角度出发，设置工况多边形阶次保持在20 阶，采用降速和增加幅值两种方法的结合，计算出在轮轨综合磨耗以及车轮多边形工况的各个速度下所对应的到限幅值。其中轮轨综合磨耗含有的钢轨波磨波长为120 mm，其对应波深为0.03 mm。

不同速度级下的多边形幅值限值如图20 所示。由图20 可知，阶次20 时，随速度的增大，其对应的多边形幅值限值逐渐减小。不同速度级下，轮轨综合磨耗对应的多边形幅值限值对比仅有车轮多边形磨耗下更小。轮轨综合磨耗下相比于车轮多边形磨耗下多边形幅值限值降低25.6%，以轮轨垂向力170 kN 为安全标准，列车运行速度在300 km/h为例，20 阶车轮多边形对应的幅值限值降低了37.5%。

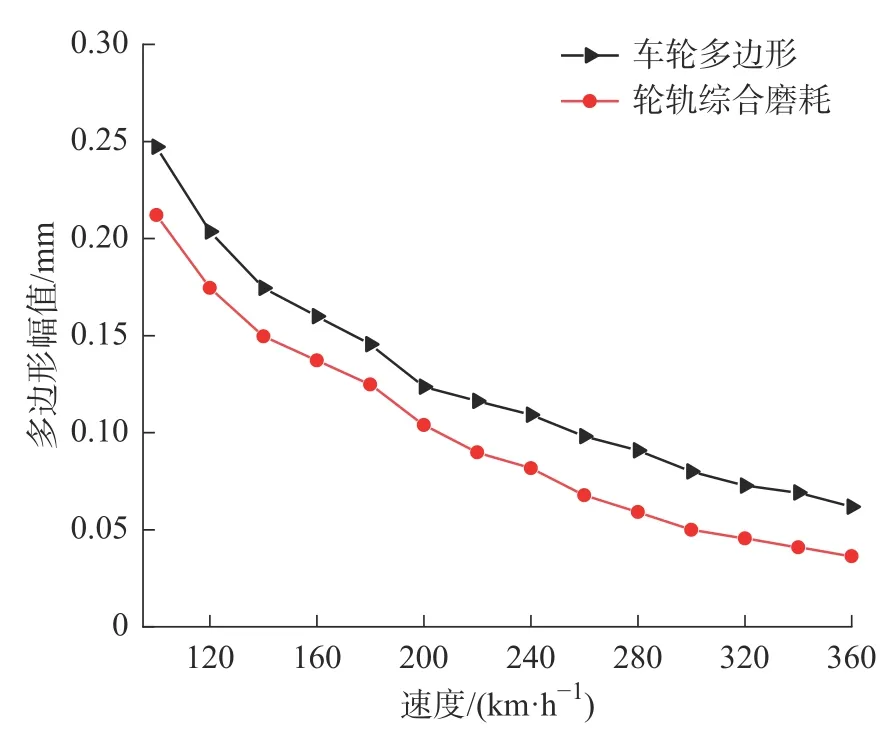
图20 不同速度级下的多边形幅值限值Fig.20 Polygon amplitude limits at different speed levels

仿真分析车速为300 km/h，轮轨综合磨耗作用下，给出如图21 所示的不同钢轨波磨波长120～160 mm分别对应的多边形阶次和幅值的安全限值。

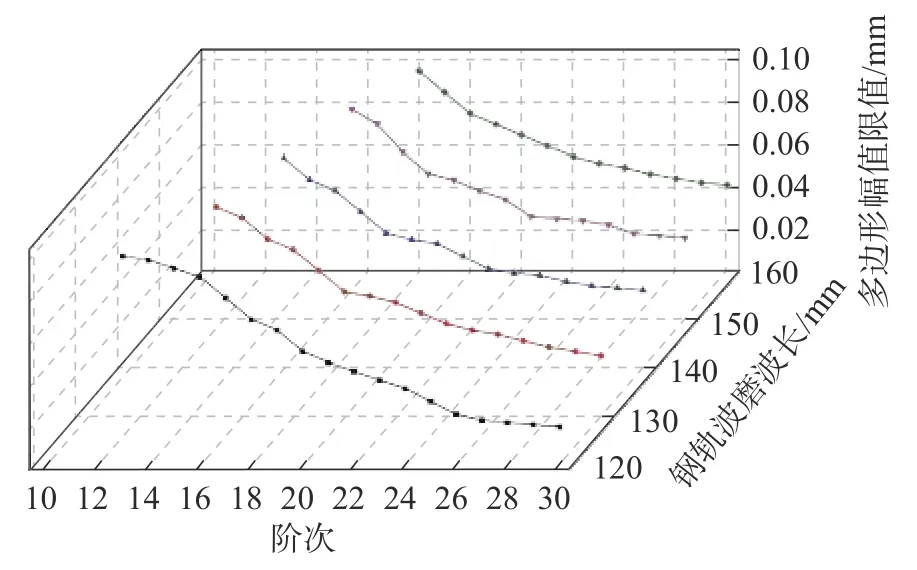
图21 不同波长、阶次下车轮多边形幅值限值Fig.21 Polygon amplitude limits at different speed levels

由图21 可知，波长为160 mm，车轮多边形阶次在18～30 阶次超出轮轨垂向力170 kN，对应的多边形幅值限值为0.042～0.100 mm；波长为150 mm，车轮多边形阶次在17～30 阶次超出轮轨垂向力170 kN，对应的多边形幅值限值为0.040～0.100 mm；波长为140 mm，车轮多边形阶次在16～30 阶次超出轮轨垂向力170 kN，对应的多边形幅值限值为0.038～0.100 mm；波长为130 mm，车轮多边形阶次在15～30 阶次超出轮轨垂向力170 kN，对应的多边形幅值限值为0.030～0.100 mm；波长为120 mm，车轮多边形阶次在13～30 阶次超出轮轨垂向力170 kN，对应的多边形幅值限值为0.020～0.100 mm。

仿真分析车速为300 km/h，轮轨综合磨耗作用下，给出如图22 所示的不同钢轨波磨波深0.01～0.04 mm分别对应的多边形阶次和幅值的安全限值。

图22 不同波深、阶次下车轮多边形幅值限值Fig.22 Polygon amplitude limits at different wave depths and orders

由图22 可知，当波深为0.01 mm，车轮多边形阶次在17～30 阶次超出轮轨垂向力170 kN，对应的多边形幅值限值为0.038～0.100 mm；当波深为0.02 mm，车轮多边形阶次在15～30 阶次超出轮轨垂向力170 kN，对应的多边形幅值限值为0.032～0.100 mm；当波深为0.03 mm，车轮多边形阶次在13～30 阶次超出轮轨垂向力170 kN，对应的多边形幅值限值为0.020～0.100 mm；当波深为0.04 mm，车轮多边形阶次在12～30 阶次超出轮轨垂向力170 kN，对应的多边形幅值限值为0.012～0.100 mm。

在高速列车运行时，存在轮轨综合磨耗作用下会加剧轮轨的动态作用力，对比仅有车轮多边形磨耗工况和轮轨综合磨耗工况下的安全限值，发现轮轨综合磨耗情况下会更快超出安全范围。根据以上提出的安全限值，建议及时对车轮多边形与钢轨磨耗进行镟修及打磨，保障列车安全运行。

4 结束语

本文仿真分析了在不同速度下，车轮多边形阶次、幅值，钢轨波磨波长、波深下，轮轨综合磨耗对车辆动力学性能的影响规律，并以轮轨垂向力170 kN为标准，提出了在轮轨综合磨耗下关于车轮多边形的安全限值。结果表明：

1）车速达到300 km/h 时，轮轨垂向力的增幅最大达到30.7%，其对应的振动主频576.1 Hz 与轮对模态计算25 阶振型580.9 Hz 较为接近，车轮与25 阶振型模态产生共振，使得此时振动冲击增大。在轮轨综合磨耗下，轮轨垂向力大小增长显著，出现明显的拍振现象，且拍振幅值随钢轨波磨波长的减小而增大；轮轨垂向力的频域图明显出现两个主频，分别对应车轮多边形和钢轨波磨引起的振动频率，其中车轮多边形比钢轨波磨对垂向力的影响更为明显。

2）轮轨垂向力随着车轮多边形阶次、幅值的增加而增大，尤其是在轮轨综合磨耗下增幅更加明显，其中，在阶次达到25 阶或幅值达到0.05 mm，轮轨垂向力最大值超出170 kN，阶次达到26 阶或幅值超过0.06 mm，垂向力最小值为0，列车出现瞬时跳轨现象，对列车运行安全产生威胁。

3）在不同钢轨波磨波长下，不同多边形阶次、幅值下，轮轨综合磨耗对轴箱、轮对以及钢轨垂向振动加速度的影响较仅有多边形磨耗下大，且垂向振动加速度增长数值较大。

4）在轮轨综合磨耗作用下，其对应的多边形幅值限值明显低于仅有多边形磨耗工况，整体平均降低25.9%，以列车运行速度在300 km/h 为例，20 阶车轮多边形对应的幅值限值降低了37.5%，列车更易超出限值；当速度为300 km/h，提出了钢轨波磨波长120～160 mm 以及波深在0.01～0.04 mm 范围内，车轮多边形阶次10～30 阶对应的幅值0.10 mm范围内关于车轮多边形的安全限值。