考虑磨耗及不等厚辐板的轨道车轮振动声辐射特性

刘跃杰,，文永蓬,,，周月,，吴俊汉,

（1.上海工程技术大学 城市轨道交通学院，上海 201620；2.上海工程技术大学 上海市轨道交通振动与噪声控制技术工程研究中心，上海 201620；3.西南交通大学 轨道交通运载系统全国重点实验室，成都 610031）

城市轨道车辆行驶过程中产生的环境振动噪声一直是困扰城市居民生活的瓶颈问题。由于列车在城市中穿梭的行驶速度区间一般为40～80 km/h，此时轮轨噪声在列车运行噪声中占比最大，根据产生机理的不同，一般分为滚动噪声、冲击噪声和啸叫[1]。车轮作为轮轨系统振动传递的重要载体，是轮轨噪声重要的声源部件之一，车轮的辐板形状特征及正常运行产生踏面磨耗变化对轮轨系统振动声辐射的影响不容小觑[2]。

近年来，为了获取低噪声车轮，开展了许多针对车轮的振动声辐射特性相关研究。文献[2-3]利用有限元结合边界元的方法，针对不同辐板形式，以及辐板厚度对多种类型城市轨道车轮振动声辐射特性进行了仿真分析，在轮轨等效粗糙度名义滚动圆接触点径向激励下，得到了斜曲辐板车轮、双S 型辐板车轮以及不同厚度下的直辐板车轮的振动声辐射特性，并总结了辐板形式和厚度对车轮声辐射的影响规律。刘林芽等[4]从轨道车轮的半径、辐板厚度和踏面质量出发，采用控制变量法研究了3 种参数对车轮振动声辐射的影响，得到了不同类型的轨道车轮的声压级响应曲线，归纳总结了3 个参数对轨道车轮振动声辐射特性的影响规律。Fabre 等[5]研究了轨道声学表面对轨道车轮声辐射的影响，通过FBEM 半空间公式并结合试验分析验证，获得了反射表面对轨道车轮声辐射特性的影响规律。Gutiérrez-gil 等[6]考虑到辐板开孔因素对车轮声辐射的影响，对比分析了辐板开孔分布对弯曲辐板车轮和直辐板车轮的声辐射影响，通过遗传算法优化器的计算，归纳了穿孔模式下车轮声辐射变化规律。文献[7-8]从轨道车轮辐板阻尼层及其厚度出发，建立了轮轨滚动噪声预测模型，在轮轨粗糙度激励下，获得了辐板阻尼层及其厚度因素对车轮振动声辐射特性的影响规律。总之，目前多数对轨道车轮振动声辐射特性的研究[9-11]往往将辐板厚度作为单一变量进行研究，并未充分重视辐板不等厚特征对车轮振动噪声带来的影响，根据长期服役引起的踏面磨耗情况，针对不等厚辐板车轮振动噪声研究尚需进一步探索。

课题组前期在轨道车轮辐板应力拓扑优化、热力耦合拓扑优化方面的研究工作表明，不等厚辐板车轮在改善车轮结构性能方面具有很好的效果[12-17]。为了进一步地结合踏面磨耗因素获取降噪车轮特征，详细讨论轨道车轮踏面的磨耗、辐板的不等厚特征对车轮振动声辐射影响的研究十分必要。为此，以城市轨道交通服役的双S 型辐板车轮为研究对象，建立反映磨耗及不等厚辐板的车轮模型，对不同类型的车轮进行振动声辐射仿真分析，形成轨道车轮振动声辐射分析流程，归纳辐板不等厚辐板及磨耗程度对车轮振动声辐射特性的影响规律，从而获得新型低噪声不等厚辐板车轮。

1 轨道车轮建模

1.1 不等厚辐板下车轮建模

双S 型辐板车轮的辐板形状呈类似驼峰状，是轨道交通领域目前服役的整体辗钢车轮之一。由于其在改善列车运行车轮受力情况方面具有更优的性能，因而被许多国家采用。上海轨道交通4 号线路采用的国产车轮ZD840，就属于双S 型辐板车轮，图1为双S 型车轮的断面模型，其材料属性详见文献[14]。

图1 双S 型车轮断面形状及辐板区域划分Fig.1 Cross-sectional shape of the double S-type wheel and division of the spoke plate region

为了更细致地研究辐板区域对于车轮的振动声辐射的影响情况，以正在服役的双S 型辐板车轮作为优化设计的初始车轮，将其辐板区域分为如图1所示的3 个部分：辐板上部、辐板中部以及辐板下部。已有研究[18]表明适当增加车轮辐板厚度可以减小车轮噪声辐射，在此基础上，分别通过增加辐板上部、辐板中部以及辐板下部辐板厚度，来研究辐板各部分对车轮总体振动声辐射影响规律。

为了兼顾车辆轻量化和降噪性能需求，控制车轮辐板增厚限制为车轮总体积提升8%，并采用辐板两侧沿轴向向外扩大的方式。另外，在连接处为了考虑到整体形状平滑过渡，保证车轮辐板形状不出现尖角类的突出结构，采用样条曲线连接过渡位置，分别建立基于辐板不同部位的不等厚辐板车轮模型，记为辐板上部不等厚车轮，辐板中部不等厚车轮和辐板下部不等厚车轮，其截面如图2 所示。

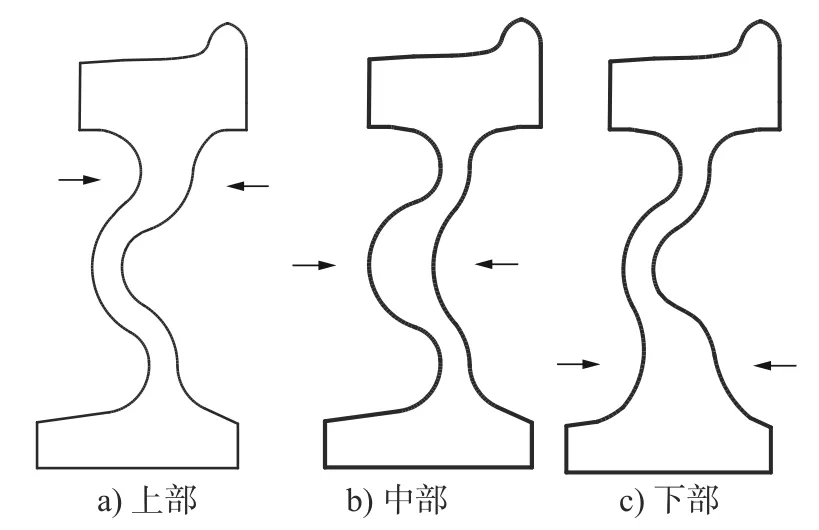
图2 不等厚辐板车轮模型Fig.2 The nonuniform thickness spoke plate wheel model

1.2 不同磨耗情况下车轮建模

为了研究初始车轮在磨耗情况下的振动声辐射情况，建立考虑不同磨耗程度下的车轮振动声辐射车轮模型，如图3 所示。

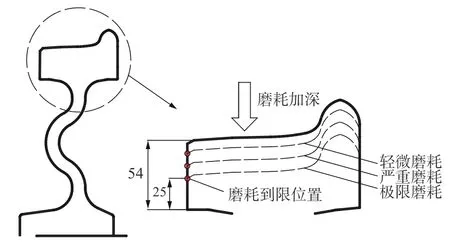
图3 车轮踏面磨耗表征Fig.3 Characterization of wheel tread wear

由于一般磨耗到限车轮的轮辋厚度为25 mm，本文以轮辋厚度25 mm 为最低限制，将磨耗程度分为3 种情况：轻微磨耗、严重磨耗和极限磨耗，进一步建立的3 种磨耗车轮模型如图4 所示。

图4 磨耗车轮模型Fig.4 The worn wheel model

2 振动声辐射分析流程

2.1 约束条件

通过仿真平台WORKBENCH 分别建立了考虑磨耗情况及不等厚辐板的车轮有限元三维模型，对不同类型的车轮进行振动声辐射特性分析。

以辐板上部不等厚车轮为例，其三维有限元网格模型如图5 所示。该模型采用空间八面体单元划分网格，该网格模型可达129 760 个单元和200 244个节点，可以满足计算精度的要求。

图5 辐板上部不等厚车轮三维有限元网格模型Fig.5 The three-dimensional finite element mesh model of upper nonuniform thickness wheels on spoke plates

图6 反映了在轨道车轮上施加约束和载荷的位置。对轨道车轮进行模态分析过程中，考虑车轮的实际运行状态，在车轮的轮毂孔内侧面上施加全约束（标记为A处）。轮轨噪声产生的直接原因是由于车轮和钢轨接触面不平顺，即轮轨不平顺引起了轮轨噪声，本文在施加轮轨激励时，采用轮轨粗糙度等效力法施加轮轨载荷激励，使用的粗糙度谱详见文献[19]。考虑轮轨垂向输入对车轮振动声辐射特性的影响，因此，载荷激励具体的施加方式为：轮轨粗糙度等效力沿垂向施加在车轮踏面轮轨接触点处，模拟车轮在列车70 km/h 速度下直线运行的工况，在三维车轮中的施加效果如图6 所示（标记为B处），载荷施加的具体位置如图7 所示。

图6 约束和载荷的位置Fig.6 Positions of constraints and loads

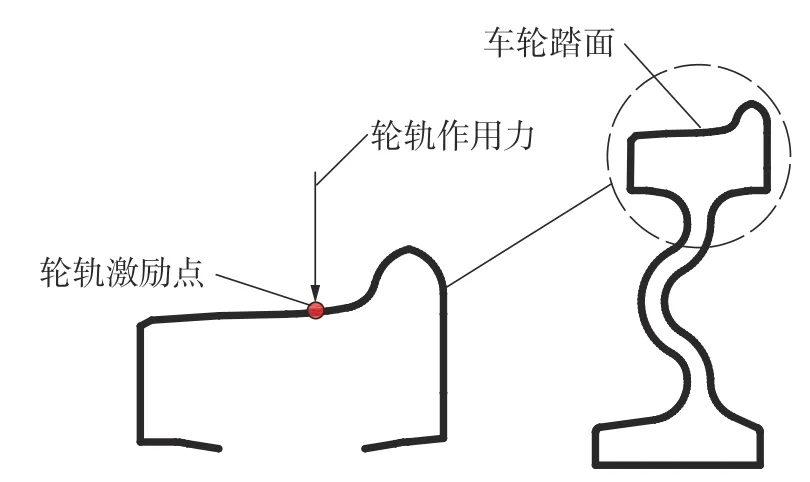
图7 轮轨激励位置Fig.7 The Position of wheel-rail excitation

2.2 分析流程

图8 为车轮声辐射仿真过程中选取的空气域大小，施加空气域的目的是模拟城市轨道车轮实际工作所处的空气环境，这是声辐射分析设置重要的一步。采用空间立方体空气域结构，设置空气域尺寸为：从车轮轴向和径向结构的最远端向外扩展200 mm 为空气域的包络尺寸，如图8b）和图8c）所示。对结构声辐射水平的评价，声压级作为结构声学中一项噪声指标会受到声源与辐射面距离的影响，而声功率则只与结构本身的物理属性有关，也通常被用来评定城市轨道车轮的噪声水平。因此，论文从结构降噪的角度出发，选用噪声声功率级作为轨道车轮声辐射水平的评价指标。

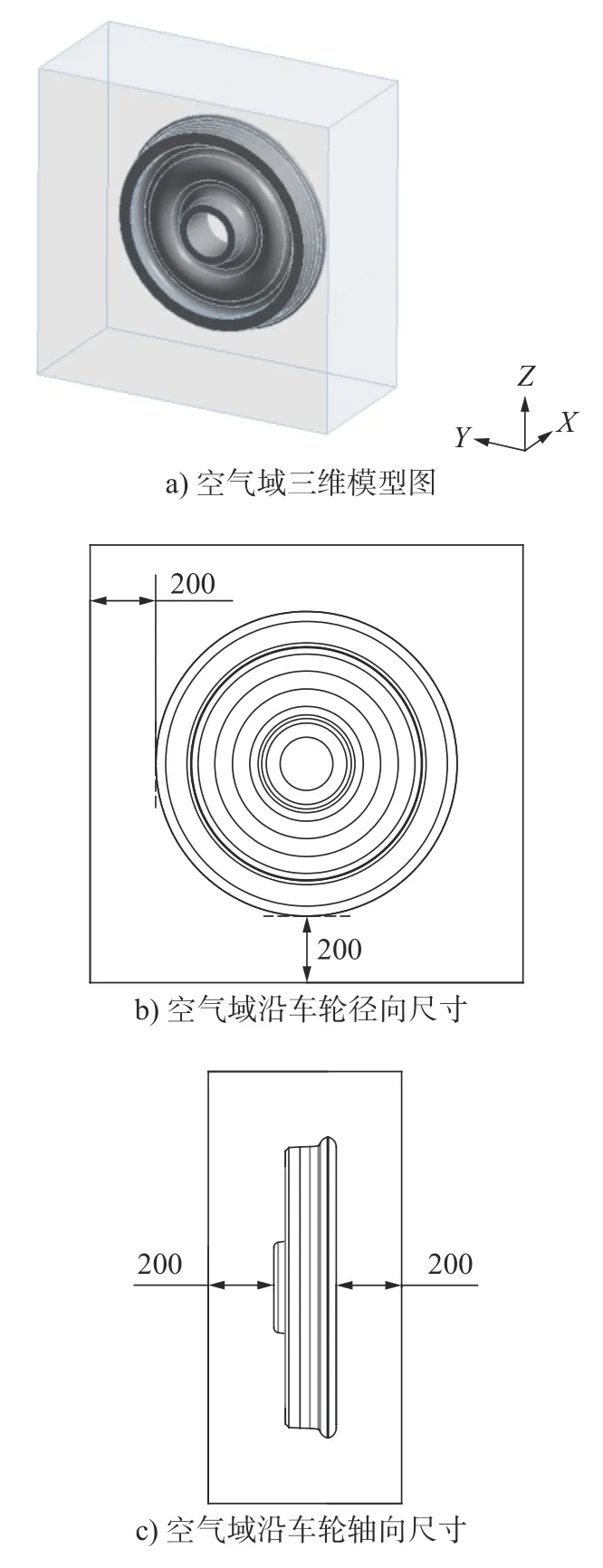
图8 Enclosure 空气域Fig.8 Air domain of the enclosure

图9 为轨道车轮声辐射仿真流程图。由图9 可知：首先将轨道车轮模型导入WORKBENCH 声学分析平台之后，首先要对车轮设定相应的材料属性，这是车轮有限元分析的基础；然后利用Enclosure 建立车轮声学分析空气域，并且根据车轮和空气域的形状特征采用空间六面体单元划分网格，采用合适的单元类型以及网格划分方法是声辐射分析的关键步骤；最后指定物理结构区域和声辐射区域，对车轮施加约束和载荷，这是区分研究对象和外部环境的重要一步，声辐射仿真后处理部分选择提取车轮的辐射声功率级曲线。

图9 轨道车轮声辐射仿真流程图Fig.9 Simulation process for wheel-rail acoustic radiation

声辐射计算过程中，取车轮所处的空气密度d=1.225 kg/m3，空气中声音的传播速度c=346.25 m/s，各向同性热导率k=0.024 2 W/K，比热容C=1 006.4 J/(kg·K)，动力黏度f=1.78×10-5N·s/m2。另外，设置声学求解频率区间为0～5 000 Hz，计算步长为40 Hz。

3 结果分析与讨论

3.1 不等厚辐板车轮分析结果

对轨道车轮进行模态分析，能够获得不等厚辐板车轮以及磨耗车轮的各阶振动模态固有频率以及对应的模态振型，以此可以进一步查看不同车轮易受外界干扰的频率分布，以及车轮不同结构处振动变形的特点。使用有限元平台WORKBENCH 对不同辐板厚度的轨道车轮进行模态分析，采用Lanzos法计算提取车轮前50 阶固有频率及模态振型[7]。

轨道车轮的结构属于空间旋转体结构，因此振动的形式和圆盘结构有相似之处，可以分为轴向模态振动、径向模态振动以及周向模态振动，并且以节圆的个数m和 节径的个数n来区分同一形式振动模态下不同的振动情况。

节圆的个数m表 明沿着车轮任意径向方向的轴向振幅的分布状况，节径的个数n表 明沿着车轮圆周方向径向振幅的分布状况，因此轴向模态可表示为(m,n)，径向模态可表示为 (r,n)，周向模态可表示为(c,n)，r和c分别表示径向和周向振动情况。

表1～表3 列出了初始车轮与3 种辐板不等厚车轮在0～5 000 Hz 频率范围内的固有频率分布，由表1～表3可知，由于车轮体积的增加，3 种辐板不等厚车轮的各阶固有频率相比于原双S 型车轮均有所增大。

表1 不等厚辐板车轮轴向振动模态的固有频率Tab.1 The natural frequency distribution of wheel axial vibration modes Hz

表2 不等厚辐板车轮径向振动模态的固有频率Tab.2 The natural frequency distribution of wheel radial vibration modes Hz

表3 不等厚辐板车轮周向振动模态的固有频率Tab.3 The natural frequency distribution of wheel circumferential vibration modes Hz

图10 为初始车轮和其他3 种辐板不等厚车轮模型的声功率曲线响应对比图。由图10 可知，相比于初始车轮，其他3 种辐板不等厚车轮模型在声功率级响应上产生了较明显的差异，其中初始车轮的峰值声功率级发生在频率位置1 960 Hz 处，大小为112.66 dBA；辐板上部不等厚车轮的峰值声功率级发生在频率位置840 Hz 处，大小为98.84 dBA；辐板中部不等厚的峰值声功率级发生在频率位置1 720 Hz处，大小为115.49 dBA，辐板下部不等厚车轮的峰值声功率级发生在频率位置3 120 Hz 处，大小为110.65 dBA，从峰值声功率级来看，辐板上部不等厚车轮的峰值声功率级相比于初始车轮降低了13.82 dBA，而辐板中部不等厚车轮提高了2.83 dBA，辐板下部不等厚车轮降低了2.01 dBA，说明辐板上部不等厚车轮相比于初始车轮在峰值声功率级上有较明显减小，具有更低的噪声辐射特性，而辐板中部与下部不等厚车轮在声功率级上与初始车轮基本一致，变化不大。

图11 为频率840 Hz（如图10 中的虚线位置）附近的辐板上部不等厚车轮与初始车轮的结构振型对比，由图11 可知，在840 Hz 频率附近辐板上部不等厚车轮的典型模态振型为径向模态振型（r,1），如图11a）所示，而出现在该频率附近的初始车轮的典型模态振型（见表2）也是径向模态振型（r,1），如图11b）所示，在该种类型的模态振型情况下，车轮的总体振动位移主要体现在车轮径向方向，节径的个数为1，其中轮辋和辐板上部区域的振动位移最为突出，辐板上部不等厚车轮较初始车轮在辐板上部区域进行了加厚，辐板上部结构的刚度有所增加，一定程度上抑制了车轮的径向振动，因此辐板上部不等厚车轮在此频率处的噪声要比初始车轮小一些。

图11 车轮在径向模态（r,1）下的结构振型Fig.11 Structural mode shapes of the wheel in radial mode (r,1)

3.2 磨耗车轮分析结果

表4～表6 列出了初始车轮与3 种磨耗车轮在0～5 000 Hz 频率范围内的固有频率分布，由表4～表6可知，不同磨耗条件下的车轮基频相比于初始车轮有所增大，但总体上各阶固有频率分布大小基本一致，差异较小。

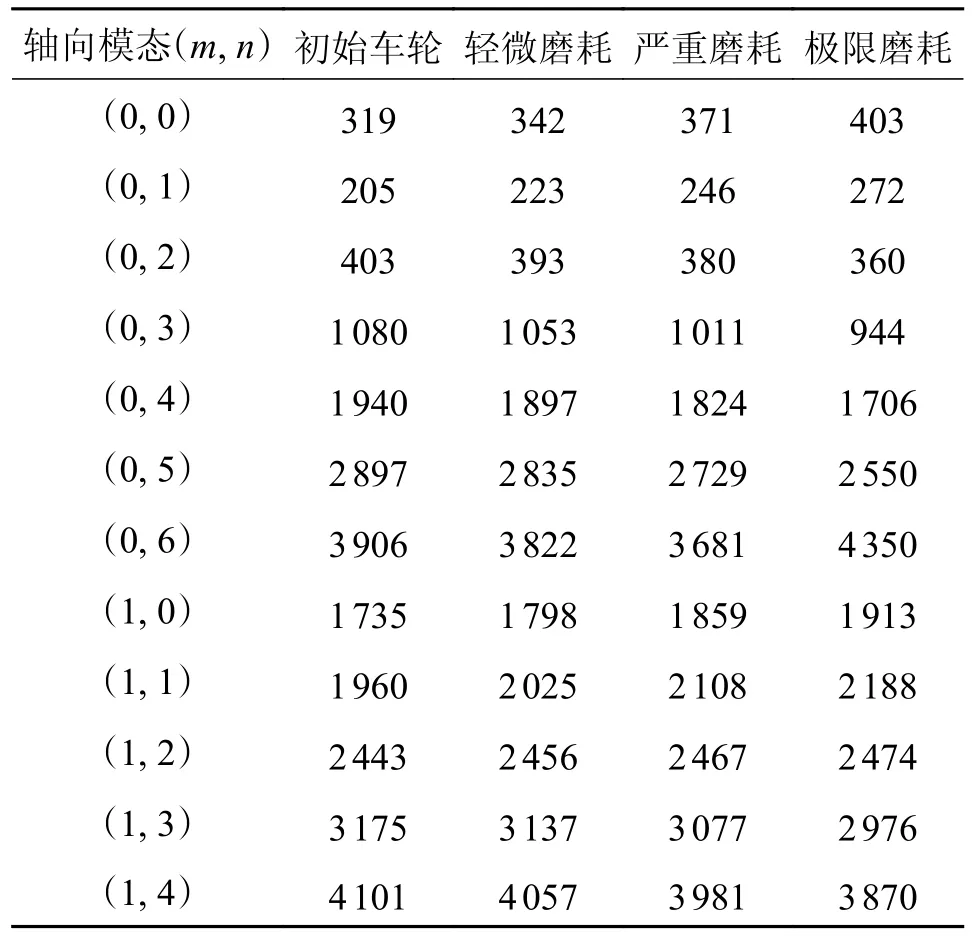
表4 磨耗车轮轴向振动模态的固有频率Tab.4 The natural frequency distribution of wheel axial vibration modes Hz

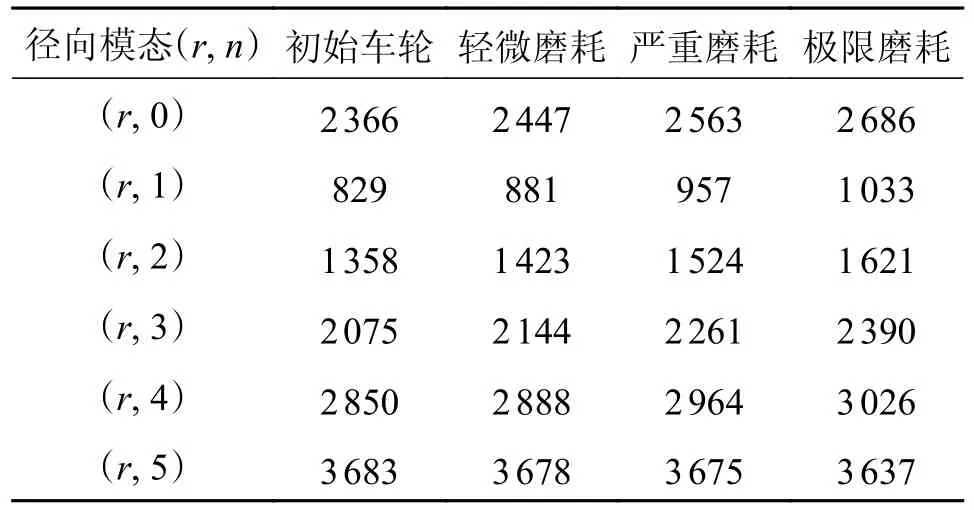
表5 磨耗车轮径向振动模态的固有频率Tab.5 The natural frequency distribution of wheel radial vibration modes Hz

表6 磨耗车轮周向振动模态的固有频率Tab.6 The natural frequency distribution of wheel circumferential vibration modes Hz

图12 为初始车轮和其他3 种磨耗车轮的声功率曲线响应对比图。由图12 可知，相比于初始车轮，不同磨耗下的车轮在声功率级响应上产生了较明显的差异，其中初始车轮的峰值声功率级发生在频率位置1 960 Hz 处，大小为112.66 dBA；轻微磨耗车轮的峰值声功率级发生在频率位置3 680 Hz处，大小为119.83 dBA；严重磨耗车轮的峰值声功率级发生在频率位置1 525 Hz 处，大小为123.78 dBA，极限磨耗车轮的峰值声功率级发生在频率位置3 630 Hz 处，大小为124.80 dBA，从峰值声功率级来看，轻微磨耗、严重磨耗和极限磨耗下的车轮峰值声功率级相比于初始车轮分别提高了7.17 dBA、11.12 dBA 和12.14 dBA，说明磨耗条件下的车轮声辐射水平均高于初始车轮，并随着车轮踏面磨耗深度的增加，车轮的噪声呈现逐渐增大的趋势。

图12 不同磨耗下车轮声功率级曲线Fig.12 Comparison of sound power level curves for the wheel under different wear conditions

图13 为频率3 630 Hz（如图12 中的虚线位置）附近的初始车轮和其他3 种磨耗车轮的结构振型对比图。由图13 可知，该4 种车轮在3 630 Hz 频率附近的典型模态振型（见表5）均为径向振动模态（r,5），车轮总体振动位移发生在车轮的辐板上部和轮辋处，由于踏面磨耗深度的增加，车轮轮辋厚度由初始车轮开始逐渐变小，极限磨耗车轮的轮辋厚度最小，达到磨耗到限位置，同时随着轮辋厚度的减小，在沿车轮径向的轮轨作用力下，轮辋部分刚度有所减小，从而加剧了车轮的径向振动，图13a）～图13d）中，轮辋部分的振动位移增大明显，这就是极限磨耗车轮在该频率处的噪声相比其他车轮要更大的原因。

4 声辐射特性校验

根据上文分析可知，辐板上部不等厚车轮相比于初始车轮具有更低的声辐射特性，因此，下面对噪声特性更优的上部不等厚车轮在磨耗情况下的噪声特性进行校验，验证其在不同程度的磨耗情况下相比于初始车轮是否仍具有优秀的降噪特性。

基于不同磨耗下建立的辐板上部不等厚车轮噪声验证模型如图14 所示，分别记为“上部不等厚轻微磨耗车轮”、“上部不等厚严重磨耗车轮”和“上部不等厚极限磨耗车轮”。

图15 为辐板上部不等厚车轮在不同磨耗下声功率级曲线对比图。由图15 可知，相比于辐板上部不等厚车轮，不同磨耗条件下对应的上部不等厚车轮在声功率级响应上产生了一定的差异。上部不等厚车轮的峰值声功率级发生在频率位置840 Hz 处，大小为98.84 dBA；上部不等厚轻微磨耗车轮的峰值声功率级发生在频率位置1 960 Hz 处，大小为101.92 dBA；上部不等厚严重磨耗车轮的峰值声功率级发生在频率位置3 480 Hz 处，大小为104.42 dBA；上部不等厚极限磨耗车轮的峰值声功率级发生在频率位置1 840 Hz 处，大小为118.10 dBA。

图15 上部不等厚车轮在不同磨耗下声功率级曲线Fig.15 Comparison of sound power level curves for upper nonuniform thickness wheels under different wear conditions

从峰值声功率级可知，磨耗条件下的上部不等厚车轮在峰值声功率级上分别增大了3.08 dBA、5.58 dBA 和19.26 dBA，即随着踏面磨耗程度的增加，峰值声功率级在不断增大，磨耗到限制情况下的上部不等厚车轮情况最恶劣，增加了19.26 dBA。

表7 为上部不等厚车轮与初始车轮在不同磨耗下的峰值声功率级对比。由表7 可知，在不同磨耗条件下，上部不等厚车轮的峰值声功率级相比初始车轮始终低于10 dBA 左右，说明在踏面磨损过程中以及达到磨耗到限时，上部不等厚车轮相比于初始车轮都有更低的噪声特性。

表7 磨耗下上部不等厚车轮与初始车轮峰值声功率级Tab.7 Peak sound power levels of upper nonuniform thickness wheels and initial wheels under wear conditions

图16 为不同磨耗下上部不等厚车轮与初始车轮的噪声发展趋势图，设定由“零磨耗”到“轻微磨耗”的阶段为磨耗初期，由“轻微磨耗”到“严重磨耗”的阶段为磨耗中期，由“严重磨耗”到“极限磨耗”的阶段为磨耗末期。

图16 不同磨耗下上部不等厚车轮与初始车轮的噪声演变Fig.16 Noise evolution of upper nonuniform thickness wheels compared to initial wheels under different wear conditions

由图16 可知，随着踏面磨耗的加深，上部不等厚车轮的噪声峰值声功率级均低于初始车轮；在磨耗初期，初始车轮随着磨耗的加深噪声增大的更快；在磨耗中期，初始车轮与上部不等厚车轮随磨耗加深噪声增大速度基本一致；在磨耗末期，上部不等厚车轮随着磨耗加深噪声增大更快，但噪声峰值声功率级仍然低于初始车轮，这说明上部不等厚车轮从降噪的角度优与初始车轮，尤其是在磨耗前中期相比于初始车轮的降噪效果更佳。

5 结论

1）上部不等厚车轮具有优秀的降低结构噪声特征。峰值声功率级相比初始车轮能够降低13.82 dBA，这是因为在峰值声功率级处，车轮辐板上部的加厚使得辐板刚度有所增加，一定程度上抑制了车轮的径向振动；中部与下部不等厚车轮在声功率级上与初始车轮基本一致。因此，从降噪的角度，在设计车轮的辐板时，建议对双S 型车轮辐板上部进行适当增厚。

2）磨耗条件下车轮噪声均大于正常情况下车轮，且随着踏面磨耗加深，车轮噪声逐渐增大，这是因为踏面磨耗导致轮辋厚度减小，轮辋刚度降低，从而在轮轨力作用下加剧了车轮的径向振动，导致噪声增大，极限磨耗下车轮峰值声功率级相比于初始车轮提高了12.14 dBA，噪声增大最为显著。

3）考虑轨道车轮的长期稳定服役，随着踏面磨耗的加剧，上部不等厚车轮始终具有优秀的降噪特性。在不同磨耗条件下，上部不等厚车轮的峰值声功率级相比初始车轮始终低于10 dBA 左右，尤其在磨耗前中期相比于初始车轮的降噪效果更佳。