机器人喷涂涂层厚度模型分析与试验研究

齐淑林，郑权，黄兆晶，王浩，何晓龙，姜代荀，周辉

（1.中车青岛四方机车车辆股份有限公司，山东青岛 266111；2.无锡中车时代智能装备研究院有限公司，江苏无锡 214174；3.华中科技大学 机械科学与工程学院，武汉 430074）

近年来，随着全球机器人技术的发展，机器人喷涂逐渐成为一项较为成熟的技术，被广泛应用于汽车、船舶、航空航天等领域[1]。机器人喷涂的关键技术包括喷涂质量和喷涂效率，其中喷涂质量主要表现为喷涂车体表面油漆层的膜厚、光亮程度以及均匀性等，而准确的喷涂模型能够对涂层厚度和均匀性进行可靠的预测，进而优化工艺参数、喷涂轨迹和喷涂厚度等[2]，因此建立一个有效且实用的喷涂模型，对喷涂机器人的进一步应用至关重要。

国内外的研究人员在该方面做了大量的工作。20 世纪90 年代，Antonio 等[3]使用数值优化算法对机器人喷涂路径进行了优化，得到了最佳的喷涂路径，另外还对涂层的均匀性进行了分析，使其能够满足均匀性要求的同时使路径最优。2010 年，Gyorfi[4]使用图形搜索技术来查找障碍物周围的最小路径，并讨论了喷枪的一些基本参数（如喷涂速度、喷枪高度、喷枪间距等）对涂层效果的影响。2019 年，Chen 等[5]采用CFD 理论中的Euler-Euler方法，对机器人（带移动喷枪）喷涂曲面的油漆厚度分布进行了数值模拟，提出了一种基于动态网格模型求解涂料沉积模型的数值方法，该方法考虑了喷涂过程中微观机理对喷涂厚度分布的影响。

综上所述，目前的研究在机器人喷涂工艺参数和轨迹规划等方面取得了一定的成果，但还存在喷涂模型的建立较为简单和考虑的因素较为单一的问题，这也使得其适用的范围往往受限。因此需要建立一个具有普适性的泛化模型，并在优化模型的同时确保其精确性。

本文从机器人喷涂工艺参数与涂料沉积厚度分布关系出发，对传统的机器人喷涂厚度模型进行分析，针对其存在的不足，提出了新的建模方式，并使用相关算法对模型的参数进行了求解。

1 无参数喷涂沉积厚度模型的分析与建立

1.1 静态涂层厚度分布模型

静态涂层厚度分布模型研究的是机器人喷枪在距离车体表面一定距离时点喷或瞬喷所形成的涂膜厚度分布规律。本文所建立的涂层厚度分布模型基于以下假设，机器人在实际喷涂过程中，涂料经喷枪雾化产生平均直径在100 μm 以下的细小液滴，这些液滴在宏观上可以认为它们在空间中连续分布[6]。

1.1.1 椭圆双高斯和分布模型

在实际喷涂作业当中使用的最多的涂层厚度模型为有限范围模型中的β分布模型[7]，其对喷涂的表面要求较低，在规则曲面、小曲率表面上拟合性能都能达到不错的效果。

实际喷涂作业中常常会在喷帽两侧施加整形气体，其得到的喷雾外形通常为椭圆形。因此目前使用比较广泛的一种模型是椭圆双β分布模型，如图1所示，为涂层椭圆分布区域。假设沿x方向和y方向有着相同的厚度分布情况，则在同一个方向上，不同的截面处β值为恒定值。

图1 涂料分布区域Fig.1 Paint distribution area

P点的涂层累积速率为

其中：

式中：坐标原点o处的涂膜生长率为最大值，即qo=qmax；β1、β2为椭圆双β模型在x向和y向的整形参数，其大小取决于整形空气压力的大小。

由于椭圆双β分布模型自身数学特性的限制，其对于复杂的数据分析拟合能力并不理想，所以本文基于高斯分布模型，提出了新的模型，即椭圆双高斯和分布模型[8]。高斯和模型因其可选择参数较多，因而也更加灵活，其基本形式为

式中：ωi，μi，σi为待辨识参数；r为喷涂点到喷涂中心的距离；N=1,2,···。当N的阶数越大，其拟合精度越高，但是N增大到一定程度对模型的拟合效果变化不明显，反而会使得模型的求解复杂度变大，故通常采用3 阶高斯和模型即可满足要求。

因此在喷涂区域A点所在的x方向截面，其涂膜厚度分布速率为

同理可得在喷涂区域B点所在的y方向截面，其涂膜厚度分布速率为

x方向下的涂膜厚度分布系数 λx，其表达式为

由于y向和x向具有相同的分布，故假设这两个方向上的涂膜厚度分布系数相等，即 λx=λy。故当x=xP时，有

按照y方向取值范围的大小比例修正该截面的高斯和模型的期望值μ 和标准差 σ，即：

由此可得椭圆双高斯和模型函数分布为

式（10）表示了椭圆喷涂区域内某一点P（x,y）的喷涂厚度。

1.1.2 曲面上喷枪模型的建立

为了让模型能够适应复杂曲面[9-10]，本文提出了一种沿曲面喷涂的喷枪建模方法，喷涂示意图如图2 所示。

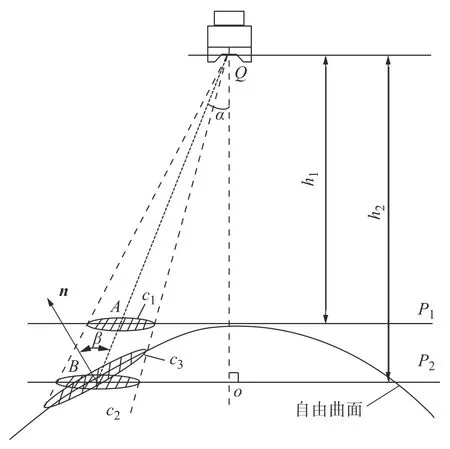
图2 曲面喷涂示意图Fig.2 Schematic diagram of curved surface spraying

假设与曲面相切的平面P1为涂膜厚度参考平面，P2为实际涂膜厚度分布平面。假设喷枪在h1和h2处得到的射流区域分别为c1和c2，对应的面积分别为S1和S2，在单位时间内涂膜厚度分别为q1和q2。由于喷涂高度的变化并不会改变涂层的生长率，根据这一特性，利用微分几何的面积放大原理[11]，可得到

设c4为与喷枪射流方向垂直的平面，c4与c2同在一个喷射角下，c3为曲面上点B处所形成的喷涂区域，也即所求的待喷涂区域。c3与c4也同在一个喷射角下，其中c3和c4在单位时间内所具有的喷涂厚度分别为q3和q4。可以求得曲面上B点处待喷涂区域的涂膜厚度关系式为

式中：x为喷涂参考平面上的点A到喷射方向喷枪中心投影点的距离；q（h，x）为点A处的涂膜厚度。

1.2 动态喷涂沉积厚度模型

1.2.1 单通道轨迹喷涂沉积厚度模型

在实际喷涂作业中，机器人通常沿某一方向连续运动，因此需要研究建立机器人连续运动的涂层厚度沉积模型。喷枪静态喷涂时所形成的喷涂区域为椭圆形，如图3 所示，喷枪沿着椭圆短轴方向喷涂比沿着长轴方向喷涂时涂料覆盖面积更大，获得的涂层也更加均匀[12]。

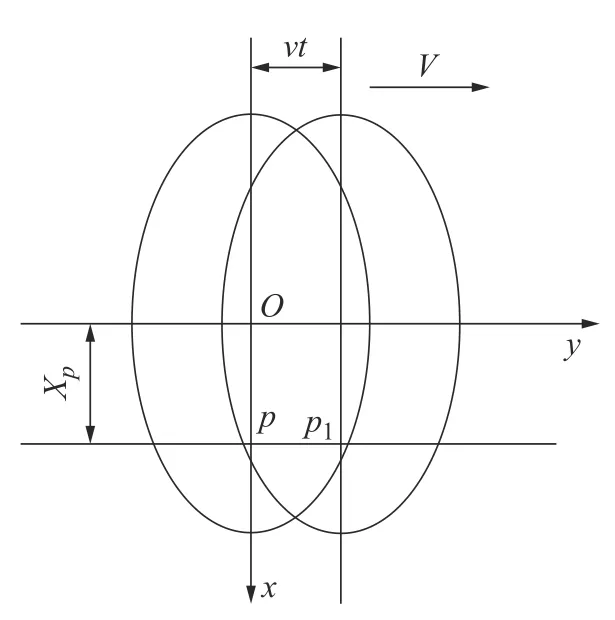
图3 单通道轨迹喷涂示意图Fig.3 Schematic diagram of single channel trajectory spraying

在某一时刻，车体上某一点P（x，y）的涂层厚度为喷枪扫过这一点的涂料累积，与喷枪经过时间有关。假设喷枪静止，点P以直线轨迹匀速经过椭圆喷涂区域所需时间是t=2b(1-)1/2/v，将x=xP,y=yP=b(1-xP/a2)1/2-vt代入式（12），则单通道喷涂过程中平面上任意点P的累计涂层厚度分布函数可以表示为

其中：

由式（13）可知，喷涂区域内任意一点的累积涂层厚度与椭圆双高斯和模型的待定参数、喷涂中心点厚度Tm、离轨迹运动中心点的距离xP、椭圆喷涂区域的长短轴以及喷涂速度v等有关。通过对喷涂时间积分，可得到单通道连续轨迹涂层厚度分布。

1.2.2 多通道轨迹喷涂沉积厚度模型

单通道轨迹涂层厚度分布是不均匀的，其效果呈现中间厚两边薄的形态。因此实际喷涂中相邻两条喷涂轨迹通常有一定的重叠距离，以确保叠加之后的涂膜厚度能够均匀一致。图4 为多通道轨迹重叠示意图。

图4 多通道轨迹喷涂示意图Fig.4 Schematic diagram of multi-channel trajectory spraying

由图4 可知，第一条喷涂轨迹涂层沉积厚度表达式为

第二条喷涂轨迹涂层沉积厚度表达式为

故重叠区域部分的涂层沉积厚度表达式为

综上，可得多通道涂层厚度表达式为：

多通道轨迹重叠后的度分布情况如图5 所示。

图5 多通道轨迹涂层厚度分布Fig.5 Coating thickness distribution of multi-channel track

2 试验验证与模型参数求解

2.1 实验平台搭建

所搭建的机器人喷涂试验平台主要包括系统硬件、电气控制系统、离线编程软件等。其中系统硬件包括机器人本体（ER5HW 机器人）、喷枪（瓦格纳W AGNER GA 4000ACEC 高压无气喷枪）、机器人控制柜、电气控制柜、高压泵等，具体如图6 所示。实验材料主要包括：喷枪、油漆、实验用铝合金侧墙样板、喷枪连接管等。测量仪器主要包括：针孔检测仪、Elcometer465 干膜厚度测厚仪、光泽度仪、涂料粘度计等。图7 为现场布置的试验设备图。

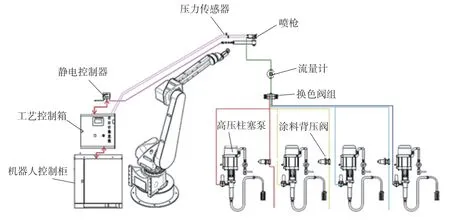
图6 喷涂机器人系统原理图Fig.6 Schematic diagram of spraying robot system

图7 试验设备Fig.7 Test equipment

图8 LM 算法原理流程图Fig.8 Principle flow chart of LM algorithm

2.2 模型参数求解及验证

为求解2.1 节所推椭圆双高斯和模型的参数，将喷枪垂直于铝合金侧墙样板进行喷涂。喷涂完毕后将所得到的椭圆喷涂区域进行划分，其中长轴方向为x轴，短轴方向为y轴，在两个轴上分别均匀取点测量漆膜的厚度，每个点重复测量3 次，然后取平均值，结果如表1 和表2 所示。

表1 x 轴方向涂膜厚度分布情况Tab.1 Film thickness distribution in x-axis direction

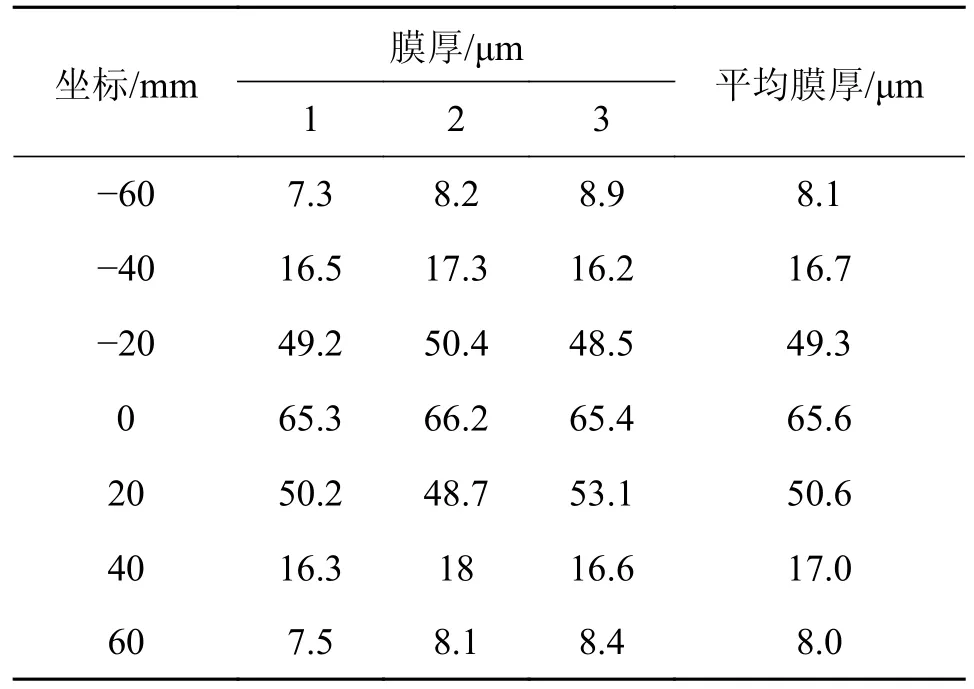
表2 y 轴方向涂膜厚度分布情况Tab.2 Film thickness distribution in y-axis direction

采用最小二乘法建立优化函数，并对表1 和表2中的测量数据进行拟合，其优化函数分别为：

将所求参数代入到椭圆双高斯和模型中，可以得到如图9 和图10 所示的静态涂层厚度分布图。

图9 x 向静态喷涂膜厚分布情况Fig.9 x-direction static spraying film thickness distribution

图10 y 向静态喷涂膜厚分布情况Fig.10 y-direction static spraying film thickness distribution

x轴和y轴方向的涂膜厚度误差分布情况如表3和表4 所示。

表3 x 轴方向模厚误差Tab.3 Film thickness error in x-axis direction

表4 y 轴方向模厚误差Tab.4 Film thickness error in y-axis direction

从图9 和图10、表3 和表4 可以看出，喷涂涂层厚度模型能够很好的拟合实际喷涂厚度分布曲线，其中x轴方向 ±80 mm，y轴方向 ±20 mm 范围内，相对平均误差小于4%，小于文献[14]建立的多变量涂层厚度分布模型所得到的4.3%的相对平均误差，并且其吻合程度高于文献[15]所建立的涂层厚度分布模型与实际涂层的吻合程度。

可以看出，椭圆双高斯和模型能够精确的模拟和预测静态喷涂时表面膜厚的分布情况，这也进一步证实了上文中所建模型的有效性。

3 结束语

本文通过分析机器人喷涂工艺参数与涂料沉积厚度之间的关系，建立了椭圆双高斯和模型，并以此为基础，进一步建立了适合曲面的喷枪模型，以及连续喷涂情况下的单通道和多通道轨迹喷涂沉积厚度模型。最后通过试验分析并求解了相关的模型参数，模拟结果证明，所建模型更加的满足实际喷涂过程，对于复杂的数据具有更好的分析拟合能力。