可重构磁耦合推进水下机器人设计与性能评估

2023-10-16李亚鑫易锦浩王宇

机械科学与技术 2023年9期

李亚鑫，易锦浩，王宇

（西南石油大学电气信息学院，成都 610500）

随着人类对于海洋探索的不断深入，水下机器人需要满足更加复杂的水下作业要求，适应更加严峻的作业环境[1]。为了提高机动性能，采用传统固定推进器的水下机器人，通常通过在不同位置增加辅助推进器的方式来提供不同矢量方向的推力，但推进器数量的增加也意味着附加质量的增加[2]。相比之下，矢量推进器同时具备推进能力和机动导向能力[3]，可以降低水下机器人对推进器数量的需求，从而在保证机动性的同时降低航行阻力和能耗[4]。

传统的矢量推进器通常利用伺服机构直接改变整个推进器的位置或者角度来提供矢量推力，这种推进器自由度有限，通常与其他导向机构或者推进器相结合。意大利弗洛伦萨大学设计的Sea-Stick系列水下机器人利用矢量推进器与船舵相结合的方式实现多自由度运动[5]。类似的，上海交通大学设计的负浮力四倾转推进器水下机器人利用倾转推进器与机翼相结合的方式提高机动能力[6]。相对的，纯矢量推进水下机器人不采用除矢量推进器以外的其他导向机构，具备更好的低速导向性能。德国吕贝克大学设计的Smart-E 水下机器人[7]，利用3 个单自由度推进器实现了全自由度推进。日本香川大学设计的球型机器人采用4 个水射流泵作为推进系统[8]，且每个射流泵都具备两个自由度的矢量偏转能力。此类推进方式虽然通过增加执行机构的方式增加了自由度和灵活性，但是牺牲了机器人的流线型外形，变相的增加了航行阻力和能耗。为了减小矢量推进产生的水文干扰，一些研究中引入并联机构来控制推进器的喷口或者螺旋桨的矢量输出方向。典型的，纽约大学理工学院设计的MASUV-1水下机器人通过偏转导管的方式改变推力方向[9]。华中科技大学设计的一种水射流矢量推进机器人采用并联机构改变射流喷口的输出矢量方向[10]。此类采用导管或者喷口的矢量推进方式虽然实现了多自由度矢量偏转，偏转扰动小，但一定程度上损失了输出动力。在实际应用中，螺旋桨作为动力输出方式更为直接有效，并且进行矢量重构时不会产生动力损失[11]，然而传统的共轴动力传输方式增加了矢量推进器的防水设计难度[12]。因此，Olivier 等[13]提出了一种基于螺旋桨推进方式的可重构磁耦合推进器，利用磁力耦合的方式实现了电机与螺旋桨之间无接触的力矩传输。在此基础上，Gasparot 等[14]测试了平面可重构磁耦合推进器实验模型的静态转矩，从实验的角度验证了这种推进器的可行性。

从现有研究来看，直接改变整体推进器方向的矢量推进器偏转扰动大，且存在多推进器执行机构冗余的问题，而采用并联机构改变推进导管或者螺旋桨的矢量推进方式存在重构范围有限和动力损失的问题。可重构磁耦合推进器在提高矢量重构能力和推进器防水性能中具有很好的应用前景，但现有设计方案仅限于数值模型或者不具备水下工作能力的单自由度推进器样机，缺乏此类推进器实际应用的综合性研究。针对这两个问题，提出了一种新型矢量推进水下机器人设计方案，该机器人搭载两个可重构磁耦合推进器构成双矢量推进系统。相较于传统鱼雷型单矢量推进水下机器人和多推进器水下机器人，该机器人通过双矢量推进器的协同作用，避免高能耗的同时具备良好的机动性能。

1 机器人结构设计

1.1 整体设计

新型矢量推进水下机器人机体上不设置除可重构磁耦合推进器以外的鳍、船舵和侧面推进器等其他辅助导向机构，仅凭借可重构磁耦合推进器产生的矢量推力来实现矢量推进和机动导向。该机器人的三维模型如图1 所示。机器人采用对称结构设计，中间为主舱体，左右两侧为可重构磁耦合推进器。为了减小航行阻力的同时最大限度利用舱体内部空间[15]，机器人主舱体设计为鱼雷型，头部和尾部设计为半球形。主舱体内部分为上下两层，上层为电气舱，用于安装控制电路板以及其他电气设备；下层为电池舱和配重舱，放置电池组和用于调节机器人浮力和平衡的配重金属块。舱体头部和尾部的空舱用于安装无线通信模块、姿态传感器和深度传感器等感知和通讯设备。主舱体上盖设有防水电气接口，用于充电和数据传输。主舱体和两侧推进器舱体通过翼形连接臂进行连接，保证连接强度，并减小阻力。

图1 可重构磁耦合推进水下机器人整体结构Fig.1 Overall structure of the reconfigurable magnetically coupled propulsion underwater robot

实验样机外形如图2 所示，机器人壳体采用光敏树脂作为主要材料，利用3D 打印技术进行制作。这种材料具备重量轻、刚度适中、精度高的优点，同时采用3D 打印技术壳体能够整体直接成型，组装部件少，可以减小机器人的结构设计难度，方便防水处理。样机基本参数如表1 所示。机器人采用负载能力更强的减速电机作为主推电机，以克服球面并联机构和磁力万向节在矢量推进中受到的阻力。

表1 实验样机参数表Tab.1 Experimental prototype parameters

图2 实验样机Fig.2 Experimental prototype

1.2 可重构磁耦合推进器

新型可重构磁耦合推进器的三维模型如图3 所示，该推进器主要由动力输出机构和变向机构两部分组成。动力输出机构包括主推电机、磁力万向节与螺旋桨，变向机构为球面并联机构。推进器通过磁力万向节将电机的输出力矩无接触地传输到螺旋桨，并且可以在不移动或者改变电机位置与角度的情况下将螺旋桨产生的矢量推力重新定向到所需要的方向，从而实现矢量推进。

图3 新型可重构磁耦合推进器Fig.3 Novel reconfigurable magnetically coupled propeller

1.2.1 磁力万向节

磁力万向节（Magnetic universal joint）作为可重构磁耦合推进器的核心部件，与传统机械万向节具有相同的功能。不同的是，磁力万向节通过磁力耦合可以进行无物理接触的扭矩传输，使得驱动电机可以完全密封，不外露传动轴，有效提高了推进器的防水性能[16]。如图4 所示，新型可重构磁耦合推进器的磁力万向节由电机侧的圆筒型转子（主动转子）和螺旋桨侧的球型转子（从动转子）两个部分组成。圆筒型转子镶嵌4 块呈筒型分布的同弧度瓦形磁铁B，球型转子镶嵌4 块呈球型分布的同弧度瓦形磁铁A。圆筒型转子通过联轴器与主推电机进行刚性连接，位于推进器防水壳内部；球型转子与螺旋桨直接连接，位于推进器防水壳外部。两个转子在磁铁的相互作用下保持一定角度的耦合状态，并且在转子中心轴线上存在吸引力，使得球型转子向电机侧靠拢，能够保证球型转子始终位于防水壳凹槽的固定位置。在水下运行时，球型转子与筒型防水外壳之间存在充满水的空腔，能够借助水的张力减少球型转子与壳体之间的机械摩擦。

图4 磁力万向节结构示意图Fig.4 Schematic diagram of the structure of the magnetic universal joint

磁力万向节两个转子的磁铁在空间中的分布情况如图5a）所示，A1～A4呈球型分布，B1～B4呈筒型分布。磁铁充磁方向如图5b）所示，相邻磁铁充磁方向相反，磁铁A和磁铁B充磁方向相对应，即N 级对应S 级，S 级对应N 级。电机通过筒型转子驱动磁铁B1～B4绕z轴旋转时，由于吸引力和排斥力相互作用，磁铁A1～A4也绕z轴以同样的速度旋转，进而通过球型转子将电机的输出扭矩传输到螺旋桨。与此同时，磁铁A1～A4相对位置不变，可以跟随球型转子绕x轴和y轴进行一定范围内的旋转，进而改变扭矩传输的方向，实现矢量推进。

图5 磁力万向节磁铁耦合示意图Fig.5 Schematic diagram of magnetic coupling in the magnetic universal joint

1.2.2 球面并联机构

两自由度球面并联机构由固定机构和偏转机构组成。固定机构包括支撑壳、伺服电机安装孔、弧形杆安装底座和螺旋桨固定轴承；偏转机构包含两个防水舵机以及两条弧形滑轨。伺服电机驱动两条弧形滑轨进行偏转，弧形滑轨通过相互滑动来带动螺旋桨轴进行偏转。

如图6 所示，弧形滑轨分别为L1和L2，对应舵机分别为S1和S2。L1和L2的偏转角度等于舵机S1和S2的输出角度，分别为a和b，以顺时针偏转为正方向，偏转范围为 [-50°,50°]。如果以螺旋桨轴为中心，将两条弧形滑轨看作两条驱动支链和两条约束支链，则可以将并联机构看作4RPc 并联机构。其中R 为转动副，Pc 为弧形滑动副。通过改变a和b的大小，该球面并联机构可以使螺旋桨具备不弱于多链路并联机构的多维矢量推进能力。

图6 两自由度球面并联机构Fig.6 The two-degree-of-freedom spherical parallel mechanism

2 动力学分析与运动规划

2.1 推进系统动力学模型

如图7 所示，以可重构磁耦合推进器的球型转子中心（矢量偏转中心）P点为原点，建立空间坐标系P-xyz，x轴与推进器轴线平行，y轴与机器人纵倾轴平行，与舵机S2的轴线重合，z轴与机器人偏航轴平行，与舵机S1的轴线重合。

图7 推力矢量分解示意图Fig.7 Schematic diagram of the thrust vector decomposition

设左推进器螺旋桨在P点产生的推力为F，则F在推进器坐标系中可以表示为

式中：Fx，Fy，Fz分别为F在x，y，z轴上产生的分力。

设 α为推力F与平面Pxy的夹角，β为F在平面Pxy上的投影与x轴的夹角，则

一般情况下，水下机器人的动力学模型可以表示为

式中：τ为水下机器人受到的驱动力和力矩，τ∈R6；M为推进器产生的合力矩。

如果不考虑水流驱动力，τ可以表示为

如图8 所示，以水下机器人浮心ob为坐标原点可以建立机器人体坐标系ob-xbybzb，G为机器人重心，xb轴正方向为机器人前进方向，yb以机器人向右横移为正方向，zb以竖直下潜为正方向。左右推进器以矢量偏转中心为原点引入推进器坐标系Pl-xlylzl和Pr-xryrzr，则推进器坐标原点Pl,Pr在体坐标系ob-xbybzb中的位置可以表示为：

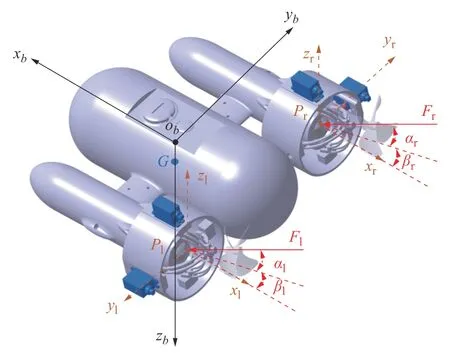
图8 机器人体坐标系和推进器坐标系Fig.8 Robot body and propeller coordinate systems

按照式（1）所述矢量分解方式，将左右推进器Pl和Pr产生的推力分别在推进器坐标系中进行分解可以得到其不同坐标轴上的分力。因此，推进器在其矢量偏转中心P点产生的作用可以表示为：

式中：Mx,My,Mz分别为推力F在x,y,z轴上产生的推力矩；l为左推进器；r为右推进器。

为了得到矢量推进器在机器人体坐标系中的推力矢量，可以对其进行旋转坐标变换。设bRp为机器人推进器坐标系到体坐标系的旋转矩阵。经过变换，推进器Pl,Pr在体坐标系ob-xbybzb中产生的作用可以分别表示为：

根据式（2）和式（5）可知，存在矩阵B∈R6×6使得

式（9）中包含了推进系统对水下机器人产生的不同驱动力和力矩，可以看出，两个可重构磁耦合推进器构成的推进系统可以为水下机器人提供6 个自由度的驱动作用。

2.2 运动姿态规划

在机械设计中，为了机身不限制螺旋桨的矢量偏转，同时考虑机身的紧凑和平衡，螺旋桨的矢量偏转中心设计在机器人尾部，使得该水下机器人的竖直面机动方式与后置单矢量推进器水下机器人类似。为了克服螺旋桨旋转产生的横向力矩，水下机器人左右推进器分别采用正桨和反桨，在实际运动控制中不考虑螺旋桨反转，即Fl,Fr≥0。在此前提下，综合两个推进器的共同作用，根据受力分析和推力矢量分解，可以对机器人的运动姿态进行规划。

机器人的基本运动姿态如图9a）～图9f）所示，蓝色箭头表示推进器产生的推力，绿色箭头表示推进器作用在机器人浮心的力矩和机器人的运动方向。当螺旋桨轴与机器人中心轴线相平行时，机器人可以进行前进或者后退的直线航行，如图9a）所示。当左右螺旋桨在竖直面偏转方向相反时，机器人可以进行横倾或者横滚的动作，如图9b）所示。当左右螺旋桨在竖直面偏转角度相同时，机器人能够进行纵倾运动，并且当力达到平衡时能够以一定倾转角进行上浮和下潜运动如图9c）和图9d）所示。当左右螺旋桨矢量在水平面偏转方向相同时，机器人可以进行偏航运动，如图9e）和图9f）所示。

图9 水下机器人的几种运动姿态Fig.9 Various motion gestures of the underwater robot

3 动力性能评估

水下机器人的航行速度和运动调节能力取决于推进系统产生的推力、力矩。为了验证水下机器人推进器分布的合理性，分析该水下机器人的实际动力性能，作者采用一种测力装置对推进系统的推力和力矩进行测试，对机器人不同自由度的动力性能进行了评估。

3.1 实验环境介绍

如图10 所示，测力装置主要包括固定支架、滑动机构、测力机构和控制电路。固定支架由铝合金方管搭建而成，用于支撑水平光杆和测力机构，整体长1 m、宽0.48 m、高0.84 m，且支架横梁可以在竖直方向进行高度调节。滑动机构包括4 条水平光杆和4 个空气滑块，测力机构通过滑块与光杆滑动连接，可以进行水平方向的直线滑动。光杆上固定有水平方向的Load cell 拉力传感器，与测力机构连接，用于测试机器人水平直线推力。测力机构通过中心轴连接机器人测试样机，中心轴同时连接动态扭矩传感器（WTN-1050E），用于测试水平面的动态转矩。控制电路采用Arduino mega2560 开发板接收传感器采集的电压模拟信号，进行A/D 转换后，通过串口将数字信号传输到PC 端进行实时统计，并通过既定公式计算出对应的转矩测试值，采集频率设置为10 Hz，每组实验进行5 次取平均值。

图10 测力实验装置Fig.10 Force measurement experimental setup

3.2 前向推力测试

水下机器人的水平前向推力是矢量推进系统能够产生的最大推力，可以评估推进系统沿机器人体坐标系的xb轴方向的动力输出能力，也是评估机器人矢量推进时推力损失率的评判基础。在进行水平直线运动时，舵机偏转角度为零，左、右推进器的推力输出相等，即al=ar=bl=br=0，F=Fl+Fr。实验中，水下机器人固定在尼龙连接支架内，通过联轴器将连接支架中心轴与测力装置中心轴连接在一起，通过改变推进器的输出率（PWM 波占空比）T，测试整体水下机器人整体产生的推力F。

令Tl=Tr∈[0,100%]，测得推进器推力变化曲线如图11 所示。可以看出，该水下机器人的推进系统能够产生的最大推力为4.4 N，在推进器输出率小于0.4 以后推力发生衰减并进入死区。从曲线可以看出，电机输出率在0.4～1 之间时，推进系统输出的推力较为稳定，可以进行平滑调速，可重构磁耦合推进器能够稳定的传递电机产生的扭矩。

图11 水下机器人前向推力曲线Fig.11 Forward thrust curve of the underwater robot

3.3 水平偏转力矩测试

根据运动规划，在进行水平转向时，螺旋桨只做水平面的矢量偏转，竖直面矢量角度为零，因此αl=αr=bl=br=0，βl=βr=al=ar=a，Fz=0，Mx=My=0。由推进系统模型式（9）可知，机器人的偏转力矩可表达为

又Plx=Prx,Ply=-Pry，所以有

表2 水平偏转力矩Tab.2 Horizontal deflection torque

由表2 可知，在舵机偏转角度a不变的情况下，水下机器人的偏转力矩Mz随着右推进器电机的输出率T的增加而增加。T不变的情况下，在a≤40°时，偏转力矩M随着舵机偏转角度a的增大而增大，当a=50°时，偏转力矩Mz变小。事实上，由推进系统模型可知，可重构推进器在进行水平偏转时，产生最大偏转力矩的偏转角度应为

右推进器力臂 |Prx|=120 mm,=100 mm，可以计算得到 |am|≈39.46°，即该水下机器在推进器水平矢量角为 39.46°时产生逆时针最大水平偏转力矩。同样的，可以计算得到推进器的水平矢量角为-39.46°时机器人产生顺时针最大水平偏转力矩。

右推进器全速推进，Tl=0,Tr=100%保持不变，改变舵机偏转角度a∈[0,50°]，测得机器人逆时针偏转力矩Mz的变化情况如图12 所示。图中虚线表示根据最大推力计算出的理论偏转力矩，实线为实验所测实际偏转力矩。可以看出，测试力矩整体略小于期望力矩，测试值在推进器水平矢量角度为 40°左右时达到最大输出力矩，最大偏转力矩约为0.69 Nm，与理论值计算值基本吻合，最大误差值约0.03 Nm，误差率不超过5%。其中，实验误差主要是由矢量偏转时弧形滑轨对螺旋桨轴的摩擦力以及测力装置本身的误差导致。因此，考虑到测量误差，机器人进行水平矢量推进时，推进系统实际推力损失率低于5%，在可接受范围内。

图12 机器人水平偏转力矩变化曲线Fig.12 Variation curve of the horizontal deflection torque of the robot

3.4 竖直偏转力矩测试

与上一节同理，进行竖直面偏转（倾转）运动时，令βl=βr=al=ar=0，αl=αr=bl=br=b，Fy=0，Mx=Mz=0。且Plx=Prx，Plz=Prz=0，所以有

因此，从理论上来说，当舵机的偏转角度设置在b∈[0,50°]时，My为正且呈递增趋势。

实验中，左右推进器的输出率T和舵机Sl1,Sr1偏转角度a不变，改变舵机Sl2,Sr2的偏转角度b，测试推进器对机器人产生的竖直分力Fz。其中T=Tl=Tr,T∈[0,100%]，b∈[0,50°]，实验测试和计算得出的部分结果如表3 所示。可以看出，机器人竖直方向的偏转力矩My的大小随着推进器输出率和舵机Sl2,Sr2偏转角度b的增加而增加，测试结果符合预期。

表3 竖直偏转力矩Tab.3 Vertical deflection torque

由于测力装置的机械性能限制，推进器输出率越高，测得分力越大，进而测试精度越高。因此以推进器全速推进为例，令T=100%保持不变，改变舵机的偏转角度b，测试并计算得到水下机器人的竖直面偏转力矩My在b∈[0,50°]的范围内变化曲线如图13所示。从图13 可以看出，该机器人的最大竖直偏转力矩约为0.359 Nm，测试值与理论值之间的误差值最大不超过0.04 Nm，误差率不超过7%。测试偏转力矩曲线变化情况与理论计算值基本吻合，即推力损失率低于7%，测试结果在可接受范围内，该水下机器人的竖直面动力性能达到理论设计要求。

图13 机器人竖直偏转力矩变化曲线Fig.13 Variation curve of the vertical deflection torque of the robot

4 运动控制测试

为了进一步验证可重构磁耦合推进水下机器人机械设计、理论分析的合理性，对水下机器人进行综合运动性能分析，且在水下机器人的运动规划以及动力性能评估的基础上，进行了水下运动控制实验。实验在3 m×2 m×1.2 m 的室外小型游泳池进行，池底和池壁各设置有测距标尺，利用相机记录实验过程，利用机载传感器记录数据，采集频率为10 Hz。通过对水下机器人直线航行、水平转向、上浮和下潜等几种基本运动进行多次测试，分析不同运动时机器人的速度、角度变化情况，对其进行综合运动性能评估。

4.1 控制系统

本设计中，机器人采用水下自主航行与水面无线遥控相结合的控制模式，控制流程如图14 所示。机器人通过深度传感器对自身所在航行深度进行检测，当航行深度进入到与地面上位机的有效通信范围内时，通过无线通信模块（ATK-HSWLDBG）与控制计算机进行数据通讯，将储存芯片内的数据传输给计算机，并接收计算机发送的任务指令。当机器人检测到航行深度超过与上位机可通讯范围，进入自主航行模式，通过深度传感器和角度传感器检测机体的运动状态，并通过PI 控制器进行运动控制计算，然后将控制信号传输到电机和舵机等执行机构，从而实现自主航行。

图14 可重构磁耦合推进水下机器人控制流程Fig.14 Control process for the reconfigurable magnetically coupled propulsion underwater robot

4.2 水平面转向测试

根据机器人运动规划与动力性能评估，按照推力测试中相同的转向控制方式，分别以推进器的推力矢量角 β=0°，10°，20°，30°，40°，对该水下机器人的水平转向性能进行测试。利用机载陀螺仪MPU9250 记录角度数据，测得机器人水平偏转角随时间变化情况如图15 所示。机器人逆时针偏转360°所需时间最短为4.7 s，角度变化曲线的斜率随机器人推进器矢量角的增加而增加，符合预期。

图15 逆时针转向角度变化曲线Fig.15 The counterclockwise steering angle variation curve

设机器人初始航向角为 0°，以 90°为目标角度进行闭环转向测试。图16a）～图16d）为机器人 90°闭环转向测试画面，机器人以推进器最大转矩输出矢量角 β=40°向目标角度进行逆时针加速转向，当机器人监测到当前水平偏转角度接近目标角度时，通过反向矢量推进动作进行减速（β∈[-40°,0°]），并最终使机器人水平转向角稳定在目标角度 90°。图17为整个闭环转向过程中水下机器人水平偏转角的变化曲线，可以看出，整个转向过程用时4.3 s，反向矢量推进动作的减速效果明显，能迅速达到目标偏转角度并最终保持稳定。

图16 90°转向测试Fig.16 90° steering test

图17 90°闭环转向偏转角度变化曲线Fig.17 Variation curve for closed-loop steering deflection angle at 90°

4.3 定向航行测试

在定向航行测试中，机器人的目标航行角与初始航行角相同，机器人保持航向角航行，当航行角度与目标角度出现差异时，利用PI 控制器进行计算，通过改变推进器矢量角度和左右推进器推力输出大小，对航向角进行实时调整。图18 和图19 分别为机器人定向航行测试画面和水平航向角的变化情况。

图18 定向航行测试Fig.18 Directed navigation test

图19 定向航行测试航向角变化曲线Fig.19 Variation curve of heading angle in the directed navigation test

图18 中标尺总长为2 m，机器人在t=0 s 时刻处于初始位置，以 0°为目标和初始航向角进行定向航行，于t=3.9 s 时刻航行至2.0 m处。过程中，机器人的平均航行速度为0.52 m/s，加速至最大速度用时不超过1.7 s，最大航行速度约为0.58 m/s。图19 为机器人定向航行的航向角变化曲线，可以看出机器人水平航向角的波动范围不超过 ±0.5°，机器人定向航行性能良好。

4.4 竖直面运动测试

在竖直面运动测试中，机器人利用深度传感器实时检测当前航行深度，利用PI 控制器进行姿态调整，当前航行深度大于目标深度则进行上浮运动，当前航行深度小于目标深度则进行下潜运动，达到目标深度以后，停止上浮（下潜）运动并保持目标深度继续航行，一定距离后停止运动并保持自由悬浮状态。实验通过机载陀螺仪、深度传感器（CJMCU5837压力传感器）和水下相机（GoPro HERO9 Black）记录机器人的倾转角度、航行深度和运动画面。

通过配重令机器人达到悬浮状态，重心与浮心重合，以机器人刚好浸没在水中80 mm 为初始航行深度，目标深度设置为450 mm。图20a）～图20d）为水下机器人自主进行下潜运动航行画面。运动过程中，机器人先以初始深度进行直线航行，检测到当前航行深度小于目标深度时，机器人头部向下倾斜进行姿态调整，达到最大倾转角时，保持倾转角进行下潜运动；检测到航行深度达到目标深度450 mm 时，螺旋桨竖直面偏转角度减小，竖直方向的推力减小，机体利用阻力和重力产生的回转力矩进行姿态回调，倾转角回调到 0°时保持目标深度继续航行。

图20 下潜运动测试Fig.20 Diving motion test

图21 为机器人下潜运动的深度变化曲线，可以看出，机器人深度从8 mm 下潜至450 mm 用时3.6 s，机器人能够快速且平稳的下潜到目标深度，到目标深度以后能够保持目标深度进行定深航行。图22 为下潜运动中机器人的倾转角变化曲线，机器人下潜运动时的姿态调整–40°所需时间约0.5 s，姿态调整时间短，能够保持机身平稳。

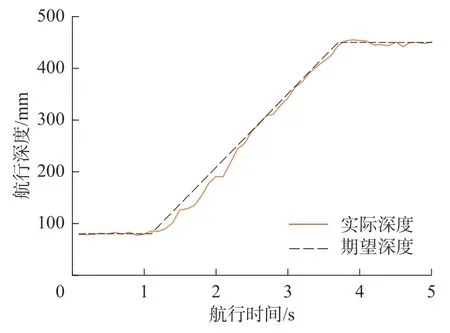
图21 下潜运动深度变化曲线Fig.21 Variation curve of depth in the diving motion test

图22 下潜运动机器人倾转角变化曲线Fig.22 Variation curve of tilt angle in diving motion

采用同样的方式，将机器人的初始航行深度设置为500 mm，目标航行深度设置为80 mm，进行自主上浮运动。图23a）～图23d）为水下t=1.1～4.2 s内的航行画面。机器人以初始深度进行直线航行，检测到当前航行深度大于目标深度时，机器人头部向上倾斜进行姿态调整，并以最大倾转角进行上浮运动；当机器人检测到当前航行深度达到目标深度80 mm 时，螺旋桨竖直面偏转角度减小，机器人进行姿态回调，机体倾转角回调到 0°时，机器人保持目标深度继续直线航行。机器人上浮运动的深度变化曲线如图24 所示，倾转角变化曲线如图25 所示。

图23 上浮运动测试Fig.23 Ascending motion test

图24 上浮运动深度变化曲线Fig.24 Variation curve of depth in the ascending motion test

图25 上浮运动机器人倾转角变化曲线Fig.25 Variation curve of tilt angle in ascending motion

由图24 和图25 可以看出，机器人深度从500 mm上浮至80 mm 总用时3.9 s，倾转角从 0°调整到40°总共用时约0.7 s，从 40°回调到 0°用时约0.5 s。机器人能够快速且平稳的上浮至目标深度，并且能够保持目标深度进行航行。上浮和下潜运动测试中，机器人最大倾转角能够达到 ±40°左右，达到最大倾转角的姿态调整时间不超过0.7 s。机器人能够自主的通过上浮或下潜运动改变航行深度，能够快速稳定地进行姿态调整，并保持目标深度进行航行。