计及幅频特性的多体受电弓参数匹配
2023-10-16王英柳玉龙陈小强
王英,柳玉龙,陈小强
(兰州交通大学 自动化与电气工程学院,兰州 730070)
电气化铁路通过受电弓与接触网之间的电气和机械接触为机车提供电能。弓网系统的动态接触性能成为影响列车运行质量进而制约列车运行速度的重要因素。随着列车运行速度的增加,受电弓系统的振动增大,导致受电弓接触压力波动增大。为了提高受电弓与接触网之间的受流质量,有必要探究受电弓与接触网之间接触压力波动的原因,并提出相应的优化方案。
文献[1]考虑了附属部件的影响,对高速铁路接触线波动速度公式进行了改进。文献[2]考虑作动器饱和,进行了受电弓主动控制器的设计。文献[3]探究了环境风对高速铁路接触线波动速度的影响。文献[4]引入“机械阻抗”的概念研究受电弓频率响应。文献[5]采用频率分析法研究了受电弓的机械阻抗。文献[6]研究了受电弓的幅频特性,分析了接触压力波动的原因,得到了线性受电弓参数与吊弦频率的匹配关系。文献[7]建立了高速受电弓的几何关系模型。文献[8]采用单目标优化算法计算受电弓最优几何参数。文献[9]基于三质量块受电弓参数灵敏度分类,采用优化算法对参数进行优化。文献[10]采用解析法分析了受电弓质量、刚度和阻尼对受电弓动态性能的敏感性。文献[11]采用单臂受电弓三质量积分模型和接触线有限元法,评价了受电弓参数对不同列车速度下接触压力的影响。文献[12]提出了考虑空气阻尼的线性受电弓频率匹配。
从弓网系统的微分方程出发,基于泰勒展开建立了弓网运动方程和垂向动力学模型;并考虑了受电弓与接触网参数相互作用的影响,分析受电弓参数与接触线参数的耦合效应及波动形成的原因,在分析结果的基础上,提出了基于阻抗匹配的改进弓网系统动态性能的优化策略,并实现了受电弓最优参数的多变量优化。
1 弓网耦合建模
1.1 接触网建模
采用模态法,将接触网看做是欧拉-伯努利梁模型进行接触网数学建模。
对接触网微分段进行受力分析,可得
式中:EI为转动刚度;ρ为该微分段线密度;T为张力;C为系统阻尼;F(x,t)为微分段所受外力大小;y为接触网的垂向位移;x为微分段水平坐标。
利用分离变量法对式(1)求解,得出承力索和接触线的振动微分方程为:
式中:qam和qbm分别为承力索和接触线相对应的第m阶模态广义位移;ρa和ρb分别为承力索和接触线的密度;L为锚段长度;U为吊弦个数;V分别为支撑杆和定位器个数;x为受电弓与接触线的接触点的位置坐标;ωam和ωbm分别为承力索和接触线的自由振动的圆频率。
式中:Fa1(x,t)和Fa2(x,t)分别为吊弦和支撑杆施加在承力索上的作用力;Fb1(x,t)和Fb2(x,t)分别为吊弦和定位器施加于接触线上的集中作用力;MA为支撑杆的质量;MB为定位器质量;MD为吊弦的质量;KA为支撑杆的刚度;KD为吊弦的刚度。
1.2 受电弓的多体模型
在实际应用中,受电弓的质量和刚度等模型参数随着受电弓升弓角度α的变化而变化。受电弓是由弓头、弓架等组成的空间结构。为简化分析,图1为其等效受电弓的多体框架模型。
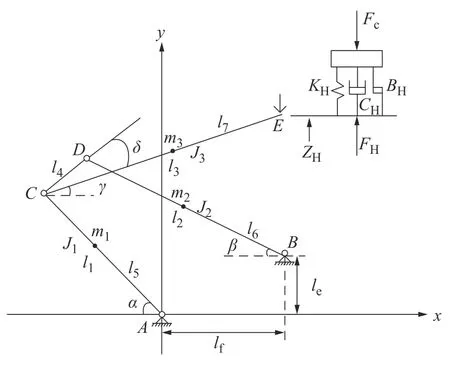
图1 多体受电弓框架模型Fig.1 The multi-body pantograph framework model
图1 中,以升弓角α作为自变量,根据拉格朗日方程,建立受电弓垂向振动微分方程,即:
式中:Ep为受电弓框架动能;Vp为对应的受电弓框架势能;Elower为下臂杆动能;ETG为推杆动能;Eupper为上臂杆动能。
将式(11)代入式(10),得到受电弓框架运动微分方程为
式中MY为升弓转矩。
在平衡位置附近对多体受电弓的运动微分方程进行高阶展开,忽略高阶项,受电弓架在平衡位置附近的等效振动微分运动为
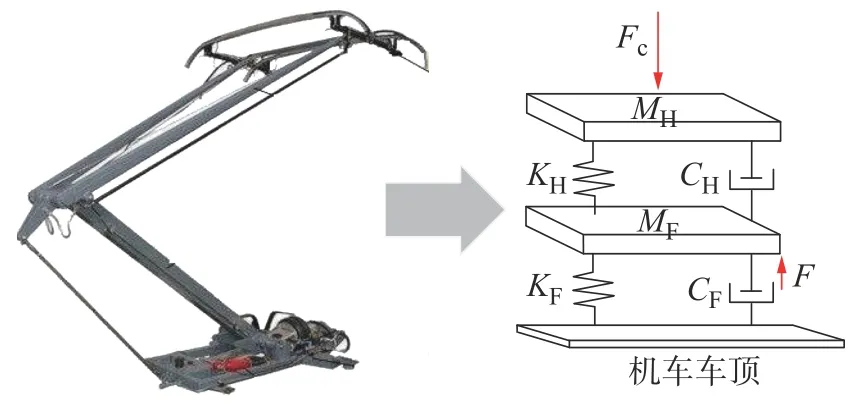
图2 受电弓等效模型Fig.2 The equivalent model of the pantograph
受电弓等效模型的动态方程为:
式中:MH和MF分别为弓头和框架的质量;KH和KF分别为弓头和框架的刚度;CH和CF分别为弓头和框架的阻尼;YH和YF分别为弓头和框架的垂向位移。受电弓无阻尼时的振动方程为:
设受电弓固有频率为λ,那么λ满足
根据式(22),计算得到
将数据代入式(23)得到受电弓的固有频率为4.74 Hz。
以兰新线CRH2 动车组为例,车顶受电弓类型为SS400+受电弓,其具体参数如表1 所示。
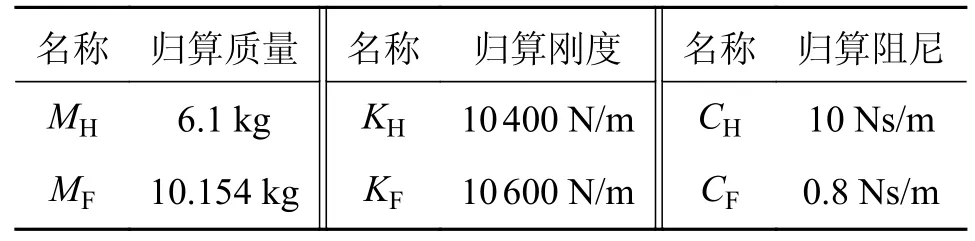
表1 SS400+受电弓的的二质量块模型物理参数Tab.1 Physical parameters of the two-mass block model for the SS400+pantograph
1.3 弓网耦合
联立式(6)~式(9)和式(20)可得弓网耦合动力学方程,受电弓与接触网间的接触压力可通过罚函数法求得。设接触刚度为Ks,则
1.4 模型验证
选欧洲标准[13]EN50318 中的弓网模型参数,建立10 跨接触网模型,列车运行速度选为250 km/h和300 km/h,接触压力通过0~20 Hz 低通滤波。表2 为模型仿真结果与EN50318 标准对比,仿真结果在标准范围内,模型可靠。
公司以经协商变更劳动合同未达成协议为由向成锐送达了解除劳动合同通知书,与成锐解除劳动合同的行为亦不符合法律规定,因此,二审法院认为,原审法院认定公司上述行为属于违法解除劳动合同,应当向成锐支付违法解除劳动合同赔偿金并无不当。公司的上诉意见与法律规定不符,对其上诉意见不予采纳。
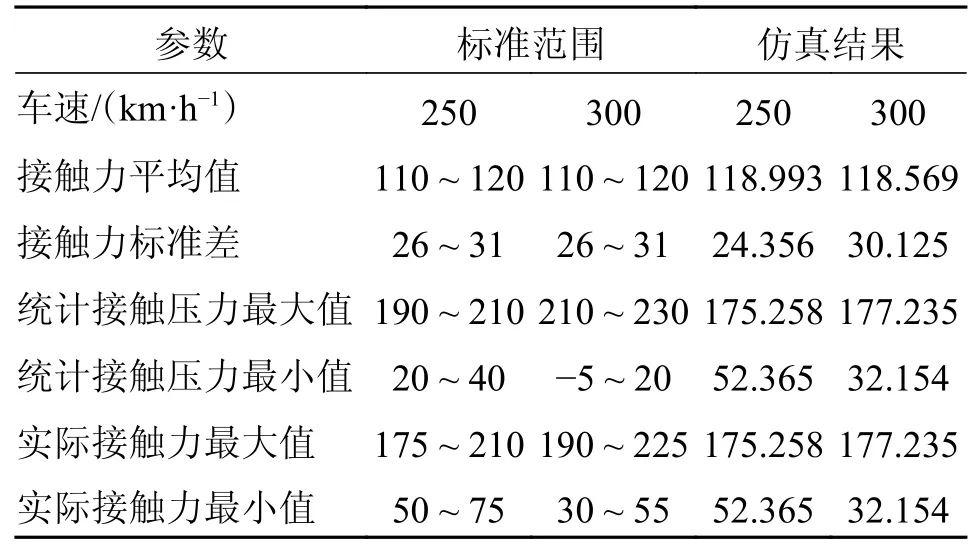
表2 仿真结果与EN50318 标准模型对比Tab.2 Comparison of simulation results with the EN50318 standard model
2 接触压力波动原因分析
当受电弓有以振幅B1、振动角频率ωb的接触线入射波波动时,受电弓的接触力变化为[14]
接触力变化振幅Fp可表示为
当接触线的波动(反向波)从受电弓运行方向前方入射时取正号,当接触线波动(行波)从受电弓运行方向后方入射时取负号。从移动坐标系看时入射受电弓的-i(1±β)ωbB1相当于接触线波动的上下速度的振幅。Z等效于接触线和受电弓耦合时的机械阻抗,由接触线和受电弓的参数决定。由式(26)可知,受电弓接触力的变化与入射受电弓接触线波动的速度振幅成正比。随着动车的运行,受电弓在吊弦处往往会产生复杂的机械波影响弓网间的接触压力大小。
由式(26)可知,在其它量不变的情况下,减小受电弓机械阻抗Zp可以减小振幅Fp,忽略升弓力F,对式(21)进行拉普拉斯变换,整理得:
受电弓的机械阻抗可以定义为接触压力的变化量和弓头速度的比值,即
式中:
令s=j·2πf,得到多体受电弓的幅频特性曲线。|H(j·2πf)|的大小表明了在该频率下的受电弓机械阻抗的大小。由图3 可以看出,多体受电弓系统的幅频响应和频率呈非线性关系,存在极小值fz1和fz2。通过分析可知如果能够调整受电弓参数使其达到合适的值,可以明显减小幅值。
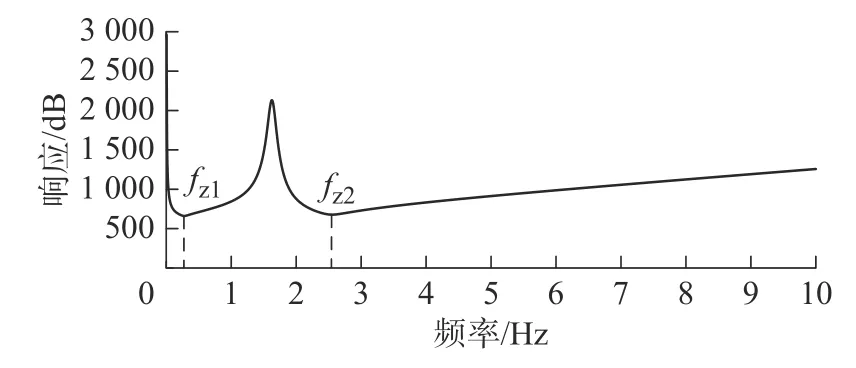
图3 受电弓幅值频率曲线Fig.3 The amplitude-frequency curve of the pantograph
3 受电弓参数的频率匹配
受电弓通过吊弦时,受电弓的抬升量发生微小的变化,通过吊弦后,受电弓抬升量逐渐变大。在跨距中间时,受电弓抬升量的周期大约为吊弦的振动周期。因此让受电弓的振动周期接近吊弦振动周期,就可以达到优化受电弓参数、减小波动的目的。本节做的工作就是改变受电弓的参数,使其转折频率fz2接近吊弦频率fd(后面讨论让fz2而不是fz1接近fd的原因)。
假设受电弓运行速度为v,接触网吊弦间距为d,吊弦距离与列车速度的比值为受电弓通过吊弦的时间,因此可定义接触网吊弦振动频率fd=v/d。以兰新高速铁路SS+400 型受电弓和CTMH150 接触网进行研究,兰新高铁车速v=200 km/h,接触网相邻吊弦间距d=5 m。根据计算的吊弦频率fd=13.88 Hz。由图3 可知fz2>fz1,易通过调整参数使fz2接近fd。
受电弓参数与受电弓机械阻抗是非线性关系,无法通过解析计算得出转折频率等于吊弦频率时受电弓参数的具体数值。但可以通过改变受电弓参数,使受电弓幅频特性曲线发生移动,从而使受电弓振动转折频率接近吊弦频率。下面通过单一变量法改变其中某个参数的值使转折频率fz2接近吊弦频率fd。
刚度对幅频特性的影响如图4 所示。受电弓质量对幅频特性的影响如图5 所示。
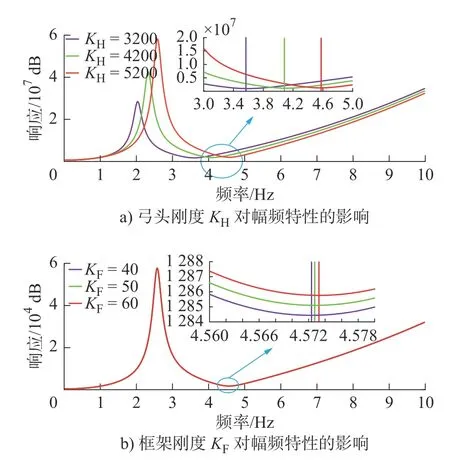
图4 刚度对幅频特性的影响Fig.4 The influence of stiffness on amplitude-frequency characteristics
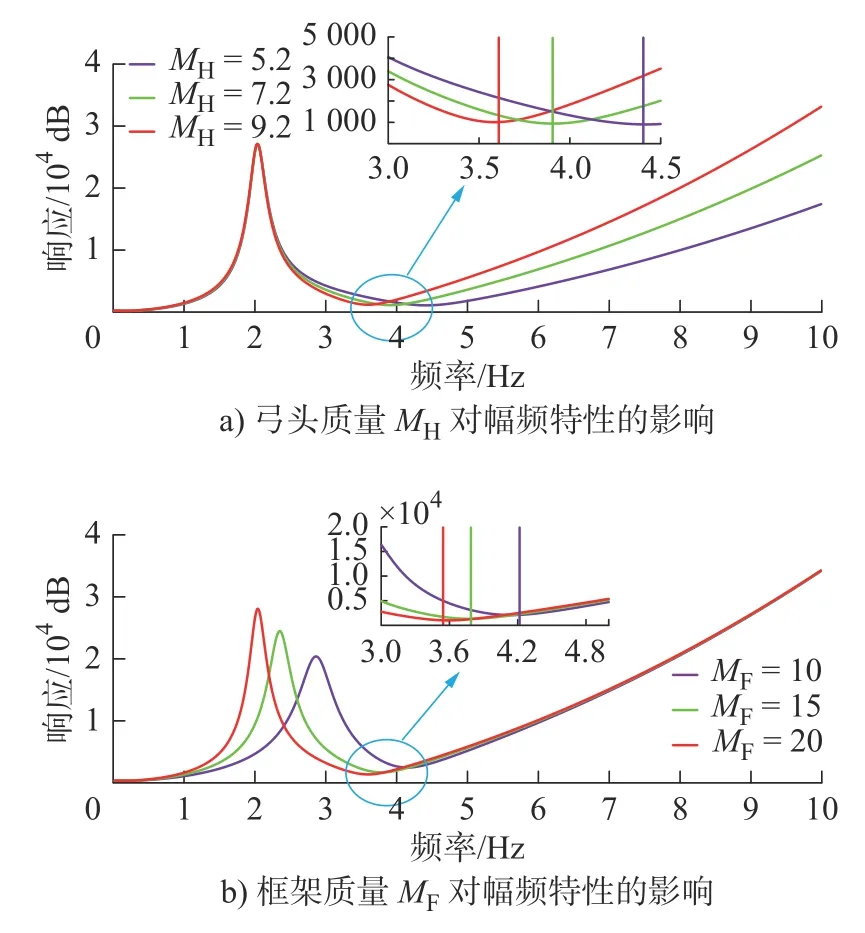
图5 受电弓质量对幅频特性的影响Fig.5 The influence of pantograph mass on amplitude-frequency characteristics
分析图4 和图5 的数据,可以得到以下结论:
1)由图4a)可知,改变弓头刚度KH,转折频率fz2变化明显,且随着KH的增大受电弓幅频特性曲线向右移动,受电弓的频率响应对KH比较敏感。
2)由图4b)可知,改变框架刚度KF,转折频率fz2对应响应增大,但转折频率fz2的数值没有明显的变化。
3)由图5a)可知,改变弓头质量MH,转折频率fz2无明显变化。
4)由图5b)可知,改变框架质量MF,转折频率fz2变化明显,受电弓的频率响应对MF比较敏感。
进一步缩小KH和MF的区间范围,得到fz2随KH和MF的变化如图6 所示。
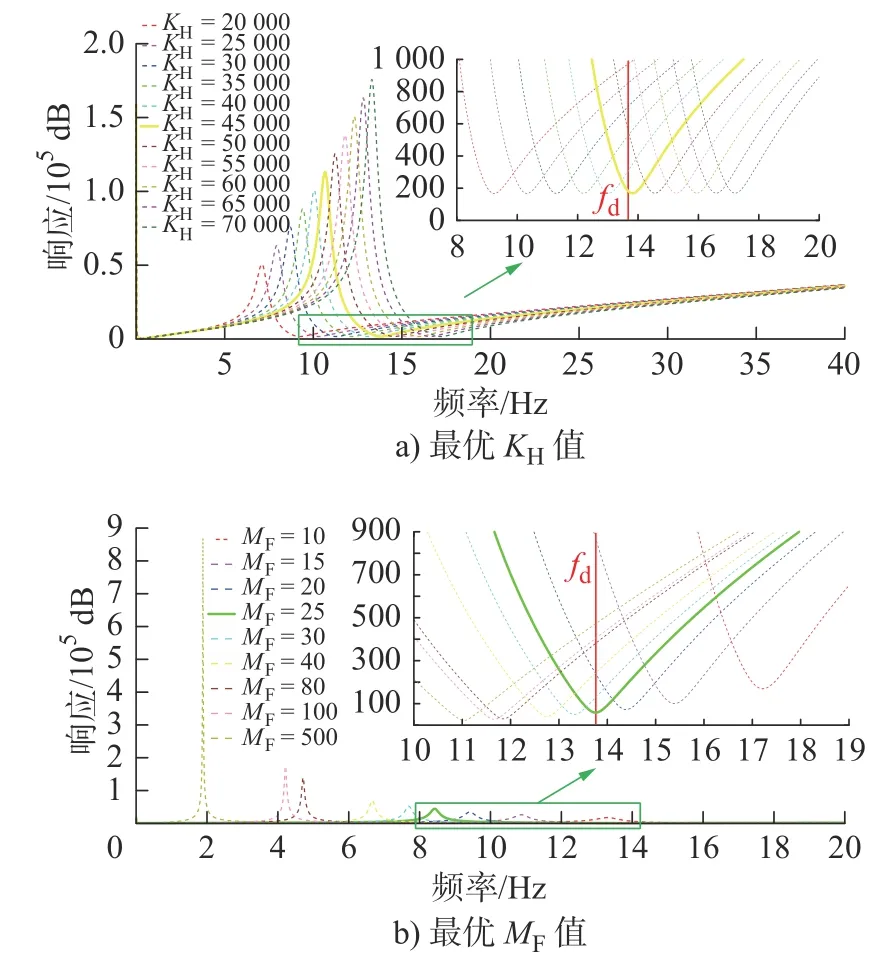
图6 最优参数值Fig.6 Optimal parameter values
当KH=45 000 时,fz2=13.816;当MF=25 时,fz2=13.757。将数据代入,仿真得到的接触压力标准差如表3 和表4 所示。由表3 和表4 可知,随着转折频率与吊弦频率的差值越来越小,接触压力标准差也越来越小。
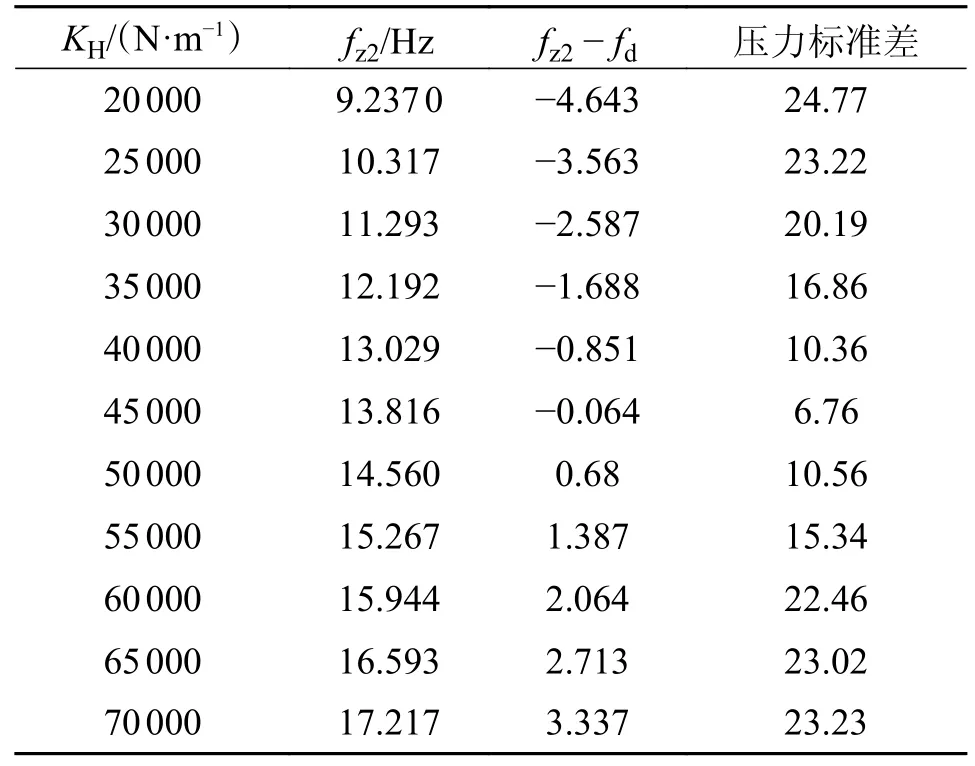
表3 不同KH 下的标准压力差Tab.3 Standard pressure difference for different KH values
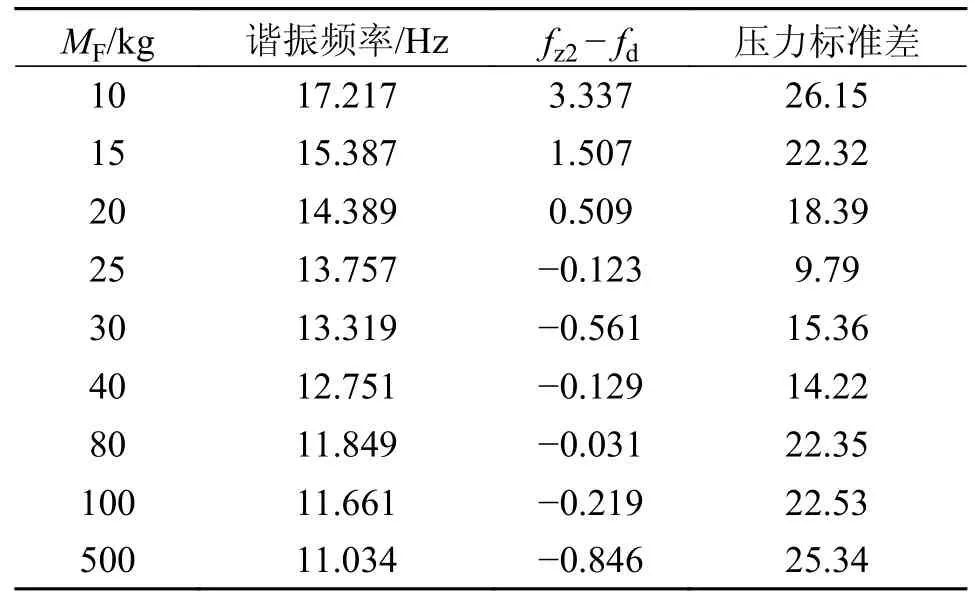
表4 不同MF 下的压力标准差Tab.4 Standard deviation of pressure for different MF values
以上是单一变量优化求取最优参数,优化后压力标准差变小。但实际的受电弓的归算质量和刚度是有范围的,达不到表3 和表4 的值,上述仿真得到的受电弓参数不能指导实际生产。且实际上受电弓的转折频率和各个参数之间是复杂的非线性关系,变量之间彼此影响,不能只考虑单变量优化,因此通过仿真数据模拟得到转折频率和两个参数之间的多项式方程,用双参数联合变化来求解最优参数。由于要找受电弓的最优的参数是fz2和吊弦频率fd匹配条件下的数值,所以要使fz2和fd的差值尽可能小,因此定义了目标函数Y=(fz2-fd)2,给定受电弓参数,仿真得出每组数据的fz2,计算出每组数据Y值,构成50 组数据集。接下来用50 组数据集进行多项式拟合得到目标函数的多项式方程的系数,用多变量优化算法得到使目标函数最小的对应的受电弓的最优参数[15]。
首先定义目标函数为转折频率和吊弦频率的差值的平方。
模拟50 组数据,得到仿真结果的二维云图如图7 所示。
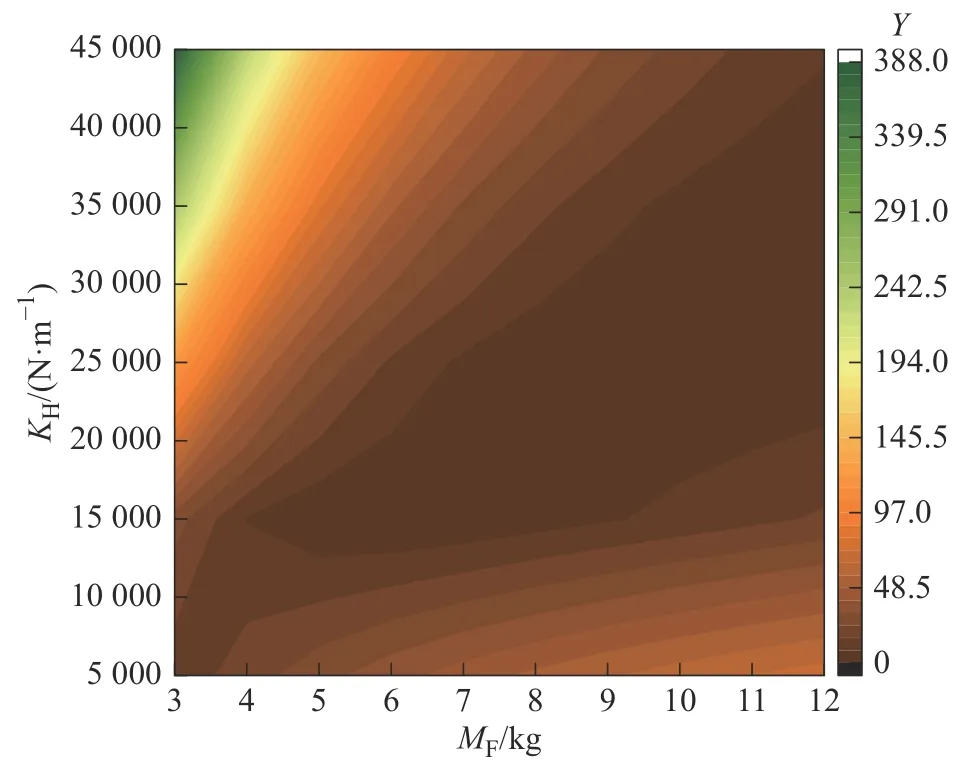
图7 目标函数的二维云图Fig.7 Two-dimensional cloud picture of the objective function
由二维云图可以看出框架质量MF越大,目标函数值越小;弓头刚度KH越小,目标函数值越小。但又不是简单的线性关系。
令目标函数Y=a0+a1MF+a2KH++a5MFKH,进行多项式拟合[15],代入数据得到a0=102.857 9,a1=-31.984 3,a2=0.003 0,a3=3.074 4,a4=0.000 0,a5=-0.001 1。所以最优匹配MF=9.7,KH=29 070。代入结果仿真得到接触压力的频谱曲线如图8 所示。
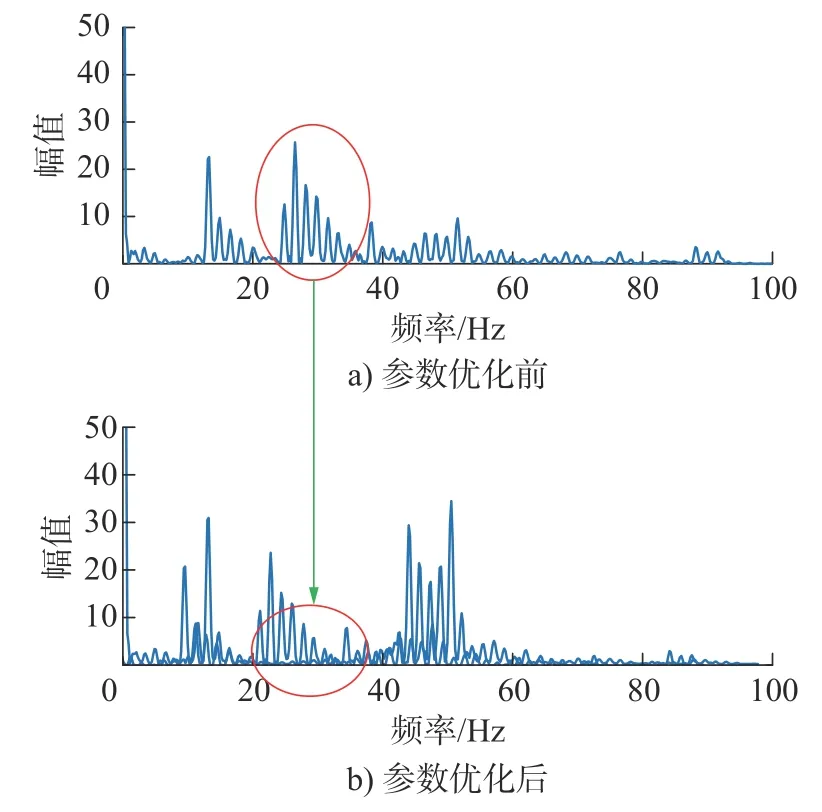
图8 频率对比图Fig.8 Frequency comparison diagram
从图8 可以看到,参数优化后吊弦频率附近10~30 Hz 范围内的响应的幅值大大降低。
4 结论
1)推导了受电弓的多体模型,在平衡位置泰勒展开,忽略高阶项,得到受电弓的动态等效模型。利用罚函数法和接触网模型耦合,得到弓网耦合模型,并对模型进行验证。
2)分析接触压力波动原因,得出减小受电弓机械阻抗可以使接触压力波动减小,提高受流质量。对受电弓微分方程进行拉普拉斯变换,得到受电弓的幅频特性曲线存在两个转折频率。
3)改变受电弓参数,以转折频率的变化为依据对受电弓参数进行敏感度评级,发现KH和MF敏感度最高。后面缩小这两个参数范围,进行单一变量匹配,寻找最优参数KH和MF。仿真结果表明接触压力波动明显减小。
4)单一变量匹配具有显著的效果,但计算得到的参数已超出范围,不具有指导受电弓实际生产的意义。接下来用50 组数据得到目标函数的多项式方程,多变量寻优得到最优参数。仿真得到接触压力的频谱图,参数优化后吊弦频率附近10~30 Hz范围内的响应的幅值明显减小。
