以真实问题构建知识联结，促进学生深度学习

何青清　曾丽丹

复习课作为数学课中的一种重要课型，主要是对新授课中的知识进行回顾梳理。如何在复习课中，激发学生的兴趣的同时，让知识之间建立联结，让复习有深度？教师可以书中内容为框架，在现实生活中寻找素材，以基础知识为点，以真实情境为线，以大问题为针，聚焦几何直观、空间观念等核心素养，通过动手操作、推理论证、图形变换等方式，发展学生的几何思维，织知识结构化的网。

一、为什么要做知识的整理与复习

小学高段数学整理与复习课是指通过学生自己动手实践、操作，对已学过的知识和技能进行系统梳理，查漏补缺，巩固已学数学知识，提高学生数学学习能力的过程。它不是对已学知识内容的简单重复，而是在学生已有的数学知识基础上对原先学习过的数学知识进行深层次的再学习。整理与复习能帮助学生梳理知识，形成知识网络，使知识系统化、结构化，进而加深对数学知识的理解和掌握，扩大数学知识之间的联系，并在此过程中弥补平时学习的薄弱环节；整理与复习更能帮助学生揭示数学规律，总结数学方法，提高综合运用数学知识分析问题、解决问题的能力，培养各种优秀的思维品质。

二、单元复习课的基本策略

（一）预设明确的教学目标，发挥目标的导向作用

小学高段数学整理与复习课教学的整体教学目标是：通过整理与复习，使学生获得的数学知识更加巩固，能运用所学的数学知识解决实际的数学问题，达到新课程标准的要求。教学中，教师首先要根据小学高段数学教材要求整理与复习的具体内容，预设每节课的整理与复习的目标。

在本堂课的预设之初，我们梳理了有关面积和体积的知识网络图，面积的教学从三年级的长方形面积计算跨度到六年级下册圆柱表面积的计算，纵向三个年级，横向两个维度：平面的面积到立体图形的表面积；有关体积的计算教学，跨度相对较小，主要集中在小学高段五六年级。归纳得出，虽然单课的知识点零散碎片化，但这部分的知识由点到线到面再到体串联形成，易于结构化整理。为了使课堂更高效的针对解决学生所出现的问题，我们对学生就图形的表面积、体积公式的计算和运用进行了前测。前测发现，学生对表面积、体积的公式应用较为熟悉，但是对表面积定义的理解出现混淆和遗忘，导致堆叠有重复面类型的立体图形表面积的计算存在一定的问题。同时对圆柱和圆锥之间的转化关系，存在一定的困难，不能将同样体积的圆柱与圆锥建立底或者高的比例关系。根据以上前期的调查，我们梳理了以下的课堂实施的教学目标：1.系统整理和练习立体图形的表面积和体积的计算方法，沟通体积计算公式之间的联系，能用相关计算方法计算有关立体图形的表面积和体积，能解决一些与表面积和体积计算相关的简单实际问题。2.经历操作、观察等数学活动，进一步体会数学知识和方法的内在联系，体会转化、类比等数学思想方法，进一步发展空间观念和推理能力。3.通过不同层次的练习，巩固计算方法，能综合运用学过的数学知识和方法解释生活中的现象，解决简单实际问题，增强解决问题的意识和反思意识。

（二）设计有效的教学活动，发挥学生的主动作用

1.营造氛围，以真实情境为点，让复习课堂变得鲜活

教师需要结合复习目标并且遵循新课程理念，对教材中的知识点进行整合，以此完善教学工作。而兴趣是推动学生学习的驱动力，同时也是学生积极主动学习的关键。基于此，教师需要先从兴趣培养入手，确保学生在复习过程中可以主动参与其中，并且主动回忆旧的知识点，将其与新的知识点进行串联。

本课以真实情景“夏天到了，最想吃的消暑食物有哪些？”为切入点，在课堂的一开始，抓住学生的兴趣点，开展本课。

2.以真实问题为抓手，促学生深度思维

在复习课时，选择符合学生生活的题材进行教学，以保证复习课程的效率。对于复习的内容而言，考虑借用生活中的数学案例，构建知识结构，保证合理性。以真实问题为抓手，由一个个点，连成线，织成网，引导学生复习，完善知识体系。

（1）以基础知识为点，扎实基础

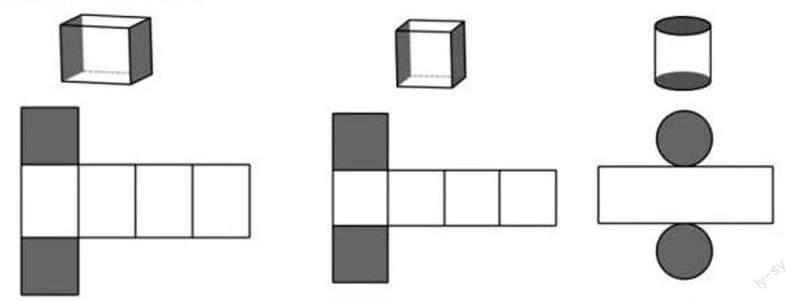
例如，教师可以让学生想一想生产不同的冰淇淋包装盒时，工厂需要考虑哪些数学方面的问题入手，引入将要研究的内容：表面积和体积（容积），接着追问：求生产冰激凌盒要多少材料，其实是求什么？什么是表面积？规则物体表面积如何计算？以问题串的形式，回顾表面积的定义、计算方法，及其运用场景。让学生猜测哪种包装盒需要的材料最多，哪种最少。教师主要考虑有以下两个层次的思维递进：一级思维：所需要的材料转化为面积类问题，二级思维：根据图形特点比较表面积。计算对于学生而言，不再是困难的点，反而如何在不计算的情况下比较大小，增加了学生的思维难度。学生需要在观察立体图形特征的基础上进行对比，学生可能会直观的发现，长方体的表面积大于正方体的表面积，而如何说明圆柱和正方体表面积的大小，学生会有一定的困难。对于正方体表面积而言，学生很快联想到S=6a2，这里需要学生打破原有的思维定式，将面拆开来进行对比，正方体、长方体都和圆柱一样，可以拆成上下两个面以及侧面，从而进行对比。

（2）以真实情境为线，深化内涵

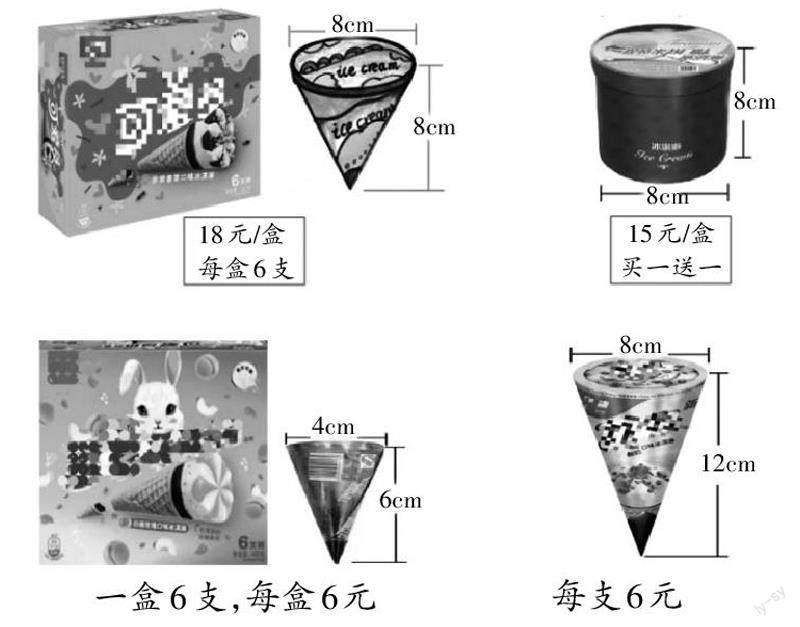
例如选购冰淇淋时如何更划算。出示超市中经常出现的场景：买赠。如下图，情况一，在真实情境中考察学生对圆锥与等底等高圆柱体之间关系的思考；情况二，同样是圆锥，半径和高均变成两倍关系，同样的价格下转换成为不同大小圆锥的体积关系。此题学生多数的做法是计算出两种圆锥的体积进行比较，而此题设计的巧妙之处在于融入比例来解决问题。半径比为R：r=2：1，那么S：s=4：1，因为H：h=2：1，所以V：v=8：1。由此创设性的将比例的知识应用至解决圆锥体积关系中来，丰富解决问题的策略的同时，打通了知识之间的联系。

几何板块的学习中，离不开空间观念的发展。空间观念主要是指：对空间物体或图形的形状、大小及位置关系的认识。空间观念的主要表现是：能够根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体；想象并表达物体的空间方位和相互之间位置关系；感知并描述图形的运动和变化规律。且2022版课标仍然突出了三维图形与二维图形的相互转化，这种转化是发展学生空间观念的重要方面。

（3）以大问题为针，织结构化的网

新课标中对数学三会中，就数学语言作为核心素养的意义中提到拓宽数学教学实践创新的视野。即以教材的设计框架为基础，在具体的内容要求和教学思路与教材保持一致的前提下，到真实生活中的数学語言里去寻找对应的情景素材。纵观整篇教学设计，用生活真实问题为线，将重合面问题、长方体、正方体、圆柱、圆锥的几何特征穿引在一起，织成了一张有关凸多面体表面积问题、体积问题相关运用与计算的网，复习课也可以有趣深刻且富有实践创新。