基于投影阈值分割和数字序列校正的高噪声数字仪表图像识别方法

郝 琨，韩 冰，李志圣*，王传启

(1.天津城建大学计算机与信息工程学院 天津 西青区 300384；2.天津凯发电气股份有限公司 天津 西青区 300384)

数字仪表在生产中发挥着重要作用，仪表读数的精准度是决定生产质量的关键因素。在工业领域，数字仪表的数据读取一般通过内置装置采集，同时配合人工定期巡检。但由于数字仪表的工作环境噪声复杂，采用人工读数易受巡检人员精力和经验影响，准确率较低，且成本较高。因此，大部分企业为了提高仪表识别准确率、节约生产成本，常采用计算机图像识别技术代替人工巡检。

1 相关工作

数字仪表的数据读取分为数字区域检测阶段和数字识别阶段，检测阶段将图像中可能包含数字的区域使用锚框标记，并将标记区域送入识别阶段进行识别。常见的数字区域检测模型有EAST[1]、TextBox[2]、DBnet[3]等。DBnet 模型使用可微二值化方法，通过网络模型训练得出图像二值化阈值，相较于其他检测模型具有较快的检测速度和较高的检测精度。因此本文使用DBnet 模型对数字区域进行检测，由于仪表数据集中数字区域和背景区域对比度较大，因此检测精度可达100%。数字识别阶段需提取图像中的数字特征并进行解码识别。传统的数字式仪表识别方法有特征检测[4]和模板匹配算法等[5]，但传统方法模板制作复杂，在识别字符种类较多情况下识别速度较慢且对于变形字符匹配效果较差，适用范围较窄， 对于噪声干扰的鲁棒性较低。

随着深度学习技术的发展，卷积递归神经网络(convolutional recurrent neural network, CRNN)[6]被广泛应用于数字式仪表的识别。文献[7]对数字仪表进行像素级的语义分割，提高了数字仪表的识别准确率，但此方法受脏污噪声影响较大，在脏污遮挡环境下易出现误识现象；文献[8]将可变形卷积应用到识别网络中，在传统卷积和池化操作中添加二维偏置值，使得神经网络可以适应不规则物体的识别，该方法提高了在少量脏污遮挡情况下的数字识别准确率，但在光线不均匀情况下该方法识别率较低；文献[9]对现有的CRNN 结构做出改进，增加注意力机制，在识别算法中使用正反两个解码器，通过结合正序和逆序两种识别结果得出读数，提高了字符粘连情况下的识别准确率，但该方法会放大图像中污渍噪声的干扰；文献[10]提出一种图像增强算法，该算法通过计算图像不同区域内的动态截断值，最终得到局部细节最优图像，解决了图像中噪声分布不均匀等问题。但该方法需要人工选定参数且会带来局部失真问题，在高曝光噪声图像上效果不佳；文献[11]使用高斯滤波平滑仪表图像，再通过自适应伽马增强算法去除复杂光线影响，解决了图像高曝光问题，但该方法无法去除密集噪点干扰；文献[12]提出一种改进的最大熵阈值分割预处理算法，能较好地去除密集噪点干扰，配合卷积神经网络，提高了高噪声环境下的仪表识别准确率，但通过该方法计算的二值化阈值偏大，在数字部分缺失情况下容易忽略特征信息；文献[13]提出一种互补序列对的运动模糊图像复原方法，利用不同图像的特征信息，使用互补帧图像修复模糊图像损失部分，但该方法使用范围较窄且无法解决多幅图像出现特征信息不足的情况。

综上，在噪声情况复杂、图像特征信息较少的情况下，数字仪表识别技术存在识别准确率较低的问题。且由于仪表图像中缺少关键特征信息, 现有的去噪声算法和神经网络优化算法对于识别准确率提升有限。因此，本文提出了结合投影阈值分割和数字序列校正的高噪声数字仪表图像识别方法PNCRNN。该方法使用投影阈值分割二值化算法(projection threshold segmentation, PTS)，将图像按噪声强度划分不同区域，并自适应设定阈值进行二值化处理，有效降低噪声干扰；接着提出数字序列校正算法(number sequence correction algorithm, NSC)，通过数字序列概率代替单个数字概率，利用前后帧图像之间的数字规律，弥补当前图像缺失的特征信息，从而提高数字图像识别准确率。实验结果表明，本文方法在高噪声环境下具有较高的识别准确率。

2 高噪声数字仪表图像识别方法PNCRNN

2.1 PN-CRNN 网络模型

目前主流的文本识别网络为CRNN。该模型包括卷积神经网络(convolutional neural networks, CNN)、循环神经网络(recurrent neural network, RNN)和时间关联性序列分类模块(connectionist temporal classification, CTC)[14]，分别对应卷积层，循环层和翻译层。CRNN 模型通过CNN 网络和RNN 网络充分提取图像特征信息并通过CTC 算法解码翻译进行对比识别，在无噪声干扰或低噪声干扰情况下识别准确率较高，但是在高噪声干扰情况下，由于数字特征信息较少，导致识别准确率较低，如图1 所示，数字“5”由于脏污遮挡影响，数字特征信息不足，CRNN 网络将其误识为“6”。

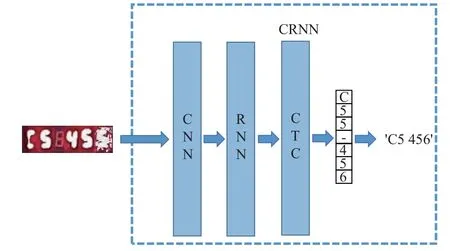
图1 高噪声情况下CRNN 识别结果

因此，为提高识别准确率，解决图像中噪声复杂以及数字特征不足导致的误识等问题，本文基于CRNN 网络提出PN-CRNN 模型。模型结构如图2 所示。PN-CRNN 首先对检测阶段得到的数字区域图像进行预处理，通过投影阈值分割算法PTS 去除图像中的噪声影响；由CRNN 网络提取图像中的特征信息，并生成预测概率矩阵；最后，利用数字序列校正算法NSC 得到精准的图像识别结果。相比于CRNN，PN-CRNN 基于数字变化规律， 利用不同仪表图像之间的相关信息，结合投影阈值分割和数字序列校正算法，有效地提高了图像特征信息利用率，解决了在高噪声环境下数字仪表识别率低的问题。

图2 PN-CRNN 模型结构

2.2 PTS 图像预处理

2.2.1 重复图像筛选

在实际的生产过程中，当图像采集设备的捕捉频率高于仪表读数变换频率时，会出现图像重复采集情况，导致识别过程时间损耗增加，因此本文通过对比图像中关键区域的像素密度进行重复图像筛选。

由于数字部分在图像中占较大比例且与背景有较大对比度，因此图像中的关键区域可认为是数字区域。本文通过垂直投影法对数字区域进行划分。将图像中数字边界像素值设为阈值进行垂直投影，选取投影图中波谷坐标作为划分边界将图像划分为不同数字区域。在无噪声情况下，图3 所示图片可划分出5 个数字区域；当图像噪声较大时，数字出现粘连现象，导致投影图中波谷相互连接，此时将连接区域作为整体处理，则图片可划分出3 个数字区域，如图4 所示。

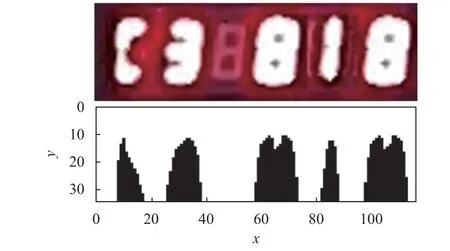
图3 垂直投影图

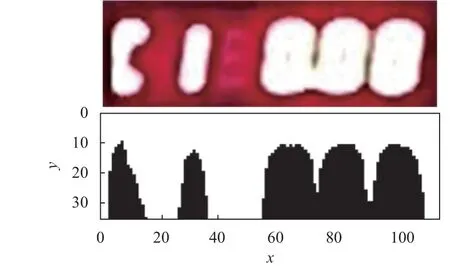
图4 高噪声情况下垂直投影图

设数字边界像素值为C0，数字区域中灰度级i的 像素个数为mi，灰度范围为 [C0,255]，则区域内总像素数为：

数字区域像素点密度为：

式中，l和h别表示数字区域的长度和高度。当两幅图像中数字区域个数相同且对应数字区域内像素点密度相似时，则判断为重复图像。

2.2.2 投影阈值分割算法

由于数字仪表工作环境复杂，噪声影响较大，常见的图像增强算法和图像二值化算法均不能完全满足实际生产需求[15]。因此本文结合全局阈值分割和局部阈值分割优点，根据图像数字区域内噪声强度大小自适应设定二值化阈值。通过实验验证，本文提出的投影阈值分割算法效果优于常见的图像增强算法和二值化算法。

数字区域内二值化阈值表示为：

式中，p和p¯分别表示该数字区域像素点密度和无噪声情况下数字区域平均像素点密度。

图像二值化操作后需要通过形态学算法去除剩余噪声，当图像受到水滴、雾气等噪声影响，容易发生图像特征丢失现象，如图5a 所示。此时使用腐蚀等算法会造成部分特征丢失，受噪声影响的数字区域经二值化处理后出现断裂现象，数字被分成多个连通区域，如图5b 所示。因此需要对二值化处理后的图像进行修补。

图5 数字修补对比图

本文提出的修补方法是以数字“1”的横向宽度作为修补标准，对数字区域内像素点进行筛选。当以该像素点为中心的矩形区域内纵向像素点数量过少时，则认为是噪声点或是边界点，不做处理；若竖向像素点形成连通区域且横向像素点数量小于标准值则进行修补。

修补过程将图像中断裂数字进行补全，多个特征信息融合为所需特征信息。如图5c 所示，数字‘7’经修补后仅存在一个连通区域，且数字特征十分明显，避免了特征信息不足导致的误识问题。

2.3 NSC 数字序列校正算法

2.3.1 NSC 算法概念

实际生产中，大部分仪表的读数是基于一定规律变化的，如水表、电表。水表的读数表示用水量，数字按规律逐渐变大，如“1，2，3”或“1，3，5”。因此当规律变化的数字中有无法识别的情况，可以借助数字变化规律进行推测，如图6 所示，已知前两帧图像中最后一位数字分别为“3”和“4”，第三帧图像中最后一位数字受到噪声影响无法识别，但依照前两帧图像数字变化规律，该数字有较大的概率为“5”。

图6 数字变化规律图

NSC 算法基于数字规律变化的前提，将单个数字的识别变为对包含该数字的数字序列识别。原始的CRNN 模型选择识别概率最大的字符作为识别结果，当遇到高噪声导致的图像特征信息不足情况，会产生误识的情况。NSC 算法选择识别概率最大的数字序列作为序列识别结果，数字序列的识别概率由组成该数列的多个数字识别概率相乘所得，因此识别准确率受数字序列整体影响，降低了噪声对单个数字识别准确率的干扰权重。

2.3.2 NSC 算法流程

假设数字跳动间隔为k，数字序列长度为n，上限为N。 STR1,STR2,···,STRm用于存放可行数字序列，m表 示可行数字序列的数量。设P1,P2,···,Pm为可行数字序列概率。Pout表 示输出概率，Pidx表示输出的数字序列。则NSC 算法流程如图7 所示。

图7 NSC 算法流程图

1)设定数字跳动间隔k和数字序列长度上限N，计算可行数字序列数量m和可行数字序列，并将可行数字序列存放在S TR1,STR2,···,STRm中；

2)对数字序列概率P1,P2,···,Pm和 序列长度n赋初值，令P1=1，P2=1,2,···，Pm=1，n=1；

3)判断数字序列长度n是否大于上限N，如果不是，转入步骤4)，如果是，转入步骤5)；

4)获取识别网络对数字“0～9”的识别概率P1,P2,···,P9， 计算数字序列概率，序列长度n=n+1,转入步骤3)；

5)输出最大识别概率Pout和对应的数字序列Pidx作为识别结果，流程结束。

2.3.3 NSC 算法有效性证明

为说明NSC 算法的原理和有效性，本文做如下数学证明。

将图片中某个位置数字的真实值记为i，识别为正确数字i的概率记为pi,i， 识别为错误数字i′的概率记为pi,i′， 其中i,i′∈[0,9]，i≠i′。假设该位置数字的跳动间隔为1，将该位置上长度为n的数字序列 记 为S[i][i+1][i+2]···[i+j]···[i+(n-1)]， 其 中i+j为(i+j)mod10 的 简记，下文中的i+j、i+j+k等均为简记。数字序列的概率为组成序列中数字的概率乘积，假设数字序列的初始数字为i，序列长度为n，识别为正确数字序列的概率记为：

识别为错误数字序列的概率记为：

经观察发现，存在以下启发规则。

在高噪声条件下，识别为正确数字的概率pi,i会发生下降，但从整体数据分析，识别为正确数字平均概率仍大于识别为错误数字的平均概率。

数字概率分析实验说明了该启发规则的正确性。

已知数字序列中，单个数字的识别概率分布相互独立[16]，假设识别为正确数字的概率服从以μ¯correct为均值的分布；识别为错误数字的概率服从以 μ¯wrong为均值的分布[17]。由启发规则和假设条件提出如下命题：

证明：正确数字序列概率乘积的期望ES(Pcorrect)和错误数字序列概率乘积的期望ES(Pwrong)分别为：

则可得：

由命题1 可知在数字序列长度n达 到一定程度时，正确数字序列依概率大于错误数字序列，算法的有效性得到保证。在实际测试中，当数字序列长度达到8 时，PN-CRNN 模型识别准确率趋于稳定。

2.3.4 NSC 算法的影响因素

2.3.4.1 数字序列长度

2.3.4.2 可行数字序列数量

数字序列有多种可能，将满足已知规律的数字序列定义为可行数字序列，其余为干扰数字序列。

在固定数字序列长度n的 前提下，NSC 算法受到可行数字序列数量的影响。可行数字序列数量决定算法的时间复杂度，当可行数字序列数量过于庞大时，算法难以满足实时识别。

可行数字序列数量受数字跳动间隔影响，数字跳动间隔可认为是数字序列的规律。如数字跳动间隔取值为1 时，数字序列“1, 2, 3”为可行数字序列，数字序列“1, 5, 8”为干扰数字序列。当数字跳动间隔未知时，数字序列没有规律约束，所有数字序列都是可行数字序列。

2.3.5 NSC 算法参数的优化

2.3.5.1 重复图像筛选

重复图像会极大增加可行数字序列的数量。以数字i∈[0,9]， 序列长度n为例，此时可行数字序列共有1 0n种可能，如图8a 所示。通过PTS 预处理算法剔除重复图像后，可行数字序列数量降低为10×9n-1种可能，如图8b 所示。

图8 可行数字序列数量

2.3.5.2 数字跳动间隔约束

在实际生产中，由于仪表数字变化情况不固定，因此数字跳动间隔取值情况存在多种可能。

假设数字i∈[0,9]， 数字序列长度为n， 当数字跳动间隔有两种取值时，以1, 2 混合情况为例，如图9a 所示，可行数字序列数量为1 0×2n-1种；当数字跳动间隔有3 种取值时，以1, 2, 3 混合情况为例，如图9b 所示，可行数字序列数量为10×3n-1种。由此可得，可行数字序列数量随数字跳动间隔的取值数量增大而增大，因此减少数字跳动间隔的取值数量可以有效减少可行数字序列数量。

图9 控制数字跳动间隔优化

数字跳动间隔在影响可行数字序列数量的同时也影响了NSC 算法的准确率。假设数字仪表规律变化，数字跳动间隔为1 所得数字序列如图10a 所示，数字跳动间隔为2 所得数字序列如图10b 所示，数字跳动间隔由1 加大为2 时，数字序列的长度对应由10 减少为5。当数字跳动间隔过大时，数字之间呈现无序跳动，导致NSC 算法失效。因此减小数字跳动间隔取值大小可以有效增加NSC算法的识别准确率。

图10 跳动间隔对数字序列影响

实际生产中，数字跳动间隔可通过改变采集设备的图像采集频率约束，当仪表图像变化规律时，加快采集频率可以减小数字跳动间隔取值数量和取值大小。

3 实验与结果分析

3.1 数据集

本文采用的数据集1 由电力企业通过监控摄像对仪表设备进行实时采集制成，共3 510 张。为了验证NSC 算法在高噪声情况下的效果，本文在高噪声环境下对仪表设备进行采集，得到噪声图像500 张；同时在数据集1 中随机抽取部分图像并通过数据增强方法添加噪声，得到噪声图像404 张，将其与采集所得噪声图像混合，制作了高噪声情况下的数据集2，共904 张，如图11 所示，其中包括仪表镜头被脏污遮挡、光线过强导致的过曝、仪表电子元件损坏导致数字显示不完整等情况。数据集共有4 414 张图片，2 822 张用于网络训练，1 592 张用于测试。

图11 不同图像噪声

3.2 实验平台

本文实验使用计算机硬件设备为Intel(R)Core(TM) i7-7800X CPU@3.50 GHz，模型训练使用2 个显存为11 GB 的GeForce GTX 1080Ti 上训练。计算机系统为Ubuntu18.04LTS。

3.3 评价指标

本文采用准确率(accuracy, Acc)和每秒传输帧数(frames per second, FPS)作为评价指标。correct_num是正确的识别图像数量， all_num是图像总数，准确率计算公式为：

3.4 结果分析

3.4.1 PTS 算法实验结果分析

预处理算法主要用于去除图像噪声，在保留特征信息的同时减少噪声影响。图像的预处理方法分为非物理模型的增强方法和基于物理模型的复原方法。

常用的增强方法有带色彩恢复的多尺度视网膜增强算法(multi-scale retinex with color restoration,MSRCR)[19]，自动彩色均衡算法(automatic color equalization, ACE)[20]，限制对比度自适应直方图均衡算法(contrast limited adaptive histogram equalization,CLAHE)[21]。

除图像增强算法之外，图像二值化处理也是常用的降噪方法[22]。常见的图像二值化算法有平均灰度阈值分割和自适应的最大类间方差法(maximum inter class variance, OTSU)[23]。

本文选择ACE 算法、MSRCR 算法、CLAHE算法、OTSU 算法、全局阈值分割算法以及PTS算法进行对比实验。

图像增强算法可以增强图像中前景和背景的对比度，改善过曝情况，但同时会提高噪声影响。如图12a～图12d 所示，图像增强算法无法去除图像密集噪点。

图12 预处理算法对比

全局阈值二值化分割时间复杂度较低，通过选取图像中字体区域的平均像素值作为阈值对图像进行简单的分割。阈值选取影响二值化图像的质量，阈值过大会导致图像丢失部分特征，阈值过小则无法去除噪声干扰，如图12e 所示。自适应的阈值分割算法，通过自适应选取阈值对图像进行分割，当图片中前景和背景对比度较大时，Otsu 算法计算所得阈值偏小，去噪效果较差，如图12f 所示。PTS 算法通过垂直方向投影将图像划分为不同区域，针对区域内噪声强度自适应选取分割阈值，并使用形态学方法减少噪声干扰。相比于全局阈值分割算法和Otsu 算法有更好的去噪效果，如图12g所示。

预处理算法对比实验使用CRNN 模型，主干网络采用MobileNetV3(slim)，首先在低噪声数据集1 上测试噪声干扰较小情况下预处理算法效果。实验结果如表1 所示。从表1 中可以看出，图像增强算法对识别率提升效果有限；全局阈值分割算法损失了图像部分特征，导致识别准确率下降；Otsu算法对噪声比较敏感，相比于原图识别准确率下降约14%；PTS 算法使用二值化处理消除部分噪声，并通过投影分割方法解决阈值选取过高造成特征信息丢失的问题，相比于原图识别准确率提高约1.3%，相比全局阈值算法识别准确率提高约2.7%。

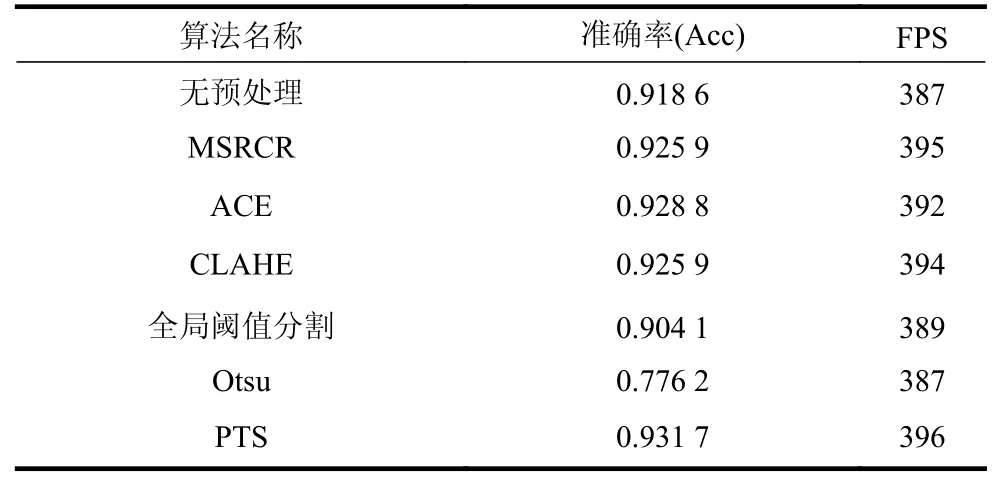
表1 在数据集1 上的预处理算法对比

通过在低噪声数据集1 上的预处理对比实验可知，图像增强算法提升效果有限，且相比于图像二值化算法，图像增强算法复杂度较高[24]。为进一步对比几种预处理算法的效果，使用高噪声数据集2 进行测试，实验结果如表2 所示，使用PTS 算法处理后，图像识别准确率对比原图提高约15%，对比使用全局阈值分割算法高约10%，对比使用图像增强算法提高约6%。实验结果表明，PTS 算法对比其他算法，有更强的去噪效果。

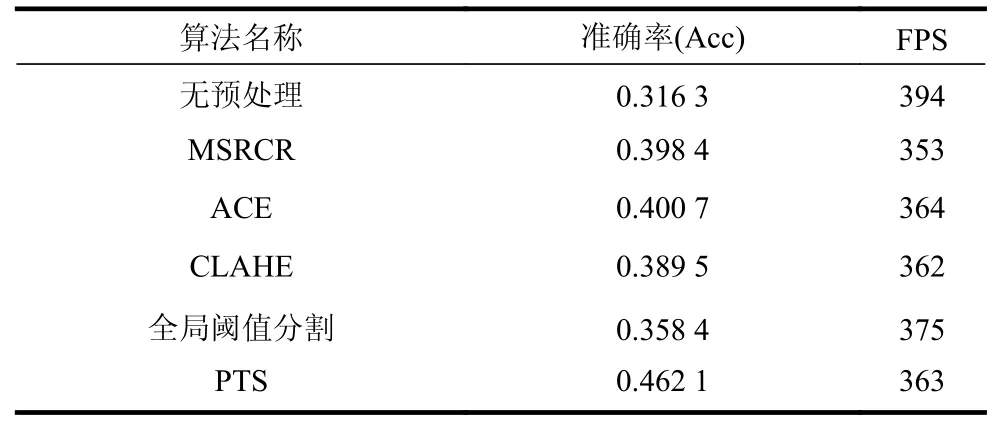
表2 在高噪声数据集2 上的预处理算法对比

3.4.2 数字序列概率分析

为验证NSC 算法启发规则 μ¯correct＞μ¯wrong的正确性，使用低噪声数据集1 和高噪声数据集2 进行实验。

高噪声数据集2 分析结果见表3，正确数字平均识别率为0.475，错误数字平均识别率为0.057，错误数字平均识别率小于正确数字平均识别率。低噪声数据集1 分析结果见表4，正确数字平均识别率为0.962，错误数字平均识别率为0.014，错误数字平均识别率远小于正确数字平均识别率。

表3 在高噪声数据集2 上的数字平均识别率乘积

表4 在数据集1 上的数字平均识别率乘积

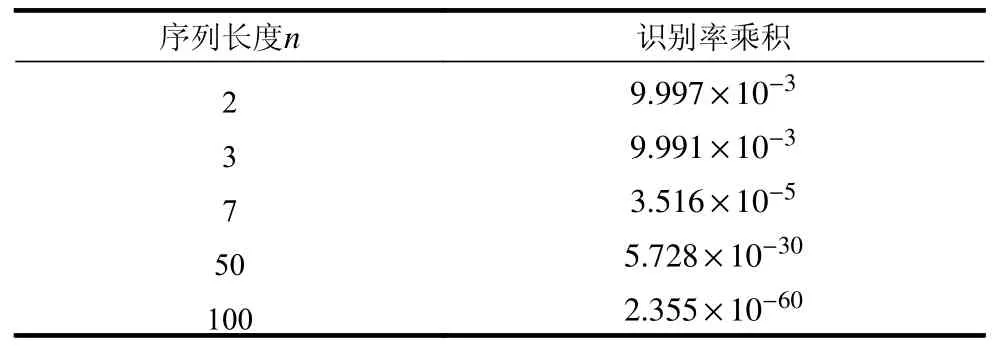
表5 在高噪声数据集2 上的正确识别率乘积

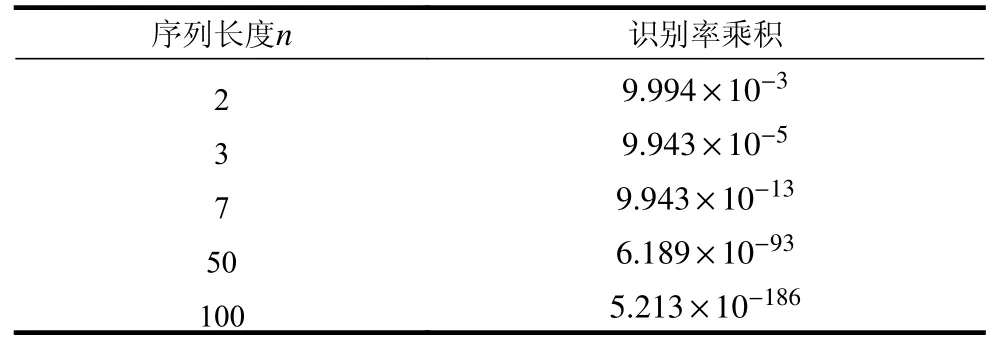
表6 在高噪声数据集2 上的错误识别率乘积

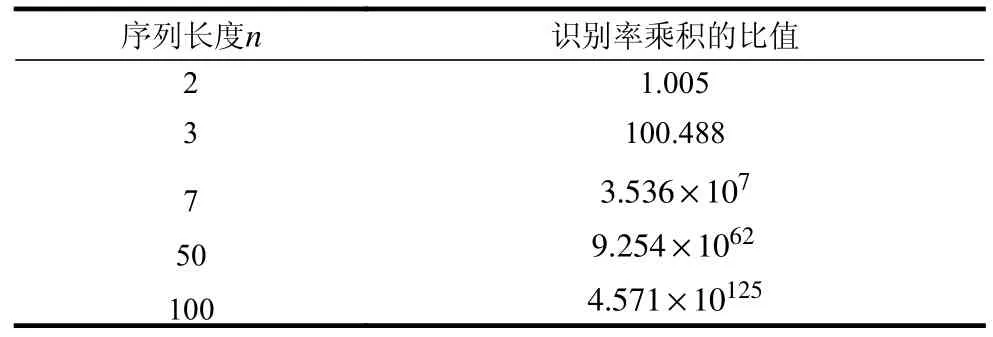
表7 在高噪声数据集2 上的正确识别率与最大错误识别率乘积比值

从两组实验数据对比可知，NSC 算法的启发规则成立。

3.4.3 NSC 算法效果测试

为验证NSC 算法的效果，使用高噪声数据集2 测试。原始CRNN 模型选用PaddlePaddle 平台数字识别模型[25]，并对其添加PTS 算法和NSC 算法。如表8 所示，仅使用NSC 算法相比于原模型识别准确率提高约37%，同时使用PTS 算法和NSC 算法相比于原模型提高约62%。

表8 在高噪声数据集2 上的NSC 算法效果

3.4.4 数字序列长度对NSC 算法影响

NSC 算法的序列长度由参与运算的数字个数决定，序列长度为1 的情况即原始模型。当序列长度增大时，模型识别准确率逐渐增大，如表9 所示，因此NSC 算法效果随数字序列长度n增加而增强。随序列长度增大，识别准确率上升趋势逐渐变缓，如图13 所示。在实际测试中，当序列长度增大到某一阈值，识别准确率达到最大值并不再增长。

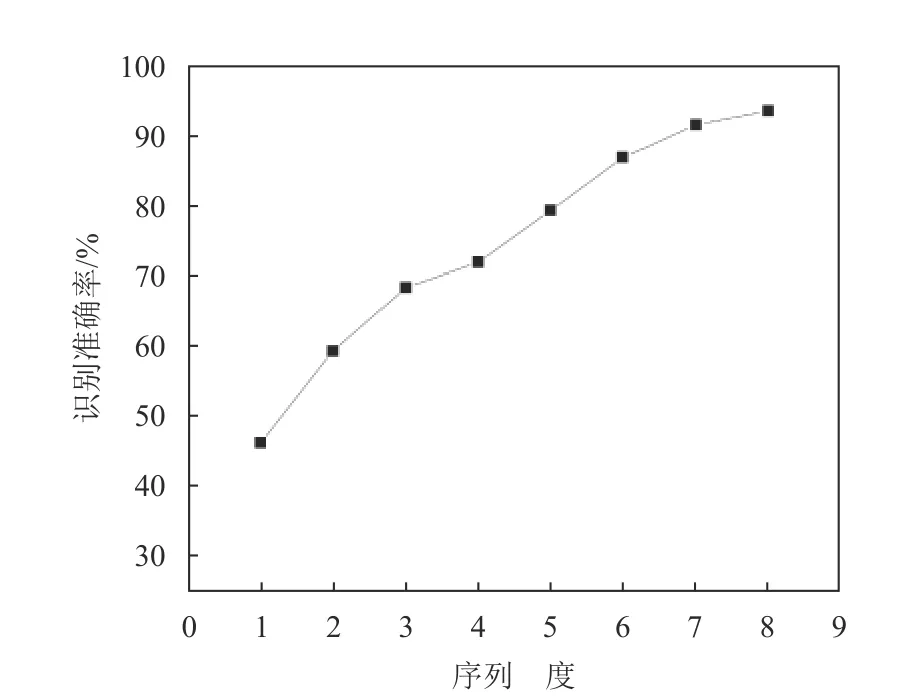
图13 序列长度与识别准确率关系

3.4.5 数字跳动间隔对NSC 算法的影响

NSC 算法受到数字序列数量影响，数字序列数量由数字跳动间隔和起始位置决定。数字跳动间隔由1 增加到2 时，如表10 所示，准确率下降约5%；当改变起始位置时，数字跳动间隔变为1 和2 混合情况，准确率下降约9%。同时改变数字跳动间隔和起始位置，准确率下降约12%。由实验结果可知，数字的跳动间隔是影响算法识别准确率的重要因素。在实际测试中，算法使用的序列长度较短，当数字跳动间隔过大时，数字无法形成序列。针对此问题可通过调校设备采集时间间隔，增加采样次数，避免数字无序跳动，保证算法效果。

表10 数字间隔对NSC 算法影响

3.4.6 模型对比实验

在数据集1 上，对比PN-CRNN 模型与CRNN模型在正常情况下识别准确率，主干网络选择MobileNetEnhance、 MobileNetV3[26]， ResNet[27]和MobileNetV3(slim)。如表11 所示，添加PTS 算法和NSC 算法后模型准确率均有不同程度的提高，其中MobileNetV3(slim)的识别准确率可达到96.32%。

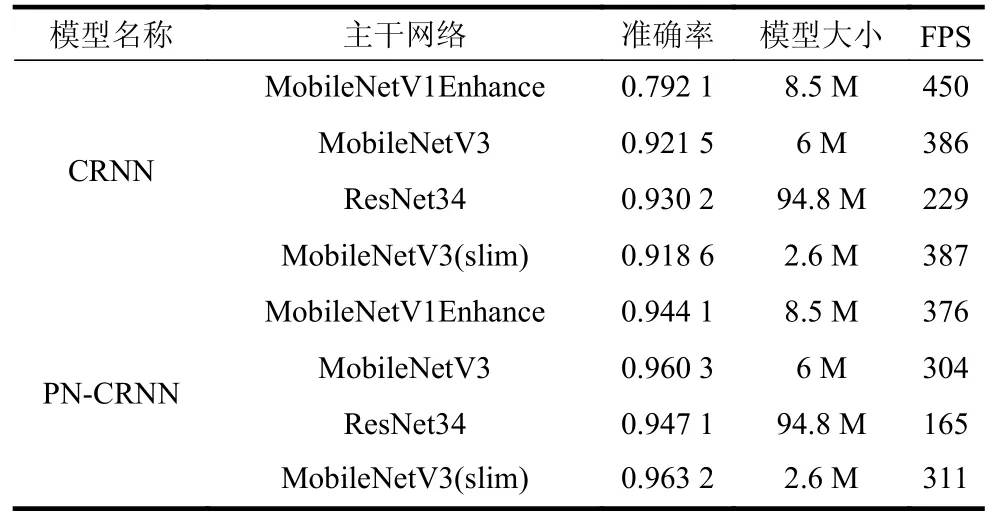
表11 在数据集1 上的模型对比

为进一步验证模型效果，本文选择基于SVTR[28]和PP-LCNet[29]的PP-OCRv3 模型进行对比实验。如表12 所示，PN-CRNN 模型相比于PP-OCRv3模型在数据集1 上准确率提高约2%，在高噪声数据集2 上提高约22%。

表12 PN-CRNN 与PP-OCRv3 模型对比

4 结 束 语

本文针对仪表图像噪声复杂问题，提出了一种基于投影阈值分割和数字序列校正的高噪数字仪表图像识别方法。首先使用PTS 投影阈值分割算法去除仪表图像噪声，以便于模型提取数字特征。然后通过NSC 数字序列校正算法将单个数字概率转变为数字序列概率，避免了因数字特征信息不足导致的误识、漏识问题。实验结果表明，在高噪声数据集上，本文算法对数字的识别准确率达到93.64%，远远高于其他算法，具有很好的实用性。然而，本文算法存在对于数字序列条件要求较高、忽略了图像中数位之间存在的规律等不足，未来将会针对这些不足继续开展后续研究工作。