巧用振幅矢量法求解简谐运动的时间
2023-10-14刘钦钊马仕彪
陈 龙 刘钦钊 马仕彪
(安徽省濉溪中学,安徽 淮北 235100)
在高中物理中,能精确求解时间的运动过程并不多,常见的是匀速直线运动和匀变速直线运动。对于变加速直线运动偶尔也可以通过特殊方法求解,比如在机车启动过程中可以利用牵引力做功等于恒定功率乘以时间来求解,在电磁感应现象中可以利用动量定理来求解。对于变加速运动求时间的问题,原则上都可以利用微积分求解,这种方法对学生的数学要求较高。如果利用简谐运动的知识,很多变加速过程的时间问题都可以相对容易地得到解决,而不必借助微积分。
但是对于简谐运动,高中阶段也大多考查与周期等相关时间的求解,如果将简谐运动与旋转矢量相结合,简谐运动中任意过程的时间都可以求解。
1 简谐运动和振幅矢量法
物体在平衡位置附近的往复运动称为振动。从力的角度来说,物体之所以在平衡位置附近做往复运动,是因为它离开平衡位置后会受到一个指向平衡位置的力,这个力称为回复力。如果回复力的大小与物体相对平衡位置的位移成正比,且始终指向平衡位置,用公式表达为:f=-kx,其中负号表示回复力和位移的方向相反,k为比例系数,这种回复力称为线性回复力,此时物体的振动为简谐运动。
如图1所示,水平放置的轻弹簧一端固定,另一端与滑块相连,置于光滑水平面上,弹簧无形变时物块处于O点,将其移动至a点由静止释放,滑块开始做变加速运动,从a点开始通过O点到达a′点,然后又经过O点回到a点,此后重复上述运动过程。a点和a′点到O点的距离相等,这个距离称为简谐运动的振幅,记为A,它对应物体离开平衡位置的最大位移。从a→O→a′→O→a,这个往复过程具有周期性,周期为T。物块在位移x处,弹簧弹力与位移的关系为:f=-kx,其中k代表弹簧的劲度系数,负号代表弹簧弹力与位移方向相反,可见弹簧振子满足做简谐运动的条件。
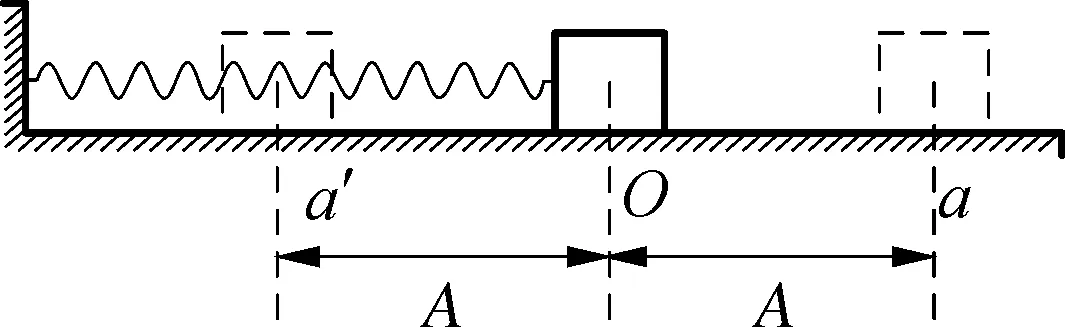
图1

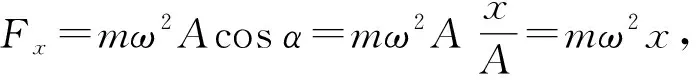

图2

旋转矢量的角速度对应简谐运动的角频率,旋转矢量在计时开始时与x轴的夹角对应于简谐运动的初相位,旋转矢量的长度对应于简谐运动的振幅。因此任意一个简谐运动都与一个上述的旋转矢量相对应,简谐运动的任意一个位置都与旋转矢量圆上的点相对应,这种处理简谐运动的方法叫作振幅矢量法。如图3所示,在物体做简谐运动的过程中,经过的点分别与圆上的点对应。利用这种方法可以很直观地描述简谐运动,便于解决问题,特别是当问题所对应的简谐运动过程不是四分之一周期的整数倍时,时间的求解就会变得非常直观、简单。
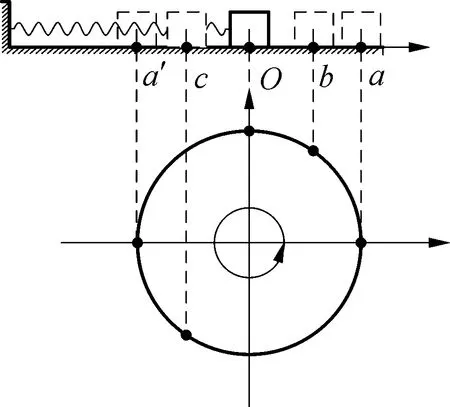
图3
2 振幅矢量法的应用
例1:物体从倾角为θ的斜面顶端由静止开始下滑,动摩擦因数从顶端到底端按照μ=kx变化,且物体未到达底部前已停止运动,求物体从开始到停止运动所经历的时间。


图4
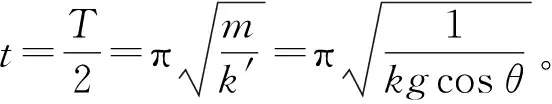
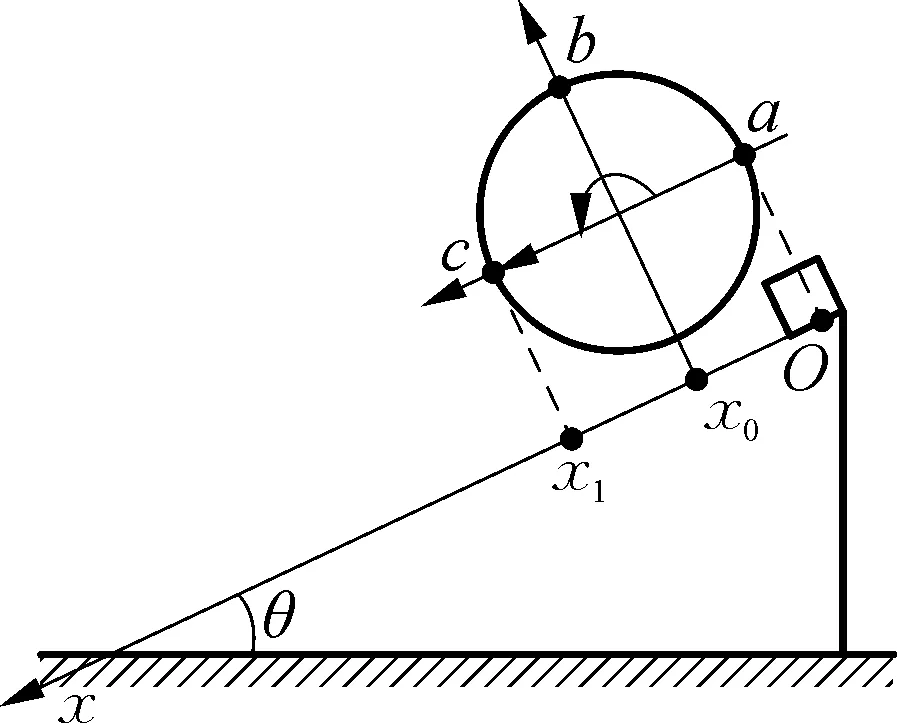
图5

例2:劲度系数为k的轻弹簧竖直固定在水平桌面上,将小球放于弹簧上端,静止时弹簧的压缩量为x1。按压小球使弹簧继续被压缩,压缩的距离为x2,且x2>x1然后松开,求小球上升到最高点所需时间。
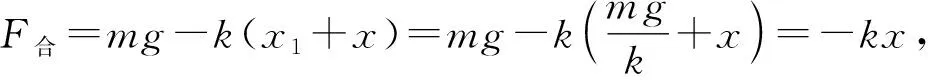

图6
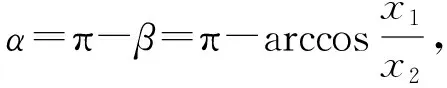
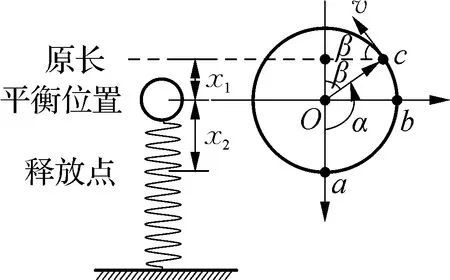
图7
点评:小球和弹簧构成了竖直方向的弹簧振子,小球做简谐运动。但是从小球开始运动到脱离弹簧,整个过程大于四分之一周期而又小于半个周期,无法用常规的方法求解时间。利用旋转矢量圆,时间的求解就转化为旋转矢量转动角度的求解。
例3:轻弹簧劲度系数为k,一端固定在墙壁,另一端连接质量为m的物块,物块与桌面间的滑动摩擦力为f。开始时弹簧处于自然长度,物块的初速度为v0,从开始压缩弹簧到速度为零用时为t1,接着从速度为零到再次恢复原长用时为t2,求t1和t2。
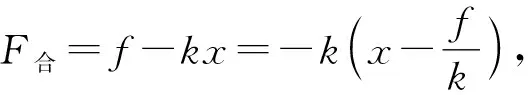

图8


图9
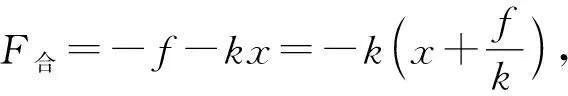

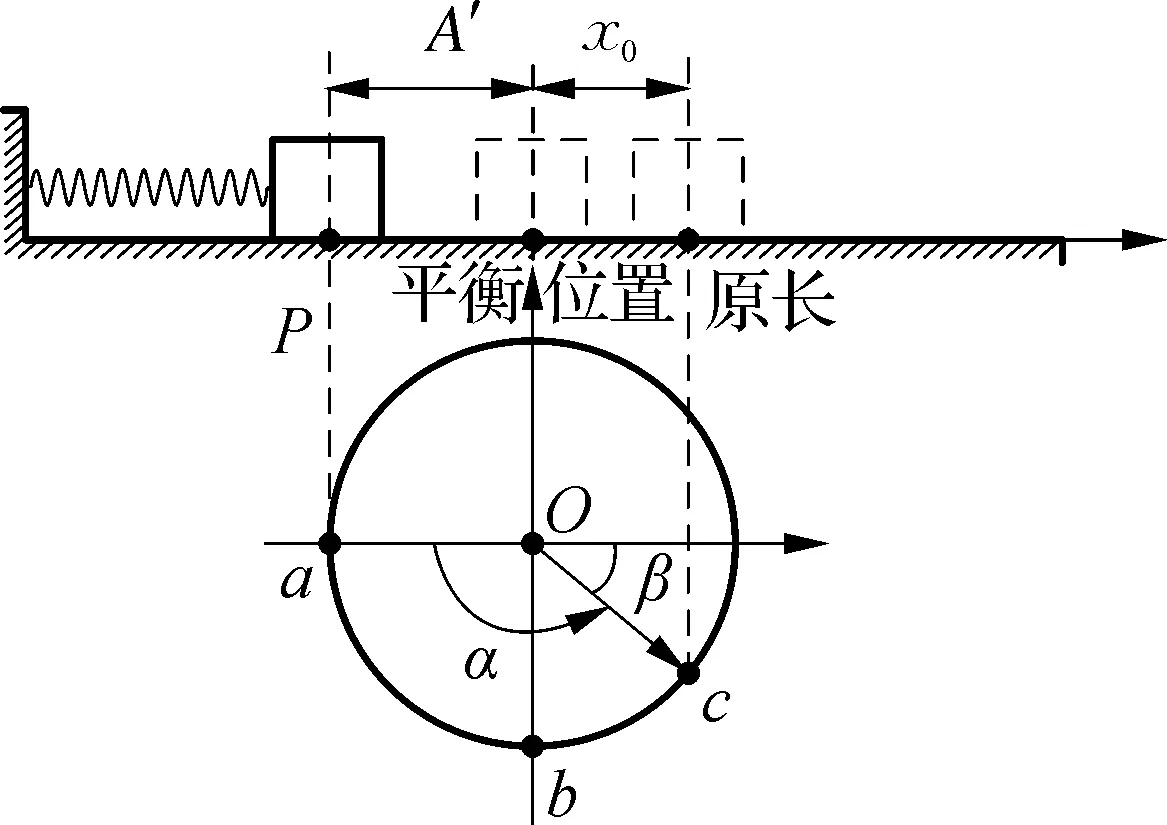
图10
点评:相比于例2,例3中物块的平衡位置在改变,这是因为物块在左、右运动时所受滑动摩擦力的方向发生了变化,所以本题的关键是确定好这两个不同的平衡位置,以及由于不同的平衡位置所导致的不同振幅。
综上所述,只要我们能够确定物体的运动是简谐运动,结合振幅矢量法,很多常规方法很难处理的时间、速度等问题都可以轻松求解。
