航空发动机复合材料声衬声学模型构建及吸声性能仿真
2023-10-13杨智勇蒋文革左小彪耿东兵朱中正
杨智勇, 侯 鹏, 蒋文革, 杨 磊, 左小彪,耿东兵, 朱中正, 李 华*
(1.航天材料及工艺研究所,北京 100076;2.沈阳发动机研究所,沈阳 110015;3.上海交通大学 材料科学与工程学院,上海 200240)
随着全球范围内民用航空业的快速发展,飞机噪声问题越来越受到重视,飞机的噪声标准也日趋严格[1-2]。大型飞机的噪声源主要可以分为两大类:发动机噪声和机体空气动力噪声。在发动机噪声控制中,使用管道声衬技术对噪声进行吸收是一种常见而有效的降噪手段[3-4]。
声衬主要可以分为单自由度声衬(single-degree of freedom,SDOF)和双自由度声衬(double-degree of freedom,DDOF)[5]。典型的SDOF 声衬主要由面板、蜂窝芯以及刚性背板构成。面板常有开孔板、铁丝网或开孔夹层板,蜂窝芯连接在面板后构成了芯腔,与窝芯连接的刚性背板使芯腔密封且相互之间隔离,多个密封芯腔结构形成一种排列整齐的并联亥姆霍兹共振器,为共振吸声结构[6-10]。DDOF声衬是在SDOF 声衬的基础上再添加一层吸声材料和穿孔板,原来的穿孔板配合金属丝网和吸声膜变为中间层,从而变成双层结构。这样使得吸声频段变得更宽,吸声特性增强,可针对不同的频率区段内的噪声设计出合理而适用的声衬[11-12]。
航空发动机声衬的声学设计是降低航空噪声的重要手段之一,目前声学设计方法主要分为两类:一类是解析方法,例如模态匹配方法[13]、边界元方法[14]和传递单元法[15]等,解析方法计算效率高,但应用范围有限,只能对简单规则结构进行计算:另一类是数值方法,包括有限元方法[16]和计算气动声学(CAA)[17]等,其中有限元方法是发展较为成熟的一种,该方法适用性强,计算快速,方便优化设计,能够尽可能准确地检验结果,适合工程应用。
声衬工作频率是由其结构决定,只对特定频率的噪声敏感,在超出该范围后的吸声效果迅速下降,当声波进入小孔后便激发空腔内空气振动,如果声波频率与该结构共振频率相同时,腔内空气便发生共振,穿孔板孔颈处空气柱往复振动,速度、幅值达最大值,摩擦与阻尼也最大,此时,使声能转变为热能最多,即消耗声能最多,从而发挥高效吸声作用[18-20]。因此,其吸声特性呈现峰值吸声的现象,即在某一个频率达到最大,在离开这个频率附近的吸声系数逐渐降低,在共振区间内吸声效果较为明显,但是在远离共振频率处几乎无效果。当声衬结构参数确定后,敏感频率随之确定[21-22]。
本工作通过仿真计算,研究复合材料单自由度声衬与双自由度声衬的消音板孔直径、孔间距、蜂窝高度和消音板厚度对吸声性能的影响,并对比不同自由度声衬的降噪差异。
1 仿真技术设计与复合材料构件降噪实验设计
1.1 技术路线
本研究计算模型如图1 所示,仿真时采用二维轴对称模型,考虑到声波管道传播特点,管道模态声源需要定义在等截面管道边界,将入口端等截面延伸一段(200 mm)用于后续声源的定义。
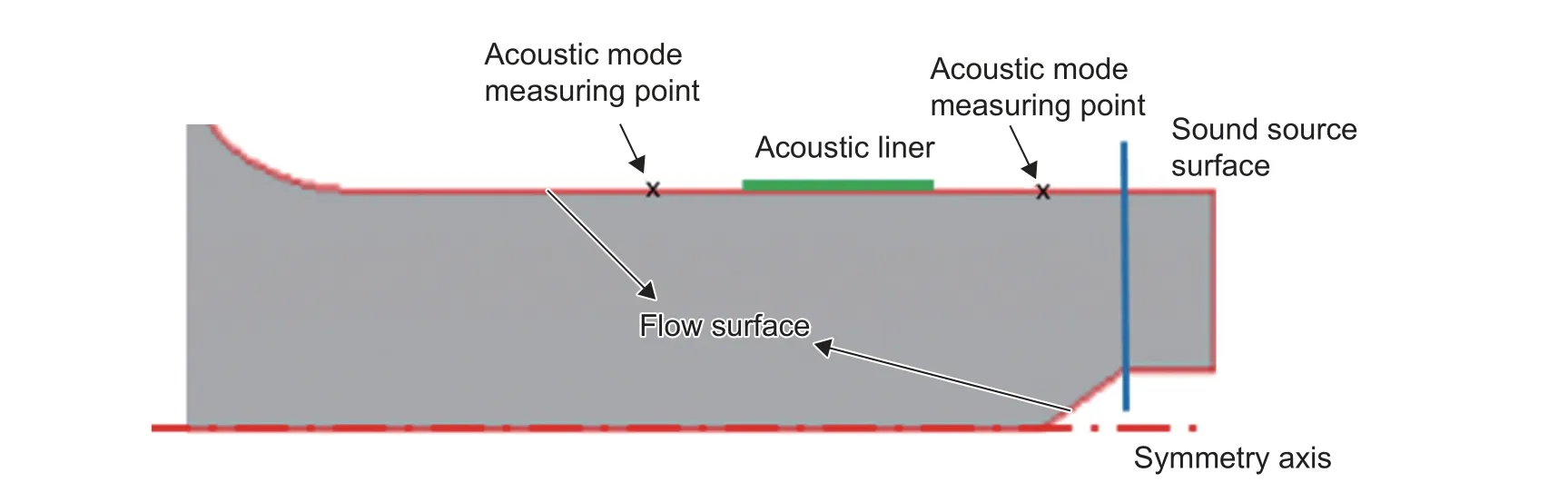
图1 有流计算模型示意图Fig.1 Schematic diagram of calculation model with flow
技术路线如图2 所示,由于声源面进行了延伸,延伸后截面的流速、密度和声速等均未知,因此需要进行背景流场(computational fluid dynamics,CFD)计算,通过流场计算提取延伸后的声源面声速、密度和流速等参数在后续Actran 背景流场计算和声传播计算中作为边界输入。CFD 计算在Fluent 中完成,声学计算在Actran 中完成。
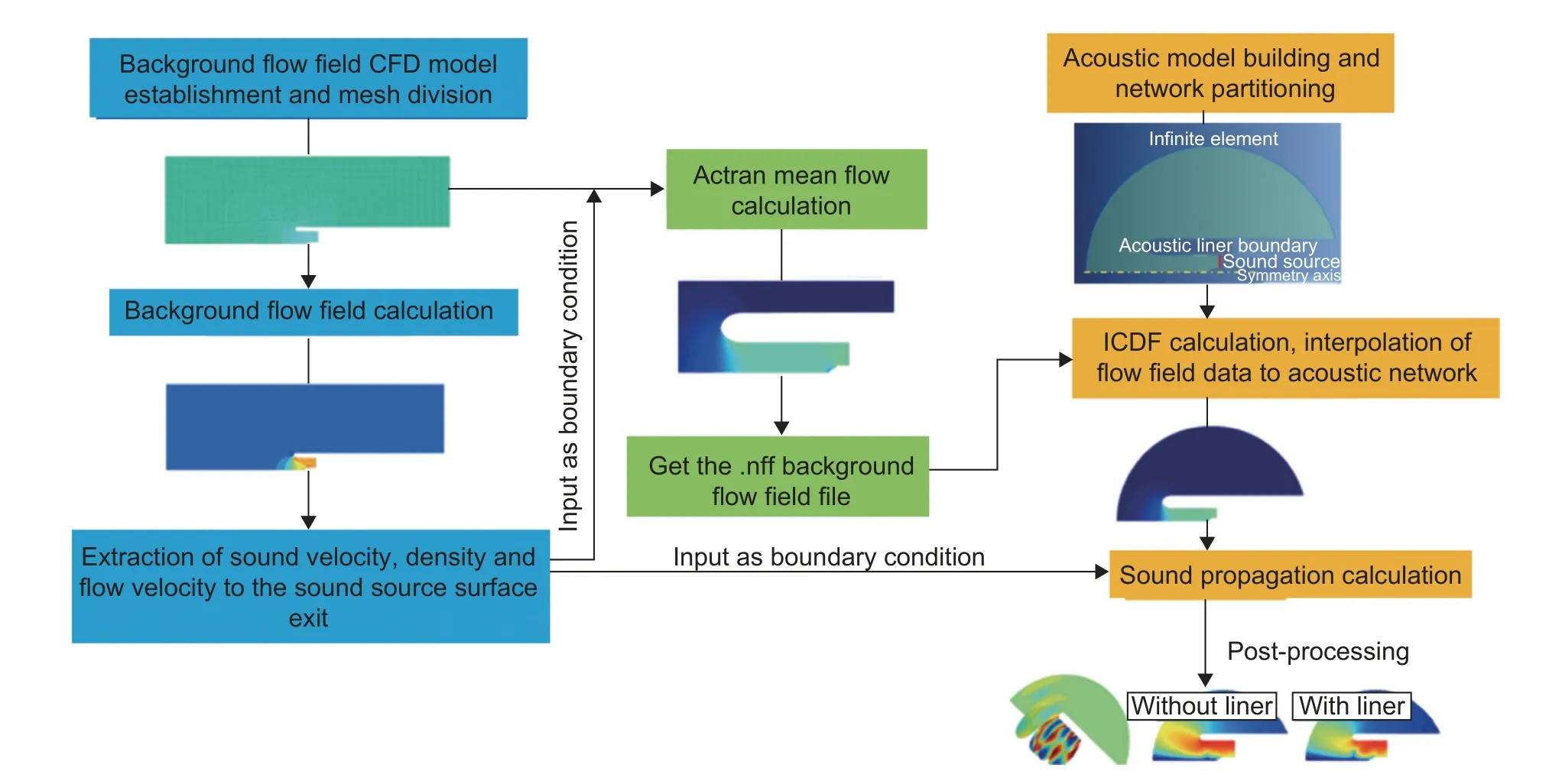
图2 仿真技术路线Fig.2 Simulation technology approach
1.2 计算工况说明
试件共有3 个流场工况,主要考察不同流场状态、不同声模态激励下叶片通过频率(blade passing frequency, BPF),即BPF 和2BPF 处的声学响应,详细流场状态参数如表1 所示。

表1 试件状态流场参数Table 1 State flow field parameters of test pieces
1.3 测试原理
图3 为实验测试系统,实验台分为声源段、待测段和末端排放段。声源段提供声源激励,待测段放置声衬试件,在声衬试件进口端和出口布置传声器,获得声衬进、出口端声学结果,从而得到声衬的传递损失TL。末端排放段连接消音室,消音室布置传声器,测试系统声辐射,通过对比有无声衬该处的声压级(声功率级)可以得到系统的插入损失IL。无发动机样机测试时,声源段可以在外部增加声源激励,同时通过增加气源制造背景流,测试不同流场状态下声衬的降噪效果。
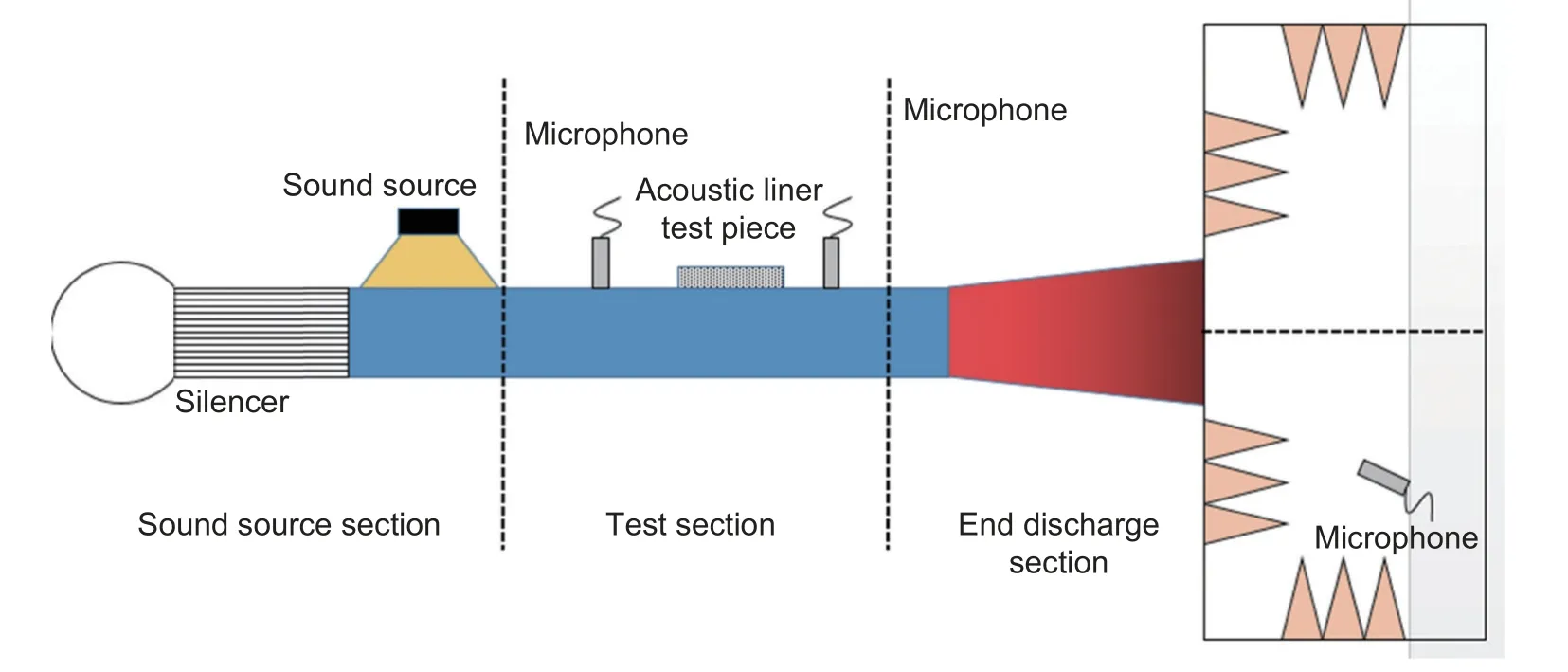
图3 实验台示意图Fig.3 Schematic diagram of test bench
插入损失IL为系统中安装声衬前后在系统外某定点测得的声功率级(声压级)
式中:Lw1为安装声衬前某测点的声压级,dB;Lw2为安装声衬后某测点的声压级,dB;W1为安装声衬前某测点的声功率;W2为安装声衬后某测点的声功率。
1.4 测试工况与样件
(1)流速:M=0.35 Ma;
(2)声压级:选取SPL=110、120、130、140、150 dB 五个声压级;
(3)频率:以2377 Hz 和2843 Hz 两个频率作为特征频率,选取特征频率的1/8、1/4、1/2、1、2 倍率下共10 个频率点。
测试样件包括1 个固壁件和7 个声衬件,固壁件结果作为参考。具体如下:
N1:芳纶纤维复合材料板。其组成为芳纶纤维复合材料不打孔面板(1 件)+玻璃纤维复合材料背板(1 件),翻边高度为26.2(0, –0.3)mm;蜂窝高度为25.2 mm。
N2:芳纶纤维复合材料声衬1。其组成为芳纶纤维复合材料声衬面板(1 件)+玻璃纤维复合材料背板(1 件),面板微孔直径为2 mm,孔中心距为7 mm;相邻三个孔间按照交叉布局执行,两孔形成角度为60°;翻边高度为26.2(0, –0.3)mm;蜂窝高度为25.2 mm。
N3:芳纶纤维复合材料声衬2。其组成为芳纶纤维复合材料声衬面板(1 件)+玻璃纤维复合材料背板(1 件),面板微孔直径为2 mm,孔中心距为7 mm;相邻三个孔间按照交叉布局执行,两孔形成角度为60°;翻边高度为65(0,–0.3)mm;蜂窝高度为64.0 mm。
N4:玻璃纤维复合材料声衬1。其组成为玻璃纤维复合材料声衬面板(1 件)+中间层板(0.5 mm)+玻璃纤维复合材料背板(1 件),面板微孔直径为1.5 mm,孔中心距为3.7 mm;相邻三个孔间按照交叉布局执行,两孔形成角度为60°;翻边高度为65(0, –0.3)mm;中间层板微孔直径为1.8 mm,孔中心距为3.0 mm;相邻三个孔间同样按照交叉布局执行,两孔形成角度为60°;蜂窝高度为25.2 mm+38.3 mm。
N5:玻璃纤维复合材料声衬2。其组成为玻璃纤维复合材料声衬面板+玻璃纤维复合材料背板(1 件),面板微孔直径为l.5 mm,孔中心距为3.7 mm;相邻三个孔间按照交叉布局执行,两孔形成角度为60°;翻边高度为26.2(0,–0.3)mm;蜂窝高度为25.2 mm。
N6:玻璃纤维复合材料声衬3。其组成为玻璃纤维复合材料声衬面板(1 件)+中间层板(0.5 mm)+玻璃纤维复合材料背板(1 件),面板微孔直径为1.5 mm,孔中心距为3.7 mm;相邻三个孔间按照交叉布局执行,两孔形成角度为60°;翻边高度为26.2(0, –0.3)mm;中间层板微孔直径为1.8 mm;孔中心距为3.0 mm;相邻三个孔间按照交叉布局执行,两孔形成角度为60°;蜂窝高度为12.35 mm+12.35 mm。
2 仿真与实验结果与分析
2.1 背景流场计算
利用Fluent 二维轴对称模型进行背景流场计算,边界条件设置和流场计算结果如图4 所示。声源面定义质量流量,根据实验下各个流场状态声源面平均流速、密度和截面积换算出声源面方向出口质量流量。进口总压设为一个1.01×105MPa,出口静压设为一个1.01×105MPa,参考压力设为0,温度设为288 K。为了更好地收敛,先将流体介质定义为不可压缩气体算至收敛后,将流体介质改为理想气体进行计算。通过流场计算得到声源面出口声速、密度和流速,在Actran 中背景流声传播计算中作为输入。

图4 流场计算模型 (a)边界条件;(b)速度云图;(c)压力云图Fig.4 Flow field calculation model (a)boundary conditions;(b)velocity nephogram;(c)pressure nephogram
通过后处理,统计各个流场状态下得到声衬端平均密度,声速和平均流速,结果见表2。计算得到各流场状态下风扇出口的平均速度、密度和声速见表3,在声传播计算中,用来定义声源面边界。
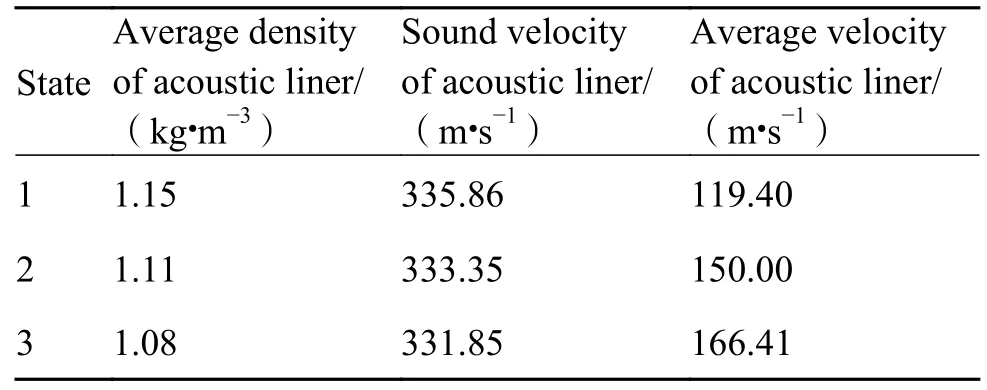
表2 流场结果Table 2 Flow field results

表3 风扇出口流场结果Table 3 Fan outlet flow field results
2.2 声学模型
使用声学仿真软件Actran 进行计算分析,声学仿真模型和边界条件如图5 所示。建模思路为:(1)考虑到模型尺寸、分析频率范围及模型几何特征,项目中使用2D 轴对称模型进行建模计算,建立二维轴对称模型;(2)使用环形管道模态声源定义入射端面。声源端径向模态设置1,周向模态根据不同的实验状态进行设置。不同状态下声源面声功率级换算成声强作为管道模态声源激励;(3)在管道侧壁定义导纳边界条件,模拟不同结构形式的声衬试件;(4)从管道末端建立声传播区域,其外边界定义为声学无限元,用以模拟末端无反射边界条件,在远场距离喇叭口进口中心点21 m 每5°布置一个场点,用于提取远端测点的声学响应。
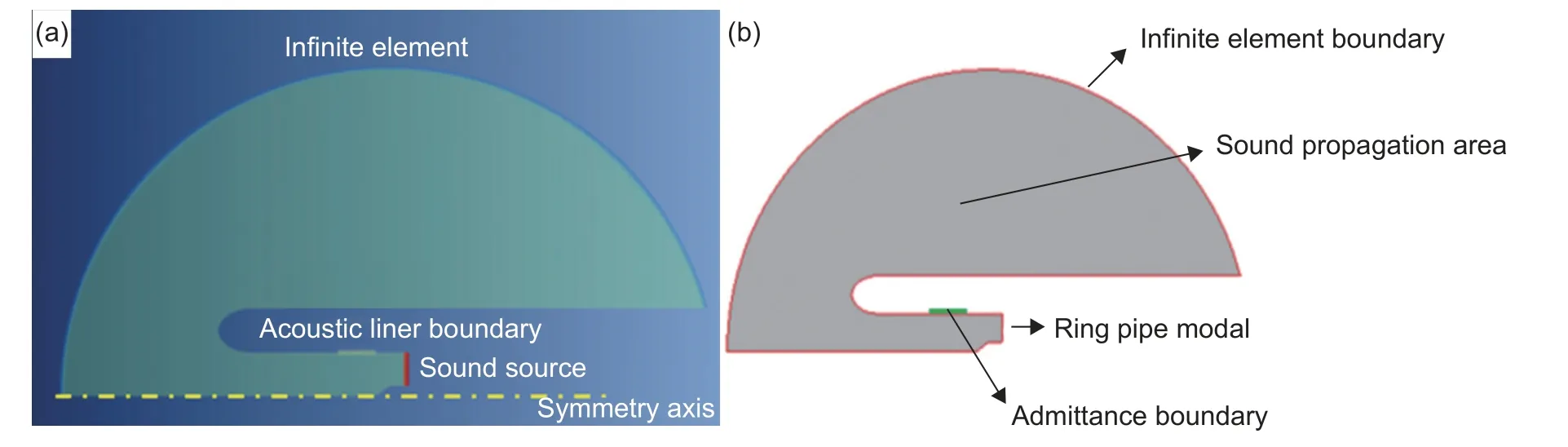
图5 声学仿真模型示意图 (a)无流计算模型;(b)边界条件Fig.5 Schematic diagram of acoustic simulation model (a)calculation model without flow;(b)boundary conditions
其中边界条件设置如下:
声源面:定义环形管道模态,径向模态为1,周向模态根据3 个不同流场状态实验得到的BPF 和2BPF 的周向模态值进行定义;有流条件下,按流场计算得到结果定义声源面速度、声速和密度。
声衬边界:定义导纳边界条件,通过声阻抗模型计算得到不同结构形式的声衬件的声阻抗值。分别采用两种声阻抗模型进行计算分析:(1)Lee&Ih 模型[23]声阻部分和cummings 模型[24]声抗部分组合的复合模型;(2)适用于高马赫数的Goodrich 声阻抗模型[25]。
管道末端建立声传播区,外部边界定义无限元,模拟无反射边界,由于实验是在地面进行,故无限元边界处的飞行速度设为0。
有流条件的声传播计算分为两步:(1)Actran中进行可压缩背景流计算;(2)将背景流场计算结果通过ICFD 插值到声学网格上,进行声传播计算。
在Actran 中进行可压缩背景流计算,边界条件设置和计算结果见图6。声源面设置速度边界,速度值前文Fluent 流场计算结果已给出,出口速度为0,进口速度为0。
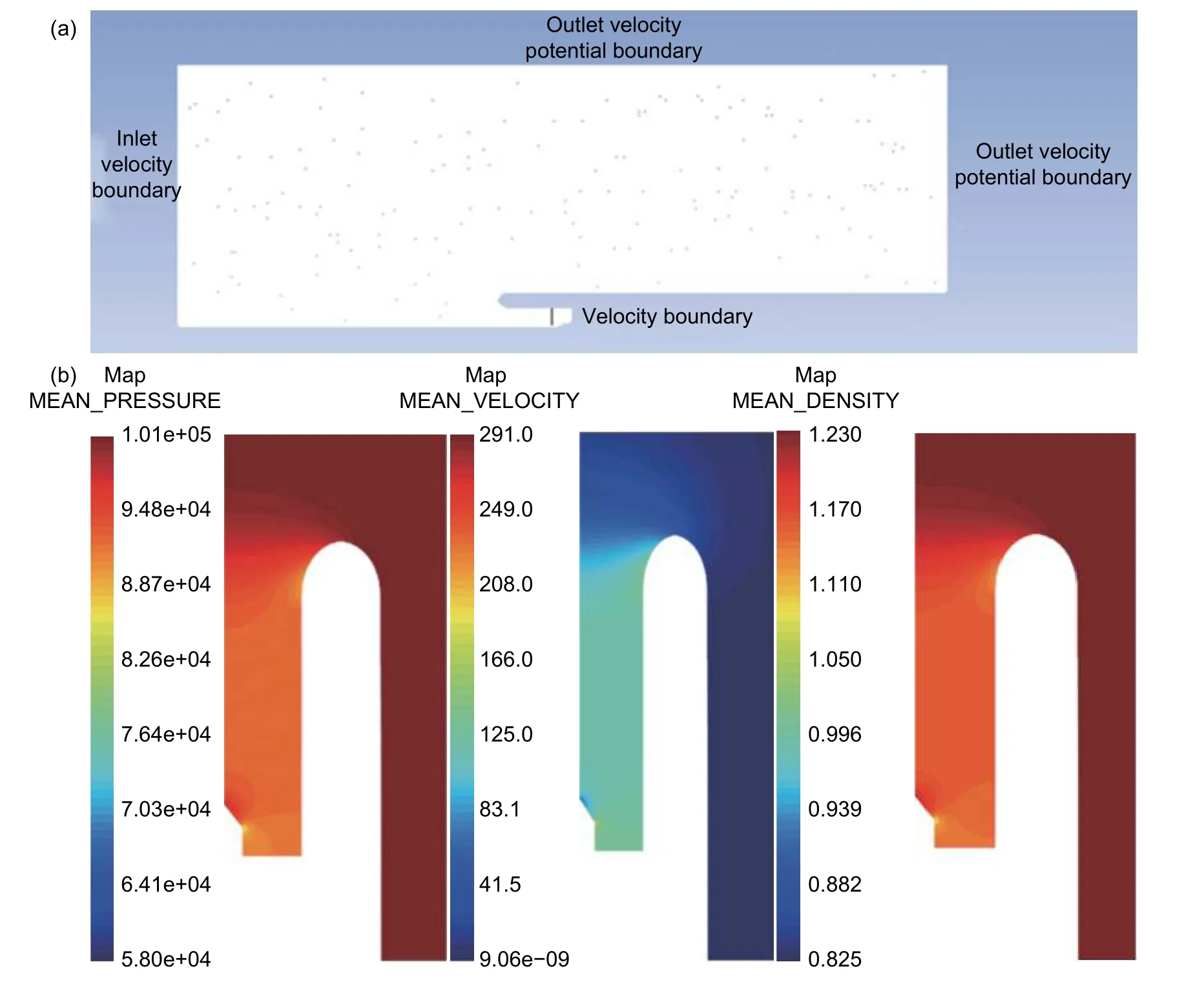
图6 Actran 背景流场计算 (a)边界条件;(b)计算结果Fig.6 Calculation of Actran background flow field (a)boundary conditions;(b)calculation results
背景流场计算完成后,将得到的流场结果利用ICFD 插值到声学网格上,结果如图7 所示。
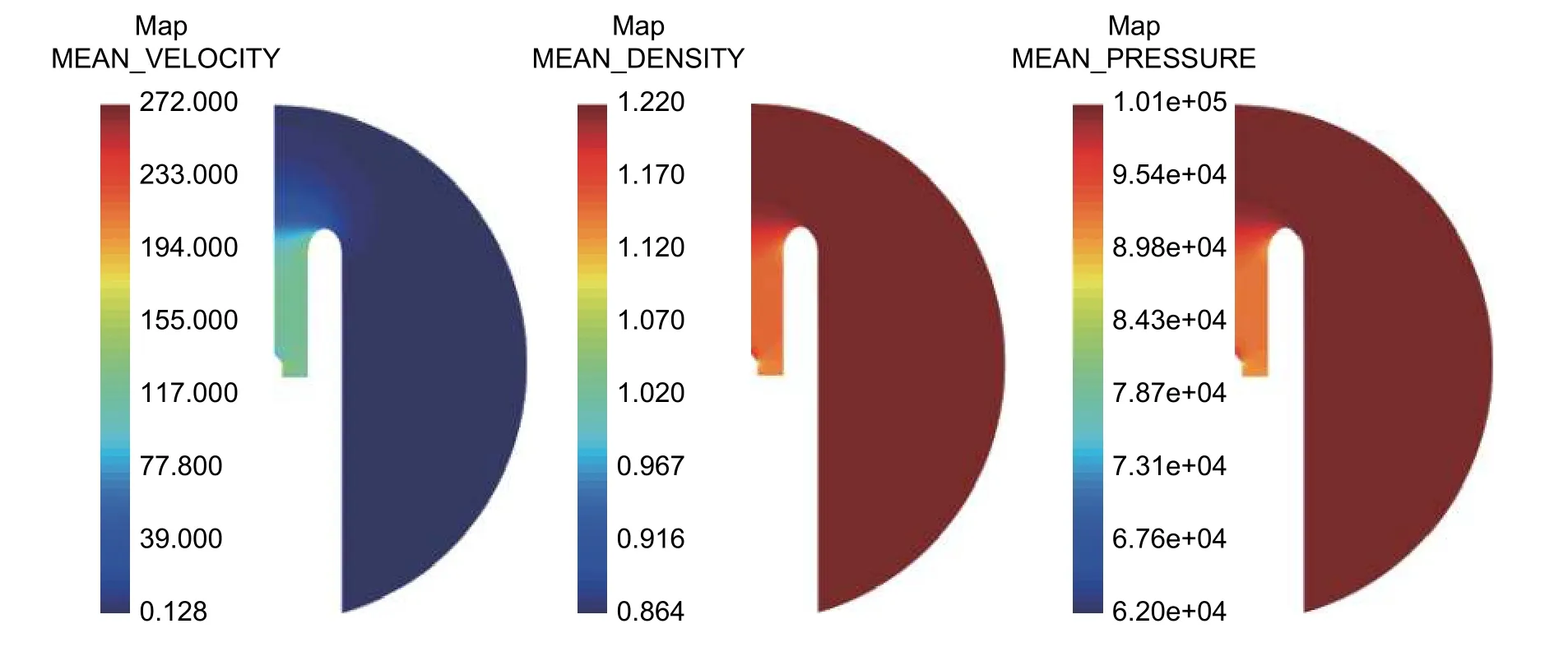
图7 背景流场插值结果示例Fig.7 Examples of background flow field interpolation results
流场数据映射到声学网格上之后进行声传播计算,有流条件声传播与无流条件设置区别在于:
(1)声源面按流场计算结果设置流速;
(2)按流场计算结果得到的密度和声速定义声源面流体材料;
(3)声传播区增加ICFD 插值后的流场结果。
2.3 声阻抗模型比较
以流场工况1 和工况2,消音板孔间距为7 mm,厚度1.2 mm,消音孔直径为2 mm,蜂窝厚度为25.2 mm 声衬为例,对比两个声阻抗模型差异。图8为两种工况分别在不同声模态激励下采用Goodrich 模型和Lee&cummings 复合声阻抗模型计算得到的传递损失对比。其中传递损失TL又称透射损失,定义为声衬进口端声功率级与出口端声功率级之差。
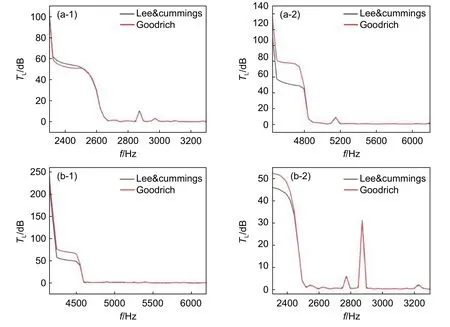
图8 不同工况下不同声阻抗模型传递损失对比(a)工况1;(b)工况2;(1)声模态(22,1);(2)声模态(44,1),Fig.8 Comparison of transmission loss of different acoustic impedance models in different working conditions(a)working condition 1;(b)working condition 2;(1)mode(22,1);(2)mode(44,1)
式中:w1为入射声功率;w2为透射声功率;Lw1为入射声功率级;Lw2为透射声功率级。
由于声衬进口端和出口端通道截面相同,声压沿截面近似均匀分布,传递损失=进口端声压级-出口端声压级。
式中:p1为入射声压;p2为透射声压;Lp1为入射声压级;Lp2为透射声压级。
由图8(a)可看出,工况1 在两种声模态激励下,两个阻抗模型传递损失的频谱特性较为相似,符合亥姆霍兹共振器的典型特征,即在共振频率处传递损失最大,而在其他频率处传递损失几乎为零。这是由于声衬采用的共振式吸声原理,其结构决定只对特定频率的噪声敏感,故在共振区间内吸声效果较为明显,当噪声频率与声衬固有频率差别较大时,声波穿过管道时几乎没有衰减,入口与出口处声压级基本保持一致。在(22,1)阶声模态2500 Hz 以下两个阻抗模型传递损失差值在3 dB左右,2500 Hz 以上两者很接近,在目标频率2377 Hz(BPF)处两者相差3 dB。在(44,1)阶声模态4800 Hz以下两个阻抗模型传递损失差距25 dB,4800 Hz以上差值很小,在5000 Hz 左右传递损失接近0 dB,在目标频率4754 Hz(2BPF)处两者相差23 dB。
由图8(b)可以看出,工况2 在两种声模态激励下两个阻抗模型传递损失频谱特性也较为相似,除对与共振频率相近频率的噪声具有明显的抑制作用以外,对其他频率的噪声几乎不具有抑制作用,具有明显的噪声频率选择特性。(22,1)阶声模态在目标频率2843 Hz(BPF)处,两者传递损失都接近于0 dB。(44,1)阶声模态在目标频率5687 Hz(2BPF)处,两者传递损失都接近0 dB。
2.4 仿真参数
根据模态声功率测量结果,工况3 下BPF(3060 Hz)下的(22,1)模态声功率级为174 dB,比其余工况声模态声功率级都高,声衬参数影响研究主要针对该流场工况BPF(3060 Hz)下的声模态,该状态下相关实验参数如表4 所示。
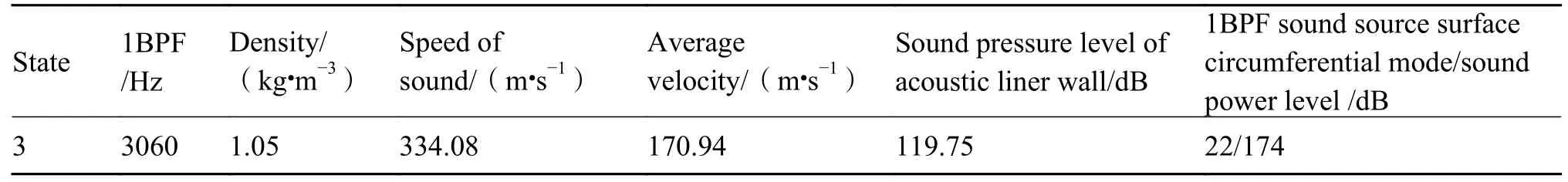
表4 实验状态参数Table 4 Test state parameters
以结构参数如下表5 所示的声衬为基础,在其他结构参数不变的情况下,分别研究双单自由度声衬和双自由度声衬在不同消音孔间距、不同消音孔直径、不同穿孔板厚度、不同蜂窝高度对吸声性能的影响,各参数取值见表6,声阻抗模型采用Goodrich模型。

表5 声衬结构参数Table 5 Acoustic liner structure parameters

表6 声衬结构参数变化Table 6 Variation of acoustic liner structure parameters
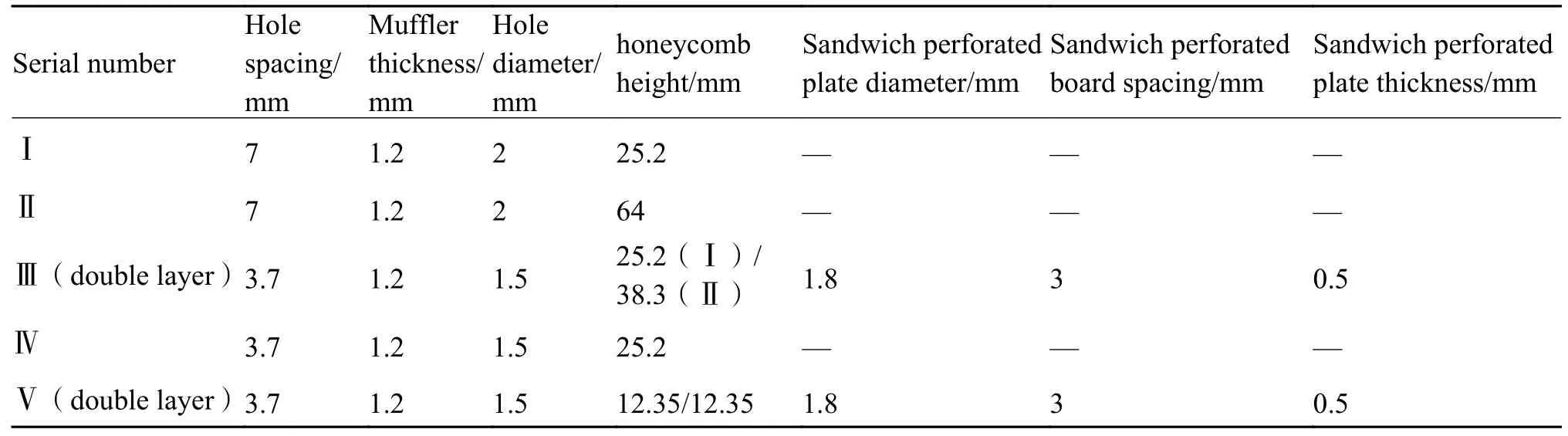
表7 平板试样参数明细Table 7 Details of parameters of flat samples
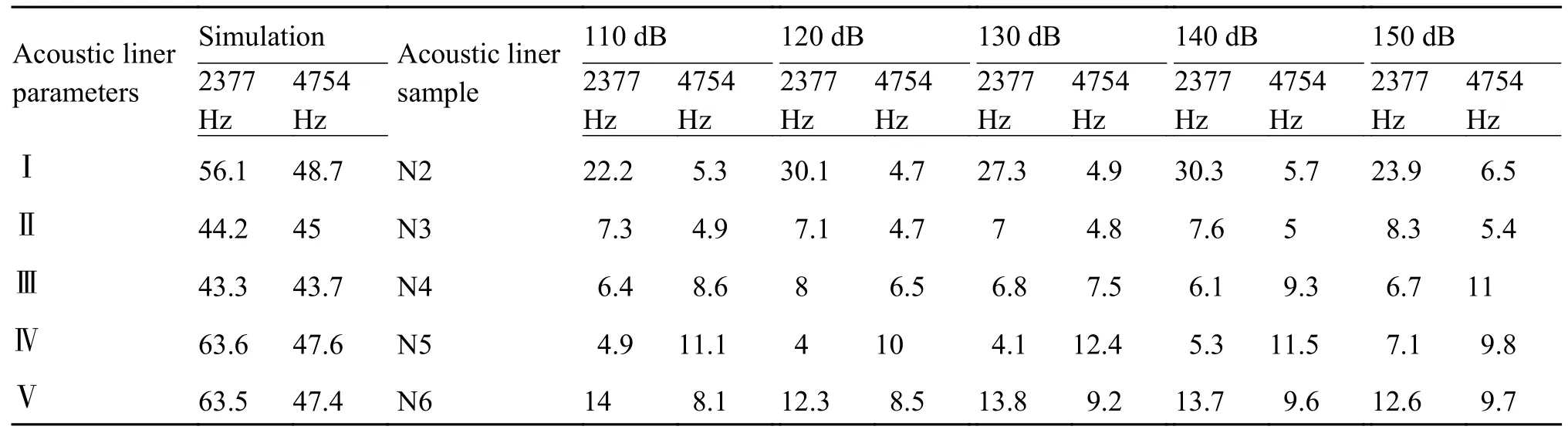
表8 传递损失对比Table 8 Transmission loss comparison
2.5 单自由度声衬结构参数对吸声性能影响
图9 为单自由度声衬结构参数对声衬耗散功率的影响。由图9(a)看出,整体趋势为消音板直径越小,声衬耗散功率越大。在目标频率BPF(3060 Hz)处,1.5 mm 直径穿孔声衬耗散功率最大,吸声性能最好。这是由于穿孔直径减小,孔径壁对传来的声音产生的阻尼和摩擦作用增强,使传来的声能得到衰减,能量降低,吸声性能得到提高。但同时穿孔直径越小,加工越困难,导致生产成本增加,所以对于穿孔直径的选择,应结合生产成本和吸声性能综合考虑。
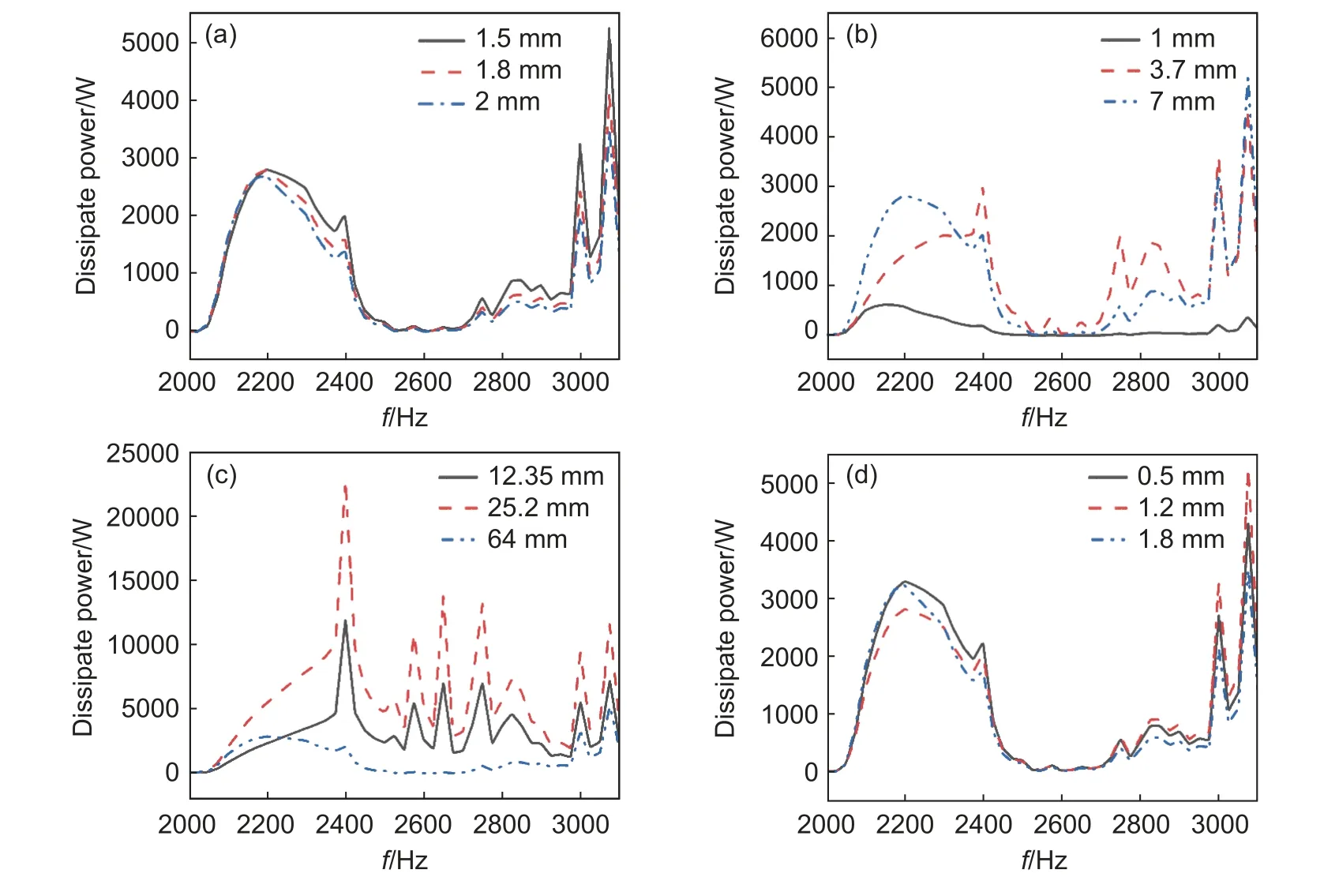
图9 单自由度声衬结构参数对声衬耗散功率的影响 (a)消音板直径;(b)孔间距;(c)蜂窝高度;(d)消音板厚度声Fig.9 Influence of structural parameters of SDOF acoustic liner on the dissipated power of acoustic liner (a)muffler diameters;(b)hole spacing;(c)honeycomb heights;(d)muffler thickness
由图9(b)可知,孔间距为1 mm 的声衬耗散功率在2000~3100 Hz 频率范围最小,3.7 mm 孔间距在低频和高频时吸声性能最好,耗散功率最大。目标频率BPF(3060 Hz)处,3.7 mm 孔间距声衬耗散功率最大,7 mm 孔间距次之,1 mm 孔间距声衬耗散功率最小。通过对比可以发现声衬的吸声性能并不随孔间距大小呈现线性变化,在不同频率处有着不同的吸声效果,故提高声衬吸声性能应在相应的目标频率下选择合适的孔间距。
由图9(c)看出,目标频率BPF(3060 Hz)处,64 mm 蜂窝高度声衬耗散功率最小,25.2 mm 蜂窝高度声衬耗散功率最大,吸声性能最好。而在其他频率处,声衬同样遵循着这样的规律,尤其在2400 Hz 处,25.2 mm 蜂窝高度声衬表现出极为优异的吸声效果。
由图9(d)看出,三种不同厚度的消音板(0.5、1.2、1.8 mm)表现出相似的吸声效果与变化规律。而1.2 mm 消音板厚在目标频率BPF(3060 Hz)耗散功率最大,吸声效果最好。
2.6 双自由度声衬结构参数对吸声性能影响
图10 为双自由度声衬结构参数对声衬耗散功率的影响。由图10(a)看出,孔直径在1.5~2 mm范围内,消音板孔直径越小,声衬耗散功率越大。在目标频率BPF(3060 Hz)处1.5 mm 声衬耗散吸声性能最好。不同孔直径的消音版声衬(1.5、1.8、2 mm)呈现相似的吸声特征,而整体规律为消音板直径越小,声衬耗散功率越大。在目标频率BPF(3060 Hz)处1.5 mm 声衬耗散吸声性能最好。
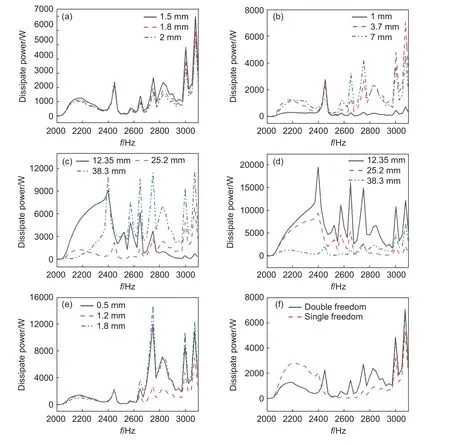
图10 双自由度声衬结构参数对声衬耗散功率的影响 (a)消音板直径;(b)孔间距;(c)第Ⅰ层蜂窝高度;(d)第Ⅱ层蜂窝高度;(e)消音板厚度;(f)自由度Fig.10 Influences of structural parameters of DDOF acoustic liner on dissipated power of acoustic liner (a)muffler diameters;(b)hole spacing;(c)level Ⅰ honeycomb heights;(d)level Ⅱ honeycomb heights;(e)muffler thickness;(f)degree of freedom
由图10(b)可知,不同消音板间距在不同频率段有着不同的吸声效果,其中1 mm 消音板间距声衬在2450 Hz 处具有一定的吸声效果,其余频率处吸声效果较差。而在目标频率BPF(3060 Hz)与3000 Hz 处,3.7 mm 消音板间距声衬耗散功率最大。
由图10(c)可知,在2800 Hz 以上,第Ⅰ层蜂窝高度越大,声衬耗散功率越大,吸声效果越好。而在目标频率BPF(3060 Hz)处,第Ⅰ层蜂窝高度为38 mm 的声衬吸声效果最好。图10(d)显示的是第Ⅱ层蜂窝高度对吸声效果的影响,其中12.35 mm蜂窝高度的声衬在2000~3100 Hz 耗散功率最大,表现出了最好的吸声效果。
由图10(e)看出,2500 Hz 以下频率处不同消音板厚度(0.5、1.2、1.8 mm)声衬耗散功率较为相似,而在2500 Hz 以上1.8 mm 消音板厚度声衬耗散功率最大,1.2 mm 厚度的耗散功率明显低于其他两种厚度声衬,表现出最差的吸声效果。而目标频率BPF(3060 Hz)处,1.8 mm 厚度耗散功率最大,吸声性能好。
图10(f)为不同自由度声衬耗散功率对比图。如图10(f)所示,对比了相同消音孔间距、孔直径、板厚度和蜂窝高度单自由度和双自由度声衬耗散功率。在其他结构参数相同时,2500 Hz 以上双自由度声衬耗散功率较大,明显优于单自由度声衬,吸声效果好。
2.7 仿真与实验结果对比
将流场状态Ⅰ特征频率BPF、2BPF 下各个声衬仿真与实验的传递损失进行对比,流场状态Ⅰ参数如表1 所示。根据实验的声衬参数,声衬Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ别对应实验声衬样件N2、N3、N4、N5、N6。
从实验结果来看,声压级对声衬传递损失影响较大,尤其是样件N2,仿真与实验传递损失结果差异比很大,主要有以下几点原因:
(1)模型尺寸:仿真模型为直径1048.8 mm、总长1968.7 mm 的二维轴对称圆形管。实验为70 mm ×100 mm 的矩形流管。
(2)声衬布置方式:仿真声衬长452.2 mm,沿流管环形布置一圈。实验为520 mm ×100 mm 的平板声衬样件。
(3)声源激励:仿真在2377 Hz 处,声源激励为22 阶周向管道模态,声功率级165 dB,在4754 Hz,声源激励为44 阶周向管道模态,声功率级164 dB。实验在2377 Hz 和4754 Hz 声源激励为SPL=110、120、130、140、150 dB 五个声压级。
(4)评价方法:仿真采用声衬进口入射声功率级与出口端无限元透射声功率级之差计算传递损失,实验采用四传声器法得到样件传递损失。
特征频率不同倍率下的仿真和实验传递损失对比结果见图11。由于仿真模型管道模态波求解频率为1675 Hz,激励频率在1675 Hz 以下时,管道的截止效应导致该阶模态波迅速衰减消失,无法在管道中进行传播,因此在1675 Hz 以下得到的仿真传递损失为0(实验矩形流管高阶声模态截止频率约为1700 Hz)。其余频率点仿真与实验的传递损失最大误差在4 dB 以内。
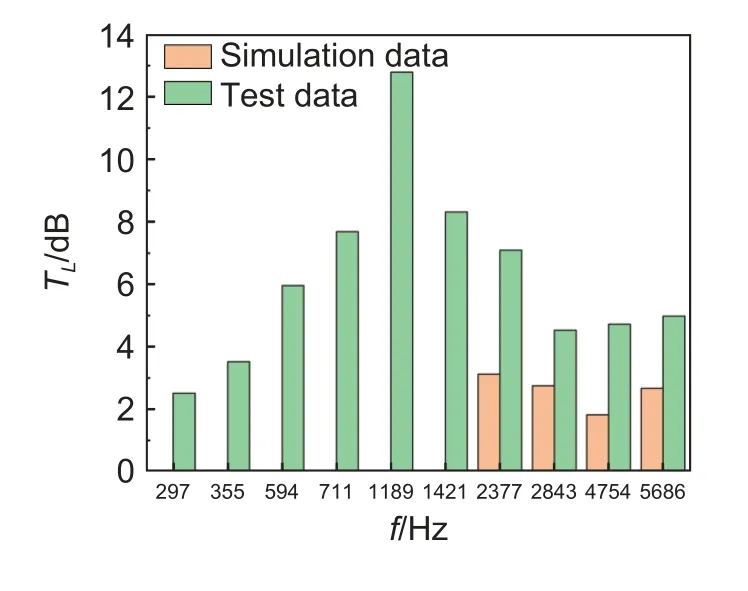
图11 传递损失对比Fig.11 Transmission loss comparison
误差来源主要有:
(1)仿真声衬的阻抗值通过理论公式计算得到,与实验值存在一定偏差;
(2)仿真可以直接得到流管进出口声功率,传递损失通过进出口声功率计算得到,实验采用四传声器法测量传递损失,评价方法有一定差异;
(3)测试中有不可避免的误差产生。这包括声衬制造误差和流管装置误差两方面:声衬内为纸蜂窝,其蜂窝腔没有与穿孔板上的小孔一一对应,某些小孔恰好被纸蜂窝分隔或挡住;且有些声衬表面有细微的弯曲弧度,不是理想的平面,无论对于声场还是流场,都有一定的影响。
3 结论
(1)计算了不同流场状态下管道模态声源特征,并以此作为Actran 软件背景流场计算及声传播计算的输入边界,考虑到结构模型几何特征及分析频率,结构仿真使用Actran 软件中二维轴对称模型进行。通过以上声学模型的建立,对比分析了不同声模态激励下、不同声阻抗模型的传递损失。
(2)仿真计算研究,对于两种自由度声衬,孔直径在1.5~2 mm 范围内,穿孔直径越小,则吸声性能越好。孔间距、蜂窝高度和消音板厚度在对吸声性能的影响随频率变化,在目标频率BPF(3060 Hz)处,针对单自由度声衬,1.5 mm 孔直径、3.7 mm 孔 间 距,25.2 mm 蜂 窝 高 度 声 衬 和1.2 mm消音板厚耗散功率最大。而对于双自由度声衬,3.7 mm 孔间距耗散功率最大,第Ⅰ层蜂窝高度38 mm 的声衬吸声效果最好,12.35 mm 第Ⅱ层蜂窝高度耗散功率最大,1.8 mm 消音板厚耗散功率最大。
(3)通过声衬中不同结构参数对吸声效果影响的仿真模拟,得到不同结构声衬在不同激励源下的传递损失,给出了一套合理可信的仿真方法。根据此方法可以进一步计算其他结构参数对声衬的吸声效果的影响,大大节省了声衬实验探索成本。
