装配式双拼槽钢-混凝土组合梁抗剪承载力试验研究
2023-10-13周凌宇石敬州李分规戴超虎徐增武廖飞蒋卫朱志辉
周凌宇,石敬州,李分规,戴超虎,徐增武,廖飞,蒋卫,朱志辉
(1. 中南大学 土木工程学院,湖南 长沙,410075;2. 中南大学 高速铁路建造技术国家工程研究中心,湖南 长沙,410075;3. 中建五局第三建设有限公司,湖南 长沙,410004)
钢-混组合梁具有自身质量小、承载力高、刚度大的优点,在建筑和桥梁结构领域的应用越来越广泛[1]。装配式组合梁在满足刚度要求的情况下具有施工速率高、湿作业量小、节能环保的优势。国内外学者对装配式钢-混组合梁的抗弯性能[2-6]和纵向抗剪[7-9]性能进行了深入研究,但对其竖向抗剪性能的研究很少[10-11]。目前,人们对现浇工字形钢梁组合梁的竖向抗剪研究已取得一些成果[12-18]。聂建国等[12-14]对16根紧凑型钢-混凝土组合梁进行试验,发现组合梁破坏形态不仅与组合截面的剪跨比有关,而且受到钢梁剪跨比的影响,提出了考虑混凝土影响的紧凑截面组合梁正弯矩和负弯矩下的抗剪承载力公式。VASDRAVELLIS 等[15]对14根组合梁和1根钢梁进行了弯曲和剪切试验,研究分析了弯剪相互作用规律,发现当作用剪力超过组合截面抗剪强度的60%时,组合梁的抗弯承载力开始降低。丁发兴等[17]在工字钢-混凝土组合梁试验的基础上进行了有限元参数分析,确定了工字钢-混凝土组合梁弯剪破坏与受弯破坏的界限剪跨比λ=3,提出了考虑混凝土板组合作用系数和钢梁翼缘板贡献的组合梁的抗剪承载力计算公式。
可见,研究者们提出的抗剪承载力计算公式能够较好地预测组合梁抗剪承载力,但仅适用于传统组合梁,具有很大的局限性。与工字形钢梁组合梁相比,装配式组合梁截面形式往往不同,导致抗剪性能存在差异,其混凝土板的抗剪承担比例不明确,使用规范和现有公式进行相关设计应用适用性差。本文提出一种装配式双拼槽钢-混凝土组合梁,由槽钢焊接加劲肋和钢板抗剪连接件,浇筑混凝土梁板形成预制模块,通过高强螺栓连接,如图1所示。组合梁混凝土板位于钢梁上翼缘下方,能够降低梁高,增大建筑物使用空间,具有广阔的应用前景。在剪跨比较小时,竖向剪力起控制作用,有必要对双拼槽钢-混凝土组合梁竖向抗剪性能进行研究。本文基于双拼槽钢-混凝土组合梁的试验结果,使用ABAQUS 有限元软件开展组合梁抗剪性能参数化分析,根据叠加原理提出双拼槽钢-混凝土组合梁竖向抗剪承载力计算方法。
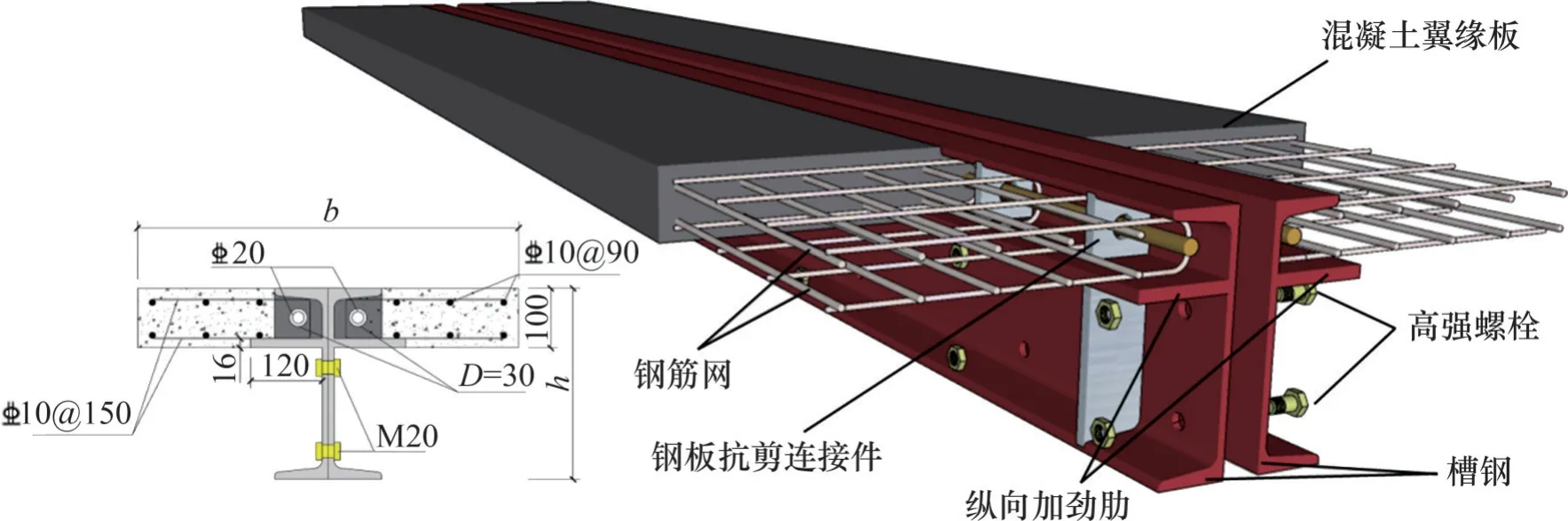
图1 双拼槽钢-混凝土组合梁Fig. 1 Double-channel steel-concrete composite beam
1 试验结果与分析
对7 根双拼槽钢-混凝土组合梁的破坏模式、极限承载能力及变形刚度进行研究,分析组合梁受力机理及各参数对极限承载力的影响规律。在试验基础上对组合梁竖向抗剪性能进行研究。
1.1 试验参数
组合梁主要研究参数如表1所示,其中,混凝土板厚度hc为100 mm,混凝土板宽bc分别为600、800、1 000 和1 200 mm;槽钢型号选用32b 和40b,抗剪连接件间距分别为250 mm 和750 mm。采用跨中两点对称单调静力加载,如图2 所示(其中,Pu为荷载)。混凝土板强度等级选用C30,材性试验测得弹性模量Ec=3.00×104MPa,抗压强度fc=34.94 MPa,抗拉强度ft=2.5 MPa。组合梁钢材性能如表2所示。
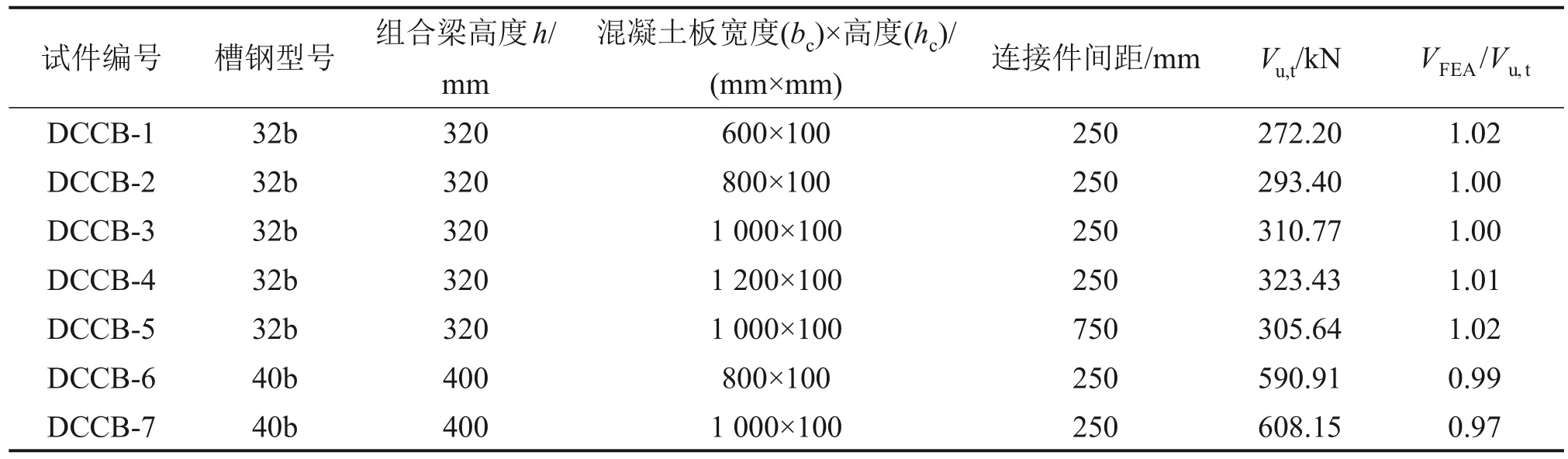
表1 组合梁试件参数及抗剪承载力对比Table 1 Comparison of composite beam specimen parameters and shear capacity
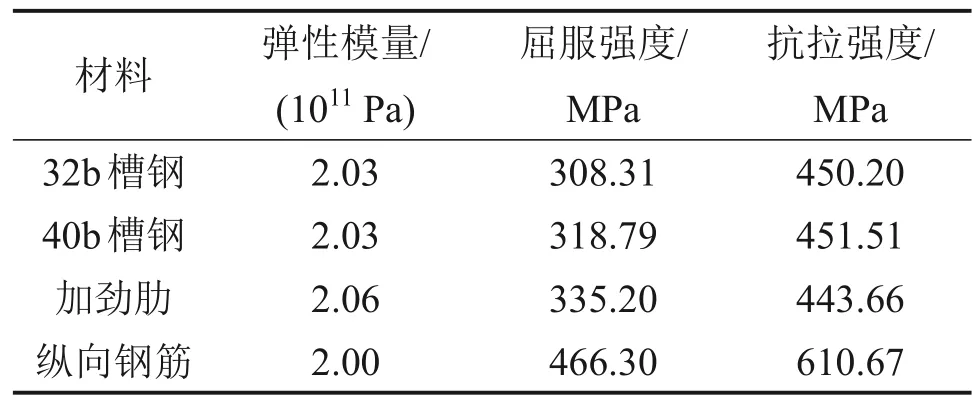
表2 钢材性能Table 2 Steel material properties

图2 加载示意图Fig. 2 Loading conditions
1.2 剪力-跨中挠度曲线
双拼槽钢-混凝土组合梁剪力-挠度曲线如图3所示。从图3可见:组合梁抗剪承载力随着混凝土翼缘板宽度增大而增大;对于构件DCCB-1、DCCB-2、DCCB-3 和DCCB-4,当板宽由600 mm增大至1 200 mm 时,抗剪承载力提高了25.14%;增加抗剪连接件间距,抗剪承载力仅提高1.8%,说明抗剪连接件可有效连接钢梁与混凝土板,适当增大抗剪连接件间距对承载力影响不大,此组合梁的组合作用较强。
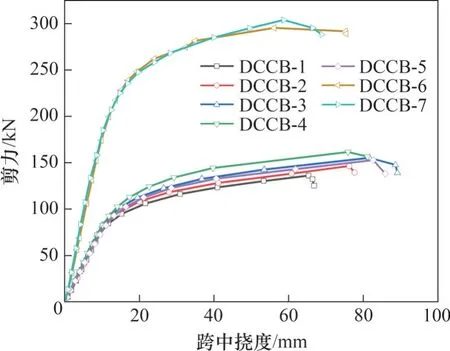
图3 剪力-跨中挠度曲线Fig. 3 Shear-mid-span deflection curves
1.3 荷载-垂直剪应力曲线
在试件剪跨区中部测量槽钢腹板、混凝土板剪切应变。由于构件的破坏模式相同,故仅以试件DCCB-1为例,分析组合梁1/4跨处剪力-应力关系曲线,如图4所示(其中S1、S2、S3、S4分别为钢梁应变测点,C1为混凝土板应变测点)。从图4 可见:在加载初期,测点S2、S3、S4的剪力-剪应力曲线呈线性上升,S1和C1应变以相同的速率呈线性变化,腹板下部的剪应变发展速率大于上部的剪应变发展速率;当荷载达到极限荷载的35%左右时,钢梁腹板的剪应变发展速率提高,S1应变增大而C1应变减小。这是因为钢梁腹板和混凝土翼缘板交界面达到极限黏结强度,自然黏结作用被破坏,钢梁腹板承受了更多剪力。组合梁在进入弹塑性阶段后应力重新分布,中性轴上移,混凝土板和高度为H1的钢梁腹板承受更多剪力。当荷载达到极限荷载的80%后,S1和C1处剪应变发展速率急速上升。由S3和S4的应变发展程度可知,钢梁腹板在极限抗剪承载力下未进入全截面屈服状态。
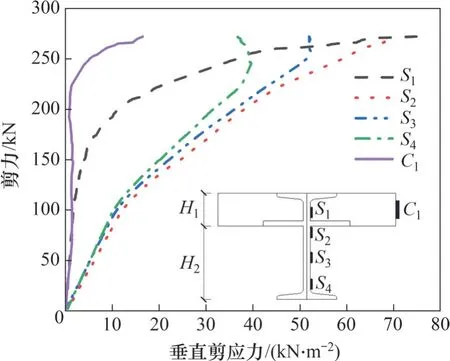
图4 DCCB-1剪力-剪应力关系曲线Fig. 4 Shear-shear stress curve of DCCB-1
1.4 剪切应变分布规律
在不同荷载下,沿钢梁腹板高度测量点的剪应变分布规律如图5所示,图中曲线是以双槽钢为整体按式(1)[19]计算得到的剪切应变曲线,散点为实测剪切应变。从图5可见,实测剪切应变与按式(1)计算得到的剪切应变基本吻合,这表明高强螺栓连接的双拼槽钢协同工作良好,整体抗剪性能优异。

图5 DCCB-1沿截面高度剪应变分布规律Fig. 5 Distribution law of shear strain of DCCB-1 along section height
式中:FS为截面上的剪力;Iz为整个截面对中性轴的惯性矩;Sz*为截面上测点以下部分的面积对中性轴的静矩;b0为腹板宽度;E为钢材弹性模量。
数值分析结果表明:当加载至极限抗剪承载力时,H2腹板承担了组合梁85%左右的剪力,H1腹板承担了组合梁11%左右的剪力,混凝土在组合梁弯曲破坏模式下承担了约4%的剪力。与传统组合梁[12]相比,双拼槽钢-混凝土组合梁混凝土板位于钢梁翼缘下部,钢梁腹板和混凝土板协同受力,混凝土板抗剪承担比例减小,降低了在局部剪力较大时混凝土板发生剪切脆性破坏的风险,组合梁的抗剪性能提高。但仅据7根组合梁的试验结果还不能得出经验公式,下面通过有限元模型参数化分析,研究不同剪跨比的组合梁抗剪性能。
2 ABAQUS分析模型
2.1 建模方法
通过ABAQUS建立双拼槽钢-混凝土组合梁有限元计算模型,模型边界条件按加载试验的简支梁约束,采用增量迭代法进行非线性分析。
钢梁的翼缘、腹板和加劲肋采用4节点线性减缩积分有限薄膜应变壳单元(S4R),沿厚度方向取5 个积分点,网格长×宽为40 mm×40 mm。混凝土板采用8 节点等参三维线性减缩积分实体单元(C3D8R),网格长×宽×高为40 mm×40 mm×40 mm。钢筋采用三维线性桁架单元(T3D2),上下层钢筋网由分布钢筋合并而成,以模拟钢筋的绑扎效果;钢筋网通过内置区域嵌于混凝土,模拟钢筋网在混凝土板内协同工作的性能,钢筋网网格长×宽×高为50 mm×50 mm×50 mm。组合梁2 个预制模块螺栓连接处采用tie 连接方式。混凝土板与槽钢、加劲肋、抗剪连接件之间法线方向相互作用采用“硬接触”,允许接触后分离,切线方向相互作用采用面与面接触,定义为“罚”,摩擦因数为0.4,用于模拟组合梁中钢梁翼缘、腹板和混凝土翼缘板的黏结作用。
2.2 本构关系
考虑材料非线性和几何非线性,根据GB 50010—2010《混凝土结构设计规范》[20]确定钢材和混凝土的应力-应变关系。
钢梁和钢筋采用双折线本构模型,材料特性见表2,钢材本构曲线见图6(a)。图6中:fy为钢材屈服强度;fu为钢材极限强度;σs为钢材应力;εy为钢材屈服时的应变;εu为钢材达到极限强度的应变。

图6 钢材和混凝土本构曲线Fig. 6 Constitutive curves of steel and concrete
式中:εs为钢材应变;Es为钢材的弹性模量;k为钢材硬化段斜率,k=(fu-fy)/(εu-εy)。
混凝土采用塑性损伤模型(CDP),弹性模量Ec=3.00×104MPa,混凝土受拉/压应力-应变曲线见图6(b)。混凝土单轴受拉本构关系如下:
式中:dt为单轴受拉损伤演化参数;ρt=ft,r/(Ecεt,r);ft,r为混凝土单轴极限拉应力,取试验值2.5 N/mm2;εt,r为混凝土单轴极限拉应变,取规范值107×10-6;αt为混凝土单轴受拉应力-应变参数,C30 混凝土取1.95。
混凝土单轴受压本构关系表达式为
式中:dc为单轴受压损伤演化参数;Ec为混凝土弹性模量;n=Ecεc,r/(Ecεc,r-fc,r);ρc=fc,r/(Ecεc,r);x=ε/εc,r;fc,r为混凝土单轴极限压应力,取试验值34.94 N/mm2,εc,r为混凝土单轴极限压应变,取规范值1 720×10-6;αc为混凝土单轴受压应力-应变参数,C30混凝土取1.65。图6(b)中,εcu为应力应变曲线下降段应力等于0.5fc,r时的混凝土压应变,εcu/εc,r取2.10。
2.3 模型验证
以DCCB-2和DCCB-6为例,双拼槽钢混凝土组合梁的试验与模拟的剪力-跨中挠度曲线如图7所示。由图7可见:有限元模型预测的组合梁刚度与试验梁的刚度在70%极限荷载前基本相同。各个试验梁的极限承载力的对比结果见表1,平均相对误差为1.47%,标准偏差为1.84%,模型预测值与试验值之间的相对误差在10.00%以内。组合梁DCCB-6的试验破坏形态和有限元模型破坏时的应力云图如图8所示。通过有限元分析结果验证试验观察的组合梁纯弯段混凝土板顶部压碎破坏模式,发现本文模型能够较准确地模拟组合梁的初始刚度以及弯剪强度,因此,所建立的有限元模型可用于双拼槽钢-混凝土组合梁的抗剪强度分析。

图7 组合梁有限元模拟结果与试验结果的比较Fig. 7 Comparison of finite element calculated values and test values of composite beams

图8 试验破坏形态和有限元应力云图对比Fig. 8 Comparison between test failure and finite element method
3 参数分析
采用前面经验证的建模方式和材料本构关系对组合梁的参数进行分析。首先考虑剪跨比的影响,剪跨比λ=a/h,其中,a为剪跨长度,h为梁高度。材料强度和组合截面尺寸对组合梁的承载力均有一定影响。为探究不同破坏模式下钢梁腹板强度fs和混凝土强度fc、钢梁腹板宽度×高度(tw×hw)、混凝土板宽度×高度(bc×hc)对组合梁承载力的影响,采用λ为0.20、1.25 和2.50 这3 种剪跨比的组合梁模型进行参数化分析。组合梁有限元分析参数变化见表3。

表3 有限元分析参数变化Table 3 Variation of finite element analysis parameters
3.1 剪跨比
剪跨比是影响组合梁抗剪承载力的重要因素。以试件DCCB-2 和DCCB-6 为基础建立有限元模型。计算中,保持梁跨L=4 000 mm,改变组合梁加载位置以调整剪跨比,研究不同剪跨比的组合梁的抗剪承载力的变化规律。
图9所示为不同剪跨比下的组合梁剪力和弯矩的变化规律。从图9可见:
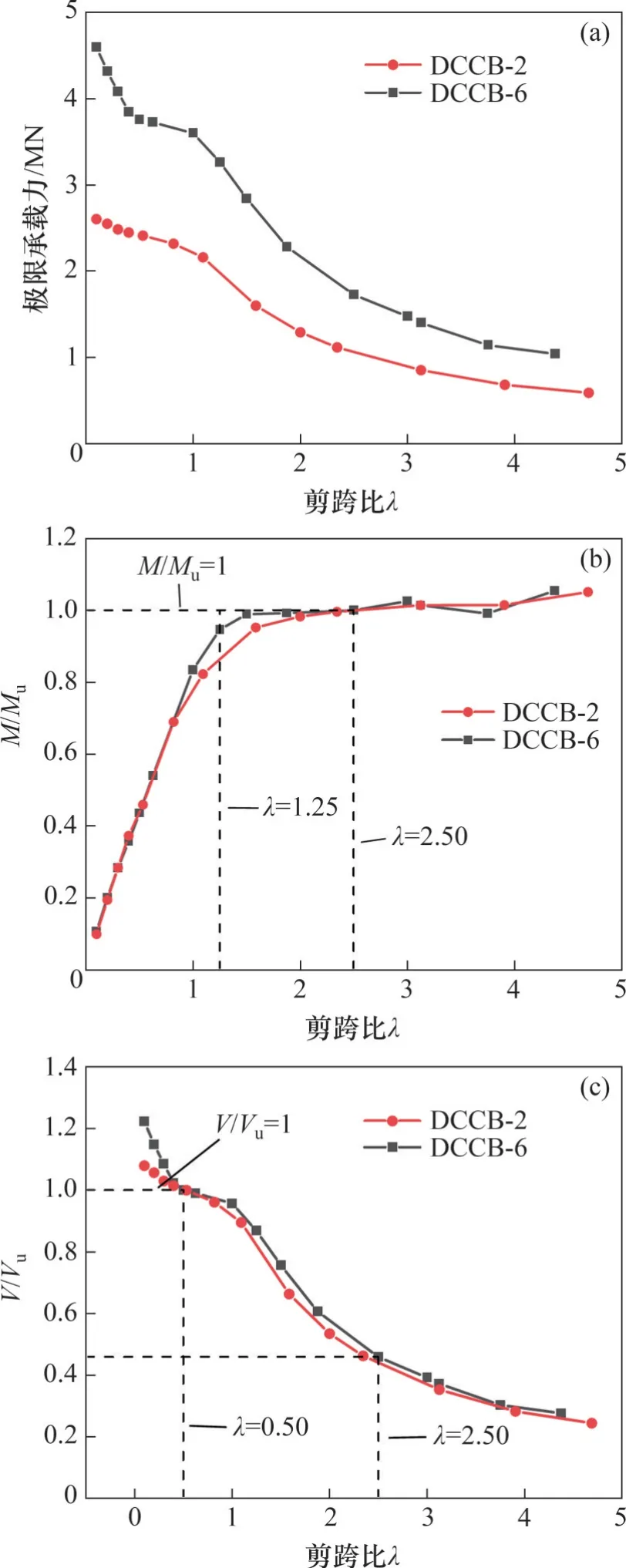
图9 不同剪跨比下组合梁剪力和弯矩的关系曲线Fig. 9 Relationship curves of shear and bending moment of composite beams with different shear-span ratios
1) 当λ≤0.50 时,随着剪跨比减小,组合梁抗剪承载力快速上升。这是因为混凝土板逐步由剪压破坏转为倾向于斜压破坏,且当剪跨较小时,抗剪连接件、上翼缘和纵向加劲肋对混凝土板有双轴围压的作用使得结构具有更高的抗剪承载力。此时,模型的破坏以剪跨段混凝土板纵向剪切开裂以及钢梁支座处屈曲为主要特征。
2) 当0.5<λ<2.5 时,随着剪跨比增加,抗剪承载力下降平缓,结构出现纯弯段混凝土压碎的特征,因此,认为λ=0.50 是组合梁剪切破坏和弯剪破坏的界限剪跨比。当λ=1.25时,组合梁抗剪承载力V与极限抗剪承载力Vu的比值为0.5~0.8,组合梁弯矩M与极限弯矩值Mu比值超过0.9,M/Mu-λ关系曲线上升趋势变缓,此时,主要以跨中混凝土翼板压碎为特征,抗剪不再起主导作用。
3) 当λ≥2.50 时,跨中截面钢梁首先达到屈服应变,随着荷载的增加,纯弯段中部混凝土翼缘板顶部横向裂缝逐渐增多、扩展,在极限荷载时,纯弯段顶部混凝土被压碎,此时,组合梁弯矩M几乎达到Mu。因此,将λ=2.5作为组合梁弯剪破坏与弯曲破坏的界限剪跨比。
3.2 弯剪相互作用
通过对不同剪跨比的组合梁进行非线性分析,研究组合梁弯剪破坏时弯矩-剪力相互作用强度。
当有限元模拟的剪跨比λ=0.5~2.5 时,各个算例的弯剪相关关系如图10 所示,其中,极限抗剪承载力Vu取Vλ=0.5,极限弯矩Mu取Mλ=2.5。图10 中,实线为本文建议的装配式双拼槽钢混凝土组合梁弯矩-剪力相互作用曲线。
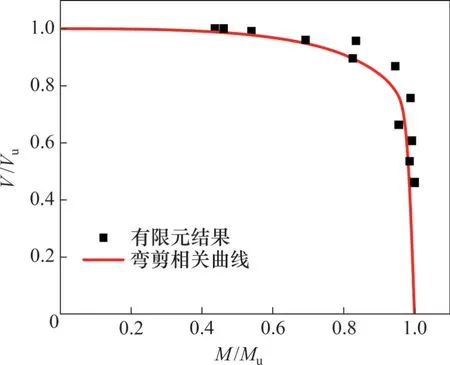
图10 弯矩-剪力相互作用曲线Fig. 10 Bending moment-shear interaction curves
根据Von Mises 强度理论分析,受弯剪作用时,钢梁腹板中存在的剪应力对截面的极限抗弯承载力产生不利影响。由图10 可见:在组合截面竖向抗剪承载力V大于Vu的70%时,组合梁的竖向剪力对其抗弯承载力的不利影响非常显著。
3.3 材料强度
以DCCB-6为基础建立有限元模型,分别采用Q235~Q420 的钢材强度、C30~C60 的混凝土强度进行模拟分析。结果表明:1) 钢梁屈服强度变化对组合梁的抗剪承载力影响显著,如图11(a)所示,钢梁型号由Q235提高至Q420,组合梁抗剪承载力提高56.40%;2) 混凝土强度的变化对组合梁抗剪承载力影响较小(如图11(b)所示),混凝土型号由C30提高至C60,组合梁抗剪承载力提高幅度低于4.20%。
随着乡村经济水平的不断提高,贷款需求呈现多样化趋势,因此,必须创新农村金融产品,坚持以市场为导向,提供适合乡村经济发展的信贷产品,根据土地、林地等,开发土地承包经营权贷款、宅基地使用权贷款与林权抵押贷款以及信贷+保险方面的贷款产品,满足农村新型经济组织多方面的金融需求,农村金融产品可以从抵押形式、担保机制、风险机制、信用增级和支付结算等方面进行创新。

图11 材料强度和截面尺寸对组合梁承载力的影响Fig. 11 Influence of material strength and section size on composite beam bearing capacity
3.4 截面尺寸
分别对DCCB-6数值模型的钢梁腹板高度与厚度和混凝土板宽度与厚度进行分析。钢梁和混凝土板截面尺寸变化对抗剪承载力的影响规律如图11(c)~(f)所示。由图11(c)~(f)可知:
1) 钢梁腹板高度与厚度变化对组合梁承载力影响较大。当腹板hw×tw从15 mm×400 mm 增大至30 mm×400 mm 时,组合梁承载力提高30.17%;当腹板hw×tw从25 mm×280 mm 增大至25 mm×400 mm时,组合梁承载力提高63.88%。
2) 混凝土板尺寸变化对组合梁承载力影响较小。当混凝土板宽由600 mm增大到1 200 mm,剪跨比λ为0.20、1.25 和2.50 时,组合梁抗剪承载力分别提高了3.98%、4.55%和6.41%;当混凝土板厚度从80 mm 增大到120 mm,剪跨比λ为0.20、1.25 和2.50 时,组合梁抗剪承载力分别提高了4.06%、3.90%和2.53%。
3) 随着剪跨比增大,板宽变化对抗剪承载力的影响更加显著,板高变化对抗剪承载力的影响程度降低。当构件DCCB-1 与DCCB-4 的剪跨比λ=4.69,板宽从600 mm增大至1 200 mm时,组合梁抗剪承载力提高了25.14%。
4 组合梁计算公式
由于组合梁抗剪机理复杂,难以获得可靠的理论公式。本文在对试验结果分析的基础上,通过有限元分析方法研究影响抗剪承载力的主要因素,然后提出经验回归公式。
4.1 抗剪承担比例
不同剪跨比下纯钢梁和组合梁的抗剪承载力对比见图12。从图12 可见:与纯钢梁相比,组合梁的抗剪承载力提升了14.23%~25.68%,随着剪跨比的减小而增大;受组合作用的影响,钢梁的抗剪承载力较纯钢梁的抗剪承载力略微增加;当剪跨比减小时,其抗剪承载力显著降低。组合梁抗剪承担比例见图13。从图13 可知:在剪跨比较小时,混凝土板的抗剪承担比例达到了42.66%,其对于组合梁的抗剪贡献显著,抗剪作用不容忽视。

图12 纯钢梁和组合梁的抗剪承载力对比Fig. 12 Comparison of shear capacity between pure steel beam and composite beam
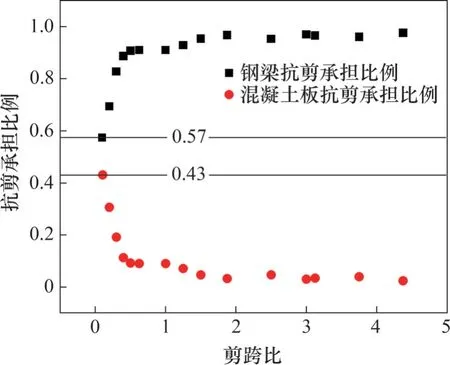
图13 组合梁抗剪承担比例Fig. 13 Shear bearing ratio of composite beams
双拼槽钢-混凝土组合梁的抗剪承载力Vu可由钢梁的抗剪承载力Vs与混凝土板抗剪承载力Vc叠加得到:
4.2 抗剪承载力公式
4.2.1 混凝土板
对于组合梁混凝土板抗剪承载力的计算,LIANG等[21]采用Vc=k1fc1/3Ace的计算模型,其中,Ace为混凝土板有效抗剪面积,Ace=(bf+hc)hc,朱劲松等[10,17,22]考虑剪跨比的影响,采用Vc=k1fck2bchc/(k3+λ)的计算模型;聂建国等[13-14]考虑混凝土板宽厚比和钢梁剪跨比的影响,采用Vc=m=(bc/hc)(hc/hs)3的计算模型。本文通过研究发现,混凝土板宽度和厚度对该组合梁抗剪承载力的影响程度随剪跨比λ变化,而变化其关系式[23]为
式中:α=hc/bc。对式(9)进行拟合,得出混凝土翼板抗剪承载力计算式(10),混凝土板抗剪承载力-剪跨比关系曲线如图14 所示,相关系数R2=0.88,相关性良好。
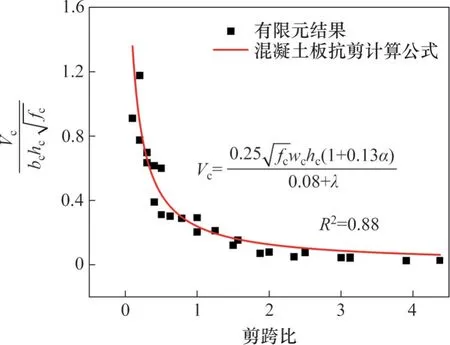
图14 混凝土板抗剪承载力-剪跨比曲线Fig. 14 Shear load-shear span ratio curve of concrete slab
4.2.2 钢梁
对于组合梁钢梁抗剪承载力Vs的计算,朱劲松等[10,13-14,21-23]采用Vs=hwtwfv的模型、丁发兴等[17]发现剪跨比对钢梁抗剪贡献的影响显著,采用了Vs=k1hwtwfv/(k2λ)的模型。本文基于试验和有限元分析结果,采用Vs=ϕ(λ)hwtwfv的计算模型得出双拼槽钢-混凝土组合梁的钢梁抗剪承载力计算式(11),钢梁抗剪承载力-剪跨比关系曲线如图15所示。
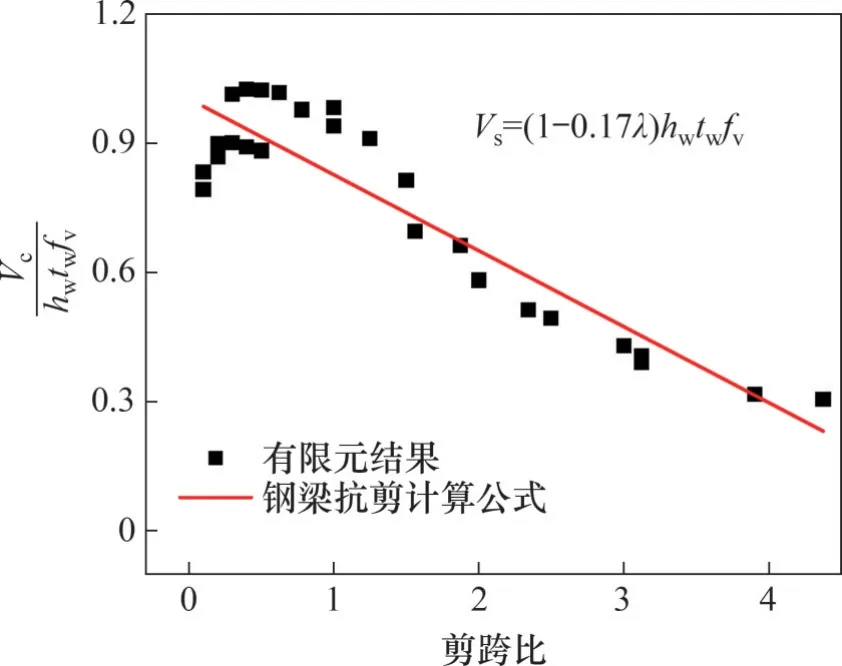
图15 钢梁抗剪承载力-剪跨比关系曲线Fig. 15 Shear load-span ratio curve of steel beam
4.2.3 组合梁抗剪承载力计算公式
通过回归得到混凝土板和钢梁的抗剪承载力与剪跨比关系曲线,整合式(8)~(11),可得双拼槽钢-混凝土组合梁抗剪承载力公式为
式中:α为组合梁混凝土板的高宽比,α=hc/bc。
4.3 公式验证
采用本文建立的63组有限元模型计算结果和试验结果,与式(12)的计算结果、GB 50017—2017[24]中的结果、文献[17]建议的组合梁抗剪极限承载力计算结果进行比较,如图16 所示。从图16 可见:相比GB 50017—2017 和文献[17]中的结果,本文建议的组合梁抗剪承载力公式具有较高的精度,与有限元计算结果、试验结果都较吻合,且相比文献[17]中的经验公式计算结果,对于极限抗剪承载力较高的组合梁,采用式(12)得出的计算结果是偏于安全的。采用式(12)所得结果、GB 50017—2017中结果、文献[17]中结果与有限元计算值以及试验值的比值均值和离散系数见表4。从表4可见:采用式(12)所得计算结果与有限元计算结果、试验结果都非常接近,比值均值为1.07,离散系数为0.15,准确地预测了不同破坏模式下的组合梁抗剪承载力,较其他公式所得结果精度更高,适用性好。

表4 试验结果和有限元计算结果与不同公式计算结果比较Table 4 Comparison of test results and finite element calculation results with those calculated by different formulas
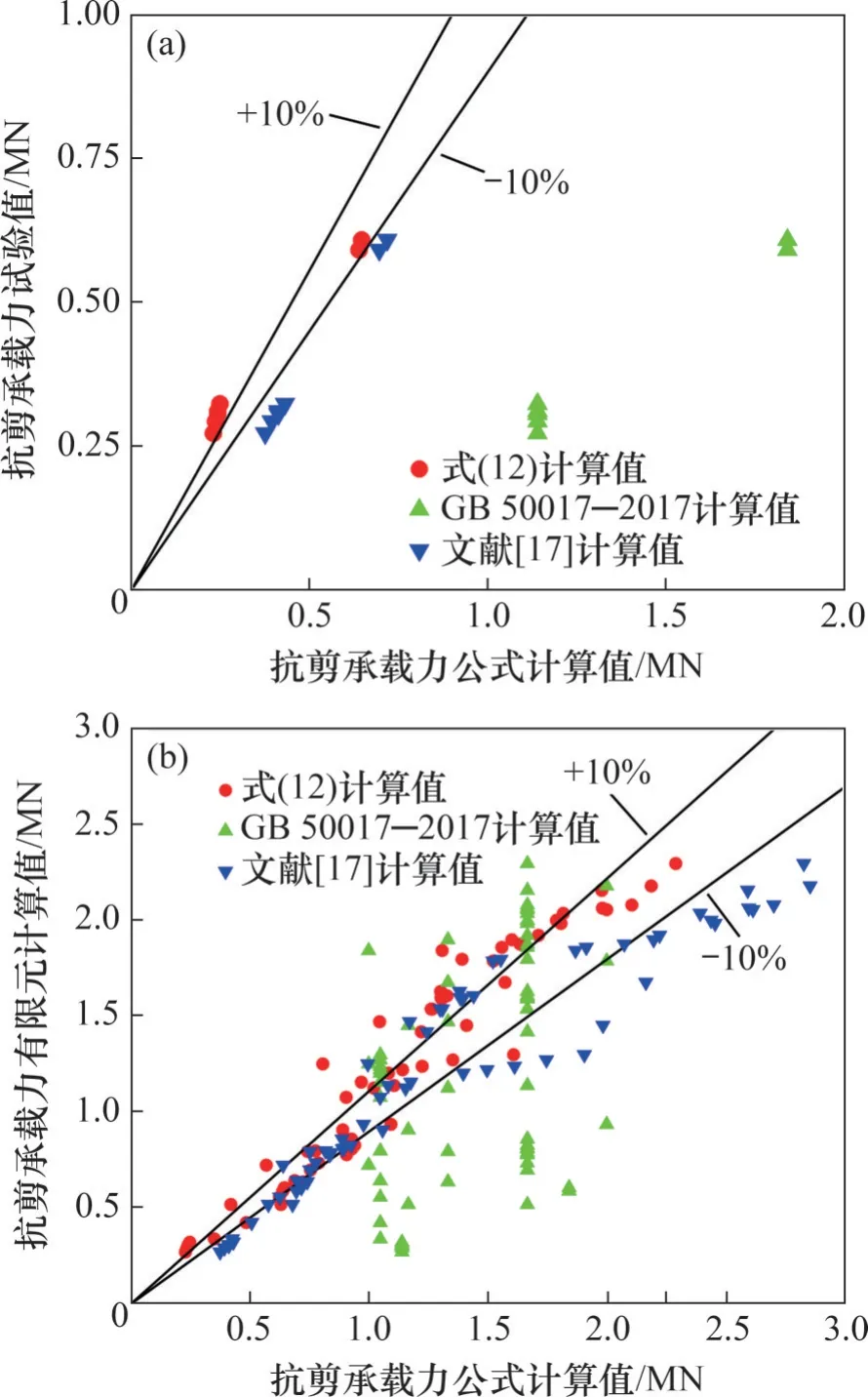
图16 组合梁抗剪承载力试验值和有限元计算值与公式计算值比较结果Fig. 16 Comparison of test shear capacity of composite beam and finite element calculated value with formula calculated value
5 结论
1) 双拼槽钢-混凝土组合梁的2 个预制模块协同工作良好。与传统的工字形钢梁组合梁相比,混凝土板抗剪承担比例更小,该组合梁具有更优异的抗剪性能。
2) 确定了双拼槽钢-混凝土组合梁剪切破坏、弯剪破坏与弯曲破坏的界限剪跨比λ分别为0.5 和2.5;得出了组合梁弯剪破坏状态时的弯剪相互作用曲线。
3) 组合梁抗剪由混凝土板和钢梁共同承担,混凝土板抗剪贡献为3.42%~42.66%,混凝土板抗剪贡献随剪跨比减小而增大。
4) 提出了考虑混凝土板的抗剪贡献、剪跨比对抗剪分担比例影响的组合梁极限抗剪承载力计算公式。相比规范中的组合梁抗剪承载力计算公式和其他学者建议的组合梁抗剪承载力计算公式,本文提出的计算公式所得结果计算精度较高,可为相关组合梁结构设计和建造提供参考。
