基于带宽调整的两种混合载波跟踪环路研究

张红斌，李彤彤，王晓君，刘昊昱

(1.河北科技大学 信息科学与工程学院，河北 石家庄 050018；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

锁频环和锁相环是常用的载波环[1-2],锁频环的跟踪动态范围较大,但精度不高;锁相环精度高,但跟踪动态范围较小。目前研究较多的为二阶锁频环辅助三阶锁相环[3-5],在增大跟踪动态范围的同时提高了环路的跟踪精度[6-7]。在应对频率二次斜升激励时,三阶锁相环存在非零稳态误差值,而四阶锁相环稳态误差为零,本文选用四阶锁相环进行研究。

当本地复现载波频率与实际载波频率频差较大时[8],单一的锁频环辅助锁相环将面临失锁,此时可以依据对频率判决因子的判断先通过四相鉴频器进行频率牵引[9-10],而后用载波环路进行跟踪。

面对高动态环境中的加加速度动态[11],本文采用三阶锁频环辅助四阶锁相环载波跟踪环路,通过频率判决因子完成与四相鉴频器相互切换的2种混合载波跟踪算法。依据动态跟踪误差求解出环路带宽[12],通过相位判决因子完成载波环带宽的动态调整。仿真比较跟踪初始多普勒较大或环路稳定跟踪后有较大动态变化时,基于带宽调整的2种混合载波跟踪环路与三阶锁频环辅助四阶锁相环载波跟踪环路这2种环路恢复电文信息情况和不同载噪比下的跟踪载波相位误差。

1 三阶锁频环辅助四阶锁相环载波跟踪环路设计

1.1 三阶锁频环辅助四阶锁相环滤波器设计

图1为三阶锁频环辅助四阶锁相环的环路滤波器结构。

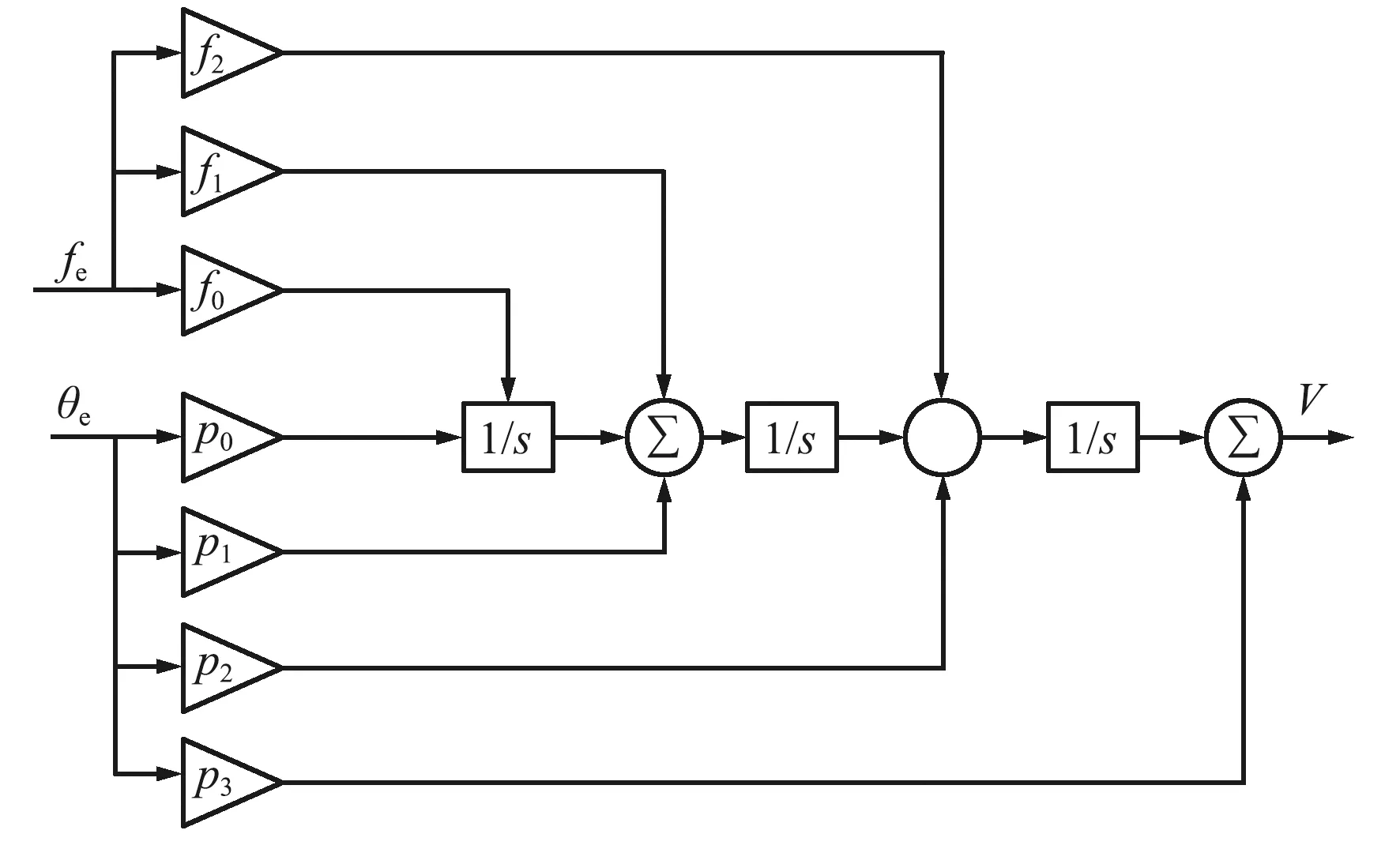
图1 三阶锁频环辅助四阶锁相环滤波器结构Fig.1 Structure diagram of fourth-order PLL filter assisted by third-order frequency-locked loop

滤波器传递函数为[13]:

(1)

式中:p0、p1、p2、p3对应图1中的环路参数。

通过对理想二阶滤波器进行级联构造了三阶滤波器[6],其传递函数为:

(2)

式中:τ1=R1C,τ2=R2C。

式(1)与式(2)比较,得:

(3)

由文献[14]可知:

(4)

则,四阶锁相环的参数为:

设定a4=4.242,b4=5.998,c4=2.827[15]。

同理可得三阶锁频环的参数f0、f1、f2为:

(6)

环路的传递函数H(s)和误差传递函数He(s)为[16]:

式中:K=K0K1为环路增益,取K=1。

将式(1)代入式(7)和式(8),得:

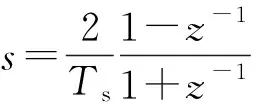
(11)

式中:

(12)

数控振荡器的传递函数V(z)为:

(13)

数字式锁相环系统函数H(z)为:

(14)

四阶锁相环的系统函数和误差传递函数为:

1.2 稳态误差

由式(15)和式(16)可推出N阶锁相环系统的传递函数和误差传递函数为:

相位按照时间的三次方增长称为频率二次斜升激励[17]。发生在零时刻的频率二次斜升激励θi(n)为:

(19)

z变换后:

(20)

根据终值定理和式(18),可知N阶锁相环在输入频率二次斜升激励时误差信号θe(n)的稳态终值:

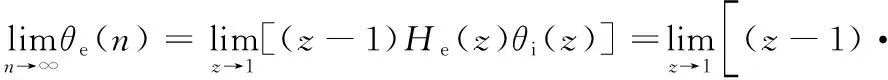
(21)

可得:

(22)

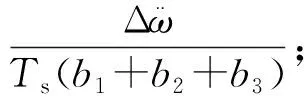
1.3 环路带宽

相位抖动和动态应力误差构成锁相环跟踪误差,相位抖动由热噪声、阿仑偏差和机械颤动组成[18]。外界环境和载波频率决定机械颤动误差σv,与环路参数无关,在此不做讨论。

锁相环跟踪误差为:

式中:T为积分时间,BL为环路带宽,C/N0为载噪比,σA=1×10-9,fL为载波频率。

(24)

频率抖动和动态应力误差构成锁频环跟踪误差,热噪声造成的频率抖动,机械颤动和艾兰方差引起的频率抖动量较小,此处忽略不计[7]。

锁频环跟踪误差为[17]:

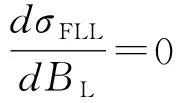
(26)

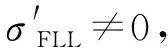
2 四相鉴频器原理

输入的中频信号通过下变频和相关积分后的结果可表示为[17]:

(27)

相关器进行1 ms的相关运算,由于在一个导航数据内进行运算,于是取D(n)=1,根据式(27)可得:

|Ip(n)|-|Qp(n)|=aR[τn]·sinc(fe(n)T)·

(|cosφe(n)|-|sinφe(n)|)。

(28)

捕获后的码相位估计误差在一个码片内,因此R[τn]>0,说明|Ip(n)|-|Qp(n)|和|cosφe(n)|-|sinφe(n)|符号相同,将载波频率误差分割为4个区间。定义Δf(n)为设四相鉴频器校正量,Δf(n)可表示为:

当|Ip(n)|≥|Qp(n)|时,有:

Δf(n)=sign[Ip(n)]·[Qp(n)-Qp(n-1)],

(29)

当|Ip(n)|<|Qp(n)|时,有:

Δf(n)=-sign[Qp(n)]·[Ip(n)-Ip(n-1)],

(30)

噪声不计,由式(27)可得:

(31)

令[15]:

dot(n)=I(n-1)I(n)+Q(n-1)Q(n)=

D(n-1)D(n)cos(φe(n)-φe(n-1)),

(32)

cross(n)=I(n-1)Q(n)-Q(n-1)I(n)=

D(n-1)D(n)sin(φe(n)-φe(n-1))。

(33)

若在一个数据上进行采样,当频率锁定时,D(n-1)D(n)=1,φe(n)-φe(n-1)→0,则:

sign[dot(n)]·cross(n)=

sign(D(n)D(n-1)cos(φe(n)-φe(n-1))·

D(n)D(n-1)sin(φe(n)-φe(n-1))=

sign(D(n)D(n-1))·

D(n)D(n-1)sin(φe(n)-φe(n-1))=

|D(n)D(n-1)|sin(φe(n)-φe(n-1))=

φe(n)-φe(n-1)。

(34)

因此,四相鉴频器的校正量Δf(n)取Δf(n)=sign(dot(n))cross(n)。

3 基于带宽调整的两种混合载波跟踪环路

3.1 判决因子的选取

由式(32)可知,当φe(n)-φe(n-1)趋于零时,此时dot(n)趋于1,表示频率锁定,令φf=dot(n),选取φf作为频率判决因子。当跟踪初始多普勒较大时,频差较大,这将远远超出锁相环的线性工作范围。为了解决此问题,当频率判决因子大于0.9时,载波跟踪环路工作在线性工作范围较大的四相鉴频器。

鉴相采用二象限反正切函数[19]:

(35)

将式(27)代入式(35),得:

(36)

由式(27)得知[20]:

(37)

cos[2φe(n)]值可以反映当前环路的相位误差,当相位误差φe(n)趋于零时,cos[2φe(n)]趋于1,认为相位锁定。令φp=cos[2φe(n)],选取φp作为相位判决因子[10]。当φp<0.5时,依据φp对环路带宽进行动态调整。

3.2 基于带宽调整的2种混合载波跟踪环路的构建

中频信号完成积分累加后得到IP和QP,一方面经鉴别器得到频率误差fe和相位误差θe,另一方面计算出频率判决因子和相位判决因子。当跟踪频率判决因子φf<0.9时,采用四相鉴频器进行频率牵引并更新载波NCO,调整载波频率;当φf>0.9时,采用三阶锁频环辅助四阶锁相环载波跟踪环路,并根据相位判决因子φp对载波环带宽进行实时调整。当判决因子φp≥0.5时,选取通过动态跟踪误差求解出的载波环带宽BFL和BPL;当判决因子φp<0.5时,在BFL和BPL基础上加上(1-φ)BFL和(1-φ)BPL对载波环带宽进行实时调整,更新载波NCO,调整载波频率,保持对信号的跟踪锁定。基于带宽调整的2种混合载波跟踪环路阶结构如图2所示。

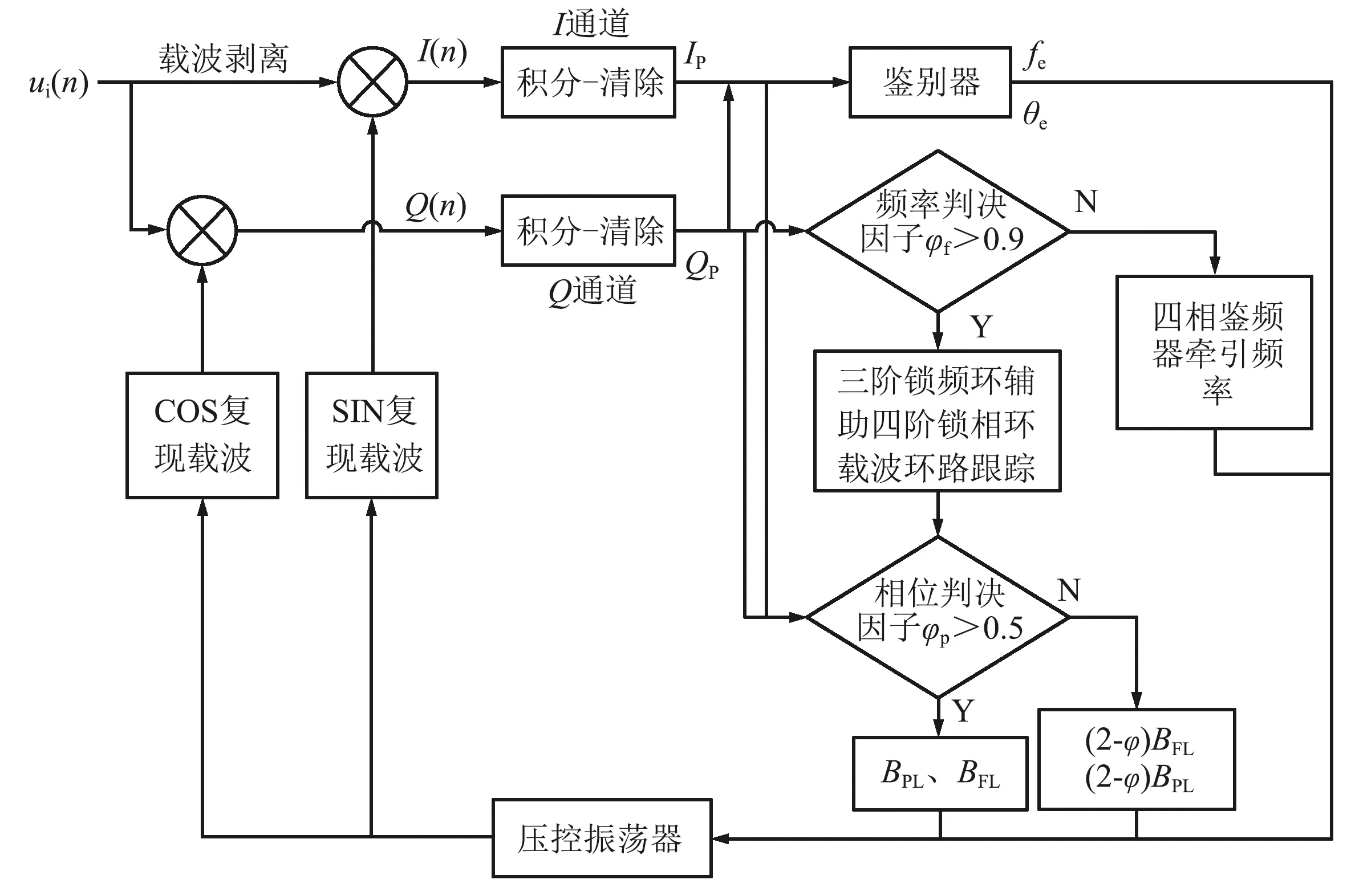
图2 基于带宽调整的2种混合载波跟踪环路结构Fig.2 Structure diagram of two kinds of hybrid carrier tracking loops based on bandwidth adjustment

4 仿真

中频频率为46.098 MHz,采样频率为62 MHz,仿真数据时间为1 s、一个电文时长设定为0.02 s,仿真数据时间、一个电文时长结合采样频率可计算出一个电文的采样点数和总采样点数。通过总采样点数除以一个电文的采样点数的商对2取余生成一组±1交替的电文。

积分时间T取1 ms,由式(24)可知锁相环带宽BPL为45.9 Hz,锁频环带宽BFL取10 Hz。高动态环境为5 000/150g/120g、载噪比为42 dB/Hz时,仿真分析进入跟踪初始多普勒分别为0、300 Hz两种情况下环路剥离±1交替的电文情况;跟踪初始多普勒为0时,比较2种环路稳定跟踪后在原动态上加入25/20g/20g动态时环路跟踪和剥离±1交替的电文情况。

高动态环境为5 000/150g/120g、载噪比为 42 dB/Hz、跟踪初始多普勒为0时,2种环路I、Q支路跟踪结果如图3和图4所示。观察I支路跟踪结果可知,2种环路均可准确无误地剥离出±1交替的电文。

高动态环境为5 000/150g/120g、载噪比为 42 dB/Hz、跟踪初始多普勒为0时,2种环路稳定跟踪后在原动态基础上加入25/20g/20g动态2种跟踪环路的I、Q支路跟踪结果如图5和图6所示。观察I支路可知,加入25/20g/20g动态后,通过四相鉴频器对频率牵引的辅助,基于变带宽的2种混合载波跟踪环路可以重新实现稳定跟踪,且准确剥离出±1交替的电文;三阶锁频环辅助四阶锁相环载波跟踪环路失锁。

图5 高动态环境为5 000/150g/120g、载噪比取42 dB/Hz、跟踪初始多普勒为0时,环路稳定跟踪加入25/20g/20g动态后基于变带宽的2种混合载波跟踪环路I、Q支路跟踪结果 Fig.5 Tracking results of I and Q branches of two kinds of mixed carrier tracking loops based on variable bandwidth after adding 25/20g/20g dynamics to the loop stability tracking when the high dynamic environment is 5 000/150g/120g,the carrier-to-noise ratio is 42 dB/Hz, and the initial tracking doppler is 0

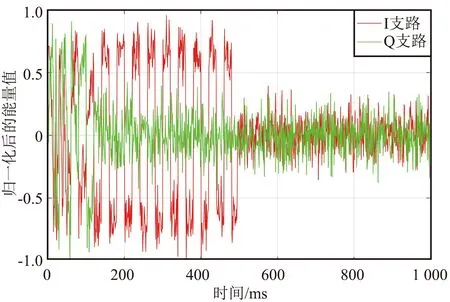
图6 高动态环境为5 000/150g/120g、载噪比取42 dB/Hz、跟踪初始多普勒为0时,环路稳定跟踪加入25/20g/20g动态后三辅四载波跟踪环路I、Q支路跟踪结果Fig.6 Tracking results of I and Q branches of the three assisted four-carrier tracking loop with 25/20g/20g dynamic are added to the loop stability tracking when the high dynamic environment is 5 000/150g/120g,the carrier-to-noise ratio is 42 dB/Hz,and the initial tracking doppler is 0

高动态环境为5 000/150g/120g、载噪比取 42 dB/Hz、跟踪初始多普勒为300 Hz时,两环路I、Q支路跟踪结果如图7和图8所示。由于进入跟踪时的初始多普勒较大,导致三阶锁频环辅助四阶锁相环载波跟踪环路无法剥离出±1交替的电文且Q支路的噪声能量也很大;2种混合载波跟踪环路在应对进入跟踪时的初始多普勒较大的情况,首先采用四相鉴频器将多普勒牵引到锁相环的线性工作范围(一般不超过100 Hz),再通过载波环进行跟踪,最终可剥离出±1交替的电文。

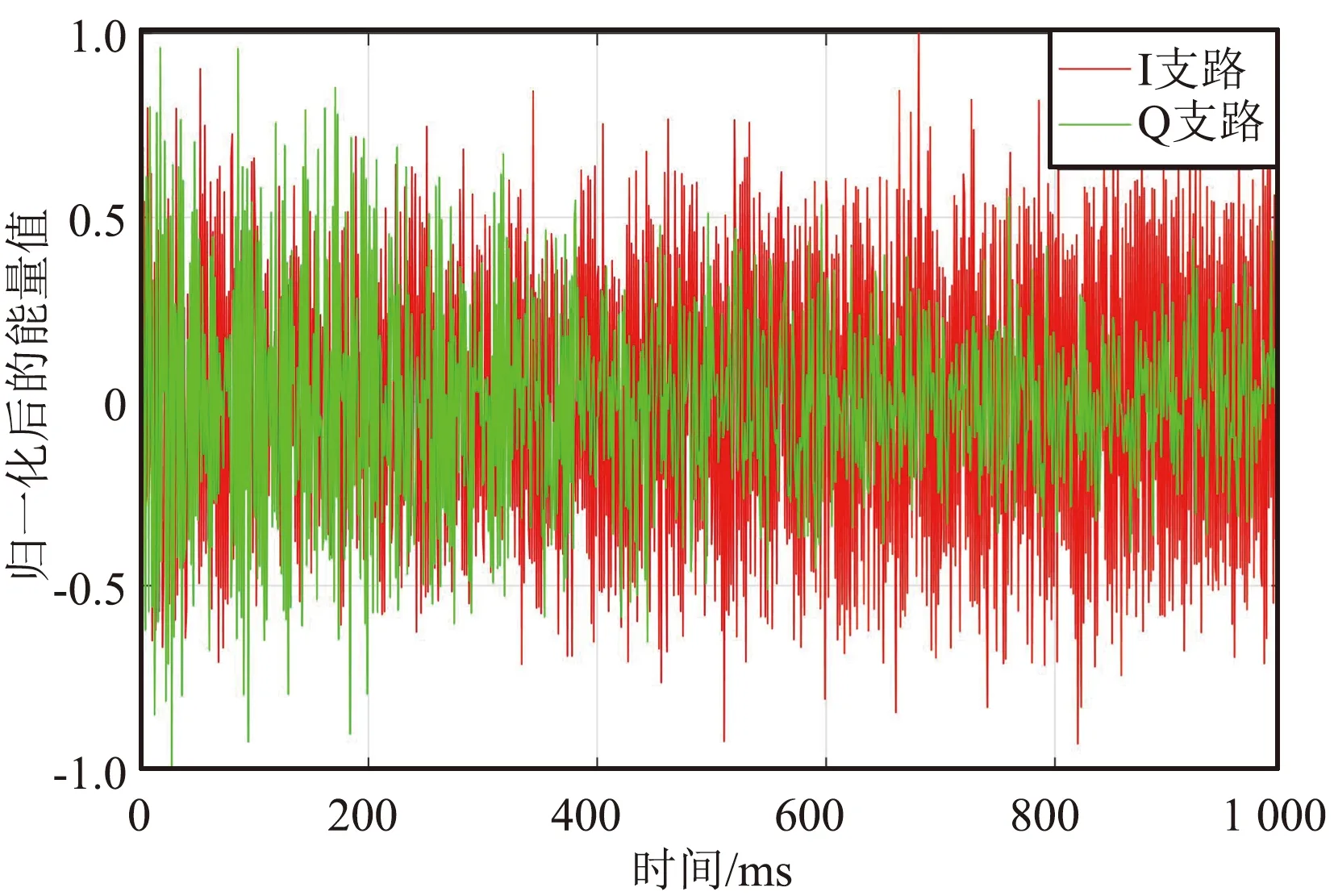
图8 高动态环境为5 000/150g/120g、载噪比取42 dB/Hz时、跟踪初始多普勒为300 Hz时,三辅四载波跟踪环路I、Q支路跟踪结果Fig.8 Tracking results of I and Q branches of the three assisted four-carrier tracking loop when the high dynamic environment is 5 000/150g/120g,the carrier- to-noise ratio is 42 dB/Hz, and the initial tracking doppler is 300 Hz

图9为不同载噪比下的2种环路跟踪相位误差方差比较图,信号载噪比越大跟踪精度越高。当信号比较强,载噪比大于44 dB/Hz时,2种环路的跟踪相位误差方差大致一样;载噪比为38～44 dB/Hz时,2种环路的跟踪相位误差方差虽存在差异,但相差不大;当载噪比小于38 dB/Hz,信号较弱时,显而易见,基于变带宽的2种混合载波跟踪环路的跟踪相位误差方差更小,相差明显,当信号强度较弱时,可以选取基于带宽调整的2种混合载波跟踪环路,跟踪载波相位误差相对更小,跟踪精度更高。

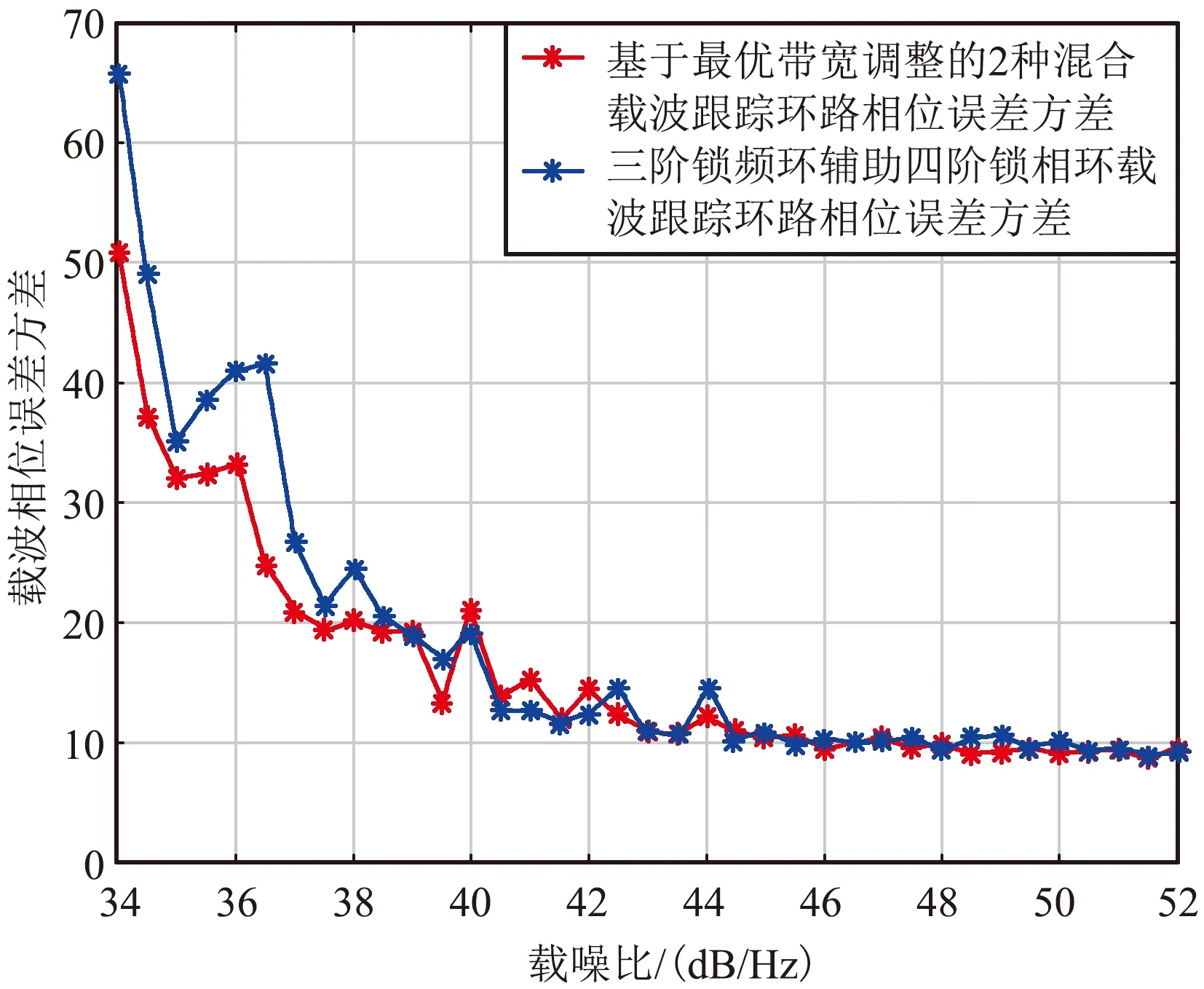
图9 不同载噪比下2种环路的跟踪相位误差方差值比较Fig.9 Comparison of tracking phase error variance of two loops under different carrier-to-noise ratios

5 结束语

针对目前研究的三阶锁相环存在稳态误差的情况,本文构建了三阶锁频环辅助四阶锁相环的跟踪环路,通过对频率判决因子φf的判断实现四相鉴频器和三阶锁频环辅助四阶锁相环2种载波跟踪环路的相互切换,依据判决因子φp对环路带宽进行动态调整。仿真结果表明,在5 000/150g/120g的动态下,载噪比取42 dB/Hz,跟踪初始多普勒较大或稳定跟踪后有较大动态变化时,基于带宽调整的2种混合载波跟踪环路均可恢复出电文信息,而单一的三阶锁频环辅助四阶锁相环不可以,且低载噪比时基于带宽调整的2种混合载波跟踪环路跟踪相位误差方差更小、精度更高。因此,当载噪比较低、环境的动态不稳定或开始时进入环路的多普勒较大时可选用基于带宽调整的2种混合载波跟踪环路。