超宽带信号数字预失真时延补偿算法
2023-10-12赵林军张海林
赵林军,张海林,王 方
(1.陕西理工大学 物理与电信工程学院,陕西 汉中 723001;2.西安电子科技大学 通信工程学院,陕西 西安 710071;3.中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
数字预失真(Digital Pre-Distortion,DPD)是改善功率放大器(Power Amplifier,PA)输出特性的一种技术[1-2]。按其工作的频率不同,可将DPD分为射频预失真技术[3]与基带预失真技术[4]。其中,基带DPD以结构多变[5]等优点得到广泛应用。
众所周知,DPD的2路激励信号之间存在的时延差[6-7]是影响DPD算法稳定性与校正后PA线性度的主要因素。因此,DPD系统中设有信号时延估计算法与信号时延补偿处理电路[8]。
目前,在基带DPD系统中用于激励信号间时延估计的算法主要有迭代法[4]、延时锁定环法[9]、幅度相关函数法[10-11]、基于小波分析时延估计算法[12]、基于搜索法时延估计算法[13-14]与互谱相位法[15]等。其中,文献[4]研究了基于时域迭代的信号时延估计方法,该方法所需运算大,易引起收敛问题,且算法的实时性差。文献[9]论述的延时锁定环算法需通过改变系统的采样时钟实现信号的时域对齐,使得DPD的信号时延补偿电路比较复杂。文献[10-11]基于相关函数方法研究了DPD系统中的信号时延问题,通过对PA反馈信号高倍插值并抽取,构成多路并行信号,再由这些并行信号与DPD的另一路输入信号互相关,通过搜索多路互相关函数的极大值选取相对时延最小的一路抽取后信号作为时域补偿信号。显然,该算法也涉及大量运算,且并未解决DPD系统中信号间可能存在的分数时延模糊问题(由于信号离散化,DPD系统中存在信号时延小于一个采样间隔的问题)。文献[12]基于小波分析法研究了DPD系统中信号时延问题,在其相关算法中由于需要对DPD系统的输入信号进行多次小波变换,因此相关算法的时效性使得其在实际的DPD系统中难以推广应用。文献[13-14]研究了并行搜索时延估计算法,电路复杂、计算量大。文献[15]研究了互谱相位时延估计方法,该方法的时延估计抗噪性能优越,但计算复杂。
在基带DPD系统中,用于激励信号的时域对齐处理方法主要有:重采样滤波器[13]和多项式近似插值法[14]等。其中,重采样滤波器或多项式近似插值的精度受到存贮系数的查找表(Look-up Table,LUT)单元数量或迭代运算的限制[16-18],普遍存在计算量大、计算误差累计等问题。
近年来,DPD中有关信号时延补偿的研究成果不断出现。文献[19]基于最小二乘算法研究了DPD多项式系数的动态修正问题。文献[20]基于收缩映射定理研究了多级级联解决DPD的信号对齐问题。文献[21]基于多项式近似插值法研究了其信号时域补偿问题。文献[22]基于神经网络理论研究了深度学习DPD的系统的实现。这些算法同样存在着运算的速度或精度问题。
综上所述,由于面向未来超宽带信号的预失真需要,继续探究DPD中信号时延补偿方法仍具有现实意义。文中以DPD两路激励信号的整数倍采样间隔时延估计使用的幅度互相关函数为基础,结合最优化插值理论,提出了一种二次线性拟合分数倍采样间隔时延估计,在此基础上,研究了带有信号时延参数的“插值”滤波器实现DPD两路激励信号的时域补偿问题。
对所提算法进行了数学建模及数值分析。由给出的分数倍采样间隔时延估计数值结果看,当DPD两路激励信号间的倍采样间隔时延在 [-Ts/2,+Ts/2] (Ts为DPD中的信号采样间隔)时,使用所研究的二次线性拟合分数倍采样间隔时延估计算法可以获得的时延估计值与分数时延的理论值之间的最大差值不大于0.03Ts;由时域补偿算法对DPD性能的影响结果不难发现,倘若使用本文研究的信号时域补偿算法可以获得不低于并行搜索信号时域补偿算法所实现的DPD性能。在离散域中,由于研究的信号补偿算法无需对DPD激励信号进行倍插与抽取,且插值滤波器的系数也无需迭代,因此该时域补偿算法的运算量小,便于FPGA实现。
1 算法理论
为了便于论述文中所提时延估计算法与信号插值对齐算法的特点,采用如图1所示的基带DPD直接学习模式结构实现PA线性化校正。其中,数模转换器(Digital to Analog Converter,DAC)与模数转换器(Analog to Digital Converter,ADC)的时钟速率相同,设为fs=1/Ts;“前插”滤波器(Forward Interpolation Filter,FIR)根据回路时延估计器(Time Delay Estimator,TDE)的输出对y(n)进行“前插”处理,实现信号的对齐。在匹配条件下,图1所示的系统噪声仅考虑高斯白噪声,LO为本地振荡器,G为信号缩减因子。
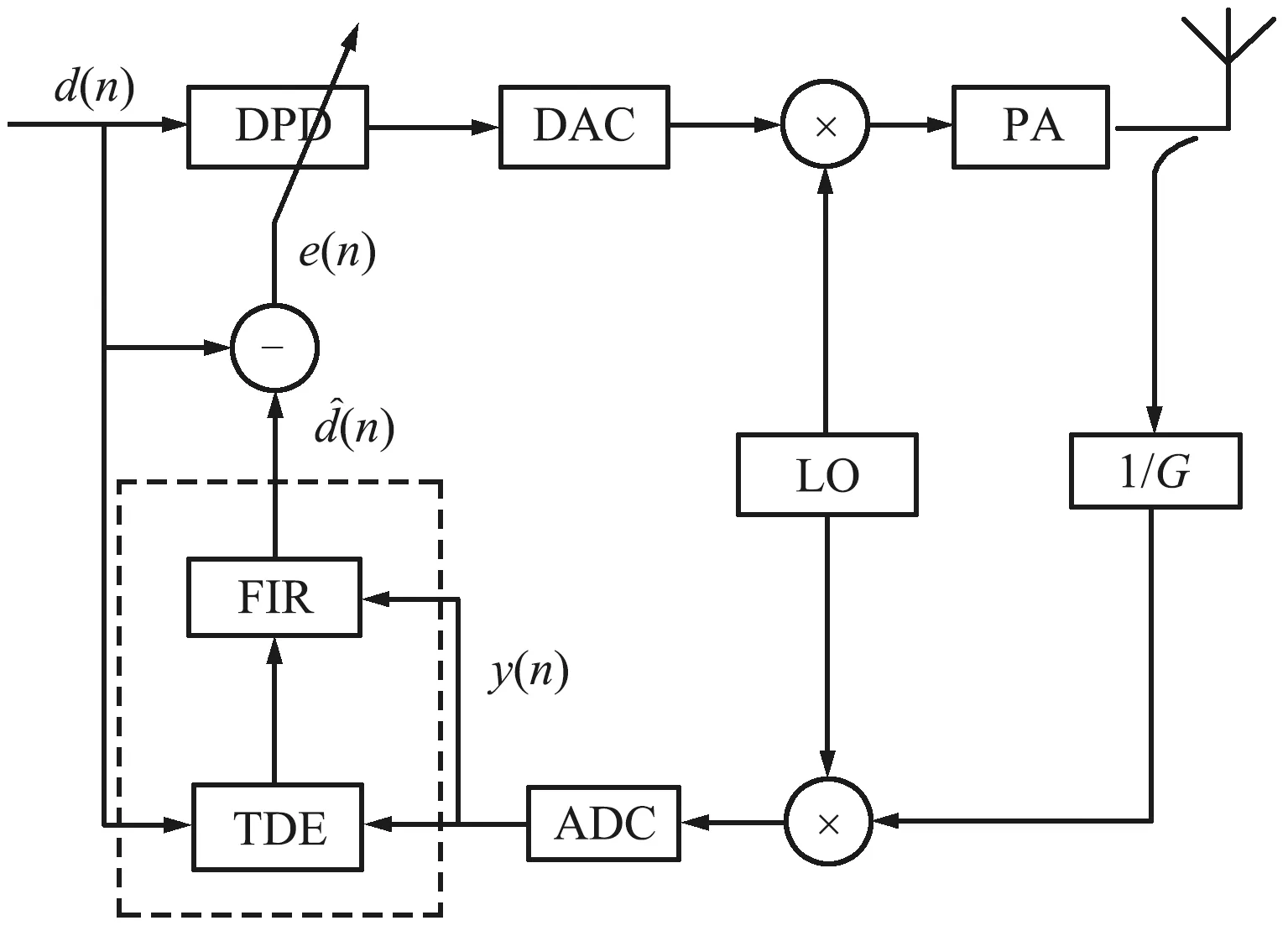
图1 基带DPD直接学习模式结构Fig.1 Structure of baseband-based DPD direct learning
1.1 分数时延估计
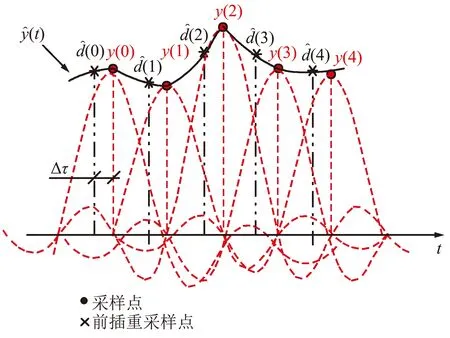
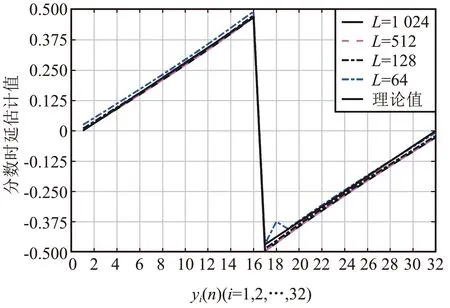
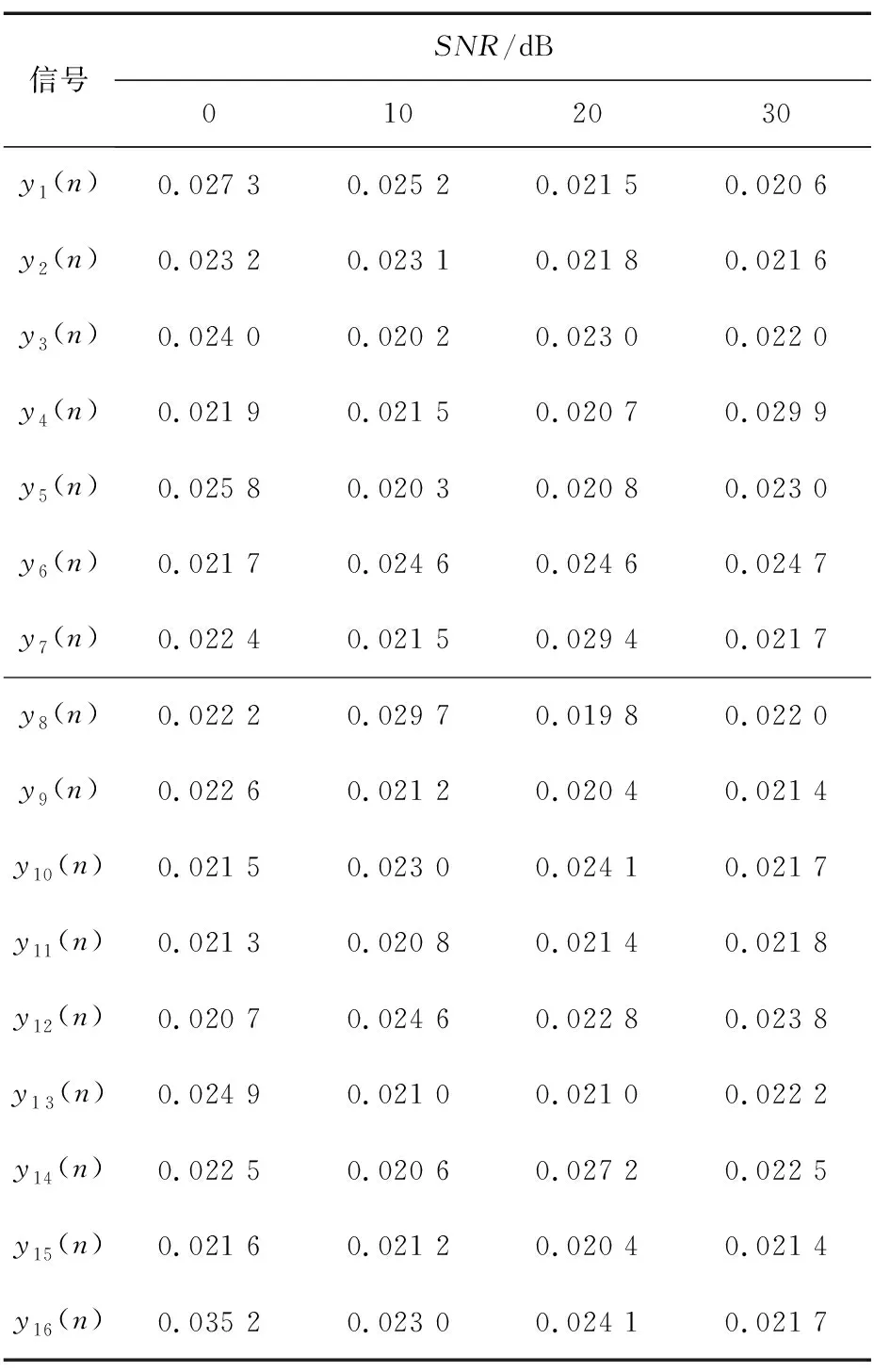
连续时间域两信号的幅度互相关函数r(t)与采样后的离散时间域对应的幅度互相关函数r(n)的包络关系如图2所示。不难发现,连续时间域两信号的时延与其离散化后的估计时延值一般存在Δτ偏差,主要是采样脉冲相位的不确定性造成的,学界将其称为采样间隔时延模糊问题。因|Δτ| 图2 信号离散化导致时延模糊示意Fig.2 Time delay fuzziness due to signal discretization 图2中,r1、r2与r3为离散幅度互相关函数r(n)的3个极大值,τ1、τ2与τ3为其在时间轴τ上的对应坐标。若以τ2为时间原点,当r1>r3时,Δτ<0;当r1 如图1所示,若信号d(n)与信号y(n)之间存在总时延γ,可根据离散信号处理理论,对信号y(n)进行“超前”插值处理,以实现与DPD另一激励信号d(n)的时域对齐。 信号y(n)时域“超前”插值处理的理论如下。 (1) (2) 图1中,信号d(n)与信号y(n)之间存在以采样间隔为单位的整数时延τ2和分数时延Δτ。 2.1.1 整数时延估计 采用幅度互相关函数实现整数时延τ2估计,其步骤如下:同时截取信号y(n)与信号d(n)各N点,分别记为dN(n)与yN(n)。做信号dN(n)与信号yN(n)的幅度互相关运算: r2N-1(τ)=dN(n)*yN(-n),τ=0,1,…,2N-1。 (3) 当dN(n)与yN(n)间无相对时延,则图2中曲线r(n)与r(t)的峰值对应的时间是重合的,有τ2=N;当dN(n)与yN(n)间存在相对时延,则τ2≠N,此时信号dN(n)与yN(n)间的整数采样间隔时延为: T=(τ2-N)·Ts。 (4) 2.1.2 分数时延估计 式(3)所得离散幅度互相关函数r2N-1(τ)的2个次大值r1与r3为: (5) 由文献[23]中的“三点二次”插值最优化算法,可取图2中的曲线r(n)关于时间轴τ镜像,如图3所示。于是,图3中的点(τ1,-r1)、(τ2,-r2)、(τ3,-r3)满足“三点等距”二次插值“中间小,两头大”的条件,于是有: (6) 显然,当r1>r3时,Δτ<0,意味着信号离散使得离散互相关函数的峰值落在了连续化相关函数峰值的右侧;当Δτ>0时,r1 2.1.3 时延估计算法实现 DPD系统中,d(n)与y(n)的时延估计算法实现步骤如下: ① 同时截取d(n)与y(n)各N(N=2m,m∈Z+),记为dN(n)与yN(n); ② 采用圆周相关方法计算dN(n)与yN(n)的互相关函数r2N-1(n); ③ 根据相关函数r2N-1(n)峰值法,取|r2N-1(n)|的峰值r2与其位置号τ2,估计整数时延T; ④ 取|r2N-1(n)|的2个次大值r1、r3; ⑤ 根据式(6)估计y(n)的分数时延Δτ; ⑥d(n)与y(n)的时延估计值为T+Δτ; ⑦ 结束。 2.2.1 信号时域“前插”滤波设计 图4 信号时域插值补偿方法Fig.4 Compensation method of signal time domain interpolation Nyquist数字滤波器的单位冲激响应h(n)为: n=…,-2,-1,0,1,2,…。 (7) 实际中,Nyquist数字滤波器需由一个长为M的窗函数截取。设该窗函数为w(n),则有限长Nyquist数字滤波器的单位冲激响应为: (8) (9) 2.2.2 信号时域补偿算法实现 数字预失真系统中,y(n)与d(n)时间对齐算法的实现步骤为: ① 设定窗函数长度M与窗函数类型,计算窗函数w(n); ② 由式(8)计算hw(n); ⑤ 结束。 对图1进行建模分析。其中,PA模型选取Saleh模型[25],其参数取αA=2.158 7、βA=1.151 7、αφ=4.033、βφ=9.104;信源采用了升余弦滤波器进行符号成形后的QAM64基带信号,其中信源每符号含有8个样点,成形滤波器长为8个符号;功率放大器的记忆效应由63阶有限冲击响应数字滤波器代替,其冲击响应为: h(n)=[0.538 2,0.223 8,0.056 9,0.030 0,0.020 0, 0.015 0,0.015 0,0.010 0,0.010 0,0.010 0, 0.010 0,0.010 0,0.010 0,0.010 0,0.010 0, 0.010 0,0.010 0,0.008 0,0.008 0,0.008 0, 0.008 0,0.005 0,0.005 0,0.005 0,0.005 0, 0.003 0,0.003 0,0.003 0,0.003 0,0.002 0, 0.002 0,0.002 0,0.002 0,0.002 0,0.002 0, 0.001 0,0.001 0,0.001 0,0.001 0,0.001 0, 0.001 0,0.002 0,0.002 0,0.002 0,0.002 0, 0.002 0,0.002 0,0.002 0,0.002 0,0.001 0, 0.001 0,0.001 0,0.001 0,0.001 0,0.001 0, 0.001 0,0.001 0,0.001 0,0.001 0,0.001 0, 0.000 5,0.000 3,0.000 1]。 (10) 分数时延估计:同时截取信号d(n)与信号yi(n)(i=1,2,…,32)各L点,分别记为dL(n)与yi,L(n)(i=1,2,…,32),由信号dL(n)与信号yi,L(n)(i=1,2,…,32)对分数时延估计进行评估。 分数时延的理论值与所述的分数时延估计值对比如图5所示,给出了截取信号长L分别为64、128、512与1 024点时对分数时延的估计值分布示意。显然,当d(n)与yi(n)(i=1,2,…,15)时延相差在[0,Ts/2)时,分数时延估计值为正值;d(n)与yi(n)(i=17,18,…,32)的时延相差在(Ts/2,Ts]时,分数时延估计值为负值。 图5 分数时延估计值与理论值对比Fig.5 Fractional time delay estimation values vs. theoretical value 由图5可以看出:① 文中所述的分数时延估计算法所估值线性度良好;② 分数时延估计值随所用数据长度L的增加而更接近分数时延的理论值,当数据长L=64时,由信号d64(n)与信号y18,64(n)所估计的分数时延与理论值之间存在明显误差。为进一步阐述分数时延估计算法的性能,表1给出了时延估计值与时延理论值的具体数值对比。对比表1中yi(n)(i=1,2,…,32)行的3个数据可以发现,y17(n)行、L=512列对应的单元数据与对应的理论时延差为|0.468 8-0.496 69|Ts=0.028 1Ts,为表中数据计算对应理论时延差的最大值。可见,当数据长L不小于512点时,采用文中分数时延估计方法所得的时延估计误差不大于0.03Ts。 表1 d(n)与yi(n),i=1,2,…,32间的分数时延理论值与估计值表(Ts)Tab.1 Theoretical value of fractional time delay and its estimations between d(n) and yi(n),i=1,2,…,32 (a)时域对齐前信号实部 (d)前插滤波后信号虚部图6 时域补偿前后信号实部与虚部波形Fig.6 Real part and imaginary part of the waveform for untime domain compensation vs. time domain compensation 仿真选用文献[26]给出的Hammerstein模型作为如图1所示的DPD模型。其中,Hammerstein模型中的无记忆非线性子系为一个具有128个抽头有限冲击响应数字滤波器结构,该滤波器的系数根据图1中的信号d(n)与e(n)由最小均方(Least Mean Square,LMS)算法计算提供。信号d(n)的调制方式为256个子载波的64QAM OFDM,每OFDM符号2 048点,共5个OFDM符号数据长,即10 240个数据作为LMS算法的训练数据。 借助通信系统中用于衡量2个近似波形差异的误差矢量幅度(Error Vector Magnitude,EVM)参数来评估时域补偿算法的性能。具体由式(11)计算信号e(n)的EVM,即: (11) 式中:求和范围5 000~9 999是信号e(n)的后段,以确保式(11)中的滤波器输出平稳。 表2 DPD中采用搜索方法对信号时延补偿后的EVMTab.2 EVM of signal after time delay compensation by LUT method in DPD 表3 DPD中采用本文2.2节所述算法对信号时延补偿后的EVMTab.3 EVM of signal after time delay compensation by algorithm described in section 2.2 对比表2和表3可以发现,在DPD系统中若采用本文所述的信号时延补偿算法可以获得不大于搜索法可实现的EVM。 采用文中所述的信号补偿算法可以实现DPD两激励信号的时域补偿。由于本文中信号时延估计算法无需对信号进行高倍内插运算与抽取运算,同时,信号时域对齐处理所用“插值”滤波器的系数无需额外查找表或复杂的迭代运算,因此其运算量低,可极大地简化DPD系统的实现电路,从而确保了超宽带信号数字预失真对运算时效性的要求。文中所述算法有待进一步提升性能之处:① 取自图1所示的PA输出信号必然存在一定的外界干扰,当电路适配时,这一外界干扰对文中所述时延估计算法的鲁棒性有待进一步研究;② 不同的窗函数类型与滤波器的长度对补偿后的DPD信号的波形影响有待进一步分析。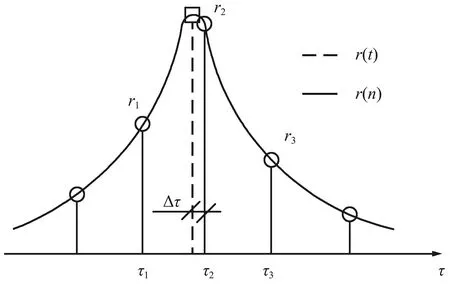
1.2 信号时域对齐
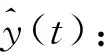
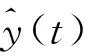
2 算法及其实现
2.1 信号时延估计
2.2 信号时域补偿
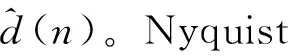
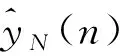
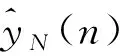
3 算法数值分析
3.1 信号分数时延数值分析
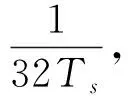

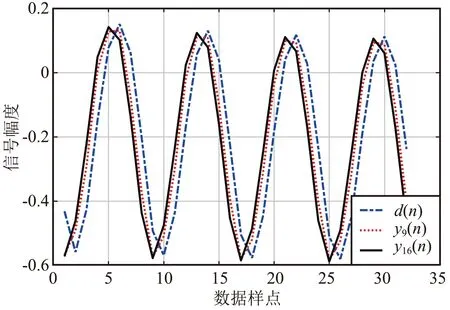
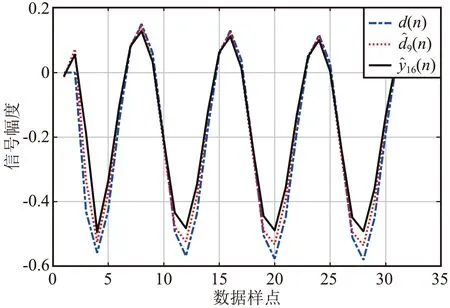
3.2 信号时域补偿数值分析
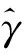
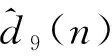
3.3 时域补偿算法对DPD性能数值分析
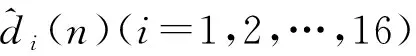

4 结束语
