基于GJO-MLP的露天矿边坡变形预测模型

刘光伟， 郭直清， 刘威

（1. 辽宁工程技术大学 矿业学院，辽宁 阜新 123000；2. 辽宁工程技术大学 理学院，辽宁 阜新 123000）

0 引言

露天矿开采一般采用从上至下、分台阶方式对矿物进行挖掘，由于其开采方式简单且相对于地下开采方式具有更强的安全性，故已成为当前我国矿山中最常见的开采方法之一[1]。然而在实际露天开采过程中，随着生产规模的不断扩大和开采深度的不断增加，矿坑四周逐渐形成了大量高陡边坡，导致边坡变形灾害发生的概率增大[2-3]。有研究表明，边坡变形已成为当前露天矿生产建设过程中的主要灾害之一[4]。因此，为保障露天矿的安全生产，预防边坡垮塌事故的发生，实现矿山滑坡的早期预测预警，对露天矿边坡变形进行科学有效的监测并做出及时准确预测具有十分重要的工程意义[5]。

矿山边坡变形是指在露天矿开采过程中，伴随开采计划不断进行，受人为因素、地质条件及生产状态等多种环境因素影响，边坡出现高维非线性、复杂动态性形变的过程[6-10]。为更好地分析边坡变形过程，许多专家学者提出了一系列有意义的预测方法，其一般以传统预测方法为主[11-14]，但由于边坡变形的高维非线性和复杂动态性等特点，导致传统以经典数学为基础的预测方法在实际生产中难以起到预期效果[15]。近年来随着计算机硬件技术和测绘技术的不断发展，实时监测边坡位移量已成为现实，故基于实时边坡位移监测数据建立基于智能优化算法的人工智能预测方法，对提高边坡位移预测精度、实现矿山灾害预防和安全管理至关重要。

因此，基于智能优化算法的人工智能边坡位移预测方法也被提出并得到了成功应用。陈兰兰等[16]将遗传算法和BP神经网络相结合，有效提高了露天矿边坡变形监测点的预测精度。杨勇等[4]提出改进粒子群优化极限学习机模型，实现了对露天矿边坡监测数据的有效预测。张研等[17]提出了基于粒子群优化相关向量机的矿山边坡变形预测模型，实验结果表明了该方法具有较高的准确性。此外，基于麻雀搜索算法优化支持向量机的边坡失稳智能预测模型[18]、基于改进灰狼算法优化支持向量机的露天矿边坡变形预测模型[19]、融合多层感知机和优化支持向量回归的滑坡位移预测模型[20]、基于改进粒子群算法优化的小波核函数支持向量机边坡变形预测模型[21]等以智能优化算法与人工智能算法相结合的边坡变形预测模型均得到了广泛应用并取得了有意义的结果。

上述研究各有所长，都在不同时期对边坡变形预测做出了有意义的研究成果。但根据无免费午餐定理[22]可知，没有任何一种算法可以解决所有的问题。因此，本文基于N. Chopra等[23]在2022年受金豺协作狩猎行为启发提出的金豺优化（Golden Jackal Optimization，GJO）多层感知机（Multilayer Perceptron，MLP），提出了基于GJO-MLP的边坡变形预测模型，并将其应用于实际的露天矿边坡位移监测中，以验证其可行性。在6个数据集上的仿真实验结果表明：无论是在分类任务还是在预测任务上，GJO-MLP都具有更好的寻优性和更高的收敛性能。将其应用到2个边坡变形预测实例中，结果表明：相较于对比算法，GJO-MLP具有更小的绝对误差和更高的预测精度，充分表明了基于GJO-MLP的边坡变形预测模型的有效性和可行性。

1 相关基础理论

1.1 GJO算法

GJO算法寻优过程主要包括以下3个阶段：初始化种群阶段、搜索猎物阶段、包围并攻击猎物阶段。

1.1.1 初始化种群阶段

GJO算法作为一种群智能优化算法，算法初始解均匀分布在搜索空间上，定义为

式中：Y0为初始金豺种群的位置；Ymax和Ymin分别为金豺种群中的最大位置和最小位置；r为[0，1]上的均匀随机数。

在GJO算法中，猎物初始位置矩阵定义为

式中Yi,j为第i（i=1，2，···，n，n为猎物数量）个猎物对应求解问题的第j（j=1，2，···，d，d为所求解问题的变量数量）个变量的位置。

在算法迭代优化过程中，采用适应度函数来估计每个猎物的适应度值，所有猎物的适应度值矩阵为

式中f（·）为适应度函数，适应度最优的被称为公豺，次优的被称为母豺。

1.1.2 搜索猎物阶段

金豺的天性让其能够在自然界中感知并追踪猎物，但猎物不会被轻易捕获。因此，金豺就会等待和寻找其他的猎物。金豺的狩猎行为是由雄性领导、雌性跟随的，该行为定义为

式中：Y1(t)和Y2(t)分别为第t次迭代时与猎物对应的雄性和雌性金豺的更新位置；YM(t)和YFM(t)分别为第t次迭代时雄性金豺和雌性金豺位置；E为猎物躲避金豺的能量；rl为一个基于莱维分布的随机数；P(t)为第t次迭代时的猎物位置。

式中：E1为猎物的下降能量；E0为猎物的初始能量；c1为常数，取值为1.5；T为最大迭代次数。

综上，金豺的位置更新公式为

式中Y(t+1)为第t次迭代后的金豺位置。

1.1.3 包围并攻击猎物阶段

当猎物受到金豺的骚扰时，其逃逸能量降低，然后豺对（雄、雌金豺）包围并逼近猎物，该过程表述为

综上可知，GJO算法的具体实现流程如图1所示。

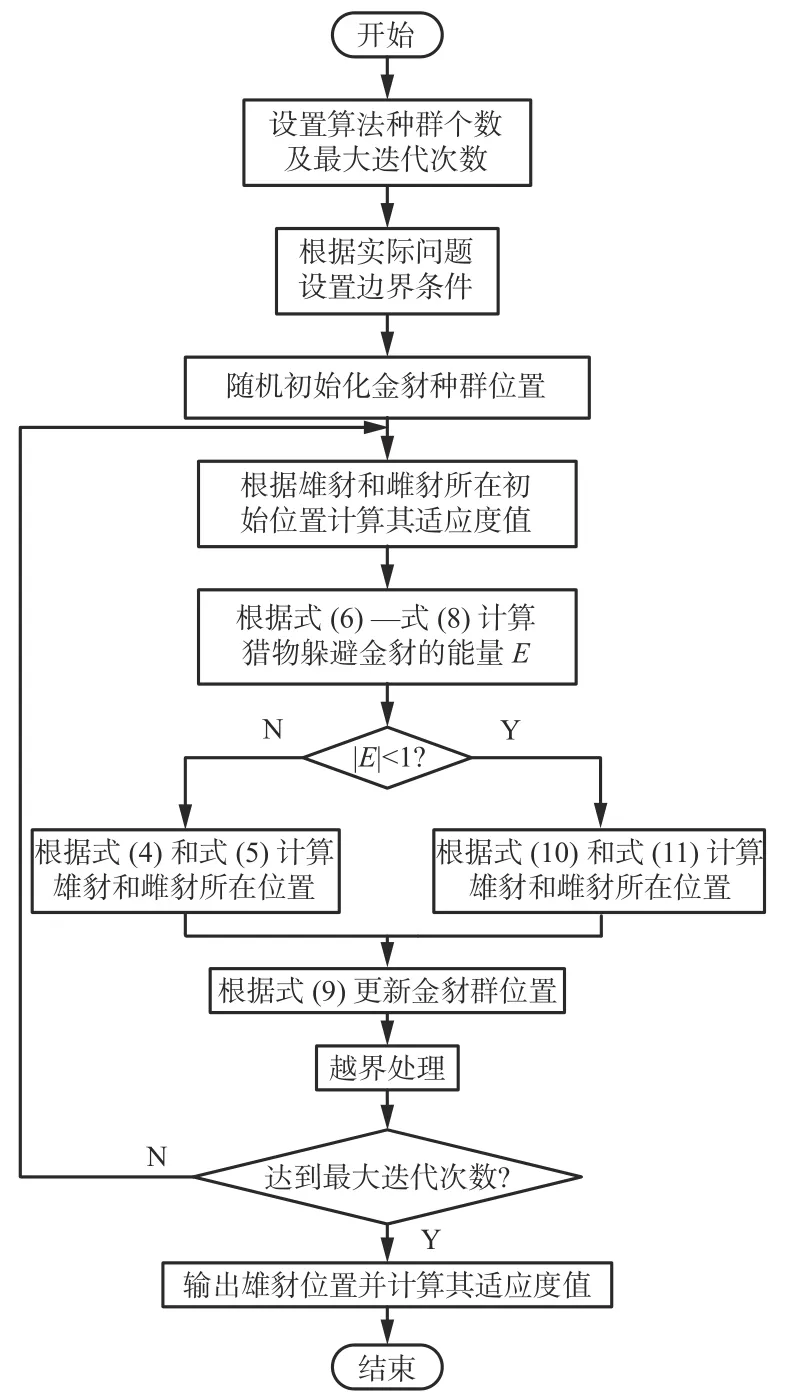
图1 GJO算法流程Fig. 1 Flow of GJO

1.2 MLP

MLP是一种模拟生物神经元结构而提出的数学计算模型，通常被称为前馈神经网络或人工神经网络（Artificial Neural Network, ANN）。由于其结构简单、可解释性强且能对线性和非线性变化数据进行有效分类和预测，常被用于数据工程和机器学习。MLP结构一般包含输入层、隐层和输出层3个部分，输入层到隐层、隐层到输出层之间使用全连接方式进行连接。同时在MLP模型中，输入层到隐层、隐层到输出层的激活函数均为sigmoid函数。其中含1个隐层的MLP模型结构如图2所示。

图2 MLP模型结构Fig. 2 Topology of MLP

针对1组滑坡检测数据集，将其作为MLP模型的输入向量，则MLP模型从输入层到隐层计算过程为

式中：Sb为隐层第b（b=1，2，···，h，h为隐层节点数）个节点输出值；Wab为输入层第a（a=1，2，···，u，u为输入层节点数）个节点到隐层第b个节点的权重；Xa为第a个输入节点，即滑坡位移量；θb为隐层第b个节点的偏置。

隐层到输出层的计算过程为

式中：Ok为输出层第k（k=1，2，···，m，m为输出层节点数）个节点输出值，即边坡变形的预测结果；Wbk为隐层第b个节点到输出层第k个节点的权重；为输出层第k个节点的偏置。

1.3 算法融合可行性分析

在不考虑其他条件的影响下，本节主要探索将GJO算法与MLP融合的可行性，以及将融合后模型用于露天矿边坡监测数据分析预测的可行性。

GJO算法只能求解有明确数学模型的工程问题，对于只含有数据而无具体数学模型的问题无法有效解决。当MLP模型遇见超高维和大规模等复杂性强的数据集时，MLP模型中的隐层数、权值和偏置参数难以确定，且模型易出现梯度爆炸，从而致使模型失效。因此，将GJO算法搜索能力强的特点与MLP模型泛化性强的特点相结合，对求解实际复杂问题具有重要意义。

对于露天矿边坡变形预测，由于露天矿边坡变形受多种因素影响，如地质结构、水文地质条件、采矿活动等，使得预测模型复杂，难以准确捕捉所有影响因素。随着计算机科学技术的迅速发展，越来越多监测设备被部署在露天矿边坡周围，用于实时记录露天矿边坡位移数据。这些数据往往都具有高维度、时序关联性及非线性等特性，如果在其他条件未知而只有数据的情况下，使用传统的边坡稳定性分析方法无法有效进行边坡变形预测。因此，在其他外部条件未知的情况下，采用仅基于数据的模型对露天矿边坡位移数据进行预测对边坡稳定性的事前分析也显得十分必要。鉴此，本文将GJO算法和MLP模型相结合，用于露天矿边坡位移数据预测中。

2 基于GJO-MLP的边坡变形预测模型

2.1 模型原理

若固定MLP模型隐层数，则GJO-MLP预测模型关键在于利用GJO算法寻找MLP模型的最优权值和最优偏置，然后再根据最优权值和最优偏置确定最佳MLP模型，最后再将最佳MLP模型用于边坡变形数据预测。

由于GJO算法以向量形式接收变量并对变量进行迭代寻优，所以利用GJO算法训练最优MLP模型实质上是对由MLP模型权值和偏置构成的参数向量进行寻优，该参数向量定义为

为评价训练得到的MLP模型预测结果，通常使用均方误差（Mean Squared Error，MSE）计算公式进行判别，即

式中：S为MSE；为第a个输入节点在使用第q（q=1，2，···，Q，Q为样本总数）个样本时的期望输出，即第q个样本的预测结果；为第a个输入节点对应的第q个边坡变形的真实数据。

显然，为保证MLP模型整体预测结果的有效性，需要使用所有样本的平均MSE对MLP模型进行评估，即

因此，使用GJO算法训练MLP模型的问题可转换为对MLP模型权值和偏置构成的参数向量迭代寻优的过程，即对最小平均MSE的求解过程。

利用GJO算法训练MLP模型的过程如图3所示。

图3 GJO算法训练MLP模型过程Fig. 3 GJO training MLP model process

由图3可知，根据GJO算法的雄豺引导雌豺的迭代寻优方式，在GJO对最佳MLP模型进行迭代训练过程中，首先根据雄性金豺狩猎方式对初始MLP模型进行权值和偏置的更新，并引领雌性金豺同步对初始MLP模型进行权值和偏置更新，接着采用式（9）融合雄性和雌性金豺对MLP模型的权值和偏置更新特点得到可行MLP模型，最终经可行MLP模型更新得到最优MLP模型。

2.2 模型实现过程

基于GJO-MLP的边坡变形预测模型的基本实现步骤如下。

步骤1：数据预处理。

步骤2：划分数据集并确定训练集和测试集大小。按照20%为测试集和80%为训练集对预处理后的边坡数据集进行划分。

步骤3：构建初始MLP模型。

步骤4：根据式（15）和式（16）计算MSE。

步骤5：判断当前MSE与上一次MSE是否无明显差异（是否为最小MSE）。若无明显差异，则执行步骤8；否则执行步骤6。

步骤6：根据图1执行GJO训练过程。

步骤7：判断经GJO训练出的权值和偏置是否为最优权值和偏置。若为最优权值和偏置，则执行步骤8，否则执行步骤7。

步骤8：根据训练得出的最优权值和偏置构建最优MLP模型，即得到基于GJO-MLP的边坡变形预测模型。

步骤9：利用基于GJO-MLP的边坡变形预测模型对测试集进行预测，得出最后的边坡变形预测值。

2.3 数值仿真实验

为检验GJO-MLP的可行性和有效性，在保证各算法基本参数一致的条件下，将GJO-MLP分别与基于蚁群算法优化的MLP（ACO-MLP）[24]、基于引力搜索算法优化的MLP（GSA-MLP）[25]及基于差分进化算法优化的MLP（DE-MLP）[26]进行对比分析，主要选取了6个数据集进行仿真实验。

2.3.1 实验环境与数据集

操作系统为64位Windows 11，CPU为12th Gen Intel（R） Core（TM） i5-12500H 2.50 GHz；内存为8 GB。

本文选取的6个数据集详细信息见表1。

表1 数据集详细信息Table 1 Datasets details

2.3.2 基本参数设置

为客观有效地保证GJO-MLP与ACO-MLP、GSA-MLP及DE-MLP在进行仿真实验时的公平性，对各算法的基本初始参数进行限制，设置各算法的基本参数，见表2。

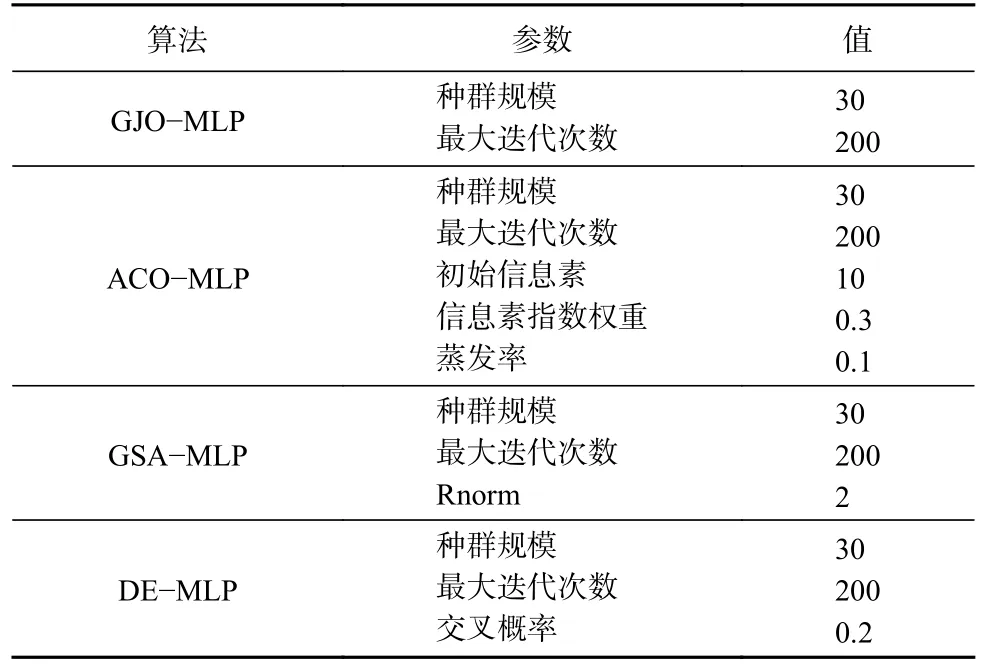
表2 算法参数设置Table 2 Algorithm parameter settings

同时，针对各数据集属性的不同，为保证各实验对比的有效性和客观性，对MLP初始模型结构进行了限定，MLP初始模型结构详细信息见表3。

表3 MLP初始模型结构Table 3 MLP initial model structure

2.3.3 实验结果与分析

为验证本文提出的GJO-MLP具有更好的优越性能，选取6个数据集并将其分别与ACOMLP、GSA-MLP以及DE-MLP进行10次独立重复实验，得到不同算法在10次独立实验下的统计结果，见表4。其中AVE，STD分别代表算法在10次实验中取得的MSE均值和标准差值。由表4可得如下结果。

表4 数据集实验结果Table 4 Classification datasets experimental results

1） 针对Ballon，Iris，Breast cancer，Heart 4个数据集，首先从分类精度上来看，GJO-MLP除在Balloon数据集上的分类精度低于ACO-MLP外，在其余3个数据集上的分类精度均高于其余算法，特别在Breast cancer数据集上，本文提出的GJO-MLP取得了98%的分类精度，远远高于其余3种算法；其次从评价指标MSE上来看，GJO-MLP在4个数据集上的平均MSE指标均为最佳，但其MSE的标准差在4个数据集上均劣于ACO-MLP（但优于其余2个对比算法），这是由于ACO-MLP在迭代寻优过程中陷入了局部最优，导致每次独立重复实验时得到的最优解都几乎一致，故导致了ACO-MLP的标准差最小。

2） 针对Cosine，Sine 2个数据集，首先从算法测试误差上来看，GJO-MLP在2个数据集上的测试误差均最小，表明其具有更好的预测结果；其次从MSE指标上来看，GJO-MLP除在Sine数据集上略微低于DE-MLP外，在其余对比算法和Cosine数据集上都表现出了最优性能，同时MSE的标准差也仅次于ACO-MLP。

为更清晰地观测出各算法在数据集上的迭代寻优性能，本文绘制出各算法在6个数据集上的迭代收敛曲线，如图4所示。由图4可知，本文提出的GJO-MLP除在Sine数据集上的收敛速度略微慢于DE-MLP外，在其余数据集上的收敛速度均快于其他对比算法，再次表明了GJO-MLP具有更佳的收敛性能和寻优性能。

图4 各算法在不同数据集上的迭代收敛曲线Fig. 4 Iterative convergence curve of each algorithm under different datasets

综上所述，在同一约束条件下，本文提出的GJO-MLP不仅有更优的指标值（MSE指标、分类精度与测试误差值），而且在函数的迭代寻优上具有更快的收敛速度。

3 工程实例分析

为将GJO-MLP更好地应用于露天矿的边坡变形预测中，本文选取国能宝日希勒露天矿采东1线东帮685边坡观测数据及文献[27]中的花坪子边坡数据进行预测分析。同时为更进一步验证GJOMLP具有更好的收敛性能和寻优性能，将GJO-MLP与ACO-MLP、GSA-MLP及DE-MLP进行对比分析，最后通过分析边坡变形的实际数据与预测数据的绝对误差来评价算法性能。

3.1 宝日希勒露天矿边坡变形预测

宝日希勒露天矿区位于内蒙古呼伦贝尔市陈旗煤田东部，南北宽5.86 km，东西长10.98 km，共划分为5个采区。该露天矿边坡主要由粉砂岩、砂质黏土、腐殖土、砾石砂岩等组成，属于典型的软岩边坡；同时，受地下水及地层特性等诸多因素的共同影响，其边坡稳定性较差。

本文采集宝日希勒露天矿采东1线东帮685监测点从2022年10月1日到2022年10月26日的3 655条基础数据（2次边坡数据间间隔10 min）进行算法预测分析。对宝日希勒露天矿采东1线东帮685监测点的边坡变形预测的步骤如下。

步骤1：数据预处理。由于原始边坡数据的间隔较短，导致边坡的变形情况未发生较大改变，为更好地分析该地的边坡变形情况，本文按照班次对边坡变形数据进行预处理，即每隔8 h采集1次边坡变形数据，最终得到处理后的数据集，见表5。

表5 东帮685观测点变形监测数据Table 5 Deformation monitoring data of Dongbang 685 mm

步骤2：划分数据集。按照3∶1比例对预处理后数据集进行划分，其中80%为训练集，20%为测试集。

步骤3：算法预测。按照2.2节中的基于GJOMLP的边坡变形预测模型实验步骤对宝日希勒露天矿采东1线东帮685监测点进行预测（MLP模型结构为1-15-1）。

步骤4：算法对比与结果分析。分别利用ACOMLP、GSA-MLP和DE-MLP算法对宝日希勒露天矿采东1线东帮685监测点进行预测，并将其预测结果与GJO-MLP预测结果进行对比分析，同时与实际的边坡变形监测数据进行对比，以验证本文提出的GJO-MLP的有效性。

由表5可知，采集到的数据为边坡在空间坐标系下的3个位移分量，而在实际工程中判断边坡是否发生滑坡的关键参数是水平位移，因此，本文只考虑其水平位移量的绝对值。4种算法对宝日希勒露天矿采东1线东帮685观测点变形监测数据的预测结果及各算法预测值与实际监测值之间的绝对误差见表6，绝对误差越小，说明算法性能越好。表6中粗体代表绝对误差最小，即预测结果与实际监测结果越接近。4种算法对宝日希勒天矿采东1线东帮685观测点变形监测数据的预测误差如图5所示，预测误差越靠近横坐标，代表算法性能越好。

表6 4种算法对东帮685观测点变形监测数据的预测结果Table 6 Prediction results of deformation monitoring data of 685 observation points in Dongbang by four algorithms mm

图5 4种算法对东帮685观测点变形监测预测误差Fig. 5 Prediction error of deformation monitoring of 685 observation points in Dongbang by four algorithms

结合表6和图5可知，在相同实验条件下，GJO-MLP对宝日希勒露天矿采东1线东帮685监测点的边坡预测结果相对于ACO-MLP、GSA-MLP和DE-MLP在整体上具有更小的绝对误差，表明GJO-MLP的预测性能优于对比算法，同时也显示出GJO-MLP预测结果更接近实际边坡位移监测值，验证了GJO-MLP在边坡变形预测中的可行性。

综上可知，GJO-MLP在对边坡变形进行预测时，不仅具有较强的预测优化性能，而且具有较好的可行性。

3.2 花坪子边坡变形预测

为进一步验证本文提出的GJO-MLP的有效性并提升实验结果的可靠性，采用文献[27]中的花坪子边坡底部观测点TP02-HPZ在垂直方向上的累计位移作为实验变形数据再次进行仿真模拟实验。其中数据观测时间为2018年1月1日到2018年4月30日，累计120期数据。在本实验中，以前110期数据作为训练样本，后10期数据作为测试样本；实验对比算法及相应参数除MLP结构外均与3.1节一致（MLP模型结构为1-10-1）。

4种算法对花坪子边坡底部观测点TP02-HPZ变形监测数据的预测结果及各算法预测值与实际监测值之间的绝对误差见表7。4种算法预测结果与实际监测值如图6所示。4种算法对观测点TP02-HPZ的预测绝对误差和如图7所示。

表7 4种算法对花坪子边坡TP02-HPZ的预测结果Table 7 Prediction results of TP02-HPZ of Huapingzi slope by four algorithms mm

图6 4种算法对花坪子边坡观测点TP02-HPZ的预测结果Fig. 6 Prediction results of TP02-HPZ of Huapingzi slope observation point by four algorithms

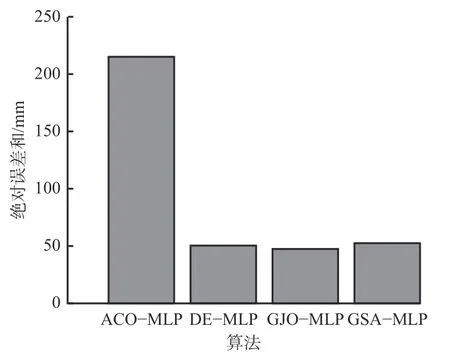
图7 4种算法对观测点TP02-HPZ的预测绝对误差和Fig. 7 The sum of the forecast absolute errors of the four algorithms for the observation point TP02-HPZ

由图6可知，利用4种算法对花坪子边坡底部观测点TP02-HPZ的最后10期数据进行预测时，从折线图的整体趋势来看，DE-MLP的预测结果更接近实际监测值，而GJO-MLP预测效果略逊于DE-MLP，但2种算法都表现出较好的预测能力，而ACO-MLP和GSA-MLP的预测结果则相对较差。虽然GJOMLP预测性能在直观上劣于DE-MLP，但结合表7可知，GJO-MLP的绝对误差均小于0.1 mm，优于其余3种对比算法，同时结合图7可知，GJO-MLP的绝对误差和最小。故从整体上来看，使用GJO-MLP对花坪子边坡底部观测点TP02-HPZ的最后10期数据进行预测时不仅能够获得更好的预测值，而且具有更强的鲁棒性。

4 结论

1） 建立了GJO-MLP算法，并在6个数据集上进行了仿真实验。实验结果表明：在相同实验条件下，相较于其他3种算法，GJO-MLP表现出更好的寻优性能。

2） 建立了基于GJO-MLP的边坡变形预测模型并将其应用于宝日希勒露天矿边坡变形预测和花坪子边坡变形预测。结果表明：在相同条件下，相较于对比算法，基于GJO-MLP的边坡变形预测模型在对边坡变形数据进行预测时不仅表现出更好的预测求解性能，而且还具有更好的可行性和鲁棒性。

3） 基于GJO-MLP的边坡变形预测模型虽然在2个边坡预测问题中都表现出良好的性能，但其得到的结果不能作为最终的边坡失稳判定条件。该模型只适用于在未知其他外部环境下（只有边坡变形监测数据）时的简易边坡变形预测方法，得到的结果只能作为露天矿边坡稳定性分析中的一部分，而不能作为最终的边坡稳定性判别结果。更合理的边坡变形预测模型应该是在力学、地质学、管理学和数学等多学科交融下建立的模型，然后再根据模型预测结果做出最终的综合决策，而不仅仅是基于某些单一因素或监测数据就可得出结论。

4） GJO-MLP算法时间复杂度过高，不能进行实时预测预警，只适用于阶段预测问题（如月度指标预测、季度指标预测和年度指标预测等）。因此，后续研究将从改进GJO算法以提高其收敛速度的角度出发，同时会搭建相应的基于人工智能算法的边坡变形预测预警框架并将其嵌入到现有的边坡位移监测软件当中，真正实现对露天矿边坡的实时预控。