单滚柱包络端面蜗杆传动效率建模及分析
2023-10-12吴洪东
吴洪东
(广州市机电技师学院,广东广州 510430)
0 前言
蜗杆传动是在空间交错的两轴间传递运动和动力的一种传动机构,具有传动比大、结构紧凑、传动平稳等特点,广泛应用于机床、仪器、起重运输机及建筑机械中。然而与齿轮传动等方式相比,蜗杆传动存在传动效率低的缺点。对此,诸多学者针对如何提高蜗杆传动效率展开了研究,提出了一系列具有活动齿包络蜗杆传动形式[1-5]。这种传动方式主要通过蜗轮活动齿的自身旋转,将常规蜗杆传动的滑动摩擦转变为滚动摩擦,以减少滑动摩擦损失,提高传动效率。单滚柱包络端面蜗杆传动就是一种活动齿包络蜗杆传动方式[6],端面啮合蜗杆齿面是由以滚子齿面为母面包络展成。许多学者对单滚柱包络端面蜗杆传动的啮合理论、模型创建、自转特性、瞬态动力、弹流润滑、闪温特性、设计加工等进行了大量研究[7-11]。本文作者在啮合理论基础上,以传动效率为研究对象,建立单滚柱包络端面蜗杆数学模型,分析影响传动效率的主要因素,通过仿真进行优化计算。
1 单滚柱包络端面蜗杆传动建模
单滚柱包络端面蜗杆传动三维模型如图1所示,包括端面蜗杆和滚柱式蜗轮两部分。

图1 单滚柱包络端面蜗杆传动三维模型
蜗轮结构如图2所示,滚柱均匀地分布在蜗轮盘端面上,滚柱可以绕自身中心轴转动。该结构能使蜗轮与蜗杆接触面积增大,接触更加稳定,安装方便且安装精度高。

图2 蜗轮结构示意
1.1 啮合点受力分析
设某一瞬间,在啮合点p处,蜗杆齿面、蜗轮齿面的法向力分别为Fn1、Fn2,切向力分别为Ft1、Ft2,轴向力分别为Fa1、Fa2,如图3所示。
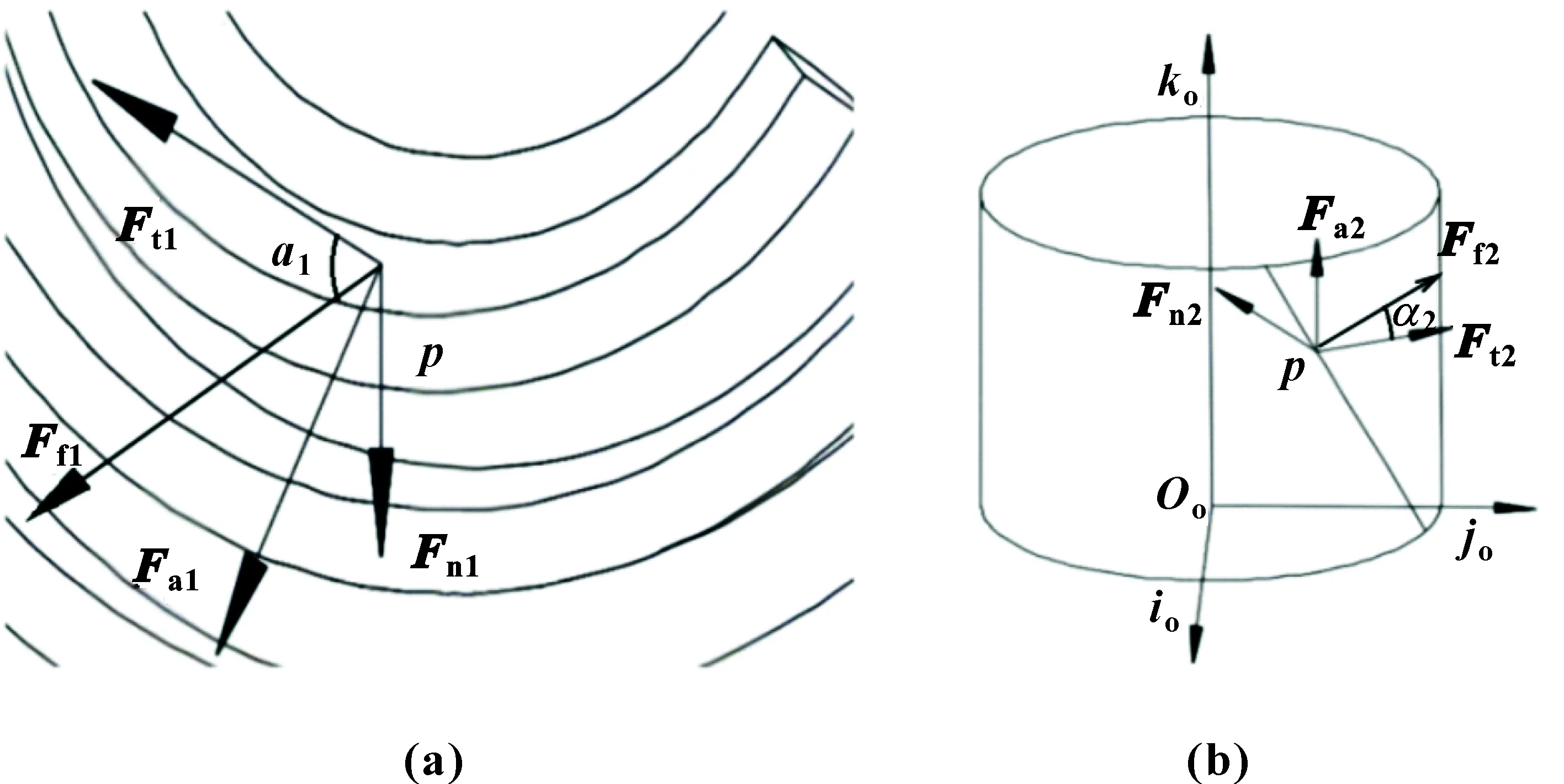
图3 蜗杆(a)、轮齿(b)在啮合点的受力简图
由啮合理论可知,在啮合点p处,蜗杆齿面、蜗轮齿面的相对速度矢量v12的公法向分量为零。由摩擦力的产生原理——源于两接触面或两接触点的相对运动或相对运动趋势推导可知,在啮合点p处,蜗杆齿面、蜗轮齿面的摩擦力公法向分量为零。因此,摩擦力仅存在于两共轭齿面公切面内,即蜗轮、轮齿是在切向力的作用下绕自身轴线转动的。
由以上可知,轮齿在切向力Ft2的作用下绕自身轴线转动,并将此方向的滑动转变为滚动。设滚动摩擦因数与滑动摩擦因数比值为fg,则对轮齿传动效率起影响的作用力为Fn2、Fa2、fgFt2,其合力为
F2=Fn2+Fa2+fgFt2
(1)
由力的平衡条件易知,对蜗杆传动效率起影响的作用力为Fn1、Fa1、fgFt1,其合力为
F1=Fn1+Fa1+fgFt1
(2)
由平衡条件易得:
F2=-F1
(3)
式中:负号仅表示两者方向相反。
设滑动摩擦因数为f,则蜗轮齿面、蜗杆齿面在啮合点p处的摩擦力分别为
Ff1=Fn1f
(4)
Ff2=Fn2f
(5)
其中Ff1、Ff2与啮合点p处的相对速度矢量v12方向分别为相反和相同,则有:
(6)
(7)
式中:α1、α2分别为Ft1与Ff1、Ft2与Ff2的夹角,易知α1=α2。
(8)
式中:A为传动副中心距;R为蜗轮轮齿(滚柱)半径;θ、u为轮齿参数;i21为传动副传动比;φ2为蜗轮转角;k、z2分别为传动副喉颈系数和蜗轮齿数;中间变量a2=A(2-k)(8-5z2)/(10z2)。
由上可知,对蜗轮齿面、蜗杆齿面在啮合点p处的摩擦力产生影响的主要因素有滑动摩擦因数f、喉颈系数k、蜗轮轮齿(滚柱)半径R、蜗轮齿数z2及传动副中心距A等。
1.2 传动效率求解模型
在活动坐标系中,设蜗杆、蜗轮在啮合点p处的速度矢量分别为v1、v2,则蜗杆、蜗轮的功率Pw、Pg分别为
(9)
传动副的瞬时传动效率为
η=Pg/Pw
(10)
单滚柱包络端面蜗杆传动在啮合点p处瞬时传动效率为
(11)
式中:e1、e2、en分别为蜗轮轮齿活动坐标系的基向量。
在啮合点p处,传动副的单齿瞬时传动效率ηu为瞬时传动效率η沿瞬时接触线方向积分后的平均值,即
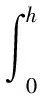
(12)
啮合全齿高h为
(13)
式中:hf、hfc分别为齿根高、齿根高系数,常规情况下两者相等,且一般情况取1或0.8。
单齿平均传动效率ηp为传动副单齿瞬时传动效率ηu沿时间方向或蜗轮转角方向积分后的平均值,即
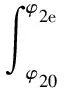
(14)
式中:φ20、φ2e分别为蜗轮转角起始位置、终止位置。
传动副多齿同时啮合,设其同时啮合的齿数为n(n为整数),其瞬时传动效率ηi、平均传动效率ηui分别为
(15)
(16)
式中:φ20i、φ2ei分别为第i齿蜗轮转角起始点与终止点,且有:
(17)
式中:γ为齿距角,其值为360/z2;i值为1,2,3,…,n;φ201=-90-nγ/2。
2 单滚柱包络端面蜗杆传动效率分析
在计算多齿同时啮合传动效率时,将同时啮合的多个蜗轮轮齿视为一个整体,如图4所示。蜗轮结构简图如图5所示。假设同时啮合的蜗轮轮齿数为4,则1—4号位置的蜗轮轮齿为一整体。当1号位的轮齿转动到2号位时,4号位的轮齿同时转动到5位,完成一个啮合周期,即齿距角γ为14.4°,φ2的取值范围为[-118.8°,-104.4°]。运动周期内所计算得到的传动效率即为传动副传动效率。

图4 传动副运动简图
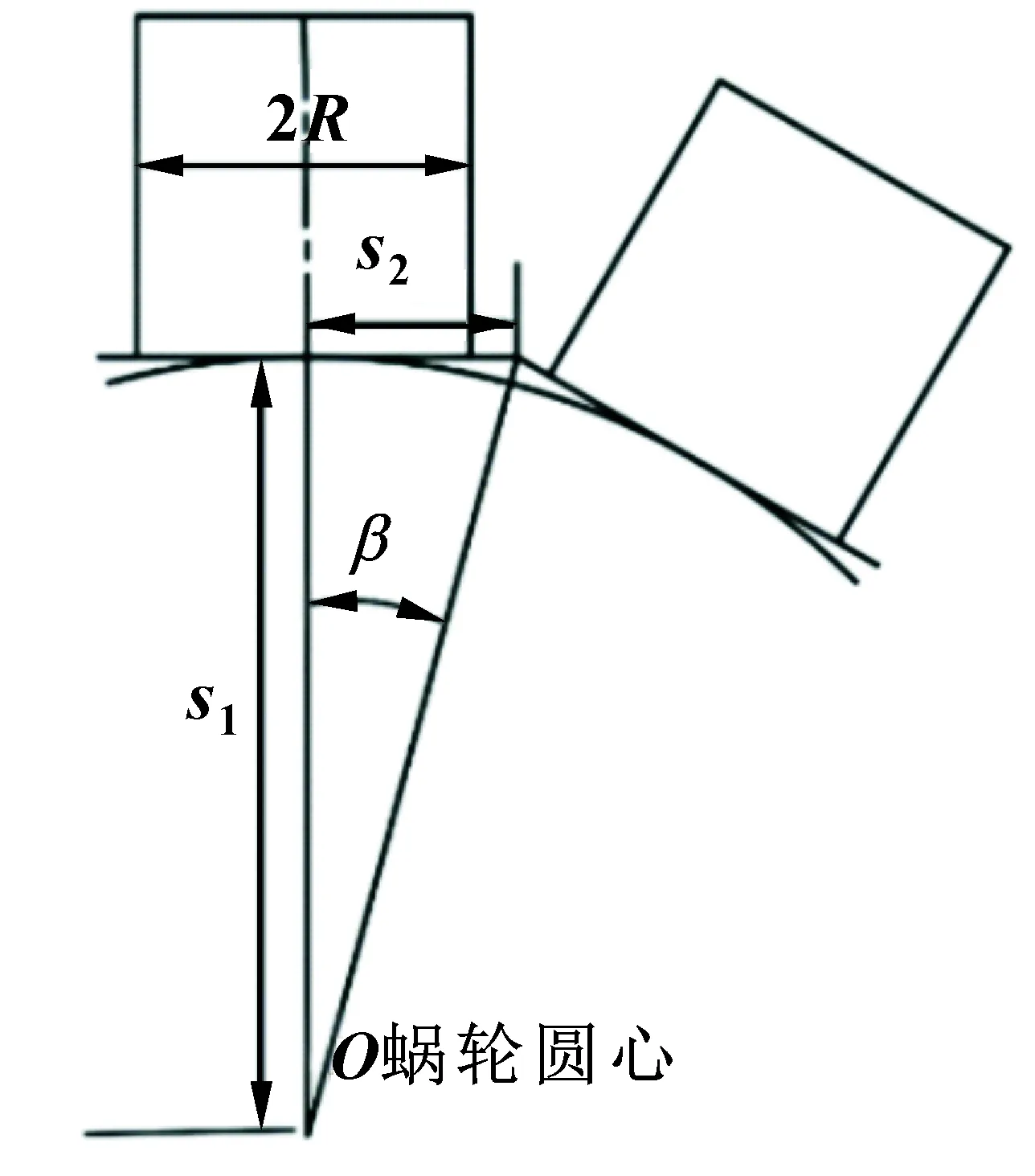
图5 蜗轮结构简图
假设单滚柱包络端面蜗杆传动副由同一种材料加工而成,蜗杆为单头蜗杆,主要参数及参数值如表1所示。采取单一变量法分析某个参数值变动对传动效率影响,其他参数值固定为表1中值。
2.1 蜗轮转角
图6为传动副同时多齿啮合平均传动效率受蜗轮转角φ2的影响曲线。可知:ηun-φ2曲线近乎为直线,传动副瞬时传动效率从啮入至啮出逐渐增大。当滑动摩擦因数f分别取0.05、0.10、0.15、0.2时,啮出时的瞬时传动效率比啮入时分别增大了4.65%、7.63%、9.72%、11.27%。滑动摩擦因数f越大,平均传动效率受蜗轮转角φ2的影响就越大。同时可知,当蜗轮转角为恒定值时,滑动摩擦因数f越大,传动副瞬时传动效率越小。
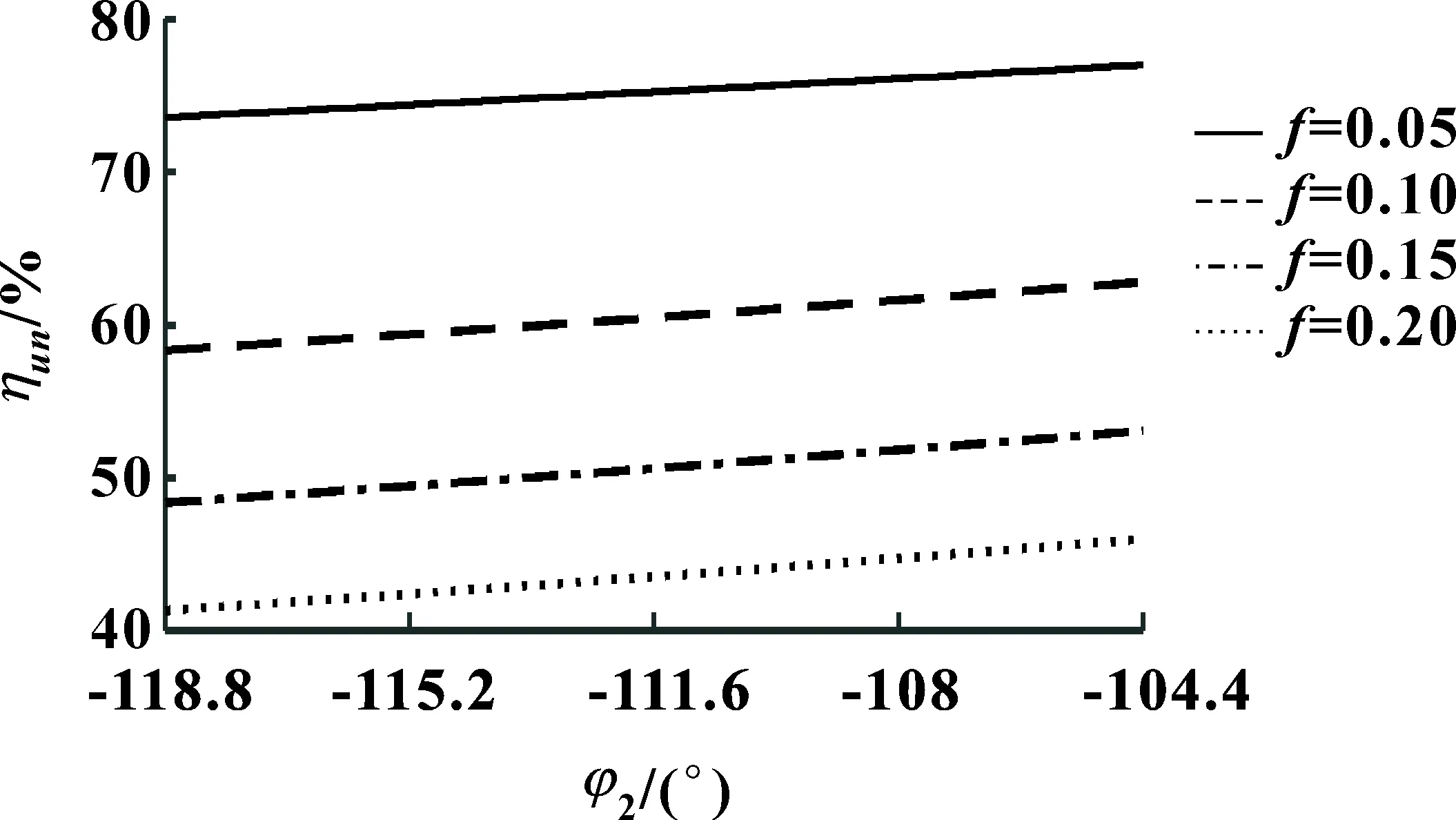
图6 蜗轮转角对瞬时传动效率的影响
2.2 滑动摩擦因数对传动效率的影响
图7为传动副同时多齿啮合平均传动效率受滑动摩擦因数f的影响曲线。可知:在给定参数条件下,传动副的平均传动效率随着滑动摩擦因数f的增大而减小。当滑动摩擦因数f分别为0.05、0.10、0.15、0.2,传动副的平均传动效率分别为75.29%、60.53%、50.67%、43.59%。滑动摩擦因数f从0.05增大到0.2,平均传动效率降低了31.7%。由此可知,单滚柱包络端面蜗杆传动的传动效率受滑动摩擦因数影响较大。
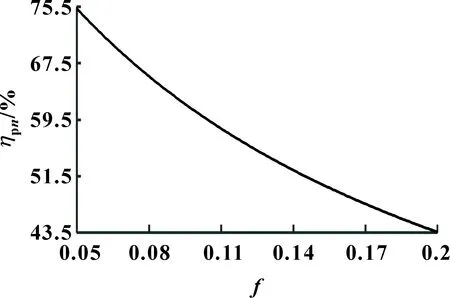
图7 滑动摩擦因数对平均传动效率的影响
2.3 喉颈系数对传动效率的影响
图8为传动副同时多齿啮合平均传动效率受喉颈系数k的影响曲线。可知:在给定参数条件下,传动副的平均传动效率随着喉颈系数k的增大而减小。当滑动摩擦因数f分别取0.05、0.10、0.15、0.2,喉颈系数k从0.30增大到0.50,传动副的平均传动效率分别降低了3.09%、4.93%、6.18%、7.07%。由此可知,滑动摩擦因数f越大,平均传动效率受喉径系数k的影响就越大。
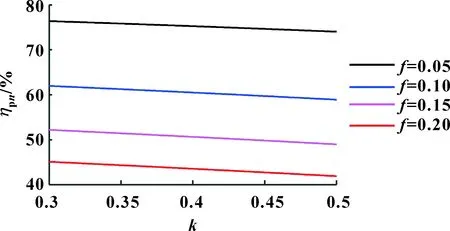
图8 喉颈系数对平均传动效率的影响
2.4 滚柱半径对平均传动效率的影响
图9为传动副同时多齿啮合平均传动效率受滚柱半径R的影响曲线。可知:在给定参数条件下,传动副的平均传动效率随着滚柱半径R增大而略有减小。当滑动摩擦因数分别取0.05、0.10、0.15、0.2,滚柱半径R从5 mm增大到10 mm,传动副平均传动效率分别降低了0.71%、1.14%、1.44%、1.66%。由此可知,滑动摩擦因数f越大,平均传动效率受滚柱半径R的影响就越大。

图9 滚柱半径对平均传动效率的影响
2.5 蜗轮齿数对平均传动效率的影响
图10为传动副同时多齿啮合平均传动效率受蜗轮齿数z2的影响曲线。可知:在给定参数条件下,传动副的平均传动效率随着蜗轮齿数z2的增大而减小。当滑动摩擦因数分别取0.05、0.10、0.15、0.2,蜗轮齿数每增大1,传动副平均传动效率分别降低1.00%、1.61%、2.02%、2.33%。由此可知,滑动摩擦因数f越大,平均传动效率受蜗轮齿数z2的影响就越大。
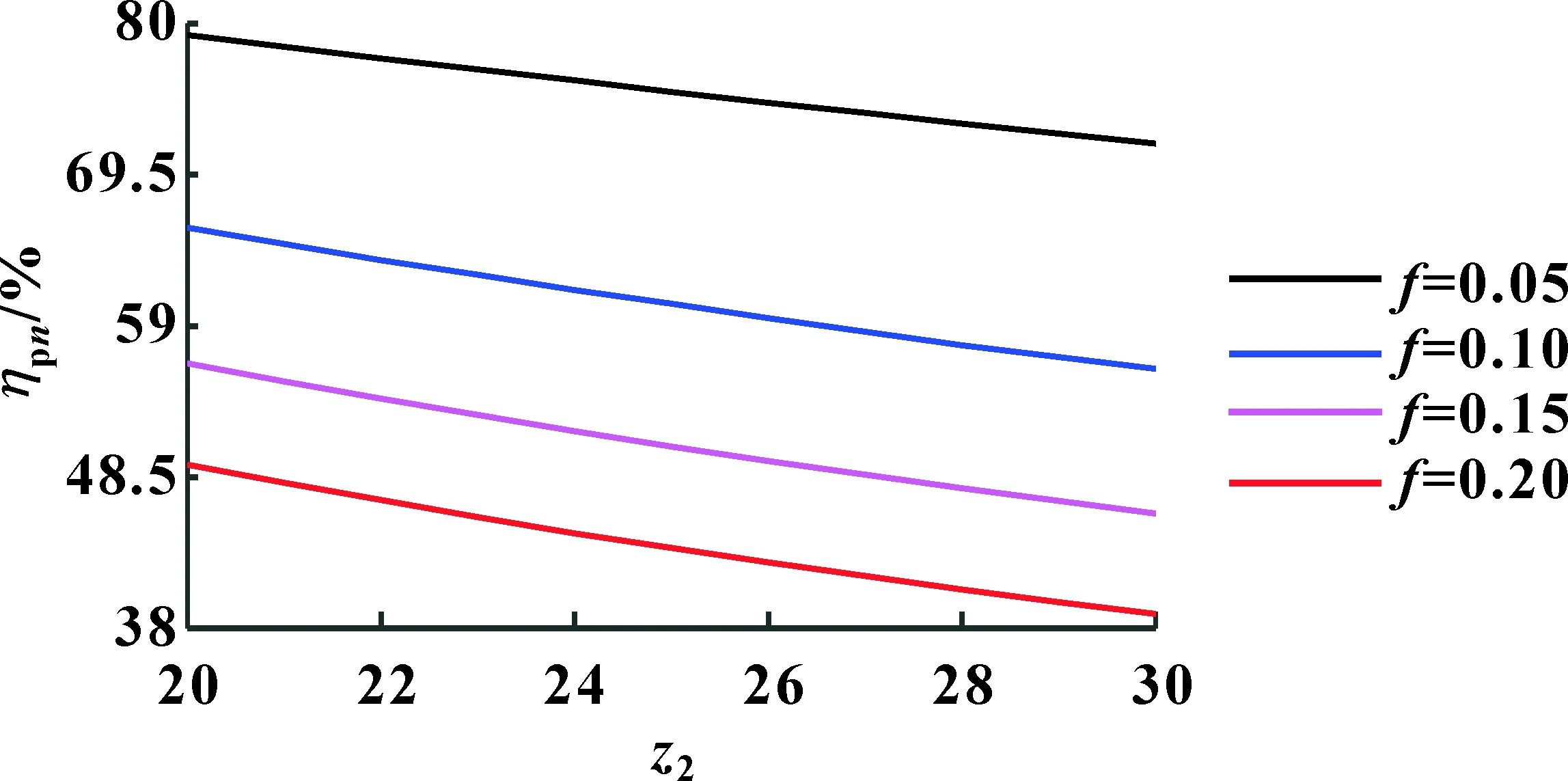
图10 蜗轮齿数对平均传动效率的影响
2.6 中心距对平均传动效率的影响
图11为传动副同时多齿啮合平均传动效率受中心距A的影响曲线。可知:在给定参数条件下,传动副的平均传动效率随着中心距A的增大而略有增大。当摩擦因数分别取0.05、0.10、0.15、0.2,中心距A从160 mm增大到200 mm,传动副平均传动效率分别增大了0.28%、0.46%、0.58%、0.67%。由此可知,滑动摩擦因数f越小,中心距越大,平均传动效率越高。
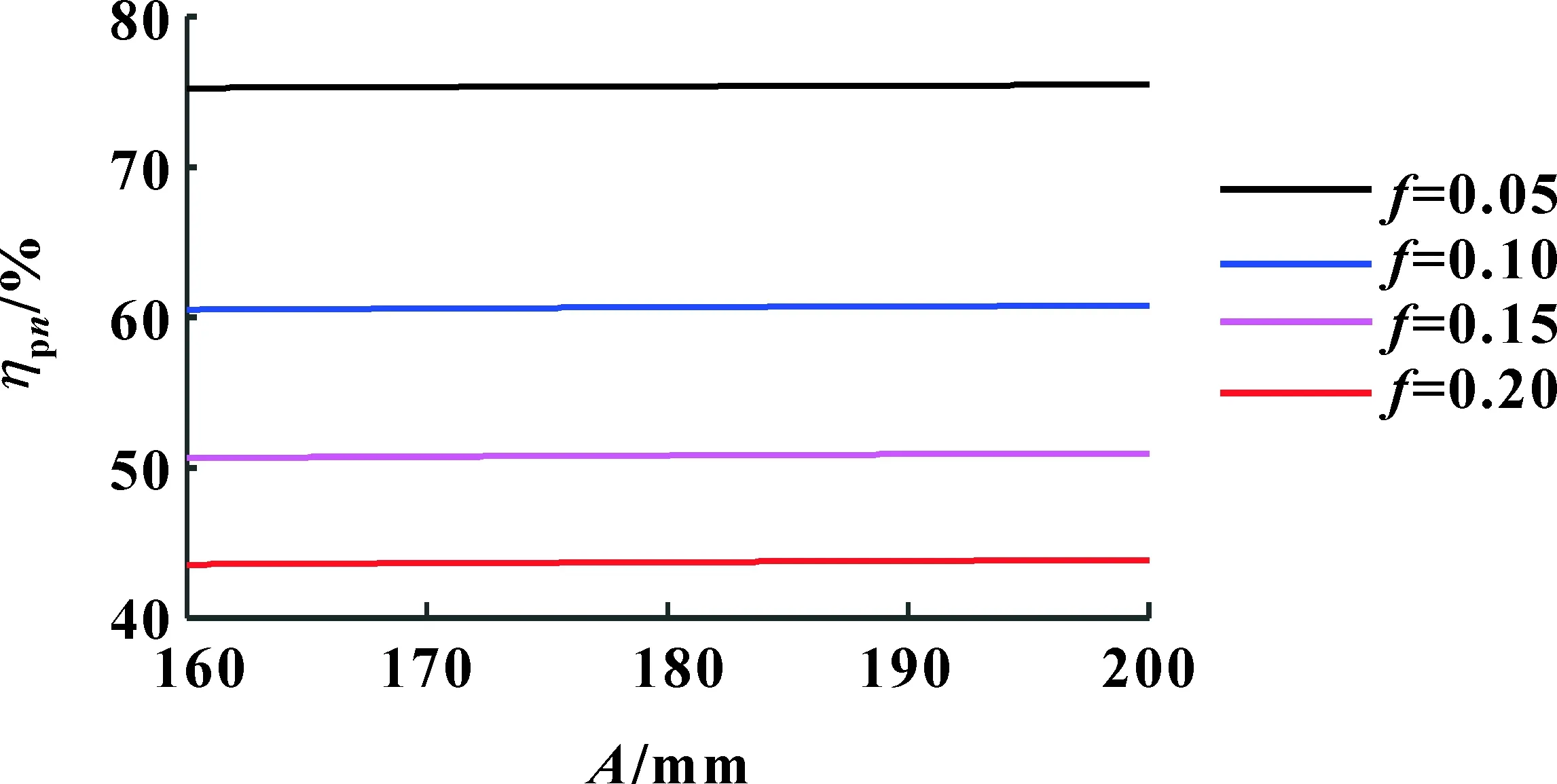
图11 中心距对平均传动效率的影响
综上所述,单滚柱包络端面蜗杆传动效率随着蜗轮转角和中心距的增大而增大,随着滑动摩擦因数、喉颈系数、滚柱半径、蜗轮齿数的增大而减小,即蜗轮转角和中心距越大,滑动摩擦因数、喉颈系数、滚柱半径、蜗轮齿数越小,则传动效率越高。
3 单滚柱包络端面蜗杆传动仿真优化
3.1 建立优化约束函数
建立如下目标变量传动效率ηpn与设计变量喉颈系数k、滚柱半径R、蜗轮齿数z2、中心距A、齿顶高系数hfa、齿根高系数hfc、同时啮合齿数n间的函数关系。
ηpn=g(k,R,z2,A,hfa,hfc,n)
(18)
为避免传动副几何结构出现畸变,如蜗杆齿形变尖,同时满足传动副安装空间尺寸条件及传动平稳性,各个几何参数须满足一定的约束条件。在此各几何参数的约束范围设定为
(19)
(20)
式中:cc为齿顶隙系数,取0.2或0.25,在此取0.2;s1、s2为中间变量。
对滚柱包络端面啮合蜗杆传动而言,其结构优化以传动效率最大化为优化目标。其约束函数为
(21)
3.2 仿真优化计算
基于表1中的几何参数,由式(17)计算得到传动效率值为83.2%,略高于常规蜗杆传动的传动效率。借助MATLAB,以传动效率倒数为优化目标,进行优化计算,其中表2的传动效率分别为采用MATLAB优化工具箱自带的“fmincon”优化指令和遗传优化算法模块优化运行后的结果。
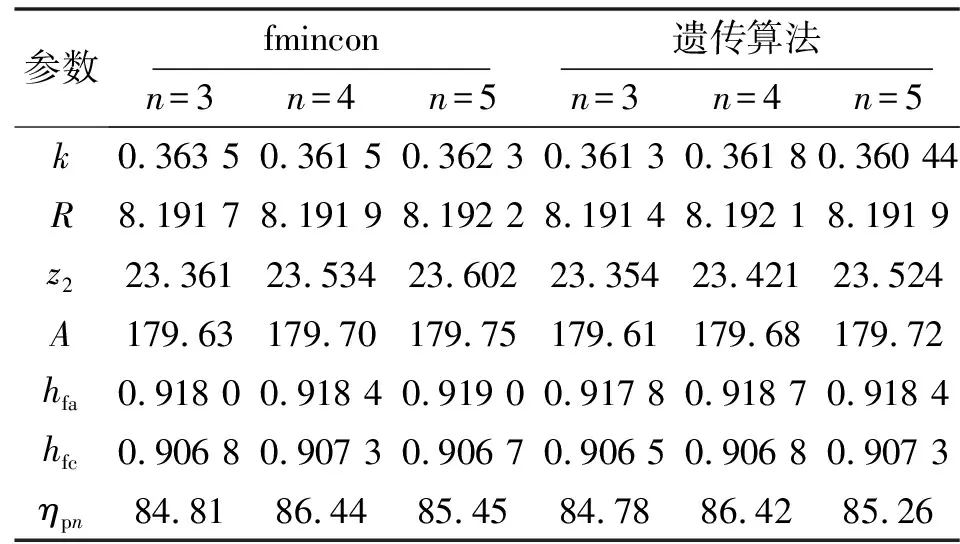
表2 优化后的传动效率
由表2可知,当n为4时,对其他参数值进行适当处理,得到最优解与最优值,分别为k=0.36,R=8.19 mm,A=179.7 mm,hfa=0.92,hfc=0.91,ηpn=86.4%,较采用表1中参数值,传动效率提高了3.2%。
4 结论
基于单滚柱包络端面蜗杆传动理论,建立了传动效率数学计算模型,计算了传动副同时多齿啮合情况下的瞬时传动效率及平均传动效率,分析了摩擦因数、喉颈系数、滚柱半径、蜗轮齿数及中心距等参数对传动副平均传动效率的影响,并以传动效率为优化目标采用MATLAB优化运行计算。研究结果显示:
(1)单滚柱包络端面蜗杆平均传动效率与摩擦因数、喉颈系数、滚柱半径、蜗轮齿数呈负相关,与中心距呈正相关;
(2)摩擦因数对传动副平均传动效率影响最大,传动副主要几何参数中蜗轮齿数对传动副平均传动效率影响最大,中心距对传动副平均动效率影响最小。
(3)遗传算法与指令“fmincon”所代表的算法优化结果相近,且结构优化之后传动效率提升了3.2%。
(4)为了得到单滚柱包络端面蜗杆传动较高的传动效率,除需要精加工外,还应注意在确定中心距的情况下,喉颈系数、滚柱半径、蜗轮齿数不宜过大。
