面向铸件自动化打磨的点云精简方法
2023-10-12朱彬陈新度吴磊刘跃生刁世普
朱彬,陈新度,吴磊,刘跃生,刁世普
(1.广东工业大学机电工程学院,广东广州 510006;2.广东工业大学,省部共建精密电子制造技术与装备国家重点实验室,广东广州 510006)
0 前言
近年来,机器人自动化作业在铸件加工中不断普及[1],打磨作为铸件加工的核心技术之一[2],对其费用、效率、精度影响非常大。因点云不受光照、阴影和纹理等影响的优势,对于感知目标的几何信息具有重要意义[3],可以作为自动打磨加工的数据载体。然而,所得点云受限于硬件设备和扫描环境[4],可能具有较高的冗余度[5]。为了提高处理效率及锐化几何特征,需要对感知的点云进行精简,即删除对曲面几何形状信息贡献较少的冗余点。
但传统曲率点云精简方法存在数据空洞、数据缺失等问题[6]。因此,本文作者提出一种线性耦合曲率精简算法(Simplification of Curvature Linear Coupling Algorithm,SCLCA),在曲率精简的基础上引入曲变[7]参数改善精简效果与抗噪性能;同时在不改变原点云属性的前提下,基于线性耦合曲率参数排序并筛选特征点云,最终完成精简任务。
1 线性耦合曲率特征
点云精简旨在保留原特征同时尽可能剔除冗余数据,如图1所示。如何保留特征信息是点云精简最重要的一环,为了改善传统点云曲率精简的特征锐化性,文中提出了一种线性耦合曲率特征。通过曲率排序改善点云的无序性[8],并引入曲变参数提升特征锐化性。
1.1 特征域提取
点云的无序性使得无法仅从坐标参数判别特征点。因此可将原点云按照一定规律排序,即根据排序提取特征点。其步骤如下:
根据式(1)(2)得到原点云P(图1(b)所示)中各点pi的曲率ρ(pi)后,即可按照式(3)对P排序,得到排序点云Pρ:
(1)
(2)
(3)
即Pρ中各点按照曲率ρ(pi)大小排序。
但由于曲率特征本身具有一定误差[6],因此还需要一种更稳健、精确的排序方法,即线性耦合曲率排序。
1.2 线性耦合曲率排序
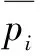
αi=i/N(i=1,…,N)
(4)
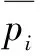
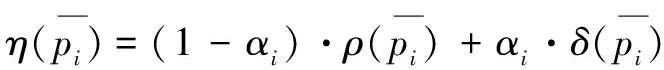
(5)
(6)
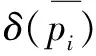
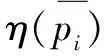
根据式(7)对原点云P第二次排序:
(7)
得到排序点云Pη,再按照序列提取兼具特征锐化性、保形性的特征点云Psig。特征点云提取流程如图2所示。
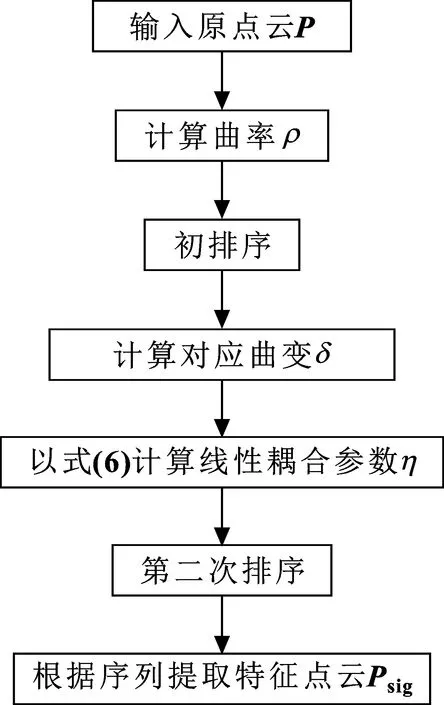
图2 特征点云提取流程
2 精简算法
2.1 非特征域精简
提取特征点云区域Psig后,剩下的非特征区域Punsig仍具有较高冗余度,可按文中提出的改进BSP精简方法继续精简[10]:
首先采用PCA方法构造Punsig的协方差矩阵M(Punsig)并进行奇异值分解:
(8)
2.2 算法流程
通过线性耦合曲率特征得到特征点云P1,以改进BSP方法得到非特征点云域精简结果P2,融合P1、P2即得最终精简结果,流程如图3所示。
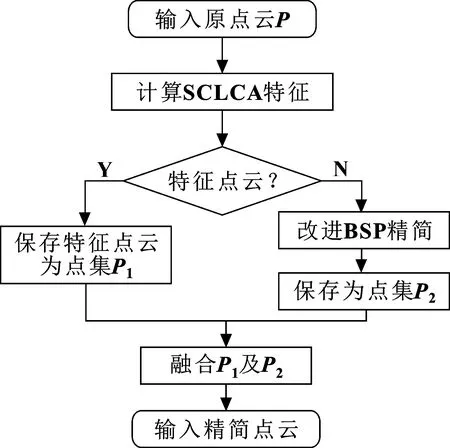
图3 SCLCA算法流程
3 实验与分析
3.1 实验条件
采用图1(b)所示的铸件点云模型、斯坦福Bunny模型为实验对象,研究文中SCLCA算法的精简效果。同时以曲率精简[11]、曲变精简[10]为对比算法,并从精简比、保形性[12]、曲面拟合几个方面进行评价。Bunny模型如图4所示。

图4 Bunny模型
采用保形性误差评判精简效果[11]:
(9)
对于原始点云P中某一点p,pU′为精简点云P′中离p最近的点,n为点p法向量。
保形性误差可评判精简点云与原始点云之间差异程度,保形性误差越小,则精简点云与原始点云间差异越小,精简效果越好。
算法采用C++、PCL点云库编写,Cloud Compare显示点云,Geomagic Studio拟合曲面。所有实验均在一台2.90 GHz处理器、8.00 GB内存的计算机上进行。以下曲率精简简称算法1,曲变精简简称算法2。
3.2 铸件精简结果
以铸件点云为实验对象,采用不同比率(75%即去除75%的冗余数据点,85%、90%同理)精简,结果如表1、2所示。
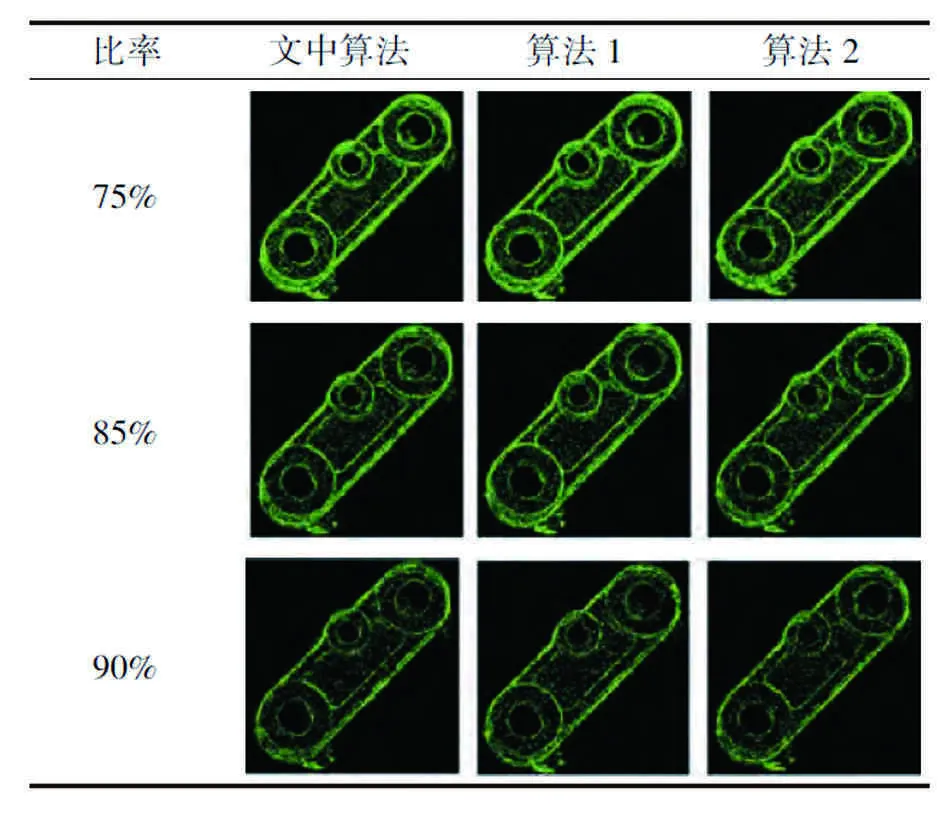
表1 不同精简比铸件点云数据
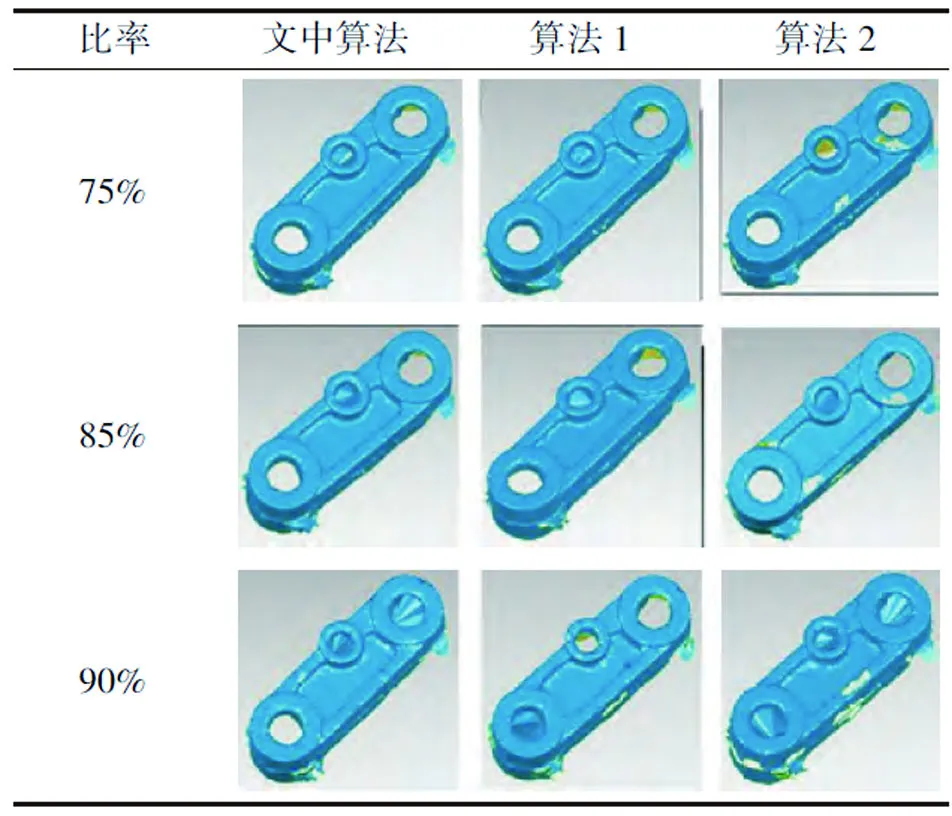
表2 铸件曲面重构模型
由表1、2可以看出:在相同的精简比率下,文中算法处理后的点云具有更好的数据还原性,在曲面重构中具有更少的数据空洞,而保形性误差指标也大幅降低,如图5所示。
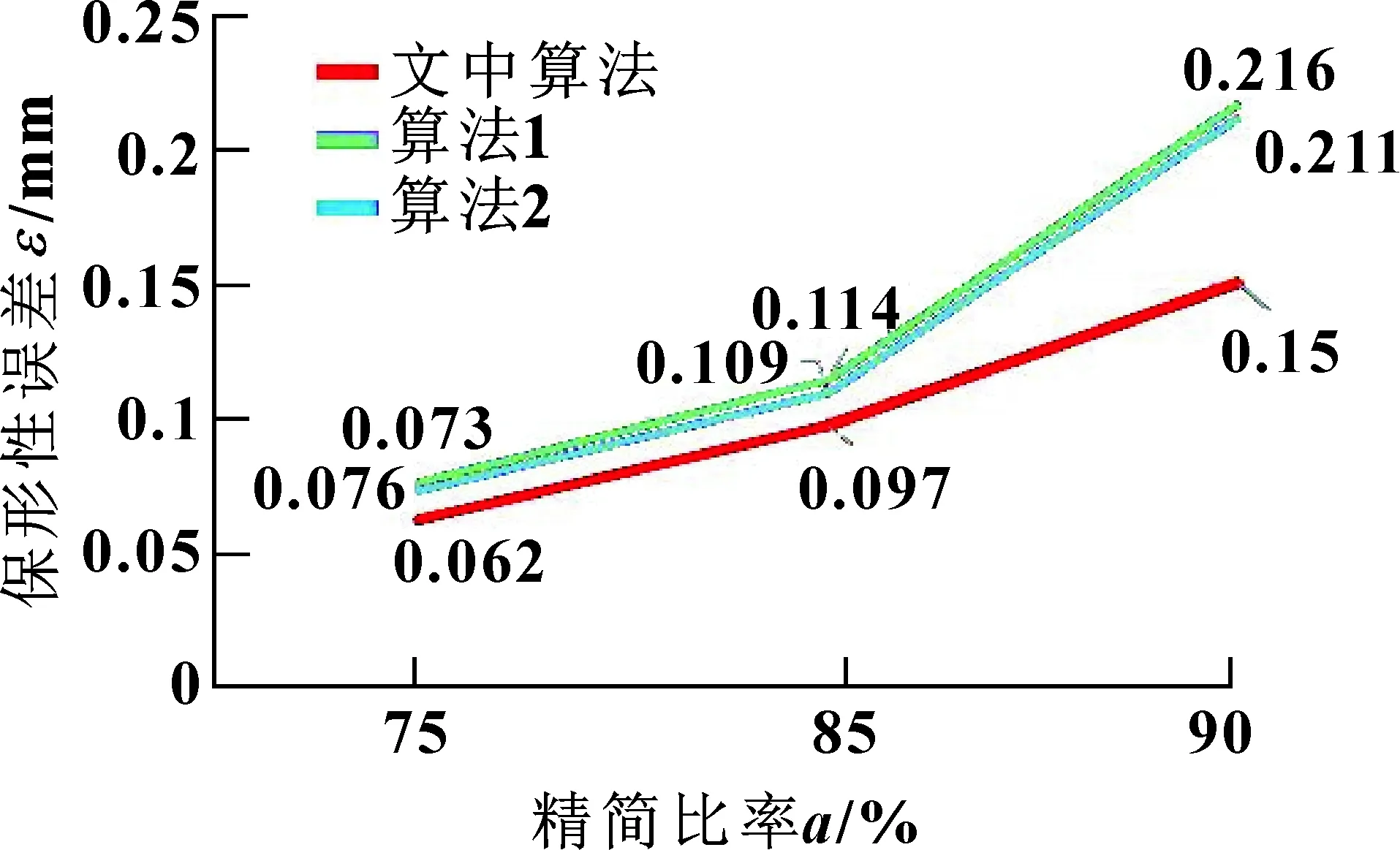
图5 铸件精简点云保形性误差
3.3 Bunny精简结果
为了进一步验证文中算法的鲁棒性,以Bunny模型为对象进行实验,结果如表3、4所示。
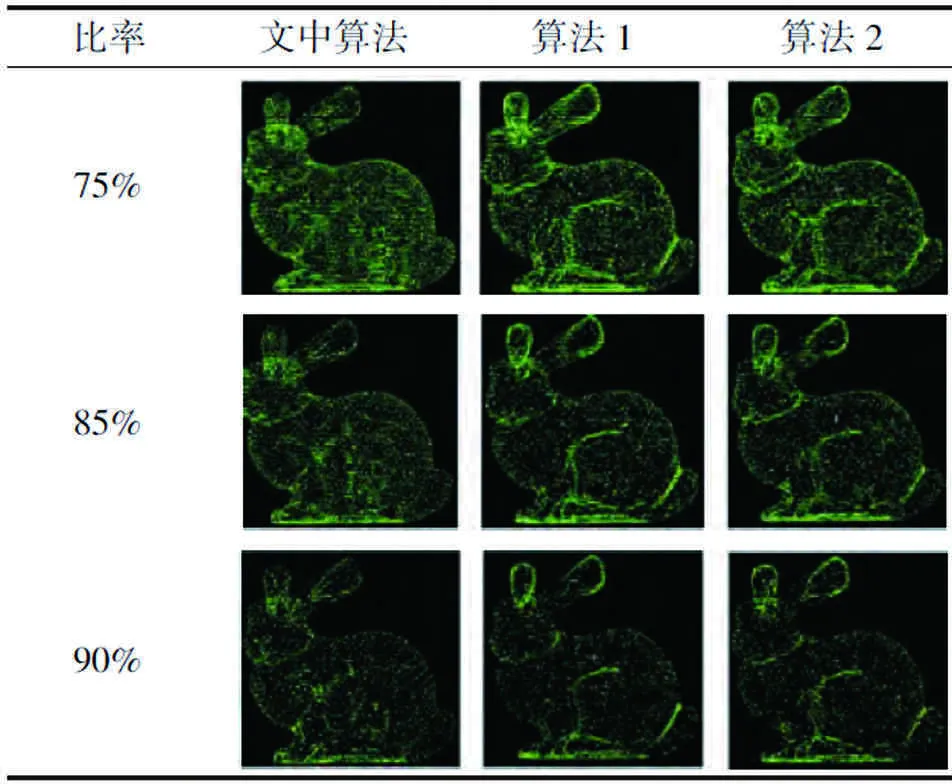
表3 不同精简比点云数据
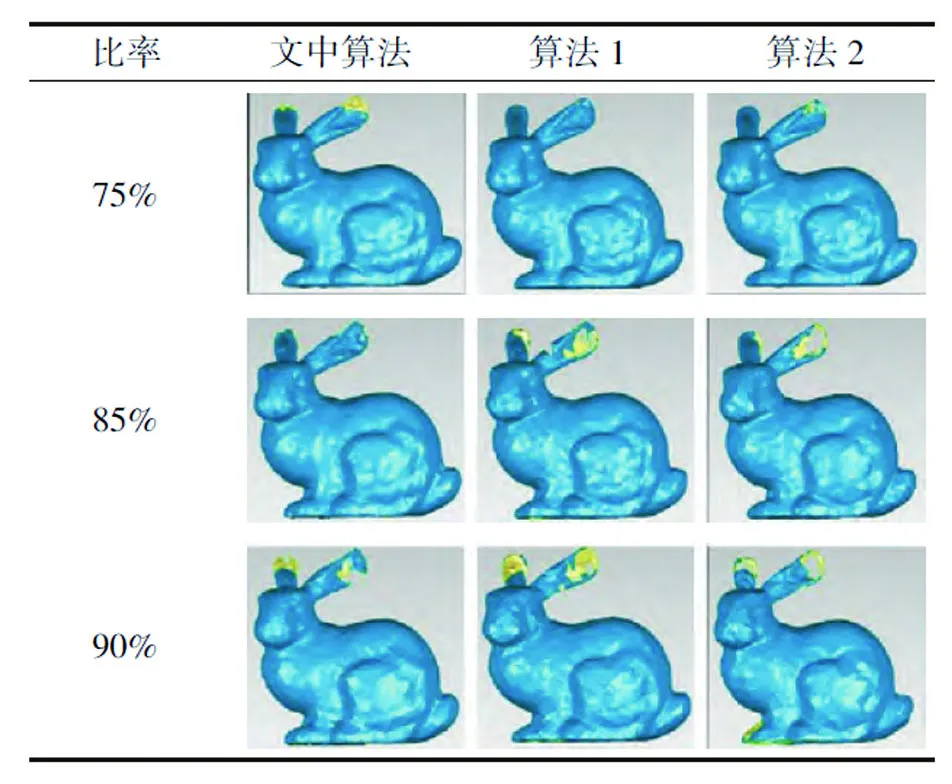
表4 Bunny曲面重构模型
从表3、4中可以看出:当精简率在75%、85%时,文中算法精简点云的重构模型仅有细微的数据空洞,证明该算法具有良好的精简效果;而当精简比达到90%,重构模型在密集点云处(Bunny耳朵)出现部分数据空洞,但仍保存了完整的模型轮廓。这种高精简比适用于计算速度要求高、精度要求相对不高的场合,具有一定的实用性。
从图6中可以看到:相较另2种精简算法,文中精简算法在保形性误差指标上有着明显改善;在精简比75%时误差降低约21%;在精简比85%时误差降低约31%;在精简比90%时误差降低约40%,因此文中精简算法更适用于高精简比场景。
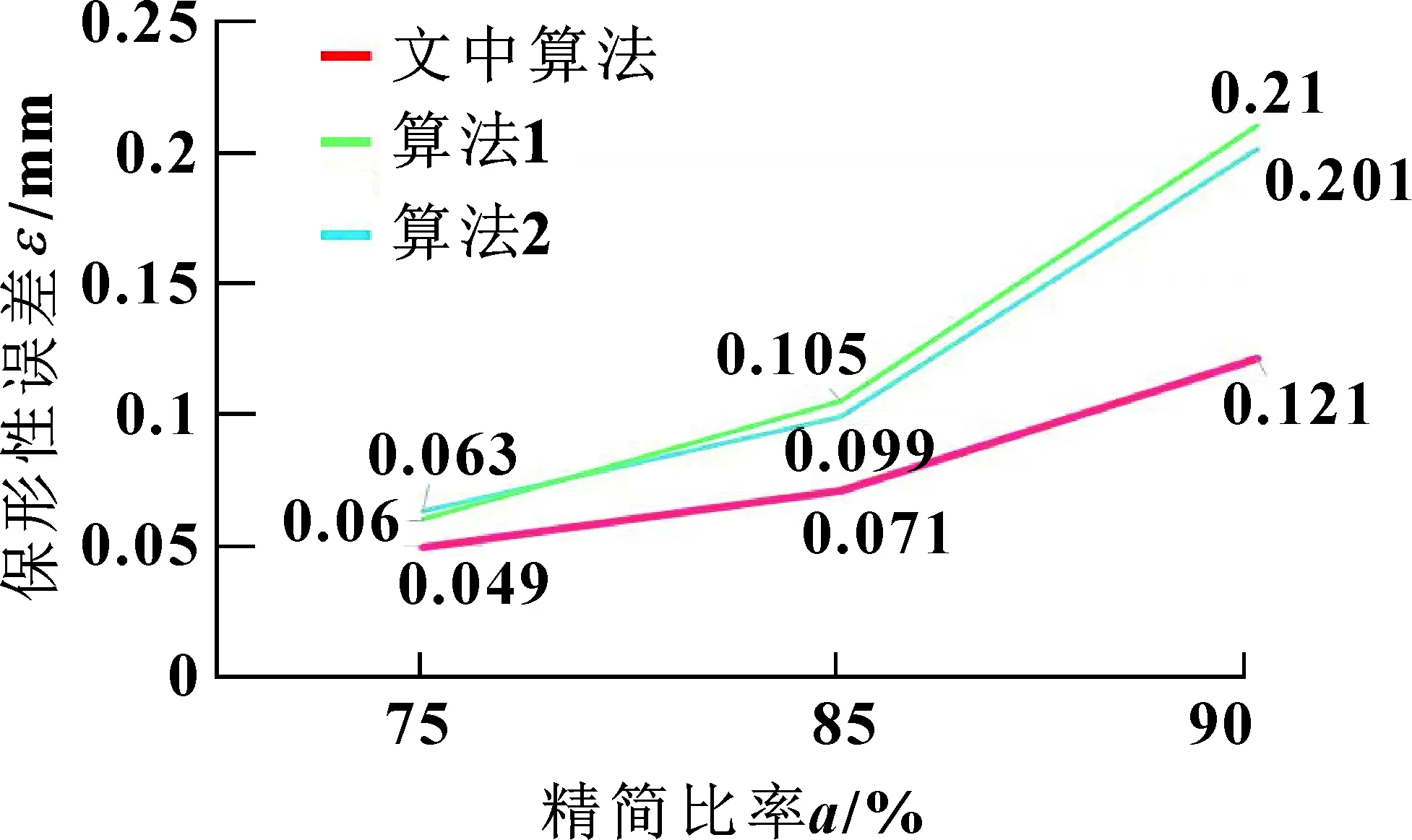
图6 Bunny精简点云保形性误差
3.4 抗噪测试
能否过滤掉由设备误差、操作失误、环境因素等造成的原始点云中的噪声点,也是评判精简算法效果的重要指标。
为了模拟噪声,在Bunny原始模型中加入拉丁超立方1 000点如图7所示,该噪声具有完全的随机性和均匀性。
精简结果如表5、图8所示,从保形性误差、拟合面片数(由精简点云模型生成的重构模型具有的拟合面片数量)进行评判。
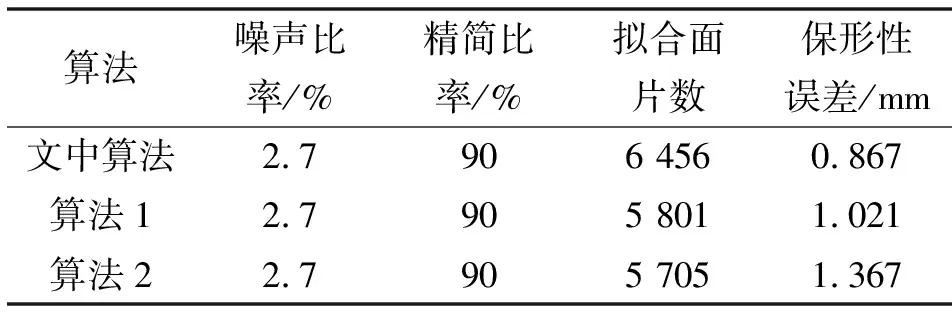
表5 1 000噪声点模型精简数据对比
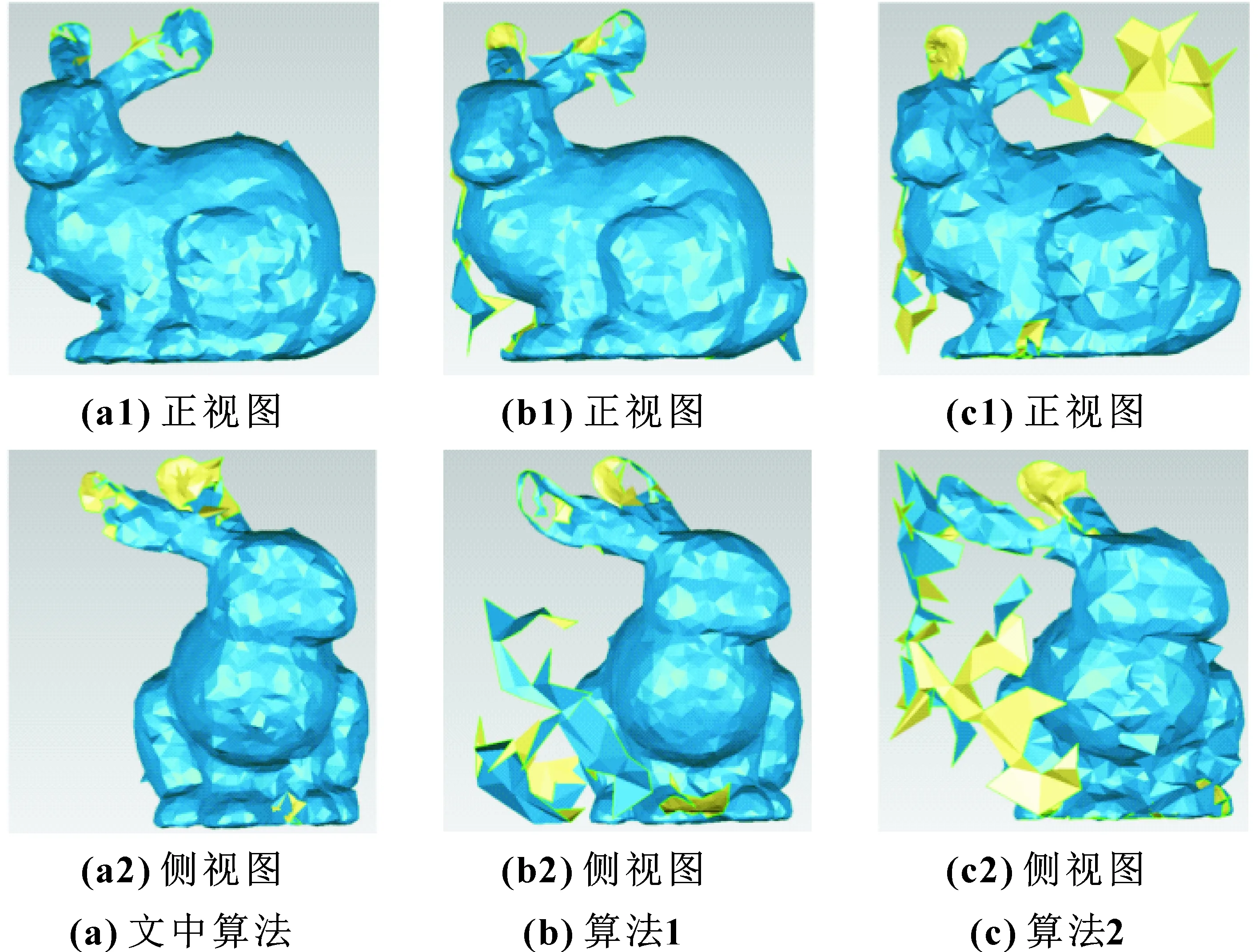
图8 1 000点噪声曲面重构模型
从表5和图8中可以看出:在噪声比2.7%、精简比90%条件下,文中精简算法生成的曲面拟合模型中离散面片更少;同时重构模型中面片数相对算法1、算法2增加了11.2%、13.2%;保形性误差分别降低了15.1%、36.6%。
4 结论
文中提出了一种基于线性耦合曲率的点云精简方法。实验结果表明:
(1)文中方法可在高效剔除冗余点的条件下保留模型原有特征,以便更好地适应后续计算任务。
(2)相较传统曲率精简,文中方法保形性误差降低40%(铸件点云,90%精简率)。
(3)在增加拉丁超立方噪声情况下,文中方法相较传统曲率方法保形性误差降低15.1%,拟合面片生成增加11.2%,证明文中算法在点云数据预处理中有更好的应用。
