阀套开槽对二维阀空化噪声的抑制

赵永华，阮健，唐普洪，岳玉环，赵云

(1.浙江工业大学机械工程学院，浙江杭州 310014；2.嘉兴职业技术学院，浙江嘉兴 314036)

0 前言

二维阀将先导级和功率级集成在一个阀芯的2个运动自由度上，先导级的旋转滑阀开口具有很高的压力增益，电-机械转换器只需输出很小的角位移就能引起压力急剧变化，易于实现阀的快速工作和高频响应。二维阀具有体积小、性能稳定、动态特性理想、抗污染能力强、泄漏流量小以及功重比大等优点。二维阀阀芯的转动使得阀的节流口频繁启闭，通过节流口的液体压力骤降，当液体局部压力低于其饱和蒸气压时，液体中原有的“气核”成长为气泡，而气泡在高压处溃灭，就会发生空化[1]。空化现象是引起二维阀压力脉动、振动和噪声的重要原因[2]。

很多国内外学者从阀的结构参数着手，对阀内空化的发生、空化强度及抑制等做了研究。杜学文等[3]研究了节流槽结构特征对阀内压力分布、气穴与噪声特性的影响，得出U形槽比V形槽更能抑制气穴的析出与生长的结论。OGAWA和HISADA[4]发现在蝶阀中，当沟槽深度是导管高度的1/5且沟槽的长度等于导管的高度时，阀门中的空化噪声可以最大程度被降低，同时改变沟槽的形状还能减轻二次空化噪声。旋转阀的空化强度随着入口口径的减小而增加，为抑制阀中空化的发生，阀门的槽深需要选取适当[5]。采用倒圆、适当的密封锥角以及倒锥孔可以使控制阀阀门有更好的抗空化性能[6]。FENG等[7]发现在弧形阀门中，出口顶部倾斜角应该减小，并且当横向偏移宽度较小时应该缩短其水平长度从而减轻空化强度。KIM等[8]发现改变排气阀中的弹簧常数可以预防阀门中空化的发生，而改变恒压阀中的流量以及弹簧常数也可以起到同样的效果。XU和XUAN[9]发现在船闸阀中，可以在阀门后增加突扩涵管减轻阀门中空化发生的可能性。

在实验研究中，声学法(空化噪声法)由于精度高，噪声信号可以直接转变成电信号，并通过专用的处理系统，可以很好地得到声压和声能的曲线，从而可以直观地分析和判断，所以该方法成为目前较为理想的空化实验方式。鉴于实验条件的限制，加上空化现象影响因素的复杂性和多样性，很多空化实验通过数值模拟的方式完成，并且模拟的结果与实验吻合良好。

大涡模拟(Large Eddy Simulation，LES)是空化噪声数值模拟中使用最多的方法之一。MOIN[10]使用LES方法研究了BLAKE[11]实验研究的随边诱导噪声问题，在表面压力脉动、速度统计值及远场噪声级上均能与BLAKE的实验结果合理吻合。WANG 等[12]应用LES方法研究风扇叶片流场脉动压力的时间变化。BOGEY等[13]利用LES方法模拟雷诺数为6.5×104、马赫数为0.9的射流噪声，同时进行了实验验证。BOGEY和BAILLY[14]利用LES方法预报射流噪声的实用性，计算了一系列马赫数、雷诺数条件下热射流和冷射流的声辐射，计算结果与实验总体吻合。张允等人[15]基于LES和Lighthill声比拟方法，对开孔潜艇流噪声进行了数值模拟，计算结果与实验结果吻合良好。

基于以上所述的研究方法，本文作者以二维阀先导级结构为研究对象，利用Fluent软件进行数值模拟，对比研究不同阀套结构下阀内流场的流速变化、压力分布、气体体积分数等流动特征，进而分析监测点的噪声频谱，为二维阀的结构优化提供理论依据。

1 二维阀的工作原理

二维阀的工作原理如图1(a)所示。图1(b)所示的电-机械转换器(力矩马达)将控制器的电信号转换为机械信号，并传递给机械传动机构。转动信号通过传动机构按比例放大驱动力矩从而带动阀芯旋转，阀芯的旋转使得阀套斜槽与高低压口的重合面积发生变化，阀芯左端的敏感腔压力随之变化。敏感腔压力的变化造成阀芯两端的压力失衡，从而驱动阀芯轴向运动，以控制阀的压力和流量输出。

图1 二维阀工作原理(a)及结构(b)

2 仿真模拟前处理

2.1 流道模型建立

利用UG软件建立三通径二维阀的三维模型，如图 2(a)所示。反向建模生成流道模型，二维阀先导级阀口通道结构具有双流道中心对称的特点，如图 2(b)所示。当阀芯旋转打开高压节流口时，流体经过主阀芯中间孔的流道流至如图3(b)所示模型的入口，经过渡通道到达高压区，经高压节流孔至阀套斜槽内，再流至敏感腔。文中选取一半的流体模型作为分析对象，如图3(b)所示。进口流道直径为2 mm，过渡流道直径为1.2 mm，出口处的面积约为4.5 mm2。

文中设计了在阀套斜槽两侧面开U形槽的抑制空化的结构。考虑到二维阀的结构特性及功能要求，开槽阀套的结构及槽的位置如图3(a)所示。图3(c)所示为此研究所取的阀套开槽后的流体模型。

图2 二维阀模型(a)及其流体模型(b)

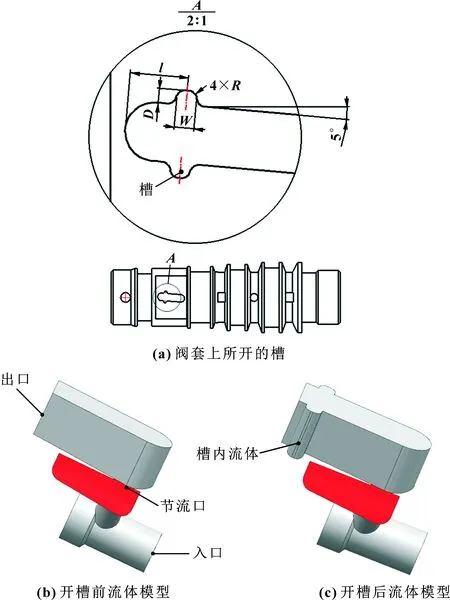
图3 开槽阀套及流体模型

2.2 网格划分及网格无关性检验

使用Mesh软件进行网格划分，如图4所示，采用四面体网格，对滑移面和节流口进行局部加密处理[16]，使计算结果更加精确。

得到网格数量为223 568，在一个计算周期内，阀芯对称面平均压力值变化在1%以内[17-18]，满足网格无关性要求，如表1所示。

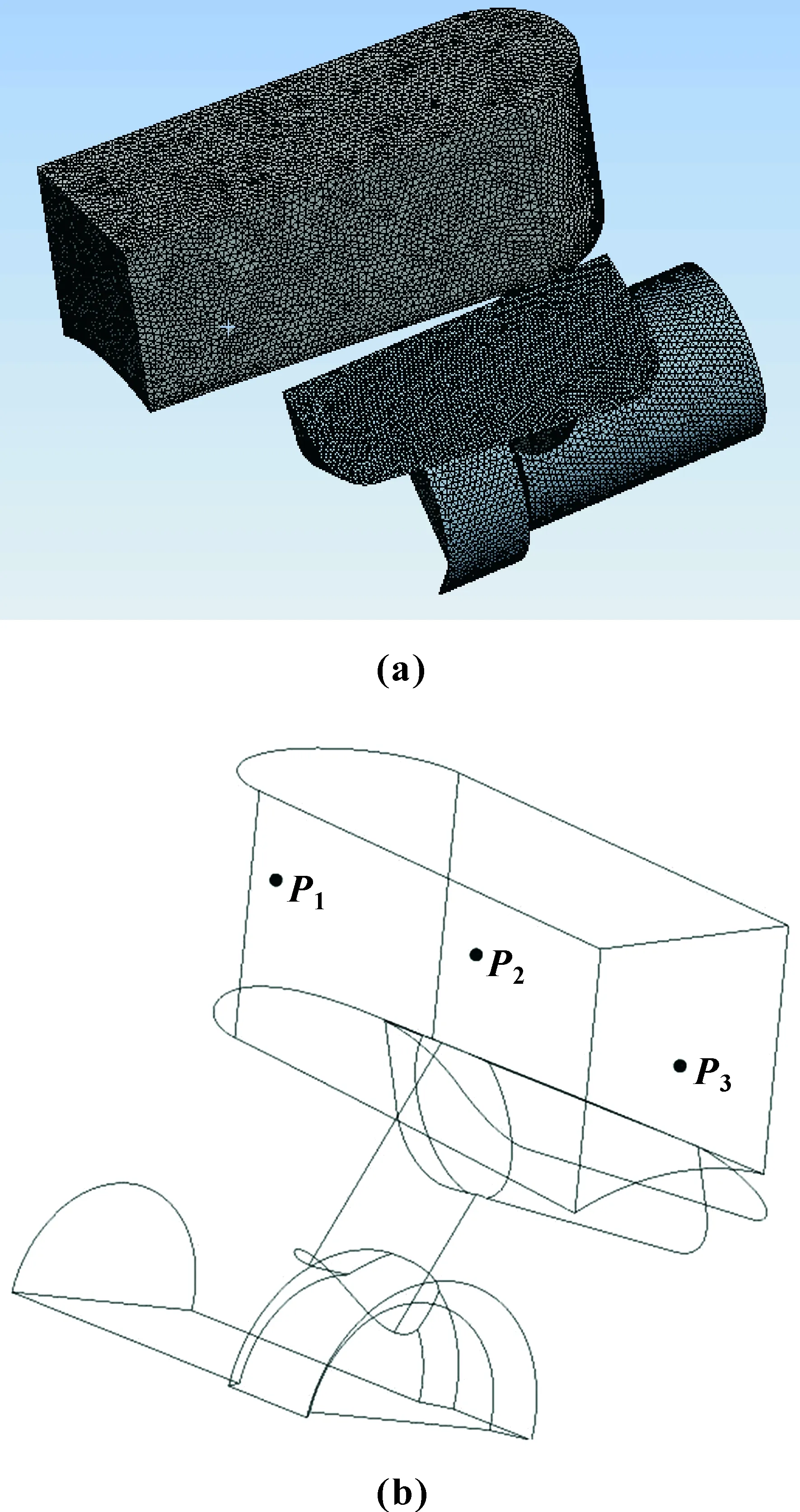
图4 模型网格(a)及监测点(b)

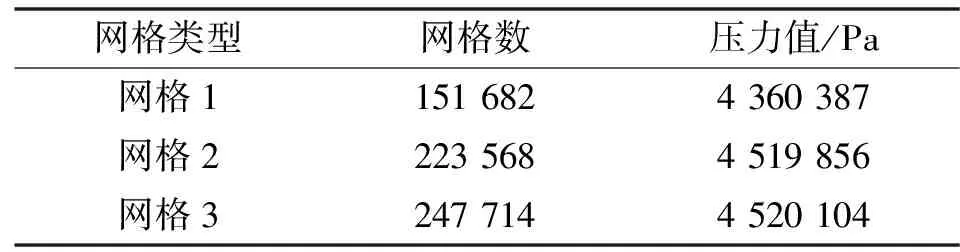
表1 网格无关性检验

3 计算方法及边界条件

3.1 大涡模拟控制方程

LES模型的控制方程是基于Navier-Stokes方程，去掉比过滤宽度或给定物理宽度小的涡旋得到的。控制方程[19]为

(1)

(2)

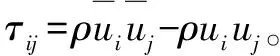
3.2 Schnerr-Sauer空化模型

Schnerr-Sauer空化模型没有引入任何的经验系数，模型描述为

(3)

(4)

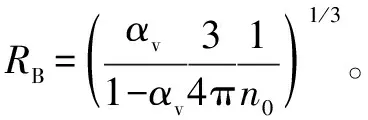
式中：RB为空泡半径；pv为流体的饱和蒸气压力，取20 ℃时油的饱和蒸气压力pv=37 100 Pa；n0为单位液体体积空泡数密度，模型中取n0=1013。

eID芯片DS2431的页读操作与页写操作类似，不过只需一个步骤，通过发送“Read Memory”命令，读取相应页地址内的数据。

3.3 噪声模型

Fluent中采用FFOWCS WILLIAMS和HAWKINGS提出的FW-H方程模拟声音的产生和传播，具体形式为

(5)

式中：Tij是Lighthill应力张量；H(f)是亥维塞德函数；δ(f)是狄拉克函数；c0为当地声速；P′为声压。式(5)中等号右边的3项分别表示单极子声源、偶极子声源和四极子声源。

3.4 边界条件

利用Fluent对二维阀先导级的流场和声场进行数值模拟，采用混合多相流模式的空化模型和大涡模拟模型，选择PISO！压力速度耦合算法，一阶迎风格式进行计算。定义主相为液压油，密度780 kg/m3，黏度0.002 4 kg/m·s；次相为空气，密度1.225 kg/m3，黏度1.789×10-5kg/m·s，主相与次相的转换满足Cavitation模型。数值模拟采用压力入口(pin=7 MPa)、压力出口(pout=0.1 MPa)以及无滑移标准壁面函数边界条件。

根据奈奎斯特采样定理：

t=1/2f

(6)

综合考虑计算时间和计算结果精度，设置分析时间步长t=0.000 5 s，计算2 400步，得到频率f为0～1 000 Hz的频谱。

4 仿真结果分析

基于上述数值模拟的设定，在Fluent 2020R2中对模型仿真计算。选取阀芯节流口开度为0.01 mm，对比原斜槽结构和斜槽两侧壁面开宽深比(W/D)为2.2的U形槽，分析二维阀先导级内流场的空化特性、流动特性及噪声频谱。图5所示的研究面分别为：主分析面(z=2.522 263 05 mm)、分析面1(z=4.522 263 05 mm)、分析面2(z=6.522 263 05 mm)、分析面3(x=-0.886 833 377 mm)和斜槽底面(y=3.879 218 915 mm)。

空化数被广泛用于表征空化强度或空化的发生。流经液压阀节流口的空化数σ[20]定义为

σ=2(pl-pv)/(ρv2)

(7)

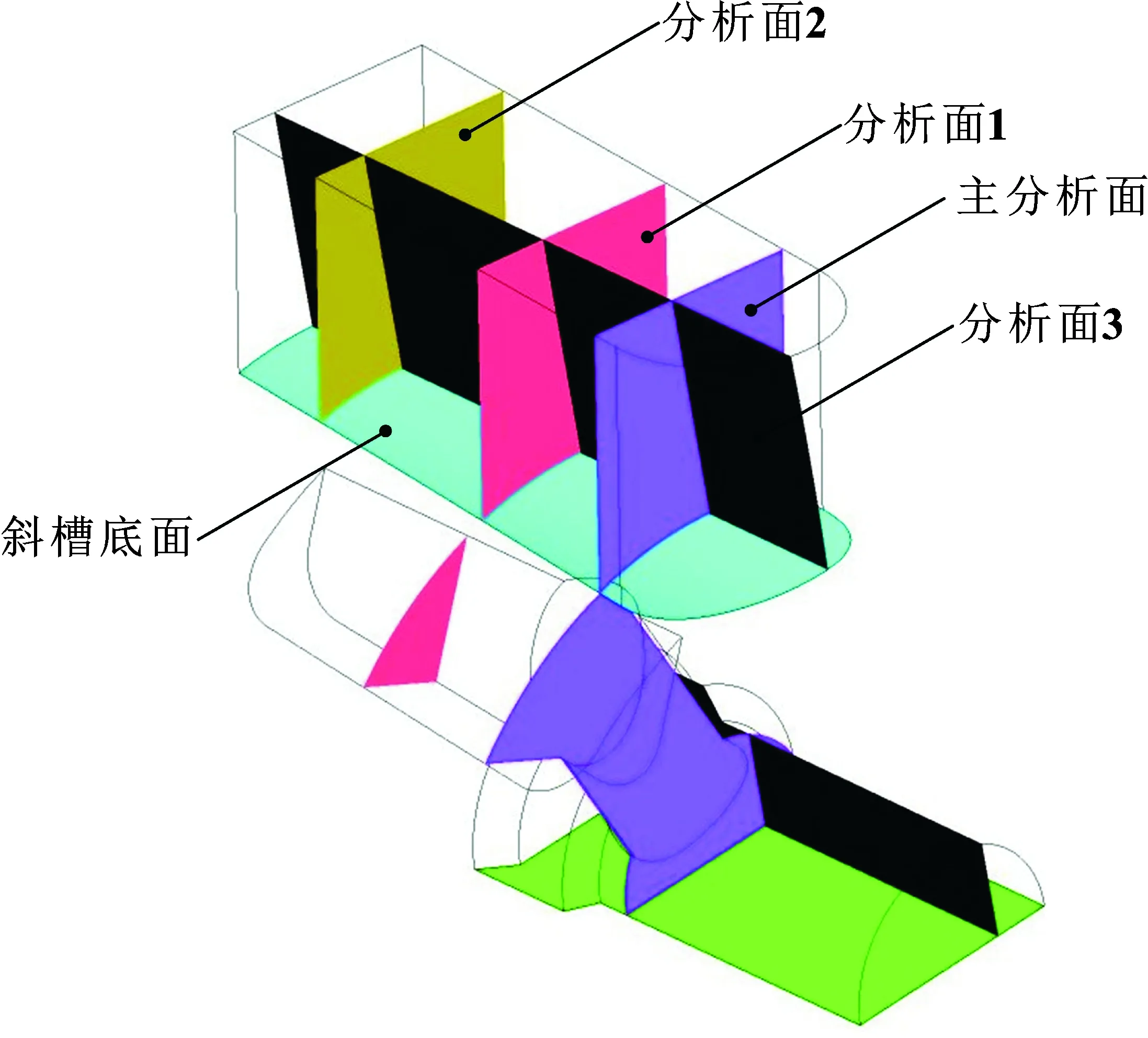
图5 模型研究面位置

4.1 空化特性

图6所示为主分析面上的速度分布。流体经过节流口后，在下游的阀套斜槽区形成了高速射流，节流口上下游的压降使得斜槽区出现负压，气穴形成。原结构的速度最大值比开U形槽结构的略高。

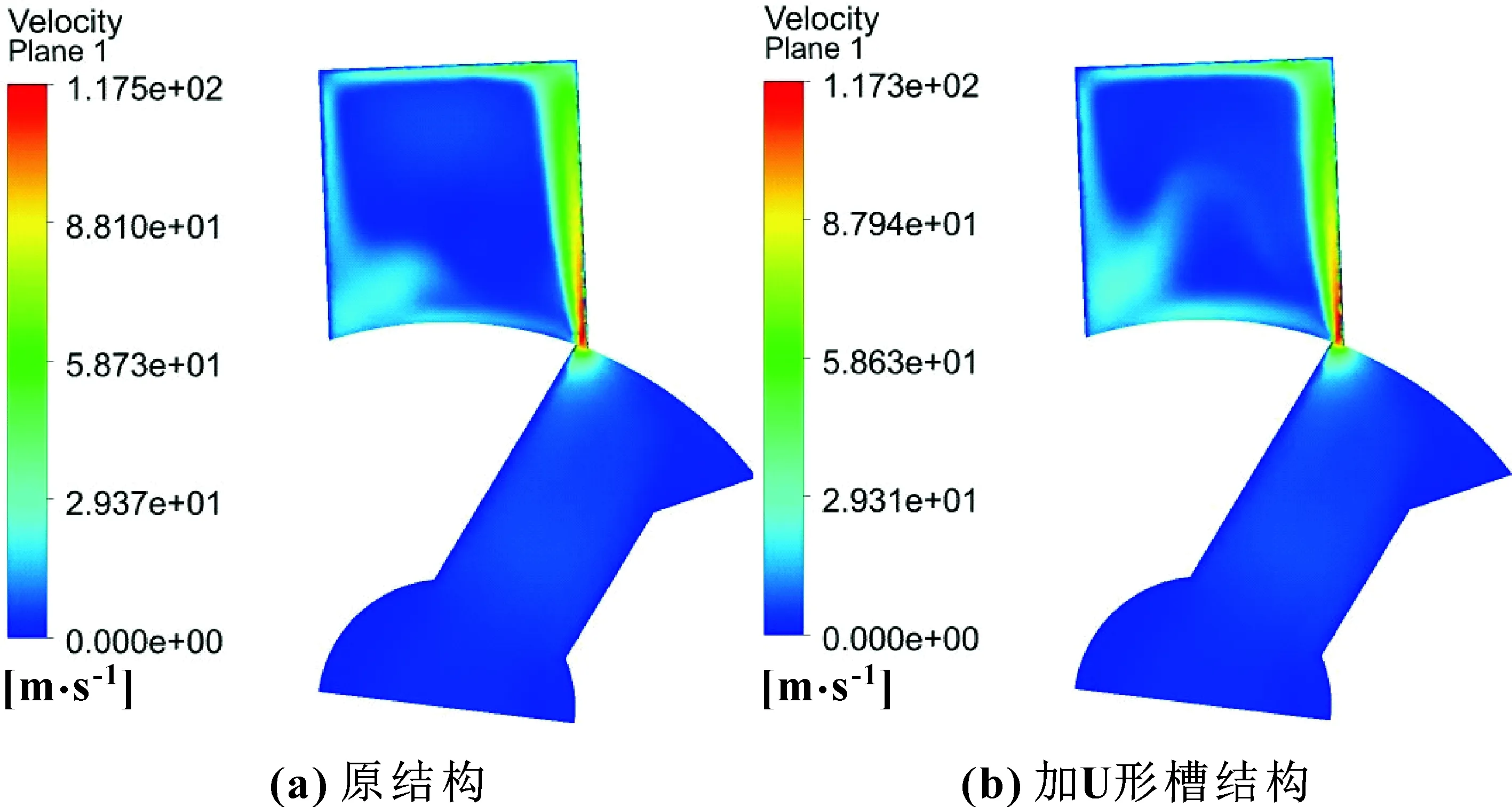
图6 主分析面速度分布

图7所示为斜槽底面的压力分布。因节流口的节流作用，开U形槽后斜槽区底面的压力最大值增大了0.04 MPa，且沿着流体流动的Z方向压力值变化程度减小，由原结构的0.025 MPa提高到了0.1 MPa，说明开U形槽后，斜槽区的空化程度有所减弱。

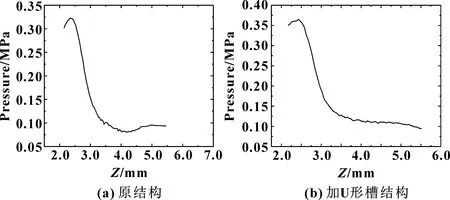
图7 斜槽底面的压力分布

图8显示了2种结构斜槽区气体体积分数为0.000 1时的分布。可以看出：原结构在节流口处的气体体积要大于开U形槽后结构的气体体积。

图8 斜槽区气体体积分数为0.000 1时的分布

从图9所示的斜槽底面速度矢量分布可以看到：开U形槽结构与原结构相比，U形槽中有向槽里侧的径向速度，阻碍了出口方向沿流出方向的流线分布，且流速越大，这一径向速度也越大，降低了气泡进入敏感腔的概率，大大减少了气泡在高压处溃灭的可能，有效地降低了斜槽内空化的程度。

图4设置的3个监测点P1、P2、P3分别位于阀套斜槽的后部、中部(离节流口最近)以及出口处，从图10所示的监测点空化数对比曲线可以看出：在斜槽后部，2种结构的空化程度相当，在节流口附近原结构的空化程度要高于开U形槽结构，原结构在出口处，整个时程的空化数要低于开U形槽结构。

4.2 流动特征

图11所示为原斜槽结构与开U形槽斜槽结构在图5所示分析面上的流线分布。原结构斜槽区与流动方向垂直的3个分析面中，在节流口位置处的主分析面上，受节流口高速射流的影响开始出现流动导向的中心漩涡雏形，到分析面2时，导向涡中心密度增加，且随着阀口开度加大，漩涡逐渐向斜槽外侧壁靠近；距离出口最近的分析面3上的流线显示，导向涡中心密度降低，壁面流线密度增加，说明原结构斜槽中心的横向流动涡涡结构虽然保留，但流势渐弱。3个分析面均无明显的自由剪切涡流动，斜槽内壁面附近也无明显的漩涡结构。如图11(d)所示，随着阀口开度的增大，多漩涡汇集形成了切向的大漩涡，但并没有影响主流流线的变化，说明涡旋对主流的影响比较弱。

斜槽两侧壁开U形槽后，节流口上游的流线与原结构基本一致，斜槽底面的流线，除了U形槽中流线外，其余的流线流态也没有变化，说明U形槽结构不影响阀芯中的流体流态，对滑移面的流态也无大的影响。但斜槽两侧壁开U形槽后，对节流口下游区域的流体流动影响巨大。从4个分析面的流线可以看出：与流动方向垂直的3个横向切面上，横向的二次流动十分显著，切向的涡结构完全主导了斜槽区的流动。从主分析面到分析面1，导向涡非但没有减弱，涡的中心密度反而更大，且强势占据斜槽区的中心位置；到了分析面3，由于U形槽的分流，U形槽内出现了能量较弱的数个小涡旋，但导向涡的中心位置不变，且涡心能量依然很强，斜槽区内存在强烈的横向漩涡流动，大大削弱了主流势能。从流向切面的另一个角度看，节流口出流之后，斜槽区后部形成了数个涡结构，受U形槽的影响，距离出口很近的位置出现了封闭的小涡，涡结构控制了主流流动。

通过对比分析面的流线可以看出：开U形槽后，阀套斜槽内的主流势能受到了很大程度的削弱，在斜槽的后部有明显的空化剪切涡，但在主流方向上未见自由剪切流动，与原结构的流动行为存在比较大的差异。原结构的流动显示，主流流线比较连续，横向二次流动较弱，斜槽内主流流向一致性较强，切向涡受主流流动影响，有较大的涡形变化。

4.3 噪声及频谱

图12所示为3个监测点声压级的对比。可知：开U形槽后，监测点P1和P3的声压级比原结构降低了3～10 dB，监测点P2的声压级高出2 dB。

图13所示为原结构监测点功率谱密度。可以看出：点P1的噪声频谱集中在100 Hz内，是典型的空化噪声频率，在200 Hz处出现了一个噪声次频。点P2在低频区的频谱密度低于点P1，但声压频率分布要比点P1宽，频率延伸到了300 Hz。点P3频谱密度也在低频区，频率密度集中在180 Hz以内。

图14所示为开U形槽结构监测点功率谱密度。可以看出：点P1的噪声频谱集中在100 Hz内，比原结构在该点的频宽还要窄。与原结构相比，点P2的主频在20 Hz，次频宽度延伸，在180、230、280、400 Hz均出现了明显的次频。与原结构相比，点P3的主频在低频，且频宽收窄在100 Hz以内。

图12 监测点声压级对比

图13 原结构监测点功率谱密度

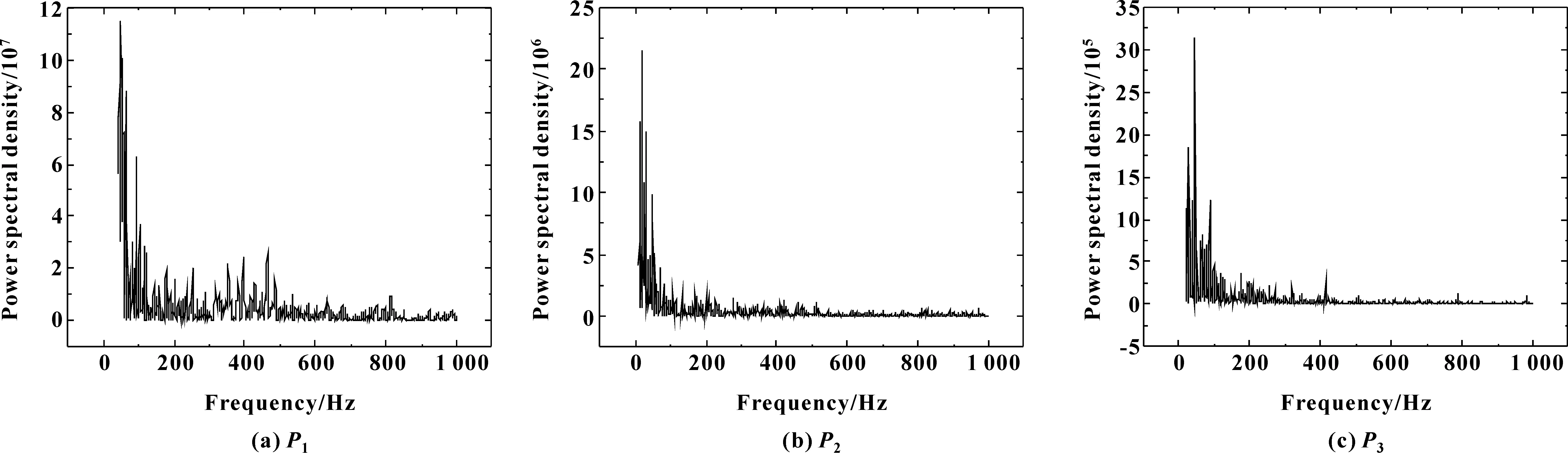
图14 开U形槽结构监测点功率谱密度

5 结论

通过对比不同结构在主分析面和斜槽底面的流动特征，发现在阀套斜槽两侧面开U形槽后，阀套斜槽内的空化有所减弱，表现为主分析面的射流速度有所降低，斜槽底面的气体体积分数下降。这说明斜槽两侧开U形槽后，改变了阀套斜槽内的速度流线，削弱了高速射流流体剪切流动的效果，从一定程度上减弱了空化噪声。通过进一步分析阀套斜槽内所设监测点的噪声频谱，结果表明：阀套斜槽两侧面开U形槽结构与原结构相比，在斜槽区空化最严重的后部，噪声降低了10 dB，在模型出口处，噪声降低了3 dB，在斜槽中部，噪声声压级略有增加，增加幅度为2 dB。说明在阀套斜槽两侧面开宽深比为2.2的U形槽确实能降低二维阀先导级因空化引起的噪声。