基于FEM的超高压液压顶升装置力学特性分析

赵映辉，陈雪林，刘安民

(1.衡阳华菱钢管有限公司，湖南衡阳 421001；2.东北大学材料科学与工程学院，辽宁沈阳110819；3.中南林业科技大学机电工程学院，湖南长沙 410004；4.湖南工学院汽车泵类零件设计制造技术国家重点实验室，湖南衡阳 421002)

0 前言

液压系统广泛应用于各行业中力或位移的控制，由于液压系统的非线性，非线性约束对系统的力学特性影响较大，振动使得摩擦力与摩擦因数耦合作用，使得摩擦力表现为非线性，系统弹性恢复表现为分段非线性，液压系统等效刚度随振动表现出弱非线性，使其较难获得能准确预测或者评估高频率往复运动精度的有效预测模型[1-3]，尤其在超高压液压密封装置中。一个重要原因就是，在超高压工况下，液压密封元件产生了能够显著影响密封件密封性能的变形与应力集中[4-5]，导致了润滑性质的变化[6-7]、运动表面性质被破坏[8-9]、液压缸位置难以精确控制[10]等问题，使得对超高压密封结构中关键零部件的强度、刚度提出更高的要求，但国内的主要研究集中在液压系统线性与非线性控制、动态特性、油液对系统传动的动态性能等方面[11-15]。液压缸的动态特性与控制、结构参数密切相关，较多研究集中在阀、液压缸的流量特性和负载特性分析，液压缸在定值或突变负载下的压力、流量和活塞位移的变化规律[16-17]。也有研究集中在液压缸低速爬行中摩擦自激本质特性与数学模型[18]，液压系统弹簧刚度和摩擦力等非线性因素对液压缸动态特性的影响[19]，液压弹簧刚度数学模型[20]，新型半圆圆柱形液压缸的设计[21-22]等方面。刘飞等人[20]分析了非线性约束下液压缸的力学及频率特性，结果表明系统振动不稳定区域随弹性力而增大。彭欢等人[22]分析了振动对液压缸动态特性的影响，结果表明压力波动幅值与基础振动幅值成线性相关，为液压缸的结构参数优化提供理论依据。针对液压缸在超高压下工况的力学分析较为少见，李晓东[23]采用有限元法对液压缸进行了静态、动态力学分析，结果表明液压缸变形对其性能影响较大，引起内泄漏、颤振，减少了液压缸使用寿命。杨秀萍等[24]采用有限元法对液压机及液压缸进行了力学分析，优化了设计方案并验证了结果的可靠性。张卫国等[25]测量了工作中液压缸的压力、位移等参数变化曲线，并对液压缸进行了有限元计算与实验验证，其结果表明有限元计算结果与试验结果基本一致，有限元分析结果为液压顶升装置结构设计提供了建议。TORBACKI[26]采用有限元法对液压缸进行了力学分析，结果表明液压缸的使用工况对其力学行为影响较大。MACKERLE[27]对采用有限元法分析不同载荷下连接结合面的文献进行了总结，有些集中分析结合面静力学行为，有些集中于动态阻尼特性[29-30]，有限元法能够适用于结合面的分析。较低压力下，液压缸的力学行为对密封性能的影响较少，但超高压工况对结合面结构要求较高，液压缸微小的力学行为变化都会对密封性能产生重要影响。林峰等人[2]分析了超高压液压技术在重型模锻液压机方面的应用，超高压液压技术难题的成功解决，使得与液压机相关的设备质量迅速降低，对提高我国基础装备制造能力与工业技术水平至关重要。对于超高压液压结构的密封性能对结构的力学特性行为较为敏感的系统来说，超高压液压顶升装置关键零部件的力学特性微小的变化对其密封性能产生关键影响且有利于其轻量化设计。本文作者分析了液压顶升装置在不同的极限工况下、不同因素对其力学特性的影响，为液压顶升装置结构设计、超高压液压密封结构及匹配参数与使用性能提高方法提供了依据。

1 有限元模型

1.1 模型的描述

文中模型数据均来源于超高压液压设备及配件供应商。液压顶升装置的结构、三维模型、网格划分模型[31]分别如图1(a)(b)(c)所示。其中液压顶升装置主要由底板、液压缸、外套、活塞杆构成。三维模型包括地面、底板、液压缸、外套及地面。由于在超高压液压顶升装置中，活塞杆的压缩变形对密封性能的影响较小[3]，文中不分析活塞杆的力学特性。

材料属性如表1所示。由于各种材料的性能参数与其加工工艺密切相关，其性能参数并不统一[19]。

图1 超高压液压顶升装置的CAD模型(a)、三维模型(b)、网格划分模型(c)

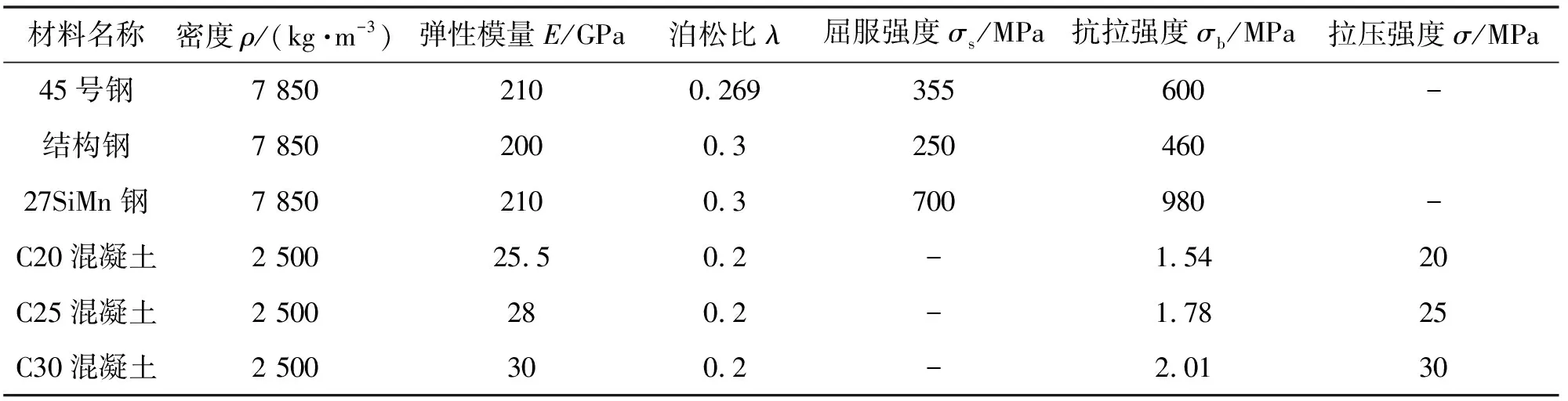
表1 材料的属性表[19，32]

1.2 边界条件

接触方式设置。底板与液压缸、底板与外套、外套与液压缸的连接方式均为螺纹连接或焊接，设置为面-面接触线性连接方式bonded，其接触面各个方向均不产生分离[33-34]。超高压液压顶升装置使用情况决定了地面与底板接触过程中各个位移方向，本文作者考虑以下工况[35]：(1)底板与地面竖直方向无位移、切向微小滑移，设定为No separation；(2)底板与地面法线方向产生位移、切向可滑动，设定为Frictionless；(3)底板与地面竖直方向产生位移、切向不滑动，设定为Rough；(4)底板与地面法向产生分离、切向产生滑动，摩擦因数设定为0.2-0.6[31]，设定为Frictional。

网格划分。采用了Solid93单元[27，29]，并在结合面采用3阶加密网格，设置形状拓扑、变形连续。检查网格质量，包括每个面上单元偏斜度、长宽比、翘曲度、雅克比率，均达到了合理范围[35-36]。整个模型划分为126万网格单元，187.9万左右的网格节点。

载荷设定。液压顶升装置极限顶升载荷为5×105N，最大顶升高度为140 mm。液压缸的内、外径分别为80、95 mm，内部工作介质压力为99.5 MPa，属于超高压的范畴[2]。对于具有工作介质承压的部位，文中均设置为面载荷的形式，以静载荷线性加载方式作用在液压缸、底板内部孔径部位，地面底部固定[24-25]。单位统一采用国际标准公制单位，模型的构建与计算均在有限元软件Workbench14.5中完成，设置迭代误差收敛值为0.001，求解液压顶升装置的模态、基频、等效应力、位移及应变。

结果的可靠性。计算前后分别检查了局部网格连续共节点，位移与载荷边界的加载点是否在模型上，位移连续性，位移与力的幅值，均在合理范围内[35-36]。

2 压力试验验证

试验验证在液压测试平台上开展，采用东华DH5922N动态信号测试系统采集信号，应变片为中航工业电测仪器股份有限公司制造，其型号为BE120-3AA(11)，如图2所示。液压缸内径为75 mm，外径为85 mm，材料为45号钢。测试位置为一孔侧，该区域的应力值(位置点45 mm)与有限元计算值(有限元模型底板为结构钢)如图3(a)与(b)所示。试验应力值约为-500 MPa，与有限元计算值较为接近。接触设置为Frictional，且摩擦因数为0.6较为符合实际情况。Rough接触方式比实验结果偏小。

图2 压力试验平台

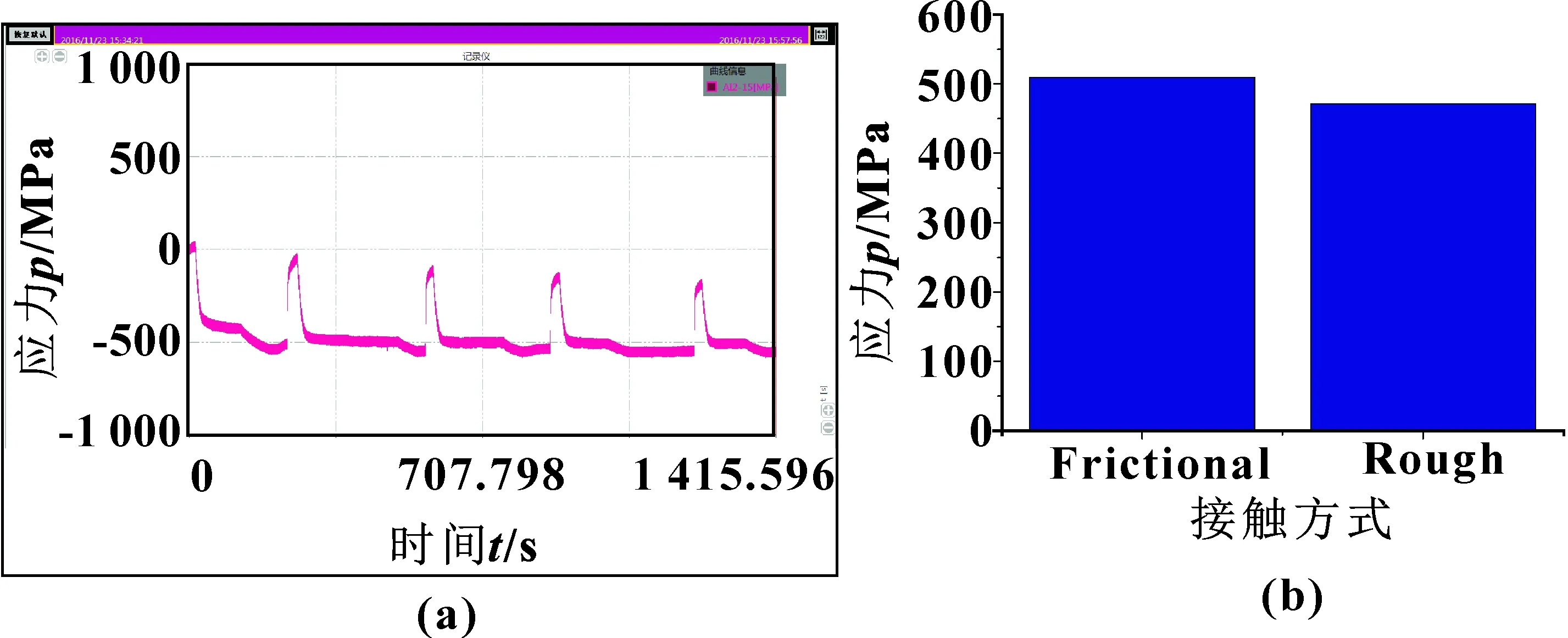
图3 液压缸外侧的应力实验结果(a)与有限元 计算结果(b)

3 结果与分析

3.1 液压弹簧刚度分析

依据文献[14-15]的研究，系统的弹簧力主要来源于受控液压油所构成的液体弹簧。液压刚度等效为液压油的刚度。液压系统采用HM-32液压油[17]。液压缸内外部泄漏引起的附加泄漏流量及总流量-压力系数的增大在文献[12]中已有详细的讨论，液压顶升过程中内外泄漏可以忽略[17]。按照王林鸿等[13]的研究，液压缸的等效刚度可近似表示为位移的函数，如下式所示：

式中：kv为液压油的弹性模量；A1、A2、A3分别为液压缸、进油管道、柱塞泵内径；h1、l1、h2分别为液压缸有效行程、进油管道长度、柱塞缸有效行程；a、b、c为工况选择系数。假设工作过程中及柱塞泵周期性往复运动造成的液压油体积变化对液压力学特性的影响为0，且没有泄漏，这与柏艳红等[16]研究假设一致。柱塞泵到液压缸之间管道距离l1为130 mm，柱塞直径d为20 mm，工作行程为30 mm。

振幅x为0时，液压缸内径为75、80、90 mm的液压系统液体弹簧刚度如图4所示。液压弹簧刚度随液压缸内径尺寸增大而增大，二阶拟合函数方程为Y=13.3+0.196 6X+0.008 6X2。液压系统等效刚度随液压缸内径增大而增大，极限液压弹簧刚度越大。改变其他参数，如管道长度、柱塞泵内径，由于液压缸内径较大，难以显著提升液压系统等效刚度。可通过改变液压缸内径提升液压系统的刚度，改善液压缸的稳定性与应力状态。图5中，随振幅增加，液压系统弹簧刚度显著下降。液压缸内径为75、80、90 mm时，其线性拟合斜率分别为-1.033 84、-1.054 16、-1.181 41，如图6所示。液压缸内径较大时，相对较小的振幅对液压系统刚度的影响较小，其影响系数随内径而增大。改变管道的长度与内径可以有效减少振幅对液压系统刚度的影响。

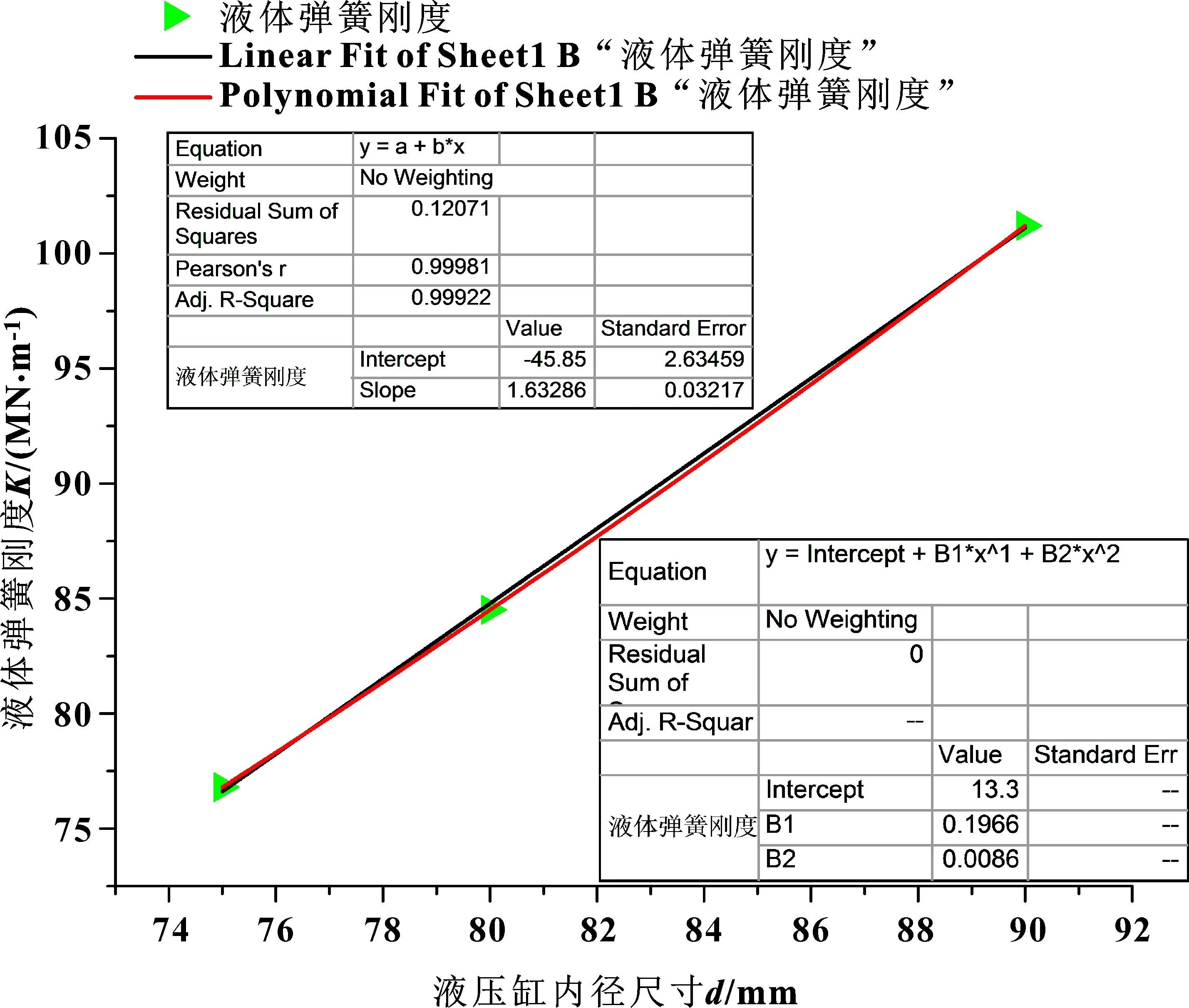
图4 不同液压缸内径尺寸下液压系统弹簧刚度曲线

图5 液压弹簧系统的刚度随振幅变化曲线

3.2 固有频率分析

液压缸材料27SiMn，其余为45号钢，地面与底板接触方式为Frictional，摩擦因数为0.2，其余为Bonded，压力为99.5 MPa。地面材料为C20时，1阶、2阶、3阶固有频率分别为1 578.2、1 582.3、2 536.6 Hz，最大位移分别为24.615、24.667、52.478 mm，如图7所示。尽管结合面螺纹与焊接连接刚度对系统固有频率产生影响，但当地面强度一致时，1、2阶固有频率相差不大，位移也类似，这与文献[28]结论一致。与地面为C20相比，地面为C30时，1、2、3阶固有频率分别减少了3.5%、3.5%、20%，分别为1 523.1、1 526.4、2 012 Hz，1、2阶位移均增加了26%，3阶位移减少了33%，为31.085、31.109、35.28 mm。随着地面强度增加，1、2阶最大位移增加，3、4阶位移快速减少，固有频率降低幅值随阶数增加。

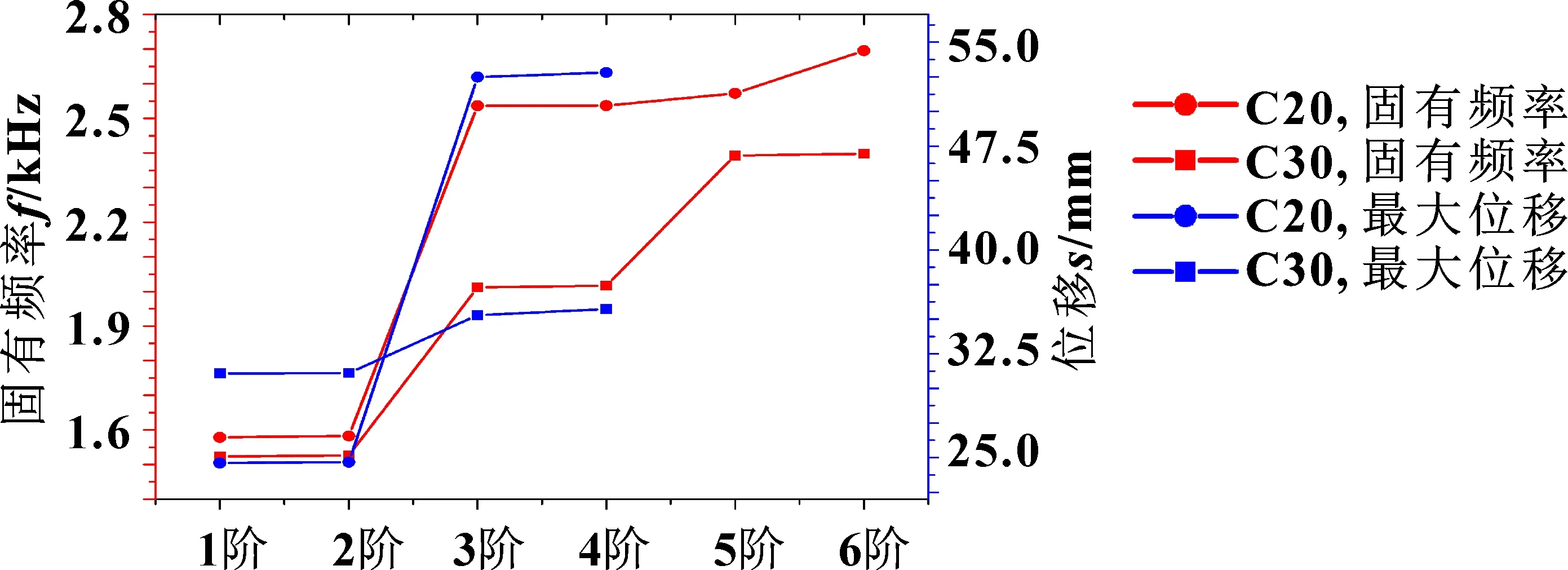
图7 不同阶数下固有频率、位移随着地面强度变化的曲线

3.3 最大应力、应变随接触方式的演变规律分析

液压缸为27SiMn，其余各部件为45号钢时，极限位移随地面强度增加而显著减少，但Bonded接触方式，其最大位移下降的幅值随地面强度增大而快速增加；其他接触方式时，地面强度由C20到C25，与C25到C30相比，位移下降幅值略小。Bonded接触方式最大位移随地面强度增大分别为0.166 71、0.164 31、0.161 12 mm，比其他接触方式极限值中的极小值分别下降了2.97%、3.14%、4.2%，如图8所示，这与文献[22]研究结论一致。这说明，Bonded接触方式下，其效果随地面强度增大而显著增加；其余接触方式，通过增加地面强度的方式减少极限位移的效果随地面强度增加而显著下降。

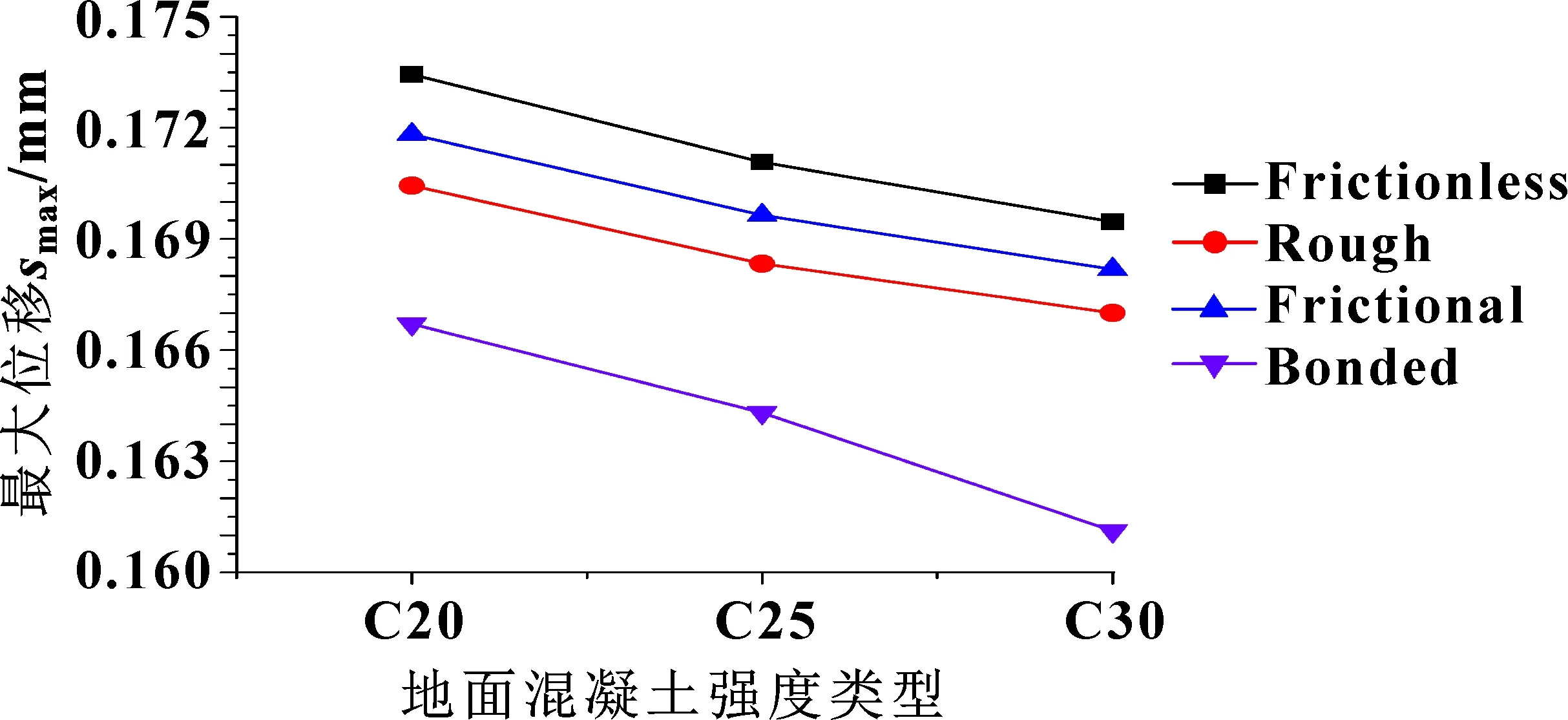
图8 不同接触方式时液压顶升装置最大位移随地面强度的变化曲线

极限应力显示出与之相似的规律，Bonded接触方式极限应力值分别为661.22、657.32、632.12 MPa，与其他接触方式极限值相比分别下降了1.17%、1.74%、5.5%，其他接触方式极限应力值差别较少，如图9所示。这说明，Bonded接触方式能显著减少极限应力值，能降低随地面强度增加而造成的倾斜极限位移的减少。在液压顶升装置中，将底板固定在地面上大幅度减少最大位移与应力，并且随地面强度增加，其效果更加显著，这是由于地面强度的变化导致了底板的位移变化差异，导致了液压顶升装置产生了倾斜[36]。

图9 不同接触方式时液压顶升装置的最大应力随地面强度的变化曲线

图10中，No separation方式接触应变值显著大于其他接触方式，变化规律与其他接触方式不一致。在其他接触方式中，Bonded最小，Frictionless最大，并且随地面强度增加而显著减少。Frictional接触方式下降幅值随地面强度变化显著高于Rough，且存在交点。

图10 不同接触方式时液压顶升装置最大应变随地面强度的变化曲线

3.4 液压装置最大应力、位移与液压缸材料间的影响规律分析

接触方式分别为Frictional、Rough，液压缸材料分别采用结构钢、45号钢、27SiMn时，最大位移、应力随地面强度的变化规律分别如图11与图12所示。液压缸材料为27SiMn时，其最大位移远小于其他材料，且下降幅值随地面强度增加而减少。Rough接触方式中，27SiMn与45号钢相比，最大位移随地面强度变化依次缩小了0.002 9、0.002 6、0.002 3 mm，约为1.67%、1.54%、1.35%；Frictional接触方式中，27SiMn与结构钢相比，最大位移随地面强度变化分别减少了0.021、0.021 9、0.021 2 mm，约为10.79%、11.44%、11.85%。液压缸采用27SiMn可显著减少液压顶升装置的最大位移，且随地面强度增加而显著减少。这是由于地面强度增加，减少了底板的挠度与液压顶升装置的倾斜位移[27]。液压缸材料为结构钢时最大应力值显著大于其他材料，最大应力差值约为30 MPa，且随地面强度增加而减少。采用45号钢与27SiMn，最大应力差值约为5 MPa，差值随地面强度增加而减少。相比而言，液压缸材料为结构钢的液压顶升装置受地面强度影响较大。

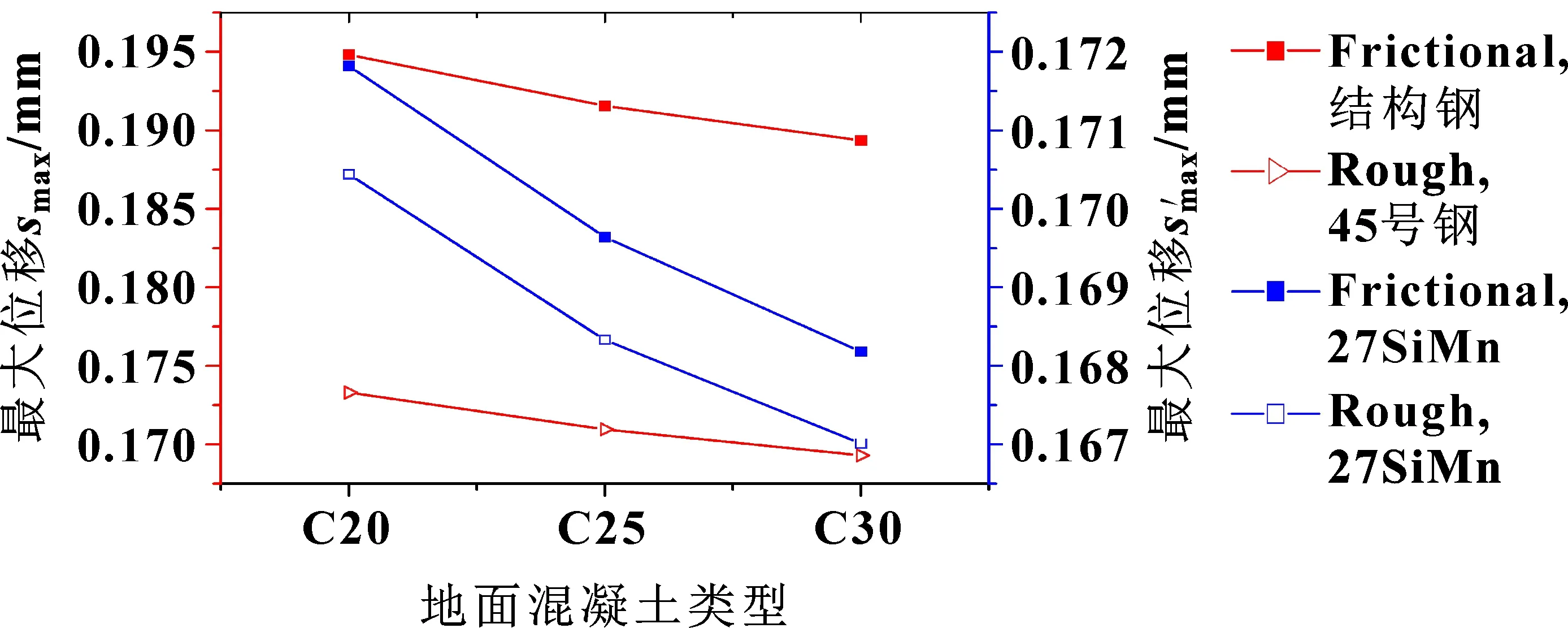
图11 不同接触方式与液压缸材料时液压装置最大位移随地面强度的变化曲线

图12 不同地面强度及液压缸材料时液压装置最大应力的变化曲线

3.5 液压装置最大应力-应变随摩擦因数的变化规律分析

液压顶升装置底板与地面的Frictional接触摩擦因数变化时，液压顶升装置的最大位移与应力变化规律如图13所示。

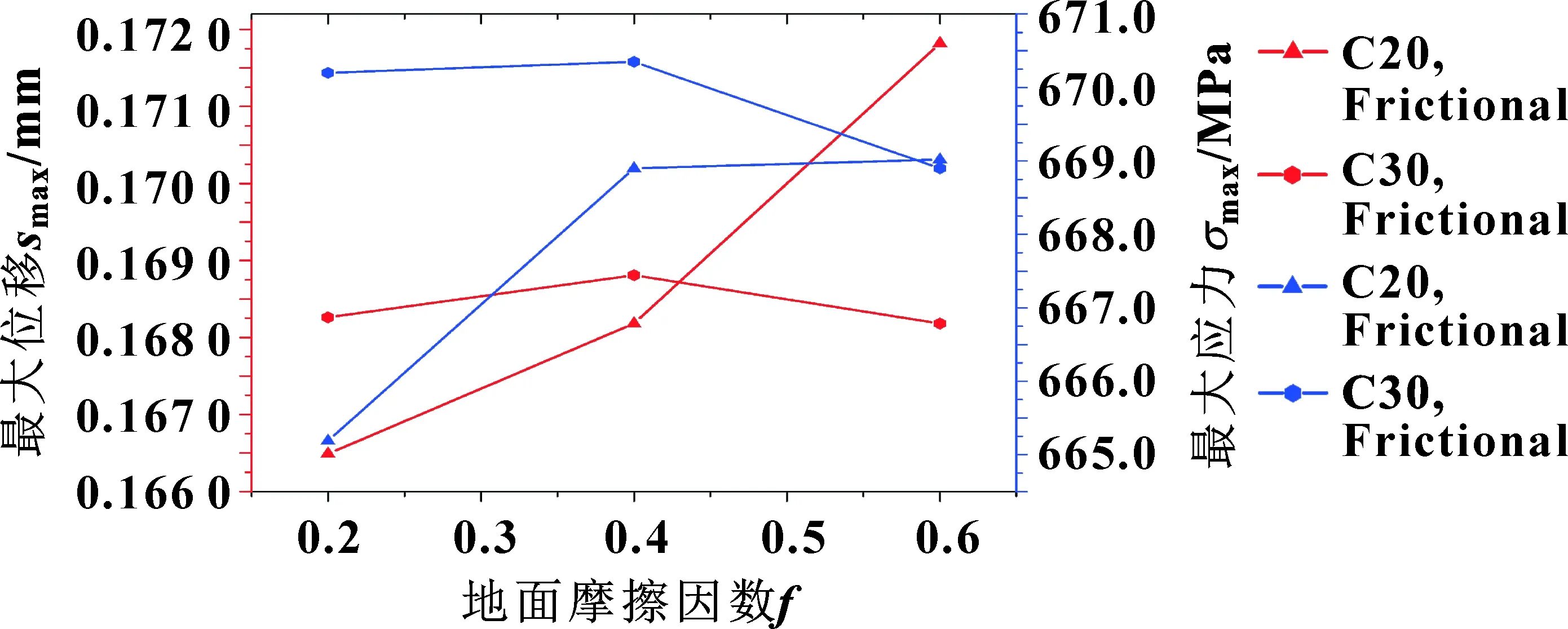
图13 不同地面强度与接触方式时最大位移与应力随摩擦因数的变化曲线

C20地面时，最大位移值随摩擦因数增加且幅值分别为0.001 7、0.003 6 mm；最大应力值随摩擦因数增加且增加幅值变小，分别为665.9、668.9、669.02 MPa。随摩擦因数增加，由地面与底板引起的倾斜变形增加，位移减少。C30地面时，最大位移随摩擦因数先增加后减少，分别为0.168 18、0.168 81、0.168 28 mm，最大应力分别为668.9、670.35、670.2 MPa。摩擦因数对最大位移与应力的影响随地面强度变化而不一致，具有非线性，在设计超高压密封结构时需要综合分析，这与文献[2,32]相似。较低摩擦因数时，C20与C30最大位移间差值较大，且差值随摩擦因数增加先减少为0后又增加；最大应力间差值先快速缩小后又缓慢减少。随摩擦因数的增加，地面强度对最大应力与位移的影响先减小后增加。其中位移临界值在摩擦因数约为0.43时，最大应力临界值在摩擦因数为0.59左右。应力摩擦因数临界值大于位移摩擦因数临界值，这是由于随摩擦因数增加，地面强度对倾斜变形影响减小。这说明，可以通过改变地面摩擦因数来改善液压顶升装置的受力状态，其效果等同与提升地面强度，使位移与应力达到预期状态。

3.6 液压缸的位移、应力影响分析

通常，为了减少地面不平整对液压顶升装置使用性能的影响，在底板与地面间增加一层结构钢，不同工况下位移、应力分别如图14与图15所示。液压缸材料为27SiMn时，结构钢作为地面能显著减少最大位移，且摩擦因数为0.6时[22]，Frictional接触方式下减幅值分别达到14%、12.8%、12%；Rough接触方式下减幅值分别为14.3%、13.2%、12.5%。地面材料为结构钢时，液压缸采用45号钢，其最大位移依然高于27SiMn，最大应力变化与此相似。地面材料由混凝土变为45号钢时，降低的应力幅值未超过1 MPa，这说明结构钢是通过减少由地面变形导致的液压顶升部件的位移，从而有效减少极限位移。

图14 不同接触方式、液压缸材料与地面强度时，最大位移变化的曲线

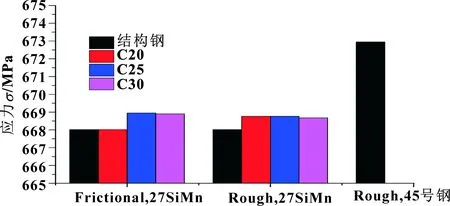
图15 不同接触方式、液压缸材料与地面强度时最大应力变化柱状图

3.7 液压缸不同位置的应力与位移分析

底板与地面接触方式为Frictional，摩擦因数为0.2，地面混凝土类型分别为C30、C20时，靠近液压缸外表面的一孔侧直线位置的位移均小于二孔侧。在较低地面强度下，其差值稍大且其差值随液压缸位置由低端向顶端呈现先增加后减少、再增加又减少的趋势；位移值均保持着先快速增加后缓慢增加，略微减少后又增加的趋势，如图16所示。C20与C30地面时，液压缸同长度不同位置侧，最大差值分别约为0.017 5、0.018 5 mm。液压缸径向位移为非线性，这与文献[14]结论一致。C30地面强度时，液压缸内表面位移规律更加多变，如图17所示。C20地面强度时，极限位移更加接近顶端。C20、C30地面强度时，外表面一孔侧与二孔侧极限位移的位置距离液压缸末端分别约为125、100 mm与150、125 mm；内表面中，C20与C30极限位移的位置距离液压缸末端分别为144、90 mm。一孔侧的极限位移比二孔侧的位置更加靠近顶端。

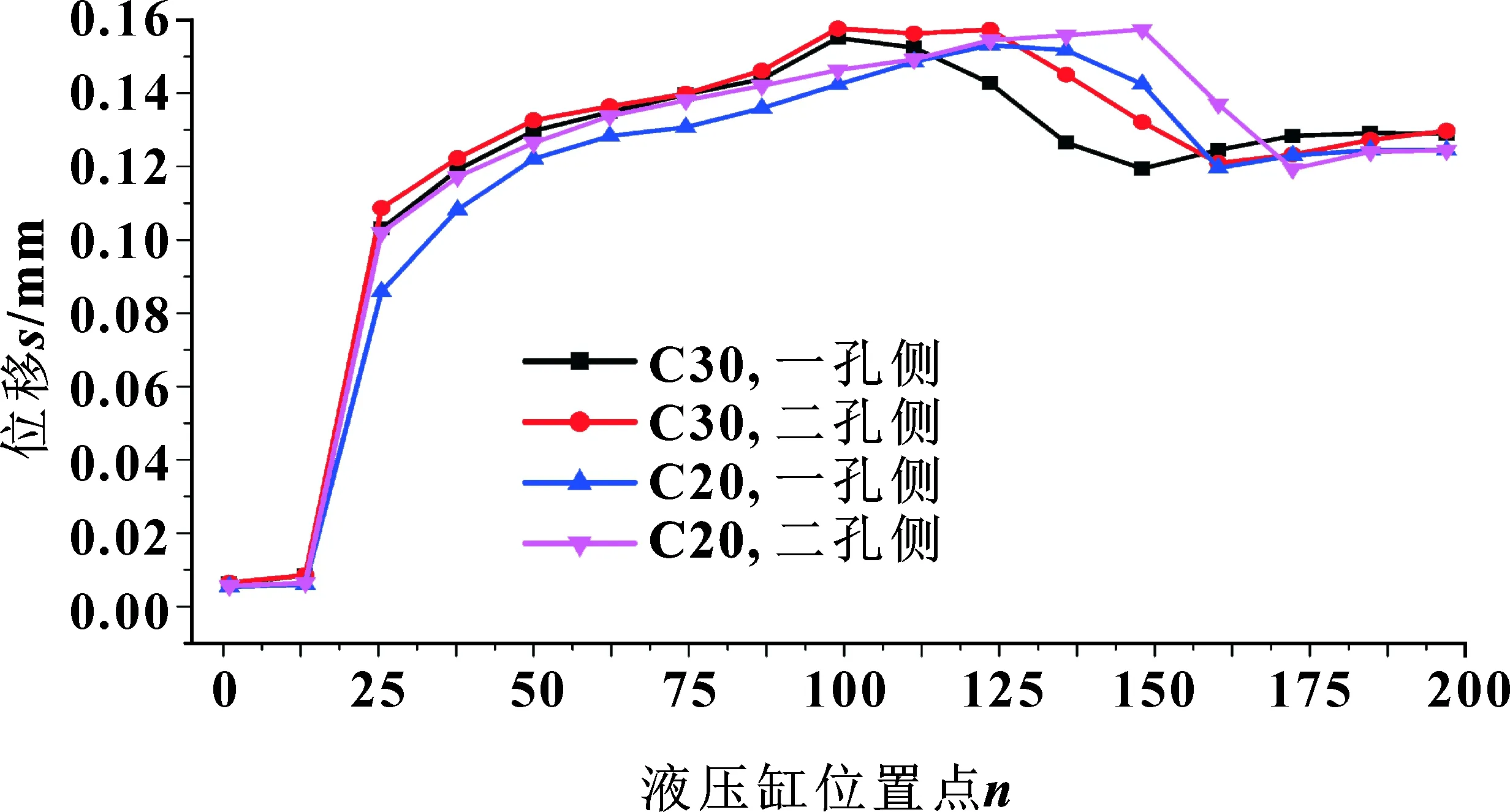
图16 不同地面强度时位移随液压缸长度变化曲线

图17 不同地面强度时液压缸内表面位移随液压缸长度变化曲线

图18展示了应力变化呈现快速增加、缓慢增加、略微减少、略微增加后快速下降的趋势。图19中，内表面应力变化基本保持着一致的趋势，而极限应力值随地面强度增加。C30与C20地面时，液压缸底端应力值随地面强度增加，一孔侧与二孔侧交替出现极大值。液压缸极限应力值处于中间偏上或偏下位移，即离液压缸底面26 mm或91 mm处。底端或顶端的相近位置，内侧应力小于外侧；中间位置，内侧应力值快速超越外侧，外侧应力坡度小于内侧。在一定条件下，可以通过提高液压缸内表面硬度减少液压缸的极限位移。

图19 不同地面强度时液压缸内表面应力随液压缸长度变化曲线

4 结论

分析了超高压液压装置的液压系统等效刚度、频率、应力、应变等的变化规律。液压顶升压力试验的应力值与有限元计算结果较为接近，这证实了有限元模型及边界条件的有效性，主要结论如下：

(1)液压系统等效刚度随液压缸内径而增加。随振幅增加，液压系统的弹簧刚度显著下降；液压缸内径较大时，相对较小的振幅对液压系统的刚度影响较小，且影响系数随内径而增大。液压缸内径不变，改变管道的长度与内径可以显著减少振幅对液压系统刚度的影响，但对液压系统极限刚度影响不大。应首先通过改变内径来提升液压系统刚度。与C20地面相比，C30地面时，液压系统1、2、3阶固有频率分别减少了3.5%、3.5%与20%，1、2阶位移均增加了26%，3阶位移减少了33%。随地面强度增加，1、2阶最大位移快速增加，3、4阶位移快速减少，固有频率降低，且随阶数增加固有频率降低幅值增大。

(2)液压顶升装置极限位移随地面强度增加而显著减少。Bonded最小，Frictionless最大，且随地面强度增加而显著减少。Bonded接触方式，装置的极限位移下降幅值随地面强度增大而快速增加，显著减少了极限应力值。27SiMn材料液压缸可显著减少液压顶升装置的极限位移与应力。液压缸材料为结构钢，液压顶升装置受地面强度影响较大。

(3)摩擦因数对最大位移与应力的影响随地面强度变化而不一致，具有非线性。C20地面时，最大位移值随摩擦因数增加幅值增加。C30地面时，最大位移随摩擦因数增大先增加后减少，位移与最大应力摩擦因数临界值分别为0.43、0.59。可通过优化地面摩擦因数来改善液压装置的应力状态。

(4)液压缸材料为27SiMn时，结构钢地面能显著减少最大位移，且摩擦因数为0.6时，Frictional接触方式下减幅分别达到14%、12.8%、12%；Rough接触方式下减幅分别为14.3%、13.2%、12.5%。液压缸采用45号钢，其最大位移依然高于27SiMn。在底板与地面间增加结构钢能有效减少极限位移。

(5)液压缸外表面接近一孔侧直线位置的位移均小于二孔侧，均呈现先快速增加后缓慢增加、略微减少后又增加的趋势。C20与C30地面，液压缸同长度不同位置侧，最大差值分别约为0.017 5、0.018 5 mm。液压缸径向位移为非线性。C30地面强度时，液压缸内表面位移规律更加多变。C20地面强度时，极限位移更加接近顶端。