基于罚函数遗传算法的水土保持土方调配优化
2023-10-11霍正刚王子旸查晓庭张森森陆孟瑶
霍正刚, 王子旸, 查晓庭, 张森森, 陆孟瑶
(扬州大学建筑科学与工程学院, 江苏 扬州 225127)
随着中国城市化进程的快速发展, 如何平衡规模不断扩大的城市建设和城市的水土保持已成为城市规划和建设过程中亟需解决的问题之一, 而环境友好、资源友好型的工程项目有利于我国经济的持续发展.水土保持项目涉及场平工程、土石坝工程、路堤工程和地下工程等, 这些工程均须考虑土方的调配问题, 包括地上与地下之间的调配、不同场地间的调配等.目前, 土方调配问题通常归结为管理运筹学中的运输问题,并将土方调配优化模型问题转化为线性关系, 以线性规划为基础建立理论框架, 运用数学方法得到最优解.景明等[1]采用LINGO工具对大型土方调运问题进行线性规划求解, 所得结果较为准确; Artun等[2]通过垂直优化的单纯形法求解线形规划模型, 较大幅度地降低了优化后的成本; Karimi等[3]考虑到土方挖填区体积和单价的模糊性, 提出一种土方调配模糊线性规划模型; Liu等[4]建立具有模糊参数和约束的全系数模糊线性规划土方分配模型, 有效克服了传统土方分配方法的不足; Wan等[5]利用线性规划模型, 采用表格运算法对土方调配进行优化, 最小元素法确定初始运输方案,并通过闭路法优化方案, 最终得到最小土方运费的方案.这些研究成果显示, 线性规划因采用严格的数学方法建模, 故不管是表格法还是表上作业法其计算量均较大, 且计算时易陷入局部最优解.Katebi等[6]采用一种稳健优化方法对传统道路施工中土方调配的规划模型进行修正, 使该模型具有较好的鲁棒性; Villar等[7]利用ICOM(intelligent method of optimized mass compensation)方法对经典的土方挖掘和填充过程进行优化, 该方法能有效降低土方挖掘与填充的成本; Akgul等[8]运用无人机和全球卫星导航系统, 提高了土方计算中网格的分辨率, 使土方调配精度大幅提高; Shehadeh等[9]基于进化多目标方法提出一种新型优化系统, 使时间和成本分别下降了14.35%和9.50%.这些方法的优点是计算方便, 但在模型的解释性上不如线性规划, 计算结果的准确性也存在不足.本文以某水土保持项目为研究对象, 拟采用线性规划法并结合罚函数基因遗传算法对该水土保持土方调配进行快速优化, 为解决类似土运问题提供参考.
1 土方调配模型
1.1 基本假设
本文建立的土石方调配模型基于以下几个假设:
1) 土方之间的运输路线按照最短直线距离进行.由于土方调配工程中施工现场地形的不规则性和不一致性, 通常采用面积中心或几何中心计算两个区域之间的距离.
2) 每个工段既可以是挖区也可以是填区, 各挖填区的土方量已知, 且满足挖填总体平衡, 忽略挖填土方的临时变更量.
3) 因实际工况中, 中转场地只是起到临时存储作用, 并不影响最终土方调运区域之间的调配关系, 故不考虑中转场地的影响.
1.2 变量参数符号及含义
土方调配的费用组成主要由单位体积综合单价、运距及土方调配量构成,表1 给出了本文模型中各参数的符号及含义.

表1 变量符号及含义
1.3 综合单价
1.4 目标函数及求解
1.4.1 目标函数及其约束条件
在同一工段内进行挖掘和填筑时, 因不涉及运输调配量, 故有Xii=0; 而各工段间的距离在设计阶段已经确定, 故Sij为常量.因此, 总运费的线性规划函数
(1)
则土方调配模型的目标函数
(2)
其约束条件为
(3)
1.4.2 带罚函数的目标函数
为解决遗传算法求解土方调运过程中的约束优化问题时可能存在不可行解产生偏离可行域的解和遗传因子作用于可行解后产生不可行解的问题[12], 本文采用罚函数使其转化为无约束问题后再求解.此时, 无约束带罚函数的目标函数
g(Xij)=f(Xij)/Cij+kp(Xij),
(4)
其中k为惩罚因子.当Xij取值符合约束等式条件时, 罚函数p(Xij)不起作用或作用很小; 当Xij取值不符合约束等式条件时,p(Xij)起作用, 此时g(Xij)增大, 适应度变小, 不易被复制而遗传给下一代.因此, 式(3)中的等式约束利用罚函数变成无约束形式, 令约束函数
(5)
(6)
1.4.3 适应度函数
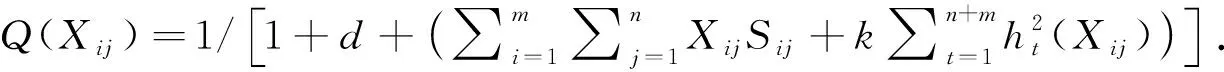
1.4.4 遗传算法求解目标函数
遗传算法是一种模拟自然界优胜劣汰、适者生存的算法[14].其本质是一种排序的算法或是一种选优的算法, 图1给出了这种算法的步骤.但是传统的遗传算法运算量较大,收敛速度较慢, 且当调配数目达到一定程度时易陷入局部最优而不能得到最优解.为解决这些问题, 本文在目标函数上引入罚函数[15], 此时线性规划问题的求解步骤为:
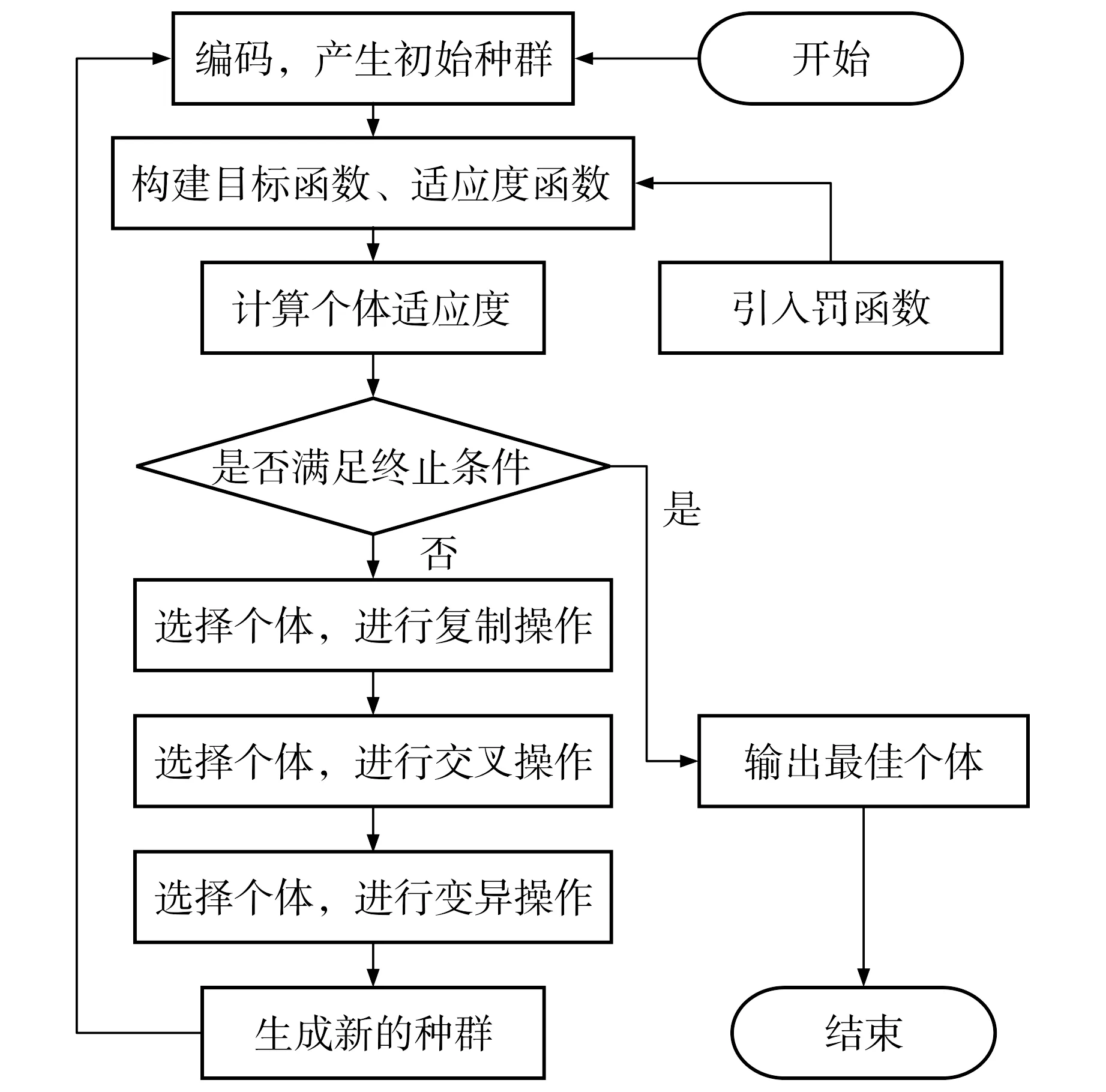
图1 遗传算法流程图Fig.1 The flow chart of genetic algorithm
1) 确定所需种群数量的大小.本文实例中选取初始种群大小为30, 并以各区域间调运土方量Xij作为基因编码个体[16], 用二进制编码将个体基因编码成一个二进制符号串, 其中每一个符号串代表一条染色体.为避免初始种群远离全局最优解编码空间, 根据土方量变动区间随机生成初始种群.
2) 定义一组优化函数.以总运费的线性规划函数式(1)为优化函数, 式(2)为目标函数, 加入罚函数及其他限制参数得到适应度函数.
3) 计算各个体的适应度.以0.60的交叉率对个体进行基因交叉操作, 以0.01的变异率对子代个体进行变异操作.为提高子代中适应度高的个体的比例, 采用轮盘赌法[17]选择个体.
4) 对新产生的子代个体进行适应度计算, 并进行种群的更新.
5) 满足终止条件时算法终止, 并对原始编码信息根据编码的方向进行二进制解码, 输出最终结果, 即区域间调运土方量Xij.
2 仿真实验
2.1 项目简介
扬州市某居住项目土方施工区分为建筑物区、道路广场区、绿化区.其中, 建筑物区包含基础开挖工段W1/T1、场地平整工段W2/T2、场地清淤工段W3/T3; 道路广场区分为管线施工段W4/T4、场地平整工段W5/T5、场地回填工段W6/T6; 绿化区分为绿化覆土工段W7/T7、绿地开挖工段W8/T8、绿地回填工段W9/T9.根据设计方提供的数据, 此项目的开挖及回填的土方量如表2所示.表3给出了不同工段间的运输距离Sij.

表2 各施工段开挖填筑土方量
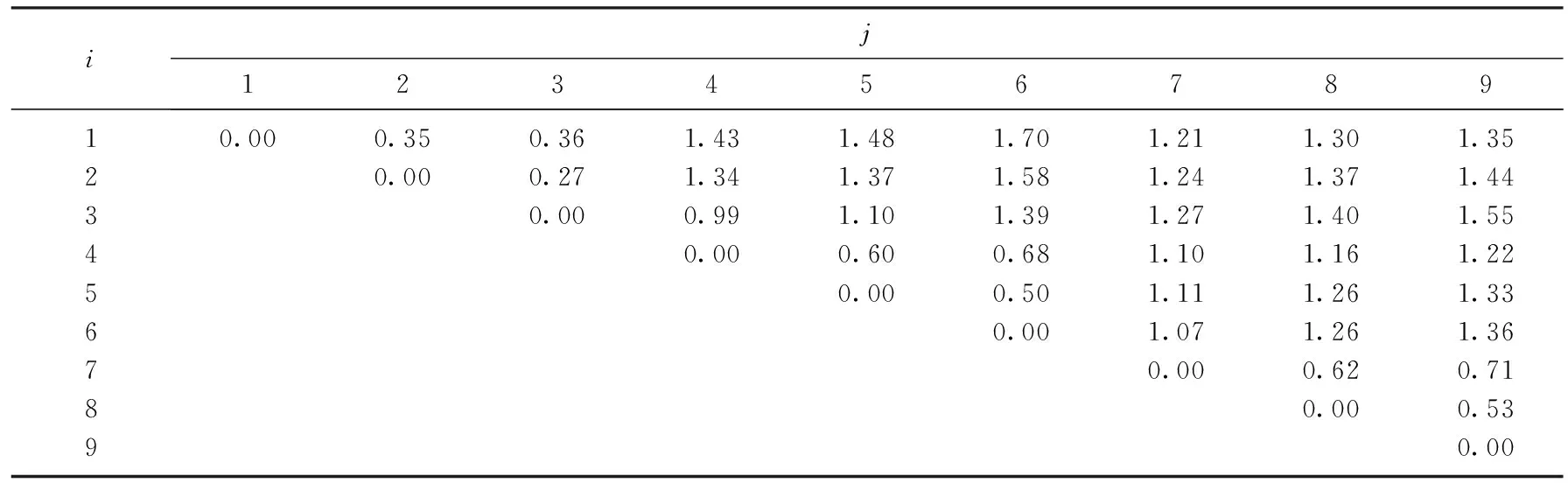
表3 不同工段间的运输距离Sij
2.2 模型简化与约束矩阵
2.2.1 变量及罚函数个数简化
如果i区域挖方量Wi为0.00 m3, 则所有从i区域调运出的Xij为0.00 m3.同理, 若j区域填方量Ti为0.00 m3, 则所有调往j区域的Xij为0.00 m3, 且挖填自给区域的Xii=0.00 m3, 故该项目的未知变量Xij可从81个简化至12个,约束等式从18个简化为7个.此时,简化后的罚函数为p(Xij)=(X15+X16+X17+X18-7.10)2+(X35+X36+X37+X38-1.90)2+(X95+X96+X97+X98-1.68)2+(X15+X35+X95-0.45)2+(X16+X36+X96-2.96)2+(X17+X37+X97-1.25)2+(X18+X38+X98-6.03)2.适应度函数则化简成由12个变量及7个约束等式求平方和的复合函数, 使函数的求解更方便.
2.2.2 参数设置
惩罚系数k=30.00; 带罚函数的目标函数
Q(Xij)=1.48X15+1.70X16+1.21X17+1.30X18+1.10X35+1.39X36+
1.27X37+1.40X38+1.33X95+1.36X96+0.71X97+0.53X98+30.00p(Xij);
约束条件为W=(7.10,0.00,1.91,0.52,0.00,0.00,0.00,0.00,1.68),T=(0.00,0.00,0.00,0.52,0.45,2.96,1.25,6.03,0.00); 隐含条件为Xij≥0.
2.3 结果与分析
2.3.1 仿真结果
运用MATLAB中遗传算法工具箱, 输入带罚函数的目标函数, 下限设置为Zeros(12,1), 种群规模设为200代.图2为优化过程的运行曲线.从图2可以看出, 遗传算法在迭代30次后曲线趋于平稳, 染色体随迭代次数的增加差异较小, 表明已经找到最优解.在最优条件下该项目的土方调用结果为:X15=4.30×103m3,X16=1.77×104m3,X17=6.70×103m3,X18=4.23×104m3,X36=8.10×103m3,X37=3.70×103m3,X38=6.90×103m3,X96=3.70×103m3,X97=2.00×103m3,X98=1.11×104m3.
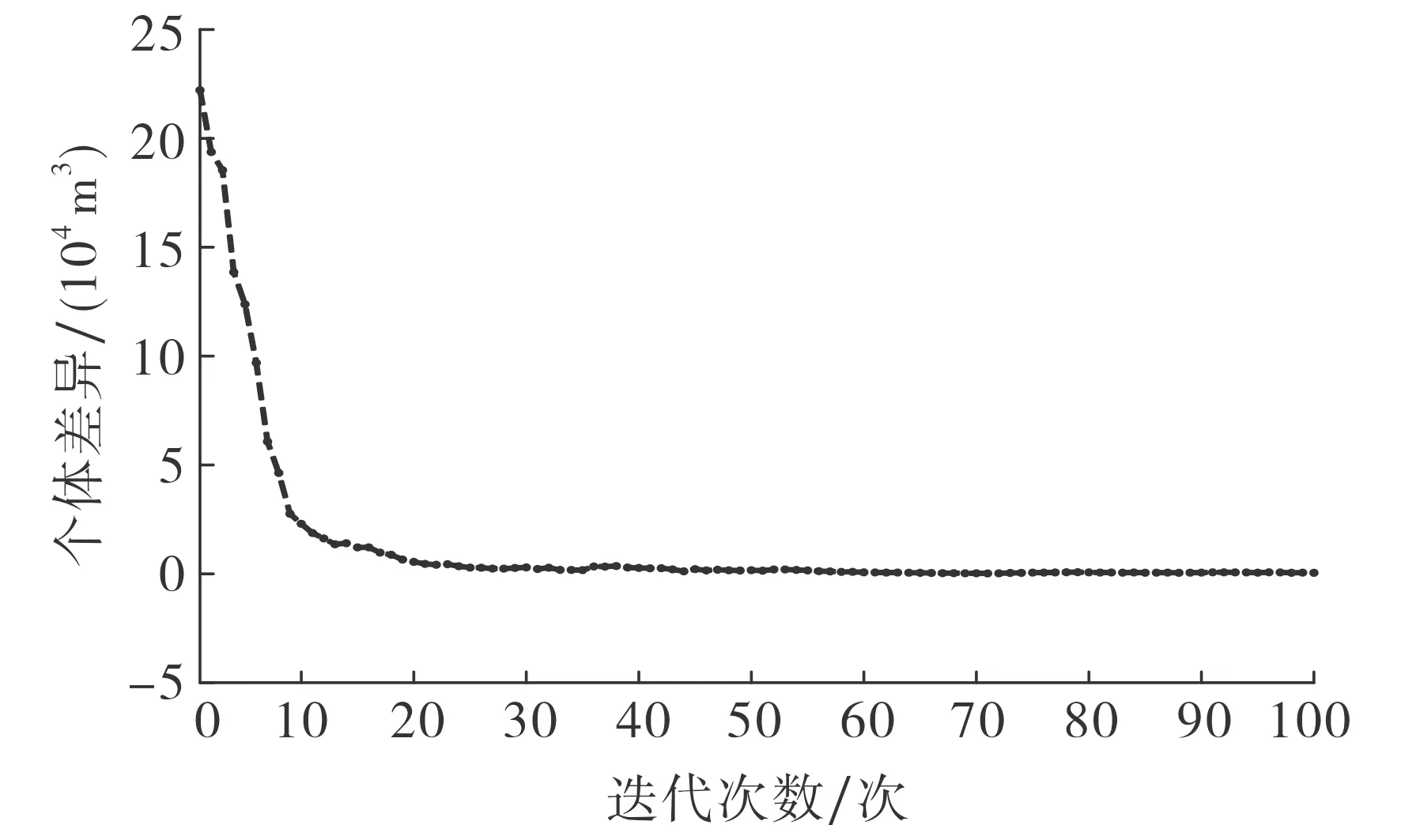
图2 遗传算法运行曲线Fig.2 Genetic algorithm running curve
2.3.2 不同算法结果比较
假设运输的综合单价为1.00元·m-3·km-1, 不同算法中各区域运输距离一致.
1) 表上作业法. 图3为该项目实际工程的传统表上作业法求解调运结果.根据式(2)将传统算法下土方调配量与距离矩阵点乘求和, 表上作业的运输规划按照图3的箭头方向调运, 则运费总和为13.94万元.此法不能通过有关条件简化工作, 计算工作量大而繁杂.
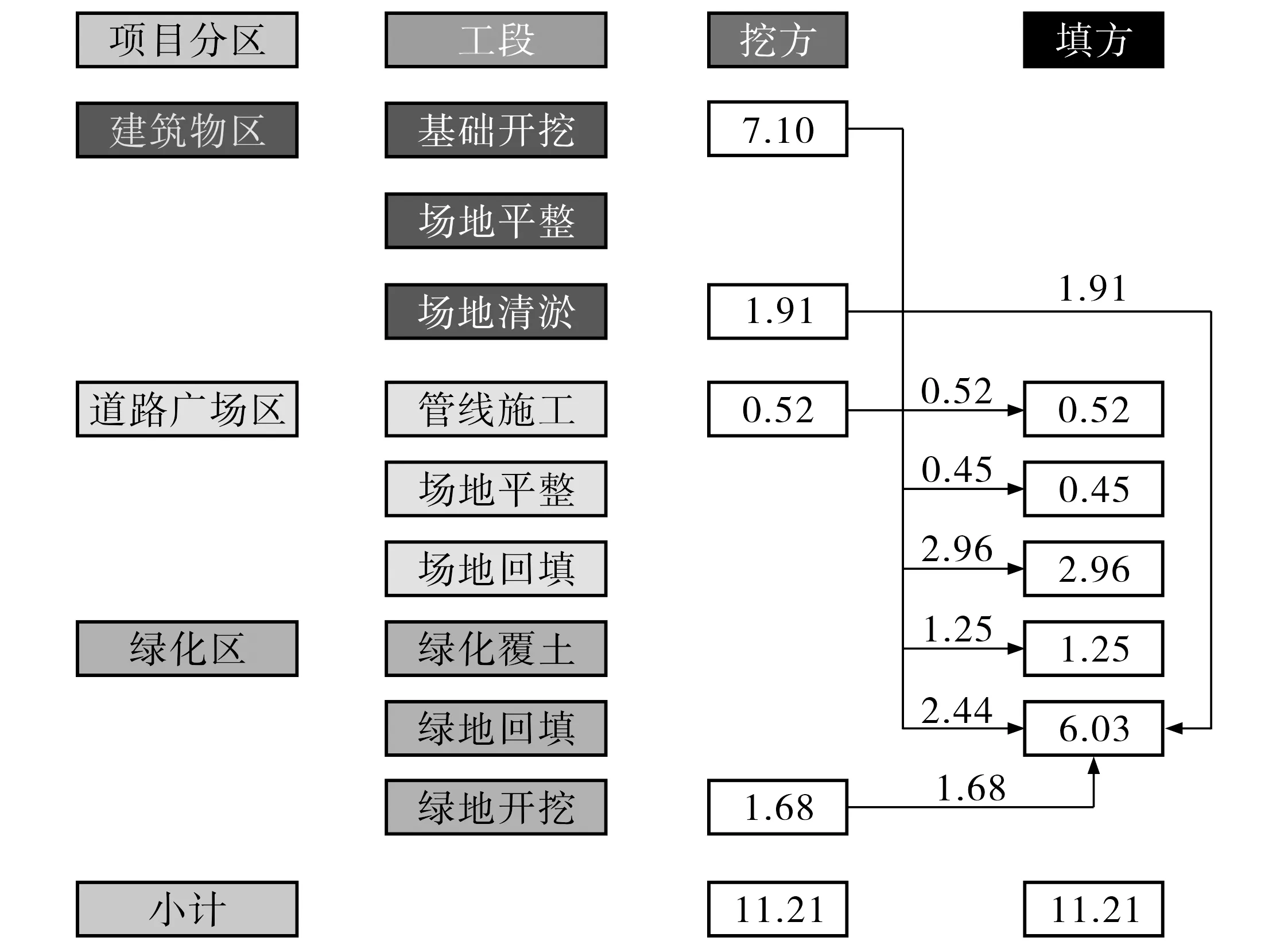
图3 表上作业法土方平衡图(104 m3)Fig.3 Earth balance diagram for table operation method
2) MATLAB自带线性规划工具箱算法. 函数写成调用格式, 等式约束矩阵选取W、T, 下限为L=Zeros(12,0), 线性规划优化函数为 [X,faval]=linprog(g(Xij),0,0,W,T,L), 运行自带线性工具箱, 得X=(0.45,2.96,1.25,2.44,0.00,0.00,0.00,1.91,0.00,0.00,0.00,1.68).取对应的距离矩阵S=(1.48,1.70,1.21,1.30,1.10,1.39,1.27,1.40,1.33,1.36,0.71,0.53)进行点乘求和, 得到总费用为13.94万元, 结果与表上作业法一致.该算法由计算机完成, 故计算速度更快, 人为误差更少.
3) 罚函数遗传算法.根据公式(2)将带罚函数遗传算法结果的变量值与运输距离矩阵点乘求和, 得运费总和为13.75万元.计算结果表明, 罚函数遗传算法结果优于传统表上作业法和线性规划工具箱结果,且收敛速度更快.
上述仿真结果表明, 与表上作业法比较,罚函数遗传算法避免了手工计算, 可以通过具体问题条件简化方程, 能快速且准确地得到最优解; 与MATLAB自带线性规划工具箱比较, 罚函数遗传算法所得调运费用结果优于线性规划工具箱.因此, 在复杂问题上, 采用罚函数遗传算法优化线性规划问题时求解速度更快, 规划质量的结果更精确.
3 结论
对于复杂问题, 遗传算法在求解速度和质量上均远超常规方法.仿真实验过程表明, 遗传算法只是一种近似算法,在运用的过程中需要巧妙的构思来简化变量数量, 利用罚函数避免不可行解或可行域外的解.总之, 罚函数遗传算法为计算约束优化问题提供了一条可行的途径, 通过合理规划和合理搭配, 实现了一定的经济价值.
