基于环形拓扑结构和动态邻域的多模态多目标粒子群优化算法

章恩泽, 赵哲萱, 韦静月, 葛 蕤, 蒋 超

(扬州大学信息工程学院, 江苏 扬州 225127)

在工程实际中广泛存在着一类具有多模态特性的多目标优化问题, 其决策空间存在2个或以上Pareto最优解集对应于目标空间同一Pareto前沿, 该类问题被称为多模态多目标优化问题(multimodal multi-objective optimization problems, MMOPs), 如路径规划问题[1]、建筑选址问题[2]或结构优化设计[3]等．由于大多数已有的多目标优化算法鲜少关注解在决策空间中的多样性, 所以在求解MMOPs时通常难以得到分布性良好的Pareto最优解集．近年来, 一些改进的MMOPs求解算法被相继提出．Yue等[1]提出基于环形拓扑和特殊拥挤距离的多目标粒子群优化算法(multi-objective particle swarm optimization algorithm with ring topology and special crowding distance, MO_Ring_PSO_SCD), 通过环形拓扑结构限制种群内的信息传递速度, 使得种群在搜索过程中逐渐形成稳定的小生境, 从而找到更多的Pareto最优解; Hu等[4]在多模态多目标鸽群算法(multimodal multi-objective pigeon-inspired optimization, MMOPIO)中采用映射方法将原始决策空间转化到映射空间, 并根据粒子在映射空间的分布确定其邻域关系, 使得种群在映射空间邻域内进化; Zhang等[5]通过决策空间聚类方法将整个种群分为多个子种群, 子种群内的粒子根据全局最优位置更新位置和速度, 不同种群之间采用环形拓扑结构进行信息传递; Qu等[6]采用自组织方法将种群划分为多个子种群进行并行搜索, 提出了自组织多目标粒子群优化算法(self-organized speciation based multi-objective particle swarm optimizer, SS-MOPSO); Zou等[7]采用改进的差分进化策略扩大搜索范围, 并利用近邻移动策略使粒子向最优解逼近且在局部范围内进行优化．上述MMOPs求解算法均难以获得完整的Pareto最优解集, 且种群多样性仍有待提高．为更有效地求解MMOPs, 本文基于无重叠环形拓扑结构构造粒子邻域, 采用邻域最优位置替代种群的全局最优位置进行粒子更新, 并引入周期重组(periodic recombination, PR)和一种全局最优位置更新(global best position updating, GBPU)策略, 拟提出一种新的多模态多目标粒子群优化算法(ring topology and dynamic neighborhood based multi-objective particle swarm optimizer using periodic recombination and global best position updating, RDNMOPSO-PR-GBPU)．

1 RDNMOPSO-PR-GBPU算法

1.1 采用邻域最优位置的粒子群算法

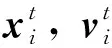
(1)

(2)

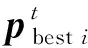
PSO算法的收敛性虽较强, 但容易陷入局部最优, 故将式(1)中的全局最优位置替换为邻域最优位置nbest, 进行PSO更新[8]:

(3)

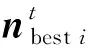
1.2 基于空间距离的无重叠环形拓扑结构

粒子群的拓扑结构决定了种群中粒子间的信息交换方式, 从而直接影响算法的收敛速度．在环形拓扑结构中, 粒子仅与其相邻的两个粒子共享信息, 并根据各自邻域最优位置进行更新,因而能够发现更多最优解[8]．常见的环形拓扑结构一般根据粒子的索引构建邻域, 如图1所示, 其中1号、2号粒子编号虽相邻, 但在决策空间中距离却较远, 因此该类邻域关系并不能反映粒子在决策空间中的真实分布, 导致搜索效率下降．

图1 基于索引的环形拓扑结构Fig.1 An index-based ring topology structure

为更好地体现粒子在决策空间中的分布, 本文充分考虑粒子在决策空间和目标空间的多样性, 提出一种基于空间距离的无重叠环形拓扑结构, 如图2所示．对种群中所有粒子按照非支配关系和特殊拥挤距离[1]进行优劣排序, 将排名前Ndms个粒子归类为小型子种群, 其余Ndisad个粒子归入劣势子种群．由于各子种群相互独立且进行并行搜索, 所以种群的多样性可进一步得以提升．以图2中种群规模为10的粒子群为例, 根据基于特殊拥挤距离的非支配排序方法[1]对粒子进行排序, 将编号为1、4、3的粒子置于第一个小型子种群Dss1, 将编号为2、6、5的粒子置于第二个小型子种群Dss2,Dss1和Dss2分别追随拓扑结构中粒子的邻域最优位置进行并行搜索．剩余编号为7、8、9、10的粒子在决策空间中分布较松散且距离邻域最优解较远, 为了提升搜索效率, 将此类粒子并入劣势子种群Ndisad, 利用全局最优位置引导其向更好的区域进行搜索．

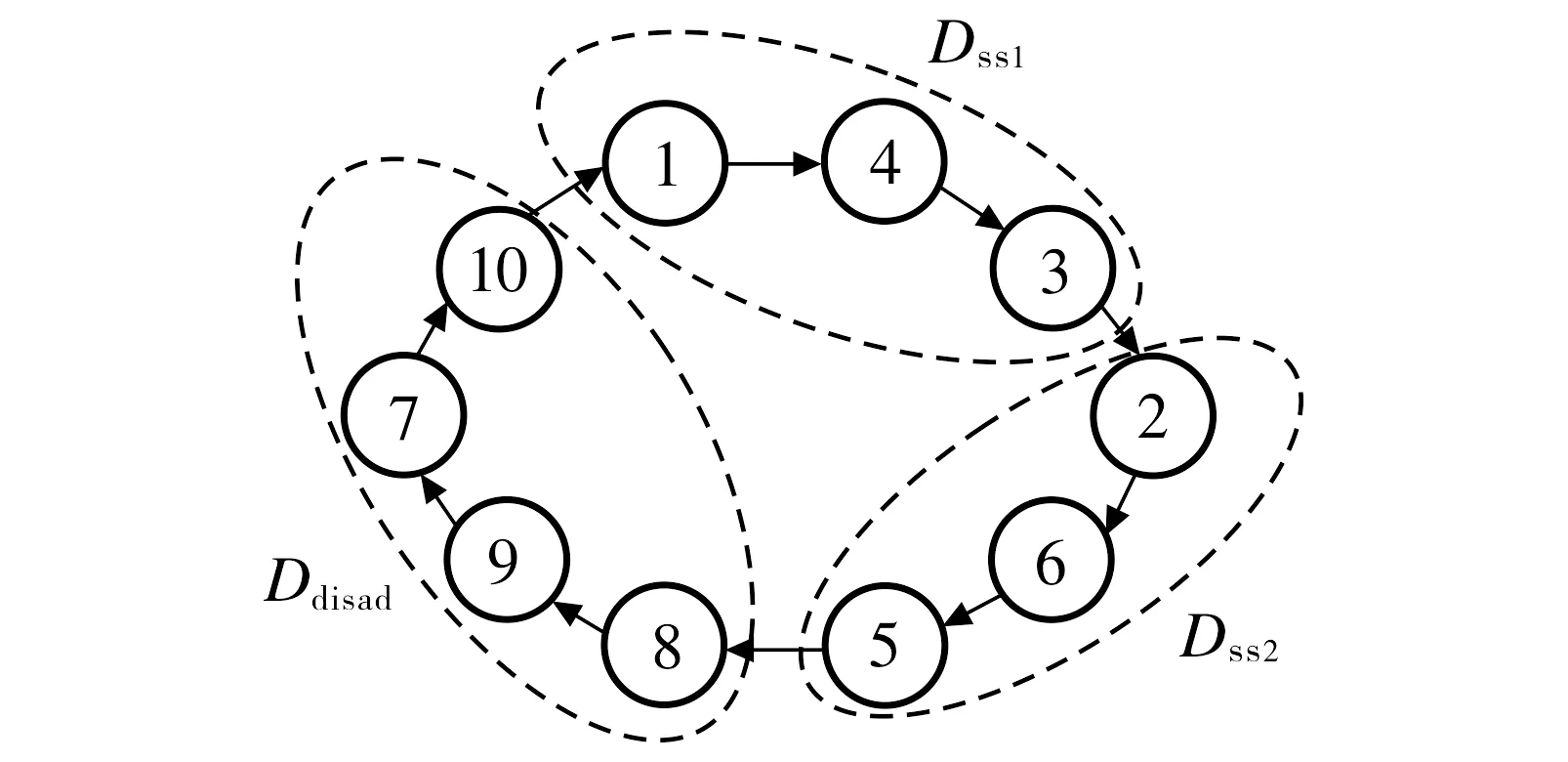
图2 基于空间距离的无重叠环形拓扑结构Fig.2 A non-overlapping ring topology based on the distance structure

1.3 全局最优位置更新策略

对于PSO算法,全局最优位置的选择直接影响整个种群的搜索方向和最终解集的质量,因而在利用PSO算法求解多目标优化问题时,为每个粒子选择合适的全局最优位置成为算法设计的关键[9]．针对多模态多目标优化问题,本文通过在已有邻域最优位置的周围进行局部搜索,以获得潜在的分布性更优的全局最优位置,从而在引导种群逼近Pareto最优解集的同时维护其多样性．本文设计的全局最优位置更新策略的步骤如下:

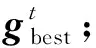
2) 在所有小型子种群的邻域最优位置附近生成一个新的粒子, 并计算其目标函数值;

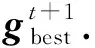
1.4 周期重组

小型子种群采用无重叠环形拓扑结构, 增加了搜寻到最优解的可能性, 但由于粒子间信息流动过于单一, 粒子可能表现出“趋同性”, 即一旦某一粒子陷入局部最优, 则可能导致与之处于同一邻域的其他粒子处于停滞状态．为引导粒子跳出局部最优, 现引入周期重组策略, 以增强算法的探索力度和开拓搜索范围．周期重组策略的具体步骤如下:

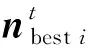
2) 保存Dss i中所有粒子的个体最优档案(personal best archive, PBA)和邻域最优档案(neighborhood best archive, NBA);

3) 对Dss i中粒子重新进行初始化操作, 将随机新生成的粒子加入下一代种群中;

4) 根据式(2)(3)更新Dss i中粒子, 并将更新后的粒子加入到下一代种群中．

2 仿真结果与分析

为验证本文算法的有效性, 现设置3组对比实验进行仿真分析: 比较参数Ndms和Ndisad取值对算法优化结果的影响; 对比引入周期重组和全局最优位置更新策略前后算法性能的有效性; 对比本文算法与5种已有多目标优化算法的性能．所有实验均通过MATLAB 2020b编程实现, 计算机配置为Intel(R) Core(TM) i5-9400F@2.90 GHz, 16 GB RAM．采用8个多模态多目标优化测试函数MMF1～MMF8[1]综合测试算法的性能．

2.1 性能评价指标

选择决策空间反世代距离(the inverted generational distance in the decision space, IGDX)[10]和Pareto解集逼近度(Pareto sets proximity, PSP)[1]作为评价指标, 评价算法的性能．

IGDX可衡量获得的解集与真实Pareto解集的近似程度．对于解集X, 有

其中D(x,y)为解x和解y的欧氏距离,X*为真实Pareto解集中的均匀采样, |X*|为集合X*中解的总个数．IGDX的值越小, 表明解集的收敛性和多样性越好．

2.2 参数取值的影响

设置种群规模为600, 当小型子种群Ndms与劣势子种群Ndisad之比r分别为2,4,6,8,10,12时, 参数Ndms和Ndisad的取值如表1所示．

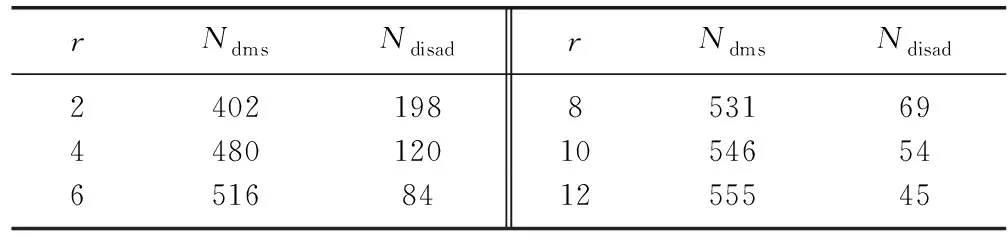
表1 不同r值下Ndms和Ndisad的取值

图3给出了不同r值下算法运行30次所得PSP均值．由图3可见: 当r=8时, 在除MMF5和MMF6外的其余6个测试函数上PSP均值都最大, 表明该取值下小型子种群和劣势子种群的数目使算法在探索和开发之间实现了更好的权衡, 从而获得更好的综合性能．

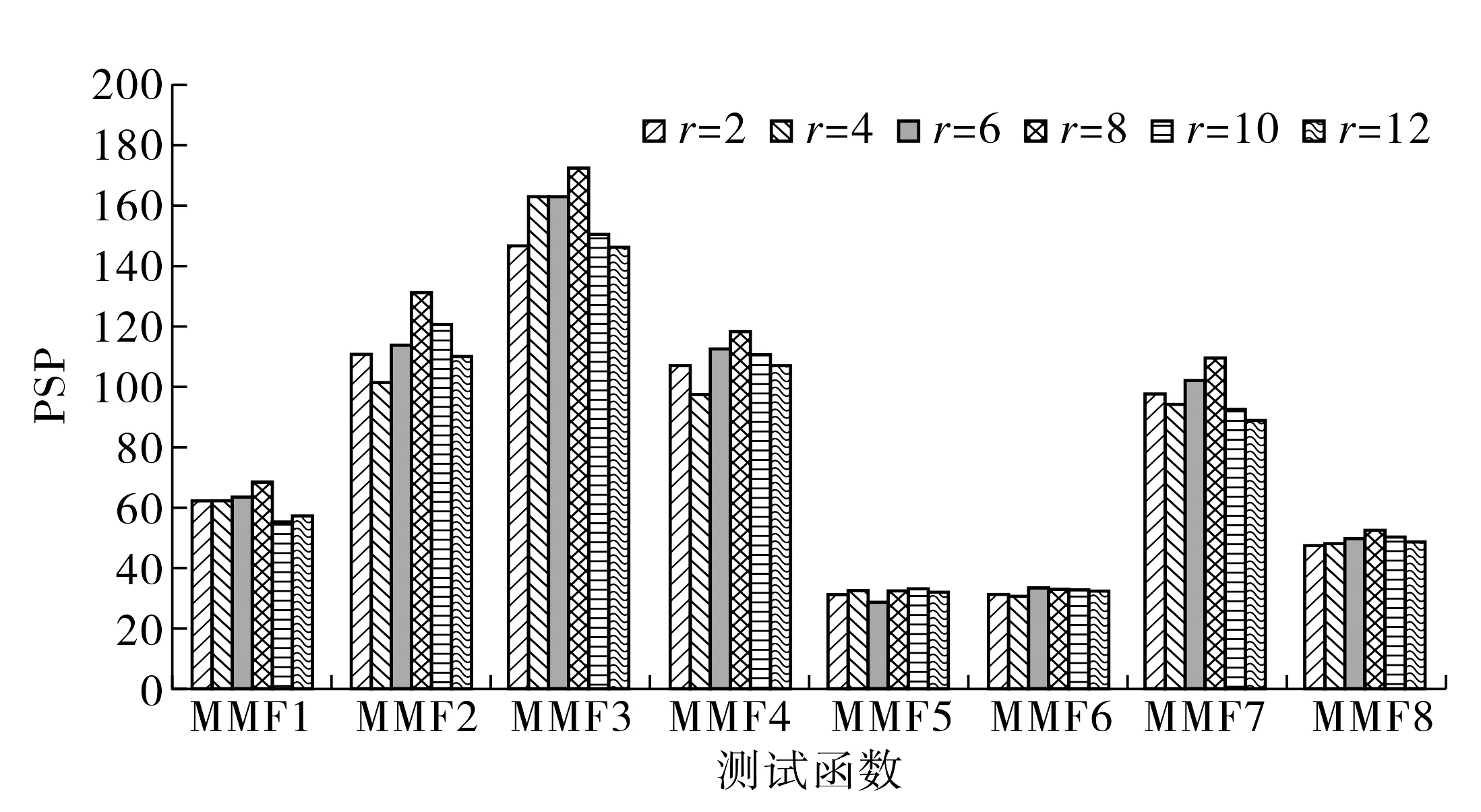
图3 不同参数取值下算法所得PSP均值Fig.3 PSP mean values obtained by the algorithm under different values of parameter

2.3 周期重组和全局最优位置更新策略的有效性

对比引入周期重组和全局最优位置更新策略前后算法的有效性, PSP均值如表2所示．由表2可见: 本文算法在8个测试函数上都获得了最优结果, 且在全局和局部Pareto解集共存的测试函数MMF2和MMF3上优势较明显, 说明周期重组和全局最优位置更新策略有助于算法跳出局部最优．

表2 引入周期重组和全局最优位置更新策略前后算法的PSP 均值

2.4 几种算法的性能对比

为进一步验证本文算法的有效性, 现与基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)[11]、多目标粒子群优化算法(multi-objective particle swarm optimization algorithm, MOPSO)[12]、决策空间小生境多目标遗传优化算法(decision space based niching nondominated sorting genetic algorithm Ⅱ, DN-NSGA Ⅱ)[13]、MO_Ring_PSO_SCD[1]和SS-MOPSO[6]等5种算法在8个测试函数上进行对比．所有算法均设置最大评价次数为60 000, 种群规模为600, 每种算法在各测试函数上独立运行30次, 所得IGDX和PSP均值分别如表3～4所示．由表3～4可见: 1) 本文算法虽在MMF3和MMF7测试函数上的IGDX结果略逊于SS-MOPSO和DN-NSGAⅡ, 但在其他6个测试函数上获得了IGDX的最小值; 2) 本文算法在除MMF5外的7个测试函数上PSP值均最大, 表明所提算法在大多数测试函数上获得了更加逼近真实Pareto解集且分布性更好的最优解集．其可能原因是, 作为传统的多目标优化算法, MOEA/D和MOPSO未针对多模态情形进行特殊处理; 相较于DN-NSGAⅡ和SS-MOPSO, MO_Ring_PSO_SCD和本文算法在信息传递时采用环形拓扑结构, 在环境选择中采用特殊拥挤度距离, 大大提高了解集在决策空间的分布性; 本文算法和MO_Ring_PSO_SCD虽然都采用基于拥挤距离的非支配排序方式, 但本文算法因引入周期重组和一种新的全局最优位置更新策略, 故能帮助算法跳出局部最优, 找到更接近真实Pareto最优解的解集．综上, 本文算法在求解多模态多目标优化问题时更有效．

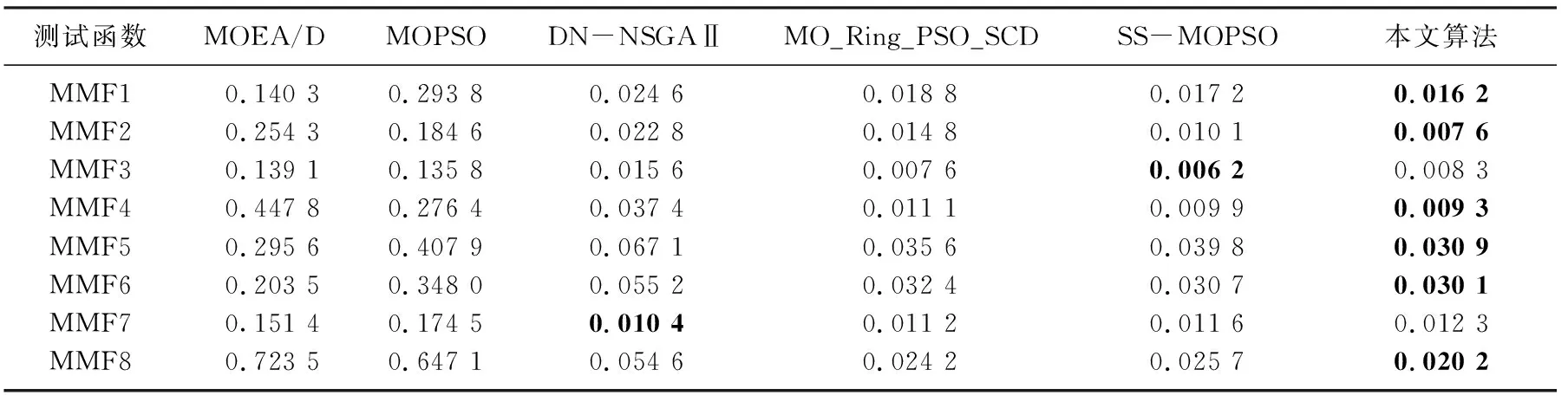
表3 不同算法的IGDX均值

表4 不同算法的PSP均值