一种基于软判决的非删余极化码参数识别算法
2023-10-11黄知涛
王 垚, 王 聪, 王 翔, 黄知涛
(1. 国防科技大学电子科学学院, 湖南 长沙 410073; 2. 陆军工程大学通信士官学校, 重庆 400035; 3. 海军航空大学信息融合研究所, 山东 烟台 264001)
0 引 言
信道编码技术可以有效提升数据传输的可靠性,被广泛应用于各类数字通信系统中。在合作通信中,通信收发双方预先约定所采用的编码参数,接收端利用确定的编码参数对解调后的比特序列进行译码,恢复发送端发射的通信内容。但在认知无线电、非合作通信领域,接收端往往缺乏足够的先验信息进行译码。此时,就需要利用接收到的解调序列,完成对编码参数的识别[1-2]。目前,主要的编码方式包括线性分组码、卷积码、Turbo码、低密度奇偶校验(low density parity check,LDPC)码、极化码等。但从公开发表的文献来看,信道编码参数识别的研究主要集中于线性分组码[3-6]、卷积码[7-9]、Turbo码[10-13]、LDPC码[14-16]。对极化码参数识别的研究,尚处于起步阶段。
极化码是目前唯一一种被证明在二进制离散无记忆信道(binary discrete memoryless channel,B-DMC)下可达到信道容量的信道编码方式[17],并在3GPP RAN1 #87次会议上被确定为5G增强移动宽带场景下控制信道的信道编码方案[18]。同时,极化码在卫星通信和深空探测方面也有不错的应用前景[19]。可以预见,会有越来越多的通信系统采用极化码作为差错控制的手段,对极化码进行参数识别研究具有重要的理论和应用价值。现有针对极化码参数识别的研究,均默认对象为标准非删余极化码。本文同样针对标准非删余极化码展开研究,若无特别说明,文中极化码均指标准非删余极化码。
极化码从编码过程上,可看作是线性分组码的一个子类,但由于其特有的编码理论与方法,现有的线性分组码参数识别方法并不适用于极化码。针对极化码参数识别问题,文献[20]针对二进制删除信道(binary erasure channel,BEC)条件,采用硬判决序列作为处理对象,对删除概率和码长进行遍历,求得每组参数对应的生成矩阵与其零空间,再利用码字矩阵与零空间之间的对偶关系,确定各个参数。文献[21]则利用极化码生成矩阵的结构性质,对文献[20]的方法进行了改进,简化了求解零空间的过程。为提高算法性能,文献[22]使用软判决序列作为处理对象,引入对数似然系比(log likelihood ratio,LLR)[23],遍历每个码长对对偶关系进行检测,完成对信息比特和冻结比特的识别。文献[24]和文献[25]则利用极化码生成矩阵的结构性质,优化了校验向量的计算过程,提高了处理效率。
但上述方法均假设极化码的冻结比特取值为0,忽视了冻结比特可任意取值这一事实。由于冻结比特的取值不影响极化码的译码性能,编码理论研究通常假设该值为0,但在具体应用中可根据实际需要设定冻结比特的取值[26-27],以提高用户终端(user equipment,UE)检测下行控制信息(downlink control information,DCI)的速度和准确性[26],降低UE对DCI发生误检和虚警的概率[27]。另一方面,冻结比特的取值又是译码的必要信息[17]。因此,在非合作通信中,不能简单地认为冻结比特取值为0。为了能够正确恢复所传信息,不但需要对码长、码率、信息/冻结比特的位置进行识别,还要对冻结比特的取值进行估计。
针对上述问题,本文对极化码的性质展开研究,证明了当冻结比特取值不为0时,码字矩阵与生成矩阵列向量之间的校验关系与比特位类型、冻结比特取值之间的联系。在此基础上,将信息/冻结比特位的识别,以及冻结比特取值的判断,转化为一个一维三类的统计判决问题,并引入似然差(likelihood difference,LD)[7,28]构造判决统计量,检验码字与生成矩阵间的校验关系。同时,详细分析了统计量的概率分布特性,基于极小化极大概率准则给出了判决门限。最后,利用不同码字矩阵条件下等效码率与真实码率之间的关系,确定最终的识别结果,完成译码所需参数的求解。与现有方法相比,本文在保持相同计算复杂度水平且不降低识别性能的条件下,克服了现有方法无法识别冻结比特取值的不足,对现有极化码参数识别理论进行了补充与完善。
1 极化码识别基础
极化码的基础是信道极化理论,其核心是通过信道极化处理,使各子信道呈现出不同的可靠性。随着码长的增加,子信道的容量将趋近于两个极端,一部分子信道容量趋近于理想信道,剩余的子信道容量则趋近于0[17]。对于BEC,可采用巴氏参数(Bhattacharyya parameter,BP)估计子信道的可靠性[17]。对于更一般的B-DMC,如二进制加性高斯白噪声(additive white Gaussian noise,AWGN)信道,则可以利用密度进化(density evolution,DE)[29],或高斯近似(Gaussian approximation,GA)[30]方法对信道可靠性进行估计。在编码过程中,编码器选择可靠性最大的k个子信道传输信息,其余子信道传输冻结比特,冻结比特的取值保持不变。
具体而言,极化码的编码过程可用矩阵形式[17]进行表示:
ci=ui·GN
(1)
式中:ui=[ui,1,ui,2,…,ui,N]为第i个原始待编码的比特序列;ci=[ci,1,ci,2,…,ci,N]为对应的输出码字,码长为N=2n,n为正整数。GN为生成矩阵,可通过下式求得:
GN=F⊗n
(2)
GN·GN=I
(3)
ui的每个比特位可看作一个子信道。假设极化码的信息比特位序号集合为A,其补集Ac={1,2,3,…,N}/A为冻结比特位序号集合。记k=|A|为集合A中的元素数量,则极化码码率可记为ρ=k/N。
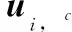
(4)
式中:GN(A)由GN中的行标号属于A的行向量构成,GN(Ac)则由GN中的行标号属于Ac的行向量构成。式(4)也可写为矩阵形式,如下所示:
(5)
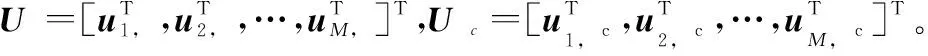
根据极化码的性质可知,极化码生成矩阵GN可以根据给定的码长唯一确定。此外,在数字通信系统中,通常线性分组码与同步码一起成帧,且有相应的帧同步码盲识别算法[31],故本文假设帧同步已经完成。因此,极化码参数识别的目的,是通过对接收序列的分析,获得码长、码率、信息/冻结比特位置集合和冻结比特的取值等译码所必需的信息。
2 基于软判决的识别原理与方法
2.1 识别原理
不失一般性,假设调制方式为二进制相移键控(binary phase shift keying,BPSK)调制,传输信道为AWGN信道。记yi=[yi,1,yi,2,…,yi,N]和ti=[ti,1,ti,2,…,ti,N]分别为ci对应的硬判决和软判决结果,满足:
ti,j=si,j+ni,j
(6)
式中:ni,j为均值为零、方差为σ2的高斯白噪声序列;si,j为BPSK调制符号,与原始码字ci,j之间满足:
si,j=2ci,j-1
(7)
利用接收到的码流序列r=[y1,y2,…,yQ]构建码字矩阵RL,设码字矩阵列数为L=l·2n,则有:
(8)

考虑码长为N=2n,码率为R=k/N的极化码。首先,在无误码条件(yi=ci)下考察码字矩阵RL和生成矩阵GL之间的校验关系。
(1) 当RL的列数等于N,即L=N时。
根据式(5),接收到的码字可表示为RL=RN=C=UGN,可得
(9)

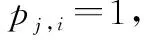
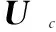
这说明,矩阵RLGL中的列向量有3种取值类型,即二进制随机序列、全部为“0”和全部为“1”。这3种情况分别对应:1)i∈A;2)i∈Ac且该冻结比特位取值为0;3)i∈Ac且该冻结比特位取值为1。因此,当L=N时,可利用上述性质,对信息/冻结比特位进行区分,并求得冻结比特的取值。同时,随机二进制向量在RLGL列向量中所占比例与码率相等。
(2) 当RL的列数大于N,即L>N(l>1)时。

(10)
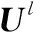
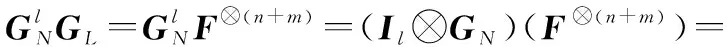
(11)
进一步可得
(12)
(13)

(14)
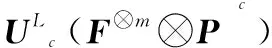
(15)
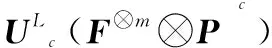
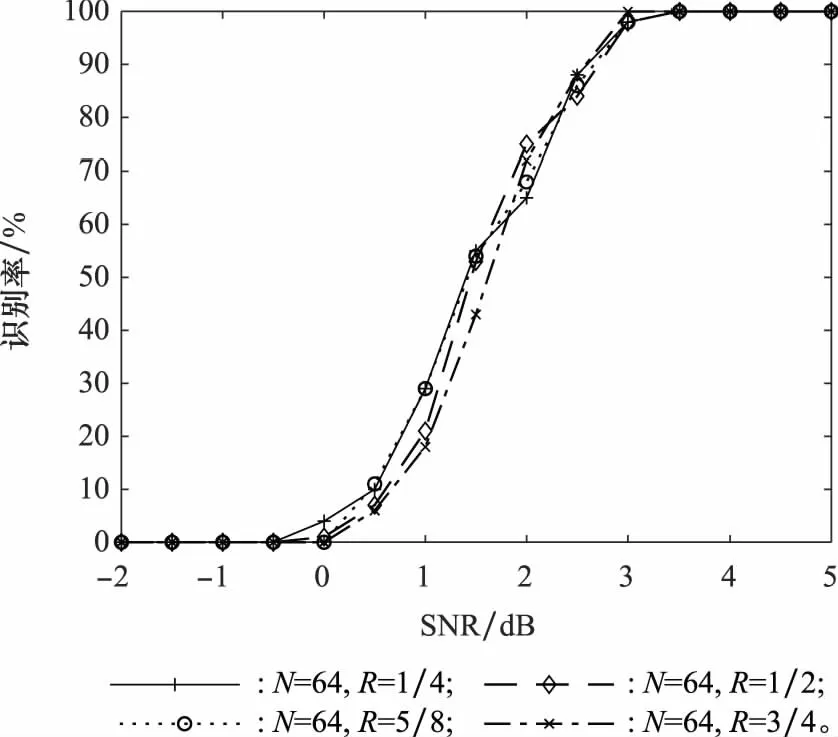
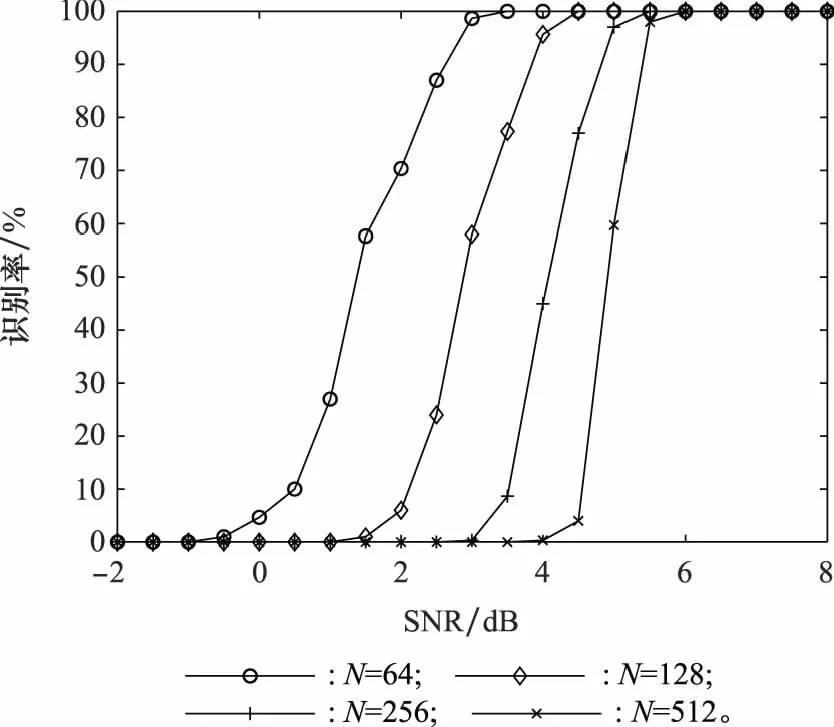
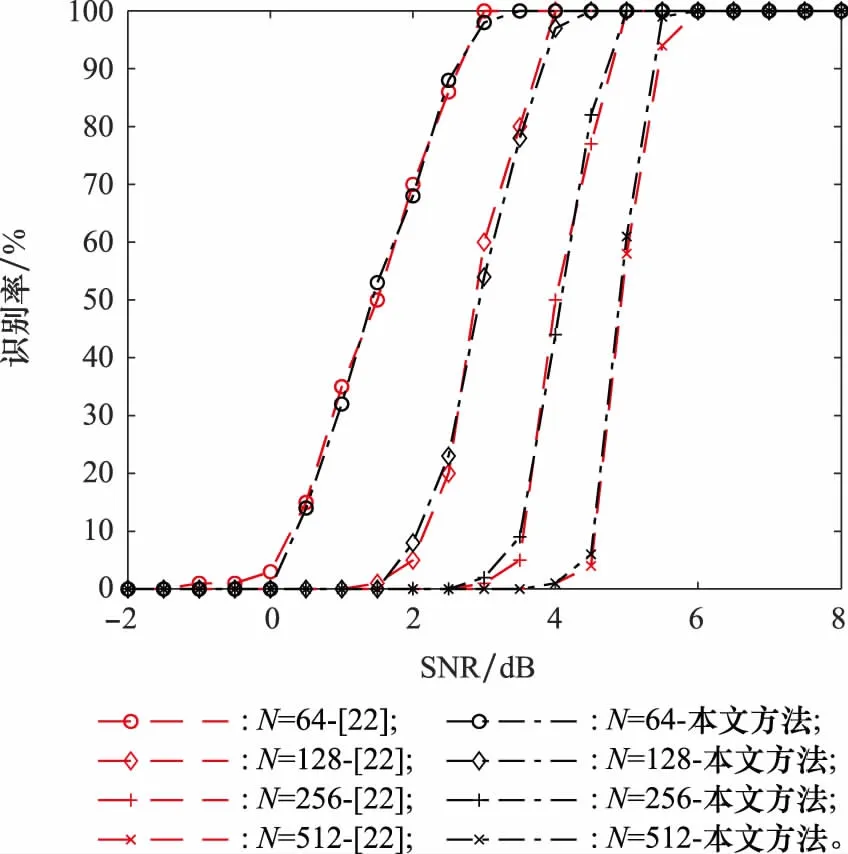
(3) 当RL的列数小于N,即L 由于信息在传输过程中受信道条件的影响,不可避免地将产生误码,此时码字矩阵RL与GL之间的关系也将受到影响,RLGL中本应全“0”或全“1”的列向量会产生一定的误码。因此,需要合理选择检验量,对RL与GL各列向量之间的校验关系进行判断。由于硬判决序列丢失了判决结果的可靠性信息,因此本文选择软判决序列进行处理,并记由软判决结果ti构成的码字矩阵为TL。 (16) 式(16)只考虑了第i个码字的LD,将码字矩阵的所有行考虑进去,则可得到平均LD: (17) H0:j为极化码冻结比特位,传输比特0; H1:j为极化码冻结比特位,传输比特1; H2:j为极化码信息比特位。 当H0成立时,意味着码字ci中下标为{pj,k}的码元中,应有偶数个码元为“1”。因此,当H0成立时,LDj的均值为 (18) 通过定义可知,函数tanh(-x/σ2)为奇函数,P(x|c=1)与P(x|c=0)互为对称函数,因此可得 (19) 将式(19)代入式(18)可得 (20) 类似地,LDj的方差为 σ2(LDj|H0)=ζwt-ζ2wt (21) 同理可得,当H1成立时,LDj的均值为 (22) σ2(LDj|H1)=ζwt-ζ2wt (23) 当H2成立时,由于码字与向量g:,j之间的正交关系随机出现,LDj的均值为 μ(LDj|H2)=0 (24) LDj的方差为 σ2(LDj|H2)=ζwt (25) (26) 从式(26)可知,不同条件下统计量均值之间的差远大于统计量的方差,因此可将本文将3类假设简化为H0和H2,以及H1和H2两个二元分类问题。设H0和H2之间的判决门限为Λ1,H1和H2之间的判决门限为Λ2。由于无法获得3类假设的先验信息,本文采用极小化极大准则求解门限Λ1和Λ2。 对于H0和H2而言,门限Λ1应满足: (27) 最终求得 (28) 同理可得 (29) 如前文所述,本文利用平均LD作为统计量,完成RLGL列向量类型的判断,并利用等效码率随码字矩阵列数变化的规律实现对码长的识别。现将算法流程总结如下: 步骤 2依次对TL和对应的GL之间的校验关系进行检验,利用GL每个列向量的校验结果判断比特位类型,以及冻结比特的取值。 本节将对本文所提方法进行仿真验证分析及性能比较,包括LD理论分布的验证,算法有效性的验证,分析接收码字数量、码率和码长对性能的影响,以及与现有算法的性能比较。 LD概率分布的正确性是判决门限求解的前提条件,本节对所求解的似然差统计模型进行验证。根据均值与方差的定义,通过仿真求得在不同假设条件下,LD的均值与方差,并与均值与方差的理论值进行对比,如图1所示,其中横轴为信噪比(signal to noise ratio,SNR)。 图1 LD统计特性验证Fig.1 Validation of the LD’s statistical characteristic 根据矩阵F⊗n的构造规律可知,其列向量码重可能的取值为{2k|k∈{1,2,…,nmax}}。仿真设定了2种码重值,分别为32、64。设定的SNR范围为-10~12 dB,步长为1 dB。从图1中可以看出,在不同假设条件下,通过仿真所求得的均值与方差和对应的理论值几乎重合,证明了本文对LD概率分布函数推导的正确性。 本节采用的极化码码率为1/2,码长为32,L的遍历范围为(2,…,512)。在SNR为5 dB的条件下,L值为32与64时,GL各列向量对应的平均LD和判决门限如图2(a)、图2(b)所示。当统计量大于门限1时,则判定其对应的比特位为冻结比特位,且冻结比特取值为0。当统计量小于门限2时,则判定其对应的比特位为冻结比特位,且冻结比特取值为1。当统计量介于两门限之间时,则对应的比特位为信息比特位。相应的判决结果如图2(c)、图2(d)所示。从图2(c)、图2(d)可以看出,当SNR为5 dB时,接收信号的误码率较低,当设定码字矩阵行向量长度为64时,平均似然差的后32位存在负值,而前32位不存在负值,与前文理论推导结果一致。 图2 n=32,SNR=5 dB条件下的算法结果Fig.2 Algorithm result when n=32 and SNR=5 dB 图3则给出了L取不同值时,所求得的等效码率。从图3可以看出,随着L的增加,等效码率不断降低。当L=32时,等效码率首次达到最低值0.5。因此,可判断该极化码码长为32,码率为0.5,识别结果与真实值一致。 图3 不同L条件下的等效码率Fig.3 Change of equivalent code rate with different L 本节将分别考察码字个数、码率、码长对算法识别性能的影响,验证本文所提算法的识别性能。 (1) 码字个数对识别性能的影响 本小节采用的极化码码长为64,码率为1/2,冻结比特为二进制随机序列。假设码字矩阵行向量的数量分别为1 000、2 000、3 000、5 000,SNR为-2~4 dB,间隔为0.5 dB,蒙特卡罗次数为200,对算法在不同码字数量条件下的识别性能进行考察。从图4可以看出,码字数量对于算法性能有较为明显的影响。码字数量增加,能够较为明显地提高算法的识别性能。这主要是因为,随着码字数量的增加,统计量平均LD与理论值的差值不断缩小,算法误判的情况也随之减少,识别率同步提高。 图4 不同码字量对算法性能的影响Fig.4 Impact of data volume on algorithm performance (2) 码率对识别性能的影响 本小节采用码长为64的极化码,码率分别设定为1/4、1/2、5/8、3/4,冻结比特为二进制随机序列。码字数量为2 000,SNR为-2~4 dB,间隔为0.5 dB,蒙特卡罗次数为200,对算法在不同码率条件下的识别性能进行考察,识别结果如图5所示。 图5 不同码率对算法性能的影响Fig.5 Impact of code rate on algorithm performance 从图5可以看出,本文算法的识别性能受码率影响较小。这是因为,极化码信息比特位的选取是根据信道可靠度依次选取的,虽然信息比特位和冻结比特位的数量随码率变化而改变,但在识别过程中需要对所有的比特位进行检验。其中,GL中码重较重的列向量对识别性能影响较大,这对于不同码率的极化码都是一样的,因此码率对算法识别的影响较小。 (3) 码长对识别性能的影响 本小节设定的极化码码长分别为64、128、256、512,码率为1/2,冻结比特为二进制随机序列。码字个数为2 000,SNR范围为-2~8 dB,间隔0.5 dB,蒙特卡罗仿真次数为200。仿真结果如图6所示。 图6 不同码长条件下识别性能仿真图Fig.6 Impact of code lengths on recognition performance 从图6可以看出,本文提出的算法具有良好的噪声适应能力。但随着码长的增加,其误码适应能力逐渐降低。产生该现象的原因主要是以下两个方面:一是随着码长的增加,单个码字中出现误码的概率随之增加,更易受到误码的影响。二是因为随着码长的增加,需要识别的子信道也变多,特别是GL中大码重列向量的增多,增加了识别的难度。因此在相同条件下,随着码长的增加,识别率越低。从识别结果来看,当SNR为5.5 dB时,对于码长为512的极化码,所提算法能够达到接近100%的识别率,说明算法具有较好的误码适应能力。 由于现有算法均假设冻结比特取值为0,只能对信息比特位和冻结比特位进行区分,而不能识别冻结比特的取值。因此,本文选择在冻结比特为0的条件下,与文献[22]所提算法进行性能比较。设定的极化码码长分别为64、128、256、512,码率为1/2。码字个数为2 000,SNR范围为-2~8 dB,间隔0.5 dB,蒙特卡罗仿真次数为200。对于文献[22]的算法,只需进行比特位类型的识别,不需要对冻结比特的取值进行判断。而本文算法仍认为冻结比特的取值未知,在识别比特位类型的同时,对冻结比特的取值进行判断。仿真结果如图7所示。 图7 不同算法识别性能仿真图Fig.7 Comparison of identification performance for different algorithms 从图7中的仿真结果来看,两个方法的识别性能相当,没有明显的差异。文献[22]的方法采用一维二类判决,本文采用的则是一维三类判决。在计算复杂度方面,本文方法每进行一次判决,多出一次门限计算和门限比较,但总体计算量在同一量级。综上所述,本文所提方法相较于现有方法,能够在相同计算复杂度水平和识别性能的条件下,适用于更广泛的应用场景。 现有极化码识别算法无法适应冻结比特不为0的场景,使用范围受限。针对该问题,本文从理论上证明了标准非删余极化码冻结比特不为0时,码字矩阵与生成矩阵之间的校验关系。在此基础上,提出了一种标准非删余极化码参数识别算法。算法引入LD构造统计量对软判决序列进行处理,将比特位类型的判断和冻结比特取值的识别转换为统计判决问题,能够有效识别信息/冻结比特位,以及冻结比特的取值。仿真结果验证了本文所提算法的有效性和对低SNR的适应能力。与现有算法相比,本文算法在保持相同计算复杂度水平且不降低识别性能的同时,弥补了现有方法无法识别冻结比特取值的不足,具有更广阔的适用范围,在实际工程中有良好的应用前景。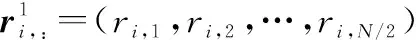

2.2 校验关系检测


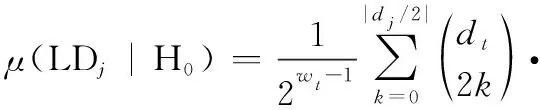
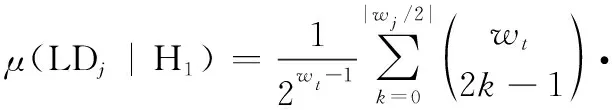
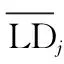
2.3 算法流程


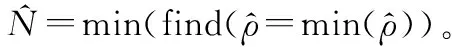
2.4 算法计算复杂度分析

3 仿真分析
3.1 统计模型验证
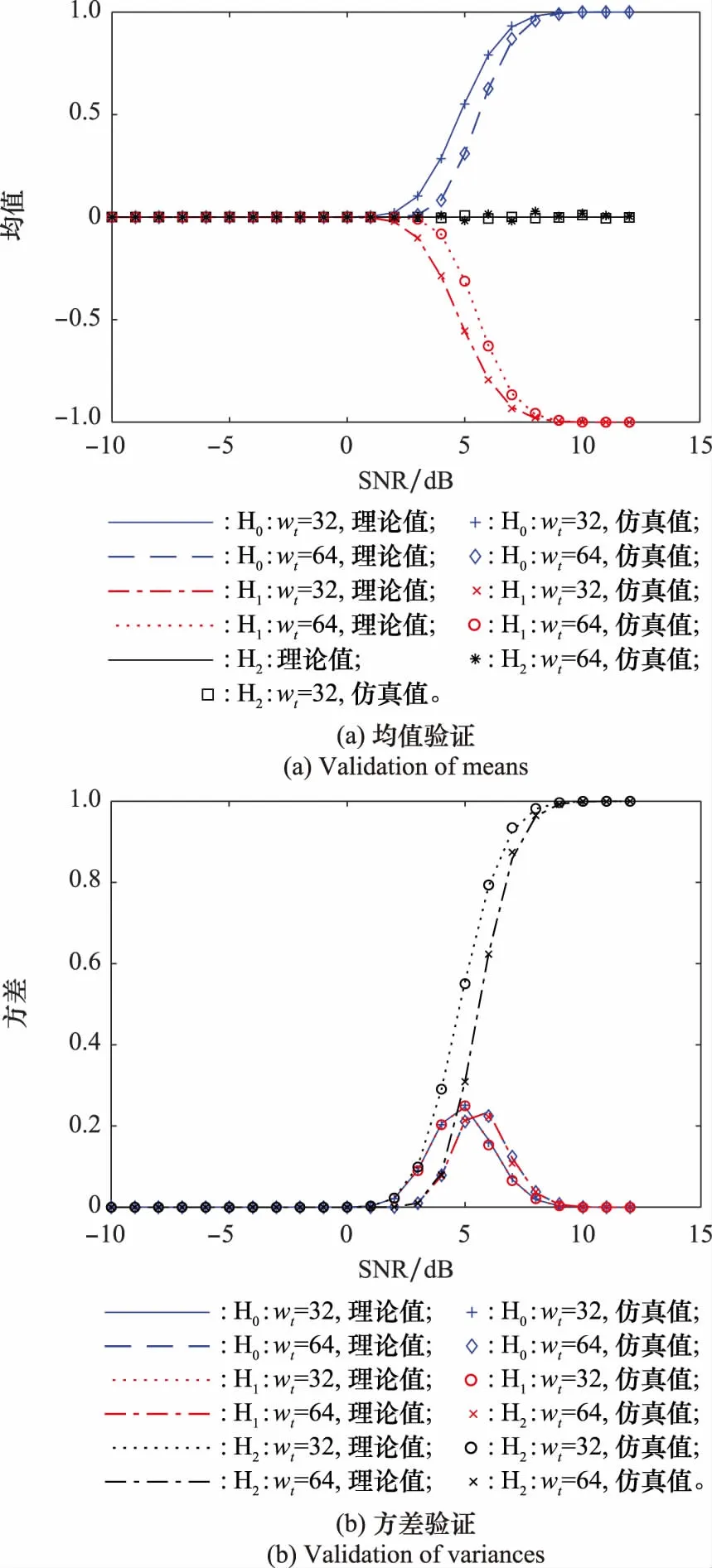
3.2 算法有效性验证
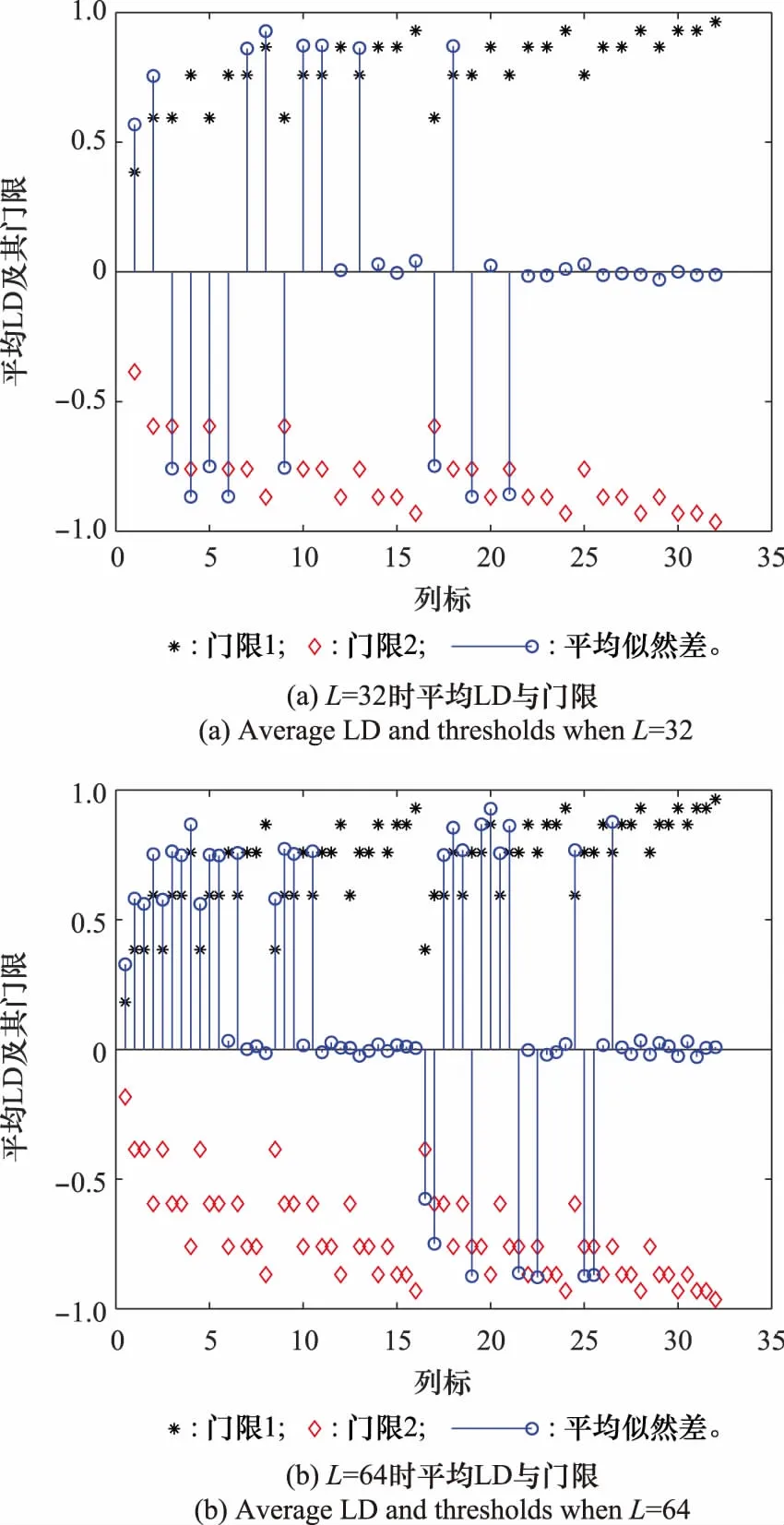

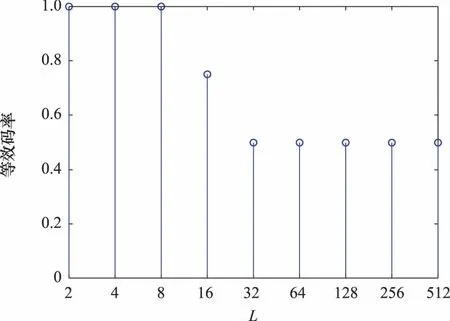
3.3 识别性能验证

3.4 性能对比
4 结 论
