基于欧拉角的李群捷联惯导误差模型分析与比较研究
2023-10-11朱天高李开龙赵仁杰
朱天高, 刘 勇, 李开龙,*, 赵仁杰
(1. 海军工程大学电气工程学院, 湖北 武汉 430033; 2. 海军工程大学舰船与海洋学院, 湖北 武汉 430033; 3. 海装驻北京地区军事代表局, 北京 100071)
0 引 言
以捷联惯导系统(strapdown inertial navigation system, SINS)为核心,其他定位系统(全球定位系统(global position system, GPS)、多普勒计程仪(Doppler velocity log, DVL)等,为辅助信息源,实时修正构成捷联惯性基组合导航系统[1-6]。对于捷联惯性基组合导航系统,组合导航模型的构建是最为核心的部分之一[7-10]。组合导航模型主要分为基本模型和误差模型,一般采用误差模型进行组合导航。误差模型的选取对于组合导航性能的影响极大,因此如何构建合适的误差模型至关重要[11-16]。
近年来,李群这一数学模型被引入惯导误差模型的构建,引起众多学者的关注[17-18]。在传统误差定义中,姿态误差定义在特殊正交群(special orthogonal group,SO(3)),而其他状态误差均定义于欧式空间中[19-20]。若将姿态、速度状态量引入一个群中,可构成特殊欧式群(special euclidean group,SE(3)),从而构建新的误差模型[21-22]。在构建误差模型时,根据误差定义的不同,可分为左乘和右乘,对于观测量也存在左不变与右不变之分[23-24]。因此,如何针对不同的观测量选取相对应的误差模型,是实现高精度组合导航的关键所在。
文献[25]提出载体系四元数误差模型,并证明该误差模型更适用于SINS/GPS组合导航。文献[26-27]提出基于欧拉角的李群左误差模型和右误差模型,证明将左误差模型应用于SINS/GPS组合导航的效果更佳。文献[28]提出地球系下的李群左误差模型和右误差模型,进行SINS/GPS与SINS/OD(odometer)两种组合导航实验,对误差模型的选取提出了有效的方法。
以上对于误差模型的应用选择均取得诸多成果,但针对基于欧拉角的两种李群误差模型的选取和适用差异性等的研究还十分缺乏。基于此,本文以SINS/GPS和SINS/DVL两种典型组合导航应用为研究对象,通过车载实验与船载实验探究李群左、右误差模型的适用性能差异,为不同应用场景的误差模型选取提供了有益的思考。
1 李群模型
定义坐标系如下:记地心惯性坐标系为i系,地球坐标系为e系,选择“右-前-上“载体坐标系为b系,计算载体坐标系为b′系,“东-北-天”地理坐标系为导航坐标系,记为n系,计算导航坐标系为n′系。
1.1 李群与李代数
李群是指具有连续(光滑)性质的群,每个李群对应一个李代数[29-31]。特殊正交群和特殊欧式群由矩阵乘法分别与旋转矩阵集合和变换矩阵集合组合,主要用来描述刚体运动,分别用SO(3)和SE(3)表示:
SO(3)={R∈SO(3) |RRT=I3,det(R)=1}
(1)
(2)
式中:R为旋转矩阵;t为平移向量。SE(3)的逆矩阵为
(3)
李代数位于向量空间,是李群对应一种结构。SO(3)和SE(3)对应的李代数分别为
SO(3)={θ∈R3,(θ×)∈R3×3}
(4)
(5)
式中:(·×)表示反对称矩阵;θ为三维的旋转向量;ξ为三维的平移向量。
李群与李代数之间的转换可通过映射实现,SE(3)和SE(3)的映射关系如下:
(6)
式中:exp表示矩阵映射,J表示SO(3)的雅可比矩阵,表示如下:
(7)
式中:a表示单位向量。
1.2 李群捷联惯导更新模型
导航坐标系下SO(3)空间中捷联惯导更新方程为
(8)
(9)
(10)
(11)

(12)
对式(12)求逆,可得其逆矩阵为
(13)
2 李群状态误差模型

2.1 李群右误差模型
李群右误差定义为
(14)

设φr为右误差模型的失准角误差,当φr取极小值时,根据李群和李代数之间关系可得[15]
(15)
(16)

分别对式(15)、式(16)求导,可得右误差模型的姿态和速度误差微分方程为
(17)
(18)
右误差位置误差微分方程为
(19)
式中:
对于惯性传感器而言,如果只考虑常值漂移与随机游走噪声,则有
(20)
(21)
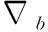
定义右误差模型状态误差为
(22)
由式(17)~式(21)可得基于欧拉角的李群右误差模型在导航系下的状态误差方程为
(23)
式中:Fr为系统矩阵;Gr为噪声转移矩阵;ηb为过程噪声向量,它们的表达式分别如下:
(24)
(25)
2.2 李群左误差模型
李群左误差定义为
(26)

(27)
(28)

分别对式(27)、式(28)求导,可得左误差模型的姿态和速度误差微分方程为
(29)

(30)
左误差模型位置误差微分方程为
(31)
定义左误差模型状态误差方程为
(32)
式中:Fl和Gl的表达式分别为
(33)
(34)
3 实验验证
3.1 李群误差模型分析与比较
在实际应用中,误差模型的选择可以根据观测值的“不变”类型来确定,“不变”观测值有以下两种定义[12-13]:
“左不变”观测:y=χb
(35)
“右不变”观测:y=χ-1b
(36)
式中:b是一个常值向量。若观测量满足式(35)“左不变”观测条件,则在组合导航模型中应用状态左误差模型会更有利,反之,如果观测量满足式(36)“右不变“观测条件,则在组合导航模型中应用状态右误差模型会更有利。

(37)
式中:bv和bp均为常值向量,速度和位置观测满足左不变观测定义。因此,GPS提供的观测信息属于左不变观测。
对于SINS/DVL组合导航系统,DVL可以提供载体系下的速度vb的观测信息。若选用速度观测y=vb,可以写成以下形式:
(38)

此外,组合导航关注的重点在于姿态,也可以从姿态误差定义角度来进行讨论。左、右误差模型姿态误差定义分别为
(39)
(40)
综上分析,SINS/GPS和SINS/DVL分别对于状态左误差模型和状态右误差模型效果最佳。下面通过跑车和跑船实验,利用实测数据比较两种状态误差模型的组合导航效果,验证实验结果是否与本节理论分析一致。
3.2 SINS/GPS组合导航实验
本节开展实验验证,主要对基于欧拉角的李群状态左误差模型、李群状态右误差模型以及传统误差模型进行对比分析。为方便后续描述,将这3种模型分别记为LSE-Euler model、RSE-Euler model和SO-Euler model,状态量的具体表示分别如下:
(41)
(42)
(43)
对于SINS/GPS组合导航系统,上文已给出姿态、速度和位置误差微分方程。量测量选择速度和位置,则3种模型的量测矩阵分别为
(44)
(45)
(46)
根据状态误差模型不同,反馈校正也有所差别,表达式分别如下:
(47)
(48)
(49)
下面进行车载实验,对误差模型进行对比分析。微电子机械系统(micro-electro-mechanical system,MEMS)/GPS车载实验平台主要包括MEMS(STIM300)、GPS接收机以及高精度的作为参考系统的光纤惯导,实验一共持续3 000 s。MEMS的性能指标如表1所示,GPS接收机的速度精度小于0.1 m/s,位置精度小于10 m,采样频率为1 Hz。组合导航系统采用GPS速度和位置作为观测量,实验过程全程都能够较好地接收GPS信号[32]。

表1 MEMS性能指标 Table 1 Specifications of MEMS
首先设置初始失准角为[1°1°3°]和[3°3°9°]进行组合导航实验,由于实验过程采用速度和位置作为观测量,因此重点比较姿态量的估计结果。图1和图2是姿态估计误差结果。由图可知,3种模型的姿态失准角均可收敛至较小范围,但在不同失准角条件下,3种模型的航向角估计误差有一定变化,纵倾角和横滚角估计误差仍几乎重合。因此,在小失准角条件下,3种误差模型均适用。

图1 [1° 1° 3°]姿态估计误差Fig.1 Estimation error of attitude on [1° 1° 3°]

图2 [3° 3° 9°]姿态估计误差Fig.2 Estimation error of attitude on [3° 3° 9°]
接下来设置初始失准角为[5° 5° 15°]、[10° 10° 30°]、[20° 20° 60°]以及[30° 30° 90°],进行组合导航实验。由上述实验可知,3种误差模型的纵倾角和横滚角的估计差别不大,故而重点关注航向角姿态估计。图3~图6为航向角估计误差。观察图可知,相比于SO-Euler模型,RSE-Euler模型和LSE-Euler模型在大失准角条件下有较大优势,可快速收敛到较小误差。尤其是从图5和图6可知,SO-Euler模型的航向角估计误差最小也是在5°以上,已无法进行组合导航,而RSE-Euler模型和LSE-Euler模型航向角估计误差仍可收敛到1°以下,且误差曲线波动较小,可进行高精度稳定的组合导航。相比于RSE-Euler模型,LSE-Euler模型的姿态估计效果整体更优,精度更高,收敛速度更快,误差曲线波动更小。实验结果表明,基于李群的误差模型的姿态估计效果优于常规的线性误差模型,LSE-Euler模型整体优于RSE-Euler模型,此实验结果与上文SINS/GPS组合导航中左误差模型要优于右误差模型的理论分析保持一致。
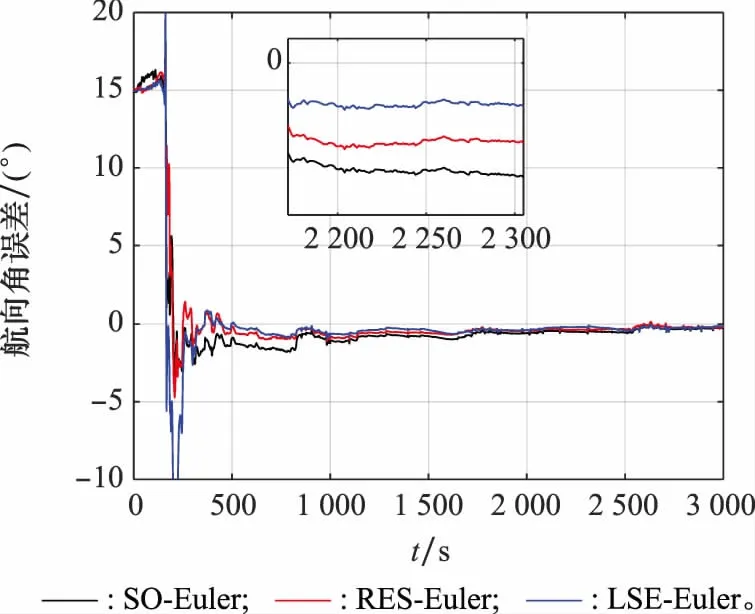
图3 [5° 5° 15°]航向角估计误差Fig.3 Estimation error of yaw on [5° 5° 15°]

图4 [10° 10° 30°]航向角估计误差Fig.4 Estimation error of yaw on [10° 10° 30°]

图5 [20° 20° 60°]航向角估计误差Fig.5 Estimation error of yaw on [20° 20° 60°]

图6 [30° 30° 90°]航向角估计误差Fig.6 Estimation error of yaw on [30° 30° 90°]
3.3 SINS/DVL组合导航实验
对于SINS/DVL组合导航系统,选取速度作为量测量,由于需考虑DVL的刻度系数因子,则LSE-Euler、RSE-Euler、SO-Euler 3种误差模型的状态量分别具体表示如下:
(50)
(51)
(52)
则3种模型的量测模型分别为
(53)
下面通过船载实验对李群左、右误差模型进行对比分析。实验数据是从一套安装有惯性测量单元(inertial measurement unit,IMU)和DVL的船载实验系统中采集得到的。表2和表3分别为IMU和DVL的主要性能指标。实验船上同时安装了一个单天线的GPS接收机,用于接收GPS数据,输出速度和位置信息,其数据更新率为1 Hz。利用IMU输出数据和GPS输出数据进行组合导航,生成参考姿态、速度和位置信息,分别作为实验中的姿态、速度和位置参考基准。船载试验在长江中进行,实验系统开机后15 min内保持系泊状态,然后试验船开始航行,航行时间大约为6 h。记录整个运动过程中的IMU和DVL的原始数据以及GPS输出的速度和位置数据。本文选取其中10 000 s船载实测数据用于组合导航仿真实验验证。

表2 IMU性能指标 Table 2 Specifications of IMU

表3 DVL性能指标 Table 3 Specifications of DVL
本实验首先在初始失准角条件下进行组合导航实验,3种误差模型的差别较小,限于篇幅原因在此不予以展示。下面主要介绍初始失准角为[5° 5° 15°]时进行的组合导航实验。姿态估计误差如图7~图9所示,3种误差模型的姿态误差估计相差较小,最终均可收敛至较小且保持稳定。

图7 纵倾角估计误差Fig.7 Estimation error of pitch angle

图8 横滚角估计误差Fig.8 Estimation error of roll angle

图9 航向角估计误差Fig.9 Estimation error of yaw angle
对于SINS/DVL组合导航而言,DVL只有速度输出,因此速度和位置的估计精度是非常重要的导航参数指标。图10和图11为东向速度误差和北向速度误差,对于东向速度误差,LSE-Euler模型的误差最大,RSE-Euler模型和SO-Euler模型的误差较小。对于北向速度误差,3种模型相差不大,基本保持一致,由此可以看出RSE-Euler模型和SO-Euler模型要优于LSE-Euler模型。图12和图13分别为纬度误差和经度误差,图14为轨迹对比图。由图可知,RSE-Euler模型纬度误差最小,SO-Euler模型纬度误差次之,LSE-Euler模型纬度误差最大。而对于经度误差,SO-Euler模型则要优于LSE-Euler模型和RSE-Euler模型。通过图14中的轨迹对比可发现,SO-Euler模型和RSE-Euler模型明显优于LSE-Euler模型,RSE-Euler模型则要略微优于SO-Euler模型。因此,由实验结果可以得出,RSE-Euler模型最佳,SO-Euler模型稍次之,LSE-Euler模型最差。故而对于SINS/DVL组合导航系统,RSE-Euler模型为最佳组合导航方式,与上文右误差模型最适合SINS/DVL组合导航系统的理论分析取得了相互印证。

图10 东向速度误差Fig.10 Estimation error of east velocity

图11 北向速度误差Fig.11 Estimation error of north velocity
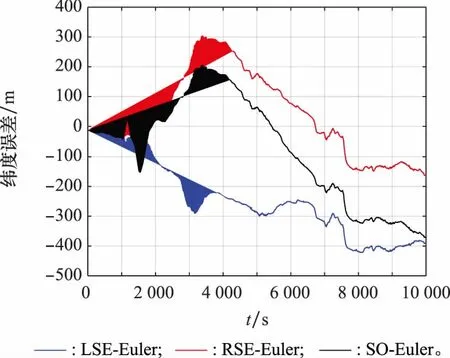
图12 纬度误差Fig.12 Estimation error of latitude

图13 经度误差Fig.13 Estimation error of longitude
4 结 论
本文对基于欧拉角的两种李群误差模型进行了比较研究,提出了针对SINS/GPS和SINS/DVL两种典型的组合导航应用的误差模型选择方案,并对该方案进行了理论分析。通过车载实验和船载实验验证了本文提出的误差模型选择方案的有效性。实验结果表明,李群左误差模型和右误差模型分别更适用于SINS/GPS和SINS/DVL组合导航系统,分别具备更好的定位效果。本文所提方案在实际组合导航系统的误差模型选择上具有较大的优势,具有良好的工程应用价值,同时也为其他组合导航模型的构建拓宽了思路。
