基于CEEMD半球谐振陀螺输出预测方法

吴宗收, 汪立新, 沈 强, 李 灿, 李文华

(火箭军工程大学导弹工程学院, 陕西 西安 710025)

0 引 言

半球谐振陀螺(hemispherical resonator gyro, HRG)作为现役陀螺仪表中精度最高的哥式振动陀螺,测量精度最高可达0.000 08°/h[1-2]。HRG结构简单,没有高速旋转的机械转子,且没有因机械摩擦而引起的陀螺漂移,除了在地面试验和储存期间器件的真空衰减会影响性能,不存在其他失效机理,因此具有寿命长的特点[3-7]。此外,HRG噪声低,对加速度不敏感,能承受大的机动过载,抗辐照能力强,有良好的抗冲击性,拥有瞬间断电工作保持能力,在空间领域受到越来越多的关注和应用[8-11]。基于HRG构建的惯性导航系统的研究和发展方兴未艾,正逐渐成为惯性技术领域的研究热点[12-16]。

随机误差是衡量陀螺仪精度的重要指标,同时也是影响惯导系统精度的主要因素之一。HRG随机误差补偿的常用方法为滤波处理,补偿结果的好坏将直接影响HRG的使用精度,因此需建立适合在线补偿的HRG随机误差模型。HRG的输出数据呈现较强的非线性和非平稳性,常用输出预测方法有时间序列分析建模预测、多元线性回归预测等。传统时间序列模型预测方法要求数据平稳或差分之后的数据平稳,且其本质上只能捕捉线性关系,该方法并不适用于HRG输出预测。本文引入组合模型预测的思想,采用互补集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)方法对HRG数据分解,得到不同特征尺度的数据序列,根据各序列的平稳性,分别应用时间序列模型预测方法与神经网络预测方法进行预测,最终得到组合预测模型。

1 CEEMD

经验模态分解(empirical mode decomposition,EMD)是一种自适应数据挖掘方法[17],能够克服由待处理数据非平稳或非线性质带来的不利影响[18-21]。通过EMD,可得到复杂信号的多个信号分量,信号分量分为本征模态函数(intrinsic mode function,IMF)和残余分量,每个IMF分量包含原信号的不同时间尺度的局部特征信号。但EMD方法存在模态混叠问题,易导致数据在被分解过程中出现重复分解等问题。集合EMD(ensemble EMD,EEMD)方法,利用附加白噪声的特性,解决了EMD方法存在的劣势,但白噪声在集合平均之后存在残留,导致重构信号的噪声不可忽略[22]。CEEMD是EEMD的改进算法,该算法分别将一对互为相反数的白噪声序列作为辅助噪声而加入原信号,解决了EEMD方法无法消除原信号中残留噪声的问题,同时减少了分解迭代次数,降低了计算成本[23-26]。CEEMD分解的具体步骤如下:

步骤 1在原信号x(t)中分别加入一对正负白噪声信号Ni(t)和-Ni(t),得到一组新的信号:

(1)

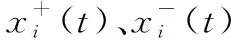
(2)

式中:cij(t)为第i次加入白噪声信号所产生信号的第j个IMF分量,当j=m时,为残差量。

步骤 3重复步骤1、步骤2P次,加入P次成对正负白噪声。

步骤 4对多组IMF分量和残差量集合平均,得到CEEMD分解结果:

(3)

式中:IMFj为最终得到的第j个IMF分量。

2 BP神经网络

反向传播(back propagation,BP)神经网络是神经网络算法中的经典算法,其误差BP算法具备自学习、自适应、可进行分布式并行信息处理的特点[27-28],网络输出可通过权值与阈值的调整从而持续逼近期望输出,在图像分析、模式识别等领域应用广泛[29-30]。

多层前向型BP神经网络的结构如图1所示。

图1 BP神经网络结构图Fig.1 Structure diagram of BP neural network

神经元在同一层内相互独立,在相邻层内保持互相连接,利用输出与期望的误差反馈给隐含层进行训练,以得到准确的输出。令输入层、隐含层、输出层的节点数目分别为m,n,l,网络输入为xi(i=1,2,…,m),输出为yk(k=1,2,…,l);wij(j=1,2,…,n)表示输入层第i个神经元与隐含层第j个神经元的连接权值,wjk为隐含层第j个神经元和输出层第k个神经元的连接权值;bj为隐含层神经元阈值。隐含层传递函数通常应用Logsig函数或Tansig函数,输出层节点传递函数选择Tansig函数或Purelin函数。

Logsig函数:

(4)

Tansig函数:

(5)

Purelin函数:

y=x

(6)

3 输出预测组合模型

目前常用的HRG输出预测方法为自回归(autoregre-ssive,AR)模型、AR滑动平均(AR moving average,ARMA)模型建模预测。由于HRG输出数据非线性和非平稳性的特点,ARMA建模需对数据进行差分与反差分处理,本质上是对差分后的HRG输出数据进行建模预测,但在实际应用时存在一定争议。BP神经网络预测模型拥有较强的非线性映射能力,但存在受训练数据复杂程度限制、收敛速度慢等问题,难以满足模型实时预测的要求。因此,在本文方法中,利用CEEMD将HRG原始输出数据分解,对得到的多个IMF分量和趋势项分别进行建模预测,具体步骤如下:

步骤 1应用CEEMD方法分解HRG原始输出数据,得到多个IMF分量与趋势项。

步骤 2对步骤1中得到的各信号分量进行平稳性检验,对平稳信号使用时间序列分析建模预测,对非平稳信号应用BP神经网络预测。

步骤 3将各预测值重组,得到最终预测信号。

算法流程如图2所示。

图2 组合模型算法流程Fig.2 Algorithm flow chart of combination model

4 算法应用与验证

采集某型号HRG输出数据。在常温环境中,固定陀螺位置,设置采样频率为1 s,采集时长为10 min,共采集HRG原始输出电压值数据600个,其中前500个数据用作训练数据,后100个数据用于验证模型预测精度。

应用CEEMD对原始数据进行分解,分解结果如图3所示。

图3 CEEMD分解结果Fig.3 Decomposition results of CEEMD

图3中,纵坐标为陀螺输出电压值,单位为V(伏特)。对图3中分解得到的各信号分量进行平稳性检验,根据检验结果,对IMF1～IMF7分量建立ARMA模型。由于ARMA模型在应用时阶次一般较低,p,q最大阶数设定为3,使用赤池信息准则(Akaike information criterion,AIC)准则确定模型阶次。IMF8分量与趋势项不满足时间序列建模要求,运用BP神经网络建模预测。

分解采集HRG的前500个原始输出序列,得到IMF1～IMF8分量及趋势项数据,按平稳性检验结果,应用表1中的ARMA模型对IMF1～IMF7分量进行预测,应用BP神经网络预测模型对IMF8分量及趋势项进行预测,各自得到预测后的100个数据。重构预测得到的多组信号,得到最终的预测结果。

表1 ARMA建模结果Table 1 Modeling results of ARMA

对重构信号后最终得到的预测数据与所采集HRG原始数据的后100个数据进行对比分析,以验证模型精度。定义预测误差百分比δ、平均相对预测误差百分比∂为

(7)

(8)

式中:yt为第t个数据的预测值;xt为第t个数据的真实值;n为数据总个数。计算各模型的均方误差(mean square error, MSE)、平均相对预测误差百分比,结果如表2所示。

表2 各模型预测结果Table 2 Prediction results of each model

为验证本文所提组合预测模型的精度,令之与直接使用时间序列分析和BP神经网络得到的预测结果相比较,对比结果见图4和图5。

图4 预测结果对比Fig.4 Comparison of prediction results

图5 预测误差百分比对比Fig.5 Comparison of prediction error percentage

由表2、图4及图5可以看出,由于HRG输出数据的非线性及不平稳性,ARMA模型对该复杂序列的预测误差较大;相比ARMA模型预测方法,BP神经网络预测模型不受该序列非线性及不平稳性的干扰,预测精度有一定程度的提升,但其预测精度仍受到序列复杂程度及网络结构选择的限制,且运算速度较慢;本文提出的组合预测模型算法利用CEEMD将陀螺原始输出序列分解以降低序列复杂性,根据各分量的平稳性检验结果,分别使用ARMA模型及BP神经网络模型进行预测,最后重构预测结果,在不过多牺牲运算速度的前提下提高了预测精度。从预测结果可以看出,该组合模型较ARMA预测模型精度高出两个数量级,较BP神经网络预测精度高出一个数量级,说明该预测模型可以较好地预测HRG输出。

5 结 论

本文通过对HRG的输出数据进行CEEMD,对得到的各信号分量分别使用时间序列分析建模和BP神经网络建模,提出了一种基于CEEMD的时间序列神经网络建模预测方法。通过与传统的时间序列建模分析方法、BP神经网络建模预测方法对比发现,本文提出的方法不受HRG输出数据具有较强非线性、非平稳性的特点影响,且模型预测精度较高。综合以上因素,本文提出的基于CEEMD的时间序列神经网络建模预测方法,为HRG随机误差预测提供了一个新的思路,具有一定的工程应用价值。