促进学生深度学习的“物质的量”单元教学——“气态粒子的那些事”教学设计

洪 璐

(合肥市第七中学,安徽 合肥 230088)

《普通高中化学课程标准(2017年版2020年修订)》中在第四部分“课程内容”主题1化学科学与实验探究中提出:了解物质的量及其相关物理量的含义和应用,体会定量研究在化学学科中的重要作用[1].由物质的量为核心概念,以摩尔质量、浓度、阿伏加德罗常数等化学概念为次要概念以及这些概念之间的相关联系,共同构成了物质的量概念体系.

因此本文对高中化学“物质的量”进行单元内容整合,指出物质的量作为一种化学计量的工具,其过去、现在和将来都体现了科学发展的进程和延续,从而确定单元主题为——发展中的化学计量.

1 单元深度学习目标

该单元的教学目标见表1.

表1 单元教学目标

2 单元教学设计——以“气态粒子的那些事”教学设计为例

环节一:探究物质体积大小的影响因素

【问题情境】根据所给数据算出对应体积,每组同学算一种物质,小组讨论,寻找体积与物质的量之间的关系.

【学生活动】学生自己操作并记录数据.

【成果汇报】1 mol任何气体,无论是纯净气体还是混合气体,在标准状况下,气体体积都约为22.4 L.注意到只要温度和压强一定时,气体摩尔体积是个定值,与气体种类无关.

【设计意图】这部分帮助学生唤起前一课时的关于物质的量和气体摩尔体积所学内容,学生通过计算数据可以直观感受到气体摩尔体积与气体种类无关,与温度和压强有关,并存在定量关系,引出下一环节的探究活动[2].

环节二:探究影响物质体积的因素

【问题引导】当温度和压强一定时,气体摩尔体积是个定值.那么固体、液体的摩尔体积有什么规律呢?

【学生活动】观察石墨烯的高分辨图像按相同比例模拟下的气体图,并从微观粒子的角度思考影响这些物质体积的因素.

【问题引导】影响不同状态下物质体积的主要因素是什么?

【交流汇报】对于固体物质而言,微粒之间排列非常紧密,微粒本身的大小远大于微粒间距,因此在微粒数目一定时,影响固体物质体积的主要因素是微粒本身的大小,而微粒间距可以忽略不计,液体物质由于和固体物质一样都是紧密堆积,因此影响液体物质体积的因素与固体物质是一样的.

【设计意图】学生通过观察固、液、气三种微观图片,体会在微粒数目相同时,微粒间距与微粒大小对物质体积的影响.这种教学情境有助于学生由宏观模型联系到化学的微观世界,便于想象和理解“影响物质体积大小的因素”.好的教学情境可以调动积极的学习氛围.

环节三:探究影响气体体积的主要因素

【问题引导】结合前面内容,影响气体体积主要因素——微粒间距,是如何受温度和压强影响?气体体积与温度、压强之间的定量关系是什么?

【学生活动】分组实验,用盖子堵住针筒出口,形成密闭体系,分别挤压和抽动活塞,观察针筒体积大小.再将针筒分别放在热水、冷水中,观察气球体积变化.

【实验展示】在探究气体体积与温度、压强的定量关系时,可以借助手持技术实验仪器,验证波义尔定律和盖·吕萨克定律.

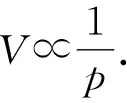
【实验2】用热水浇灌针筒外壁,使用温度传感器测量流过针筒外壁水的温度,记录针筒的刻度变化,待针筒外壁自然冷却后再记录针筒的刻度,可以得到气体体积与温度之间的关系:V∝T.

【实验3】将两个分别装有一定量的氯气和空气针筒,用带开关的转接管连接,记录气体刻度后,打开开关,观察现象及针筒刻度的变化.观察到,混合前后两端针筒的刻度读数并没有改变,说明在恒温恒压下,任何气体的微粒间距都是相同的,因此不反应的气体体积与物质的量的关系:V∝n.

【讨论汇总】从微粒角度来看,压强或温度改变,使气体微粒间距发生变化,气体体积发生改变;若温度和压强一定,任何气体的微粒间距都相同,混合气体体积可以直接加和.由此,形成数学定量关系式V∝nT/p,代入1 mol不同气体在不同温度和压强下的体积数据,得到一个常数R,形成公式pV=nRT.

【科学史展示】这个公式在1834年就被发现,称之为“理想气体状态方程”,也称克拉伯龙方程.

【问题引导】请同学们利用pV=nRT,计算标准状况下(T=273 K、p=101.325 kPa,n=1 mol,R=8.314 kPa·L3·mol-1·K-1)下的气体摩尔体积,并考虑是否只有在标准状况下,气体摩尔体积才是22.4 L·mol-1?

【学生活动】代入数据,计算出标况下气体摩尔体积≈22.4 L·mol-1,根据V=nRT/p知道,当压强和温度同时增大或减小时,V也可能是22.4 L·mol-1.

【设计意图】学生从课堂活动和生活常识粗略的了解到“压强越大气体体积越小”“热胀冷缩”等原理,而手持技术实验可以让学生更加精确地认识到压强、温度与气体体积的定量关系,从感性认知上升到理性思维,从定性研究转变到定量研究,为后面学习阿伏加德罗定律做好铺垫.通过引入科学史,带领学生循着科学家的脚步探索,让学生充分体会到科学探究的乐趣[3].

环节四:推导阿伏加德罗定律、学习阿伏加德罗常数的历史发展

【问题引导】根据公式pV=nRT,请描述T、p、V、n之间存在哪些定量关系.

【学生讨论】相同温度、压强时,气体的体积之比等于物质的量之比.

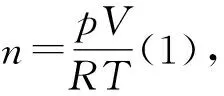
【原理揭示】阿伏加德罗定律揭示了微观原子或分子的性质与物质的宏观特性之间具有对应关系.

【问题引导】阿伏加德罗定律与阿伏加德罗常数有什么关系呢?

【科学史展示】很多人会误以为阿伏加德罗常数是阿伏加德罗本人提出的,其实不然.阿伏加德罗只提出了阿伏加德罗定律,并没有提出阿伏加德罗常数.1811年,阿伏加德罗提出,在同温同压下,相同体积的任何气体都含有相同数目的分子.

这句话启示人们,可以通过测定气体体积来间接测定气体分子数.1909年,法国物理化学家佩兰用实验证实了“分子”的客观存在,为了纪念阿伏加德罗的贡献,他测出并命名了“阿伏加德罗常数”这一名词.

【讨论汇报】阿伏加德罗常数是对阿伏加德罗定律的一个继承和证明,而这中间相隔了近百年的时间,科学发展不是一帆风顺的,也感受科学家在探索科学时的毅力与艰辛.

【问题引导】为什么人教版(2019)化学必修1中,定义阿伏加德罗常数的数值时,删除了“与0.012 kg12C所含有的碳原子数相同”这句话?

【讨论总结】科学计量标准在发展,阿伏加德罗常数如果一直依赖于12C质量的测量将永远存在误差.

【科学史展现】2018年11月,国际计量大会更改摩尔的定义,其定义将不再依赖于物质质量存在,而直接定位确定的量纲.

【设计意图】通过理想气体状态方程,逐步推导出阿伏加德罗定律及其推论,从阿伏加德罗定律的意义体会到阿伏加德罗在当时提出时的伟大贡献,但是经历了近一个世纪才被后来的科学家证明并命名出阿伏加德罗常数,让学生体会到科学的发展不是一蹴而就的,需要几代人的继承和努力[4].

【课后作业】请模仿阿伏加德罗定律,根据pV=nRT及“三同定一同”“二同定比例”的数学思想,试着推导出其他有关p、V、n、T的推论.

3 教学反思(略)