岸基GPS-R水面高反演测站时空布局优化

桑文刚,王昭然,张兴国,靳奉祥,3

(1.山东建筑大学测绘地理信息学院,山东 济南 250101;2.济南市勘察测绘研究院,山东 济南 250013;3.山东科技大学测绘与空间信息学院,山东 青岛 266590)

近年来,随着GNSS飞速发展、导航卫星资源持续丰富及应用广度和深度的不断提高,有学者提出发挥GPS全天候、全天时、高精度及低成本的特点[1],利用导航定位卫星,以及水系表面、接收机构建岸基GPS双基雷达,对提取的水面反射信号进行处理。因此,水面高测定的GPS-R理论与方法逐渐受到国内外研究者的关注。

自文献[2]提出PARIS(passive reflectometry and in-terferometry system)的概念以来,众多学者对GPS-R水面测高进行了大量研究。文献[3]利用GPS信噪比(SNR)成功反演得到海平面高度变化数据,证明了基于SNR的GPS-R反演水面高度的可行性。文献[4]则利用单台测量型 GPS接收机实现了GPS-R水面高度测量,并初步验证了其作为验潮仪的功能,这使得利用测量型GPS接收机作为岸基站点进行GPS-R水面测高成为可能。而随着算法与仪器用于岸基GPS-R水面测高的可行性被验证,该项技术被广泛应用于大坝、河流及湖泊等多种水域[5-7],并已取得众多成果。为进一步研究影响GPS-R反演精度的因素,文献[8]利用第一菲涅尔反射区限定了测站的观测范围,避免接收来自地面的反射信号;文献[9—10]分别针对海面等非平静水域及水库等平静水域,研究了卫星高度角区间对反演结果的影响。目前,对GPS-R水面测高技术外部影响因素的研究不断深入,众多学者对数据处理流程进行优化以提高反演精度。文献[11]反演了美国SC02测站长达14年的海平面变化时间序列, 其结果与验潮站数据相比,两者较差的RMS为8 cm,验证了基于GPS信噪比数据监测海平面变化的可靠性;文献[12]提出了一种自适应测站高优化方法,有效提高了GPS-R反演潮位的精度。

以上研究在分析GPS反射信号反演水面高原理与方法的基础上,在不同类型水域进行了多方位可行性验证。但基于SNR的GPS-R反演结果精度、可用性及可靠性,与观测时段内可见卫星落入指定水域方位、入射角度,以及有效弧段长度和数量密切相关。同时考虑现阶段我国大中型水库大坝、库岸边坡及海岸等周边均布设有GNSS永久观测站,为进一步提高其数据利用率,可将其作为固定岸基GPS-R水面测高观测点位进行时空属性分析,结合测区情况制定布设策略,推断最佳观测时段,有效提高岸基GPS-R水面测高的观测效率,对岸基GPS-R反演水面高度具有重要意义。本文基于SNR的GPS-R反演水面高度原理,在分析观测点位时空特性的基础上,结合菲涅尔反射区及卫星高度角区间对GPS-R观测点位进行定量分析,以此制定GPS-R观测点位时空布局优化策略;并通过对临时测站与长期测站的仿真及实际观测验证该策略的可行性。

1 基于反演事件时空优化策略

1.1 GPS-R水面测高原理

如图1所示,岸基测站接收到由卫星直射和经水面反射在天线相位中心叠加而形成的复合信号[13-14]。复合信号会随着GPS卫星升降、水面高度或粗糙度变化而产生波动,导致接收的信噪比等观测量在振幅和频率上发生改变。为了有效提取水面高等水系属性,反演算法通常采用信噪比数据,基于多项式拟合或小波分析等去除趋势项方法,过滤观测时段复合信号中的直射成分后,获取包含反射面属性信息的信噪比残差序列为

图1 岸基GNSS-R水面反演

(1)

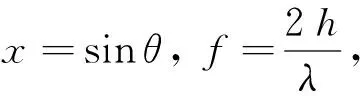
δ(SNR)=Acos(2πfx+φ)

(2)

由于信噪比残差序列相对于自变量sinθ是非等间隔采样,需利用Lomb-Scargle算法提取其主频f,求得天线相位中心至水面的垂直高度h为

(3)

为有效利用以上原理进行水面高度反演,首先应合理选择测站位置,以保障最大限度获取落入指定水域内的卫星弧段数量及长度,并根据水面设定卫星高度角范围划分上升及下降弧段。此外,还应兼顾接收机端收到的卫星直达与水面反射叠加而成的信号,强度会随卫星反射点在水面的轨迹变化而增减,定义潜在可用于水面高度反演的事件,并利用其进行最佳测站位置及观测时段的优化选择。

1.2 反演事件

如图2所示,在由GPS卫星T、水面S及接收机R构成的双基雷达中,水面反射点的位置会随卫星升降及其轨道运行而变化,在水面形成反射点轨迹。根据惠更斯-菲涅尔定理[15],以卫星信号发射端T与接收机镜像点R′为焦点形成的椭球体,在水面S相交形成多个以反射点为中心的椭圆区域F。其中,反射信号主要来源于最中心的椭圆区域,被称为第一菲涅尔反射区[16]。

图2 菲涅尔反射区

由于第一菲涅尔区中的反射信号能量更强,因此可根据接收机相对于水面方位角范围,确定测站的有效反射区α反射,公式为

α反射={α|αFresnel∩α水面}

(4)

确定测站有效反射区后,根据相关研究成果[5,9-10],对水库等相对平静水面可选取高度角5°～25°,对海面等非平静水面选取高度角5°～12°进行观测时段有效弧段(ARCi)提取,公式为

ARCi=(α反射,β)i

(5)

式中,β为高度角区间;i为某一卫星。

综上所述,在图1的卫星、反射水面及接收机之间所形成的有效反射区范围内,将满足反演所需高度角区间的上升或下降弧段定义为一次反演事件,可表示为

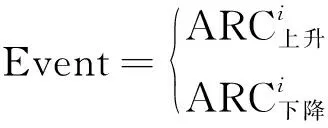
(6)

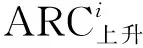
1.3 测站时空布局优化策略

考虑到导航卫星星座结构设计,尤其是轨道倾角及数量的影响,在同一测区内,测站获得的低高度角卫星弧段数量会随其观测方位及观测时间的不同而变化。针对这一特性,本文提出一种基于反演事件的岸基GPS-R观测点位时空布局优化策略,步骤如下:

(1)根据测区条件,选择若干备选测站,绘制第一菲涅尔反射区,并通过与测站周围环境相结合,设置观测方位,确保区间内反射信号全部来自水面。

(2)根据测区水面情况,选择适宜的高度角区间并根据观测需求划分时段,统计备选测站及其各时段内的反演事件数量。

(3)对比各备选测站及其不同时段内的反演事件统计数据,以事件数量为首要依据确定最佳设站位置与观测时段。

2 仿真分析

为验证基于反演事件的GPS-R测站时空布局优化策略的可行性,以图1为例,模拟位于北半球的平静水面并设定位于水系东、南、西、北处的4个仿真测站进行仿真试验,其测站高度均为2 m。

首先按照表1的参数,在图3中以不同灰度按照5°高度角为间隔,绘制各测站所有可见星下呈狭长椭圆状分布的第一菲涅尔区。可知,随着卫星高度角降低,第一菲涅尔区的覆盖范围逐渐增加,根据空间菲涅尔区模型,还可通过适当增加测站至反射面的垂直距离进一步扩大反射区范围[17]。此外,由于GPS卫星轨道倾角及轨道高度等星座结构因素,导致E、W测站第一菲涅尔区呈对称分布,而S测站相较于N测站存在一处约为60°的扇形空白区,造成其第一菲涅尔区域面积明显少于N测站。

表1 反演事件仿真点位主要指标参数 (°)

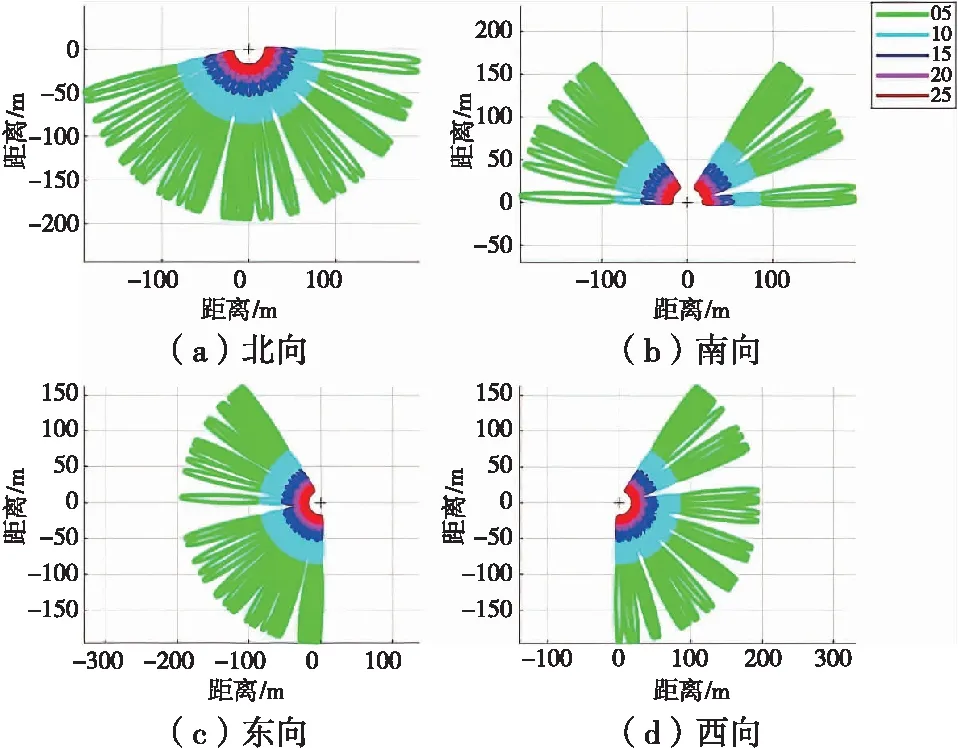
图3 各仿真点位第一菲涅尔反射区分布

在各仿真测站第一菲涅尔区确定的有效反射区内,根据式(6),以5°～25°高度角区间,按照每4 h统计一次的方法,统计1 d内各仿真测站反演事件(见表2),并同步绘制半圆周辐射面反演事件分布(如图4所示)。在半圆周辐射区域中,反演事件均以环状分布,如图4中红色表示部分。其中,E、W测站与图3中第一菲涅尔区分布一致,反演事件呈对称分布,N测站所观测到的反演事件是连续且均匀的,而S测站同样受GPS星座结构影响,被空洞分割成对称分布。由表2统计数据可以明显看出,N测站受北方空洞影响,导致其反演事件覆盖范围大于其他测站,反演事件总计达到55个。而E、W测站反演事件总数相同,但各时段反演事件数量略有差异,因此在非长期观测时,选取最优观测时段是必要的。表2展示了各时段反演事件分布,其中0:00—4:00 h及20:00—24:00 h时段的反演事件数量相对较多,其余时段内的反演事件数量大致相同。

表2 各仿真点位及其不同时段反演事件数量 个

图4 仿真点位反演事件分布

考虑地面用户观测到的GPS卫星运行周期约为23 h56 min,因此在水系不同方位反演事件时空分布呈现一定的规律性,图5(a)为4个测站1个月仿真结果,各测站天反演事件总数基本维持不变,且“北多南少,东西一致”的规律更清晰。但由于GPS卫星运行的周期规律,反演事件都会较前一天提前4 min出现,由于本次仿真1个月数据,通过绘制N测站反演事件径向堆积图,可看到图5(b)中经过30 d累积后,反演事件会提前2 h出现。

图5 1个月各仿真测站反演事件时空分布统计

3 反演事件有效率试验验证

根据本文对反演事件的定义可知,反演事件仅是统计的潜在可用于计算水面高的有效弧段数据,在实际应用中,由于反演事件对应信噪比数据会受到诸如地面反射干扰或物体遮挡等多种外界因素影响,导致反演事件中仅部分能够得到有效结果,因此需进一步验证反演事件的有效率。在上述仿真试验基础上,选择济南卧虎山水库进行验证。因该水库由坝体向东纵深,最终选择3个测站架设接收机进行试验,如图6所示,设置1 s采样率,采样时间为UTC时间2021年10月12日8:00—12:00。其中,测站1与测站3分别位于水库西侧与北侧,而位于东南方的测站2视野开阔,能够兼顾南站及东站的观测方向,使得实测观测方位与仿真测站保持一致。采样时段库区水面较为平静,因此卫星高度角区间均设定为5°～25°。结合各测站有效反射区,表3为其相对应的方位角观测区间。

表3 实测点位观测信息 (°)

图6 试验测站分布

首先,绘制采样时段3测站反演事件分布,如图7所示。红色线段表示反演事件,测站2西向与测站3获得的反演事件数量均为6个,测站1与测站2北向分别为4个和3个,其数量分布规律与仿真结果相同。

图7 采样时段3测站反演事件分布

同时,利用反演事件对应数据去除趋势项及频谱分析等处理后得到反演结果,但由于实际观测时,测站周围存在水面以外的反射面及遮挡,导致实测反演结果仅部分有效,为进一步判断GPS-R最优观测点位,本文在反演事件数量对比的基础上,对反演事件有效率进行分析。图8展示了各实测点位反演事件的有效率,以及其对应方位的仿真点位反演事件数量的对比。可以发现,在反演事件数量相同的南向与西向测站中,南向测站的数据有效率远大于西向测站,达83.3%。

图8 8:00—12:00时段仿真结果与实测结果对比

综上分析,基于反演事件的GPS-R测站时空布局优化策略在仿真测试与实测验证中,表现出良好的一致性与可靠性。其中,测区北处反演事件数量更多。同时,实测结果表明,测区北处反演事件有效率也高于其他测站,从而进一步验证了通过优化测站位置及时段选择,在确保反演事件数量的前提下,能够有效提高反演结果的有效率。

4 结 语

本文在岸基GPS-R反演水面高度应用中,基于反演高度算法核心,综合菲涅尔反射区及卫星入射角度,提出了反演事件这一概念,用于量化分析GPS-R观测点位,并以此制定了测站时空布局优化策略。通过仿真分析发现,北半球测站在一天中反演事件空间分布呈现“北多南少,东西一致”的规律,北部测站较南部测站反演事件高于34%,因此,用户在设站时应优先选择水系北端,东西次之,并尽量避开南部。由于受GPS卫星运行周期的影响,测站的反演事件也呈现周期性,可通过预报反演事件获取测站最佳观测时段,并根据其周期进行动态调整,从而全面优化GPS-R测站最优时空范围,且通过某水库岸基实测数据进行反演事件有效率验证分析。结果表明,反演事件最多的测站有效率同样高于其余测站,从而验证了开展GPS-R观测点位时空布局优化研究,能够有效提高观测效率并优化GPS-R技术反演水面高度的应用作业流程,从而进一步推动该项技术由理论研究向实际应用转变。