预应力锚索抗滑桩减震外锚结构振动台模型试验研究

2023-10-10蒋良潍张瀚文葛学军

振动与冲击 2023年18期

杨芸, 蒋良潍, 罗强, 张桐, 张瀚文, 葛学军

(1. 西南交通大学土木工程学院,成都 610031; 2. 西南交通大学高速铁路线路工程教育部重点实验室,成都 610031;3. 中铁二院工程集团有限责任公司,成都 610031)

为克服普通悬臂桩在地基岩土性质较差时易出现的整体倾覆破坏,在桩顶设置锚索使抗滑桩转变为上部铰支,下部近似弹性固结的简支梁式受力模式[1],锚索-桩身-地基共同协调受力以增强稳定性。锚索桩结构发挥承载作用的关键在于锚索的有效性,内锚头依靠砂浆与孔壁黏结保持稳定,易破坏失效且可控性较差,特别在高烈度地震区,地震波往复作用下锚索拉力急剧增长,应力幅较大时易出现疲劳破坏,“5.12”汶川地震实震表明,锚索存在因受力过大而在锚头处被拉断的震害形式[2]。因此锚索桩抗震设计的重点在于改善锚索受力。

由于受力模式复杂,预应力锚索桩的内力计算尤其是地震动力响应的理论分析成果[3-5]还较少,模型试验和数值模拟能直观观测试验现象及考察多种因素的影响关系,常作为研究锚索桩动力特性的相互验证手段。张朋[6]、武志信[7]分别利用离心振动试验和大型振动台试验探索了锚索桩的地震动力特性,并利用FLAC3D和ABAQUS软件建立数值模型进行验证。动力响应规律研究可为锚索桩抗震设计的改进提供参考依据。

目前抗震优化方案主要分“抗”和“消”两种思路。前者针对预应力大小、锚索位置、桩间距、锚索排数[8-9]等结构参数进行优化以增强抗震能力。但因为强震具有不确定性,“抗”的方式在预计效果和经济性方面仍存在一定问题。以“消”为主的减震优化代表措施为应用缓冲材料[10]和设置消能装置。建筑抗震领域常采用隔振器[11]和阻尼器来减小地震响应,隔振器一般利用弹性支座变形来减弱传入结构的振动,阻尼器则是消耗能量抑制振动;翁大根等[12]将位移相关型和速度相关型消能装置共同简化为层间弹簧-阻尼串联模型并讨论了各参数的合理取值范围;邹立华等[13]针对高层建筑基础设计了桩底铰支、桩顶串联弹簧的柔性桩消能隔震模型,得出增大阻尼对振动控制效果影响不大。目前部分研究将减震消能装置引入了支挡抗震,陈艺文[14]建立了设置弹簧的锚索支护边坡有限元模型探讨了地震下锚索轴力的改善作用;针对预应力锚索抗滑桩,冯帅等[15]设计了在桩顶锚头处设置弹簧、桩后放置EPS(expanded polystyrene)板的优化措施,通过振动台试验分析桩顶变形及墙背受力,但未细究锚索轴力这一关键承载响应。

为避免锚索桩地震下因锚索失效转变为危险的悬臂体系,设计在外锚头处串联缓冲弹簧的消能装置并开展锚索桩支挡边坡振动台模型试验,对比分析设置弹簧对桩后土体加速度、桩身外倾角及锚索轴力的影响,根据轴力幅值变化及疲劳损伤计算结果评价锚索减震效果,运用傅里叶变换分析锚索轴力响应频谱表征的能量减载特性,为锚拉支挡结构抗震设计与结构改进提供参考。

1 振动台模型试验设计

1.1 工程对象与模型概化

依托工点为西南山区交通廊道高烈度地震区某铁路拟建段路堑边坡,双线铁路采用半路堑通过坡脚覆盖层。边坡整体坡度为15°～30°,处于自然稳定状态,路堑切坡后高差为20～30 m。覆盖层为黏土堆积,内部间杂碎块石,孔隙水不发育,厚度10～15 m;下伏基岩主要为泥岩夹砂岩,隔水性能较好,裂隙不发育,坡度约为35°～40°。

工程设计方案选用锚索抗滑桩进行路堑边坡坡脚支挡,桩身总长H=18 m,截面尺寸2 m×3 m,采用C30浇筑,其中悬臂段长10 m,埋置段长8 m,桩底嵌入平缓段基岩约1 m,锚固形式为铰支;锚索采用 6 束Φ15.2 mm钢绞线制作,总长30 m,自由段长25 m,锚固段长5 m,下倾角30°。经简化后拟定概化原型边坡路堑总高差为20 m,桩顶以上坡高为10 m,坡比1∶1.25。试验设计前,建立ABAQUS有限元模型对结构受力响应进行了初步分析,以指导模型结构件元器件的选型与布设。

1.2 试验设备及模型相似律

模型试验采用ANCO公司生产的电液伺服单向地震模拟振动台,台面尺寸3.0 m×3.0 m,峰值水平加速度1.5g,最大位移±10 cm,最大抗倾覆力矩300 kN·m,复现频率范围0.1～50.0 Hz。

台面固定有效尺寸为2.52 m×1.28 m×2.00 m(长×宽×高)的刚性模型箱,长边平行于振动方向。模型箱骨架以方钢管焊接而成,两端为加肋钢板形成半封闭式结构以便模型填筑。为便于直接观测模型,模型箱侧面采用厚10 mm透明有机玻璃封闭。为避免边界效应带来激振反射[16],在加肋钢板内侧布置厚5 cm的聚苯乙烯土工泡沫板以形成柔性边界。振动台及模型箱实物如图1所示。

图1 振动台及模型箱Fig.1 Overview of shaking table and model box

模型试验相似律是结构响应能否合理复现的关键,为满足几何、运动和动力相似,选取长度、加速度、材料密度作为基本量纲。结合模型箱和原型边坡尺寸确定模型几何缩尺比Cl=15,考虑地震角相等及控制材料密度与原型基本一致,取水平地震加速度Cα=1,材料密度Cρ=1。为避免无法同时满足所有参数相似,分别针对支挡结构、边坡土体及加载地震动三部分开展相似律分析。其中,在设计地震波时间相似比Ct时,为弥补原型和模型因自重应力不同引起的模量差异,引入Hardin等[17-18]提出的模量修正原理,考虑砂土剪切模量与应力水平的非线性关系。

物理量的相似关系式和相似常数基于前述讨论据量纲分析法导出,如表1所列。

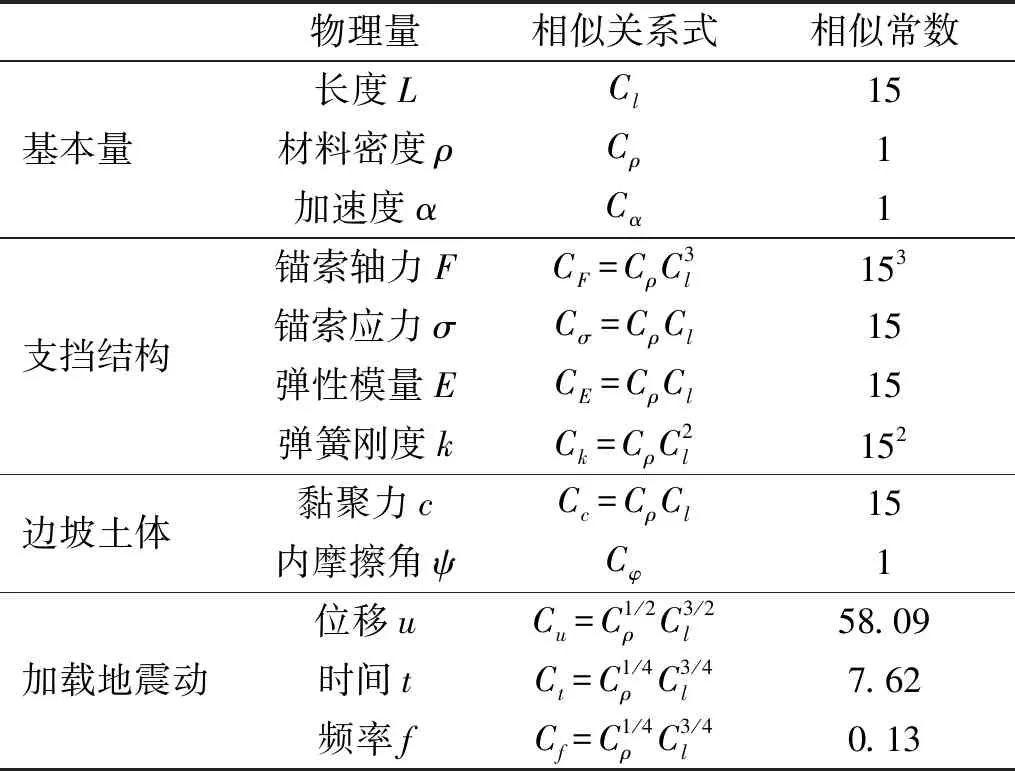
表1 振动台模型试验相似律Tab.1 Similarity law of shaking table test

1.3 模型尺寸及材料设置

1.3.1 模型总体设计

模型主体由锚索、抗滑桩、消能部件、基岩(地基)及边坡组成。总尺寸为2.52 m×1.28 m×1.95 m(长×宽×高),桩后边坡坡比1∶1.25,模型结构如图2所示。为实现桩底铰支形式,采用将抗滑桩浅置于与台面刚接的凹槽内进行模拟;桩顶的外锚头处,锚索与以弹簧为主要元件的消能部件串联形成弹性铰支约束。

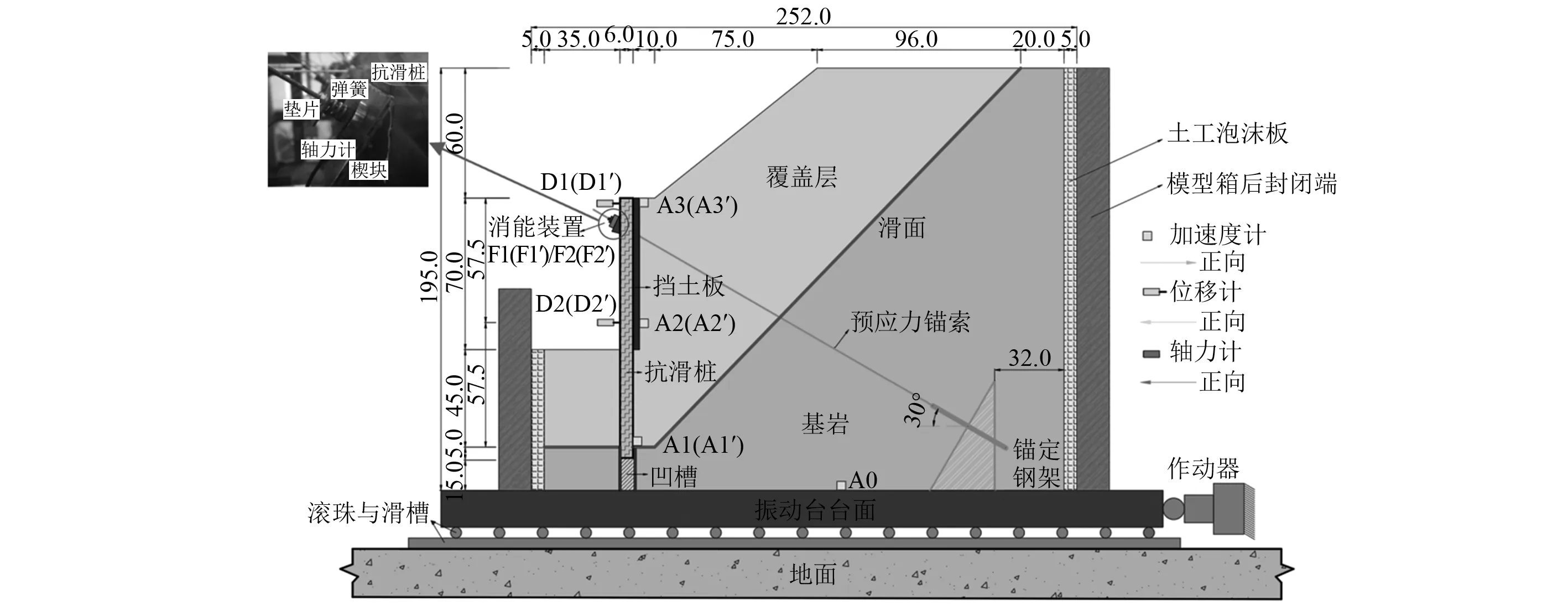
图2 模型结构设计与测点布置(cm)Fig.2 Shaking table test model design and layout of measuring instrument schematic(cm)

为满足最小桩间距[19]和原型相似比要求,模型在宽度方向设置4根锚索抗滑桩,设定桩间净距为23 cm,与模型箱边壁净距13.5 cm。同时,为对比设置弹簧与否的地震响应差异,以模型箱宽度中心为界将模型分为设置弹簧消能部件的试验桩与普通锚索桩进行对照分析。按表1中轴力相似律确定模型锚索预应力为266 N,对应于原型的900 kN。

1.3.2 锚索及消能部件

模型锚索采用直径6 mm圆钢,总长2 m,锚固角度30°,内端与嵌在基岩内部、焊于模型箱底板的锚定刚架相接,外端与外锚头连接。为减小锚索自由段与土体摩擦,选用PVC(polyvinyl chlorid)管进行套管;在圆钢外端攻丝形成螺纹,旋转螺母以控制预应力幅值。

锚头消能装置实际是建立弹簧-锚索的串联体系,通过加入弹簧这一简单缓冲元件来降低锚索刚度,锚头模型如图3所示,包含螺旋弹簧、上下垫片、轴力计、螺母、套管和楔块。

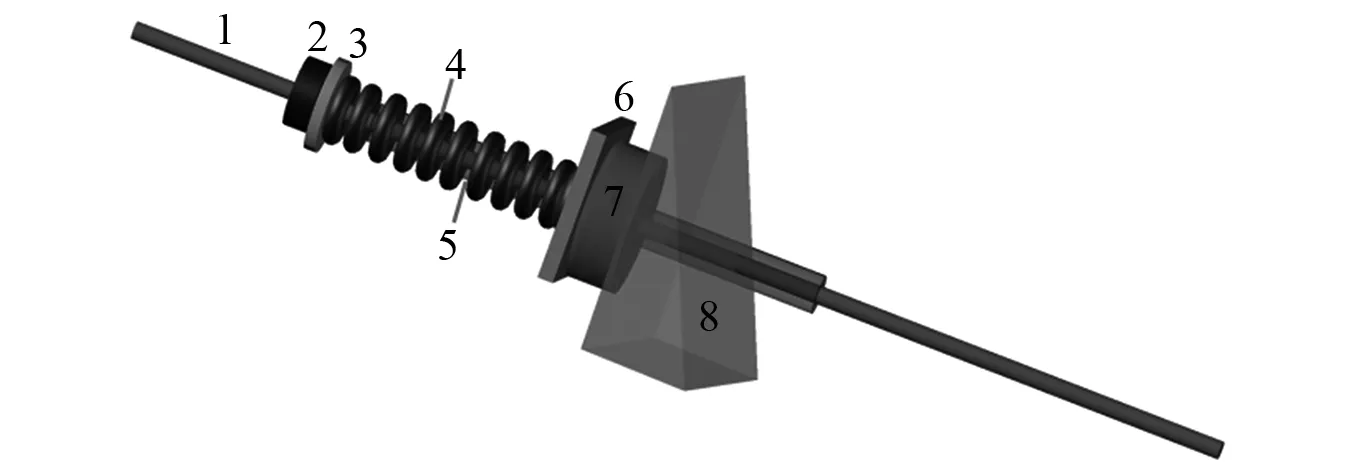
1. 锚索; 2. 螺母; 3. 垫片1#; 4. 弹簧; 5. 套管; 6. 垫片2#; 7. 轴力计; 8. 楔块。图3 试验模型消能锚头设计Fig.3 Buffer anchor head design

根据前期数值模拟结果结合相似律,拟定模型弹簧刚度440 N/mm,最大行程25 mm;楔块贴附于桩身,作用为调整角度,保证承力部件与锚索垂直;已有研究多采用应变片测量锚索轴力,但由于圆钢直径仅为6 mm,贴片难以牢固,选用微型穿心式荷载传感器以监测轴力动态变化,其前端为受力面、后端由楔块支撑,保持与锚索垂直;弹簧两端均设置刚性垫片,垫片1#为螺母垫片,垫片2#为轴力计垫片,尺寸略大于轴力计受力面以避免荷载偏心;考虑到攻丝螺纹与其他部件在震动过程中易出现卡滞,影响弹簧变形和轴力传递,设计一直径稍大于圆钢的光滑空心管套置于螺纹段外部。当锚索受拉时,螺母反力依次通过垫片1#、弹簧、垫片2#传至轴力计受力面,利用动采仪记录轴力响应。

1.3.3 桩板墙结构模型

桩板墙由抗滑桩与悬臂段桩背挡土板构成。锚索受力响应为试验关注重点,应避免桩身在试验中出现破坏,模型桩选用方钢管制作,长120 cm,其中悬臂段70 cm,锚固段50 cm,为保证桩身刚度与工程设计近似,取方钢管截面尺寸为8 cm×6 cm(迎土面宽×侧面宽),壁厚δ=3 mm。

安装抗滑桩前,在桩身平面位置对应的模型箱底固定尺寸略大于桩身截面的凹槽,高度为20 cm,抗滑桩桩底插入凹槽5 cm以形成桩底铰支条件;为避免内锚失效影响锚索受力,在圆钢内端固定锚定刚架以保证其牢固连接;桩间挡土板用厚3 mm 钢板制成,设置于桩背,防止桩后土体从桩间挤出。

1.3.4 基岩与边坡材料制备

基岩要求具有良好的承载能力且能在振动条件下保持完整性。以天然河砂作为基材,掺入一定量粒径约1～2 cm粗骨粒优化级配,加入适量黏土以增强材料黏结性,掺配少量石膏和5%的水泥使材料在短期内可具有较高强度。通过调节重晶石粉控制容重,最终确定基岩夯实后密度为2.3 kg/cm3,与原型工点基本一致,质量配合比为河砂∶石膏∶黏土∶重晶石粉∶粗骨粒∶水泥∶水=5∶2.5∶3∶4∶1∶0.8∶1。

覆盖层模拟天然堆积体,质量配合比河砂∶黏土∶重晶石粉∶水=7∶4∶2.5∶1, 夯实后密度为1.8 kg/cm3。材料物理力学性质如表2所示。为模拟基岩-覆盖层间潜在滑移面,在土-岩交界处铺设一层聚乙烯塑料薄膜,经摩擦因数测定原理测得摩擦角约为23°～25°。

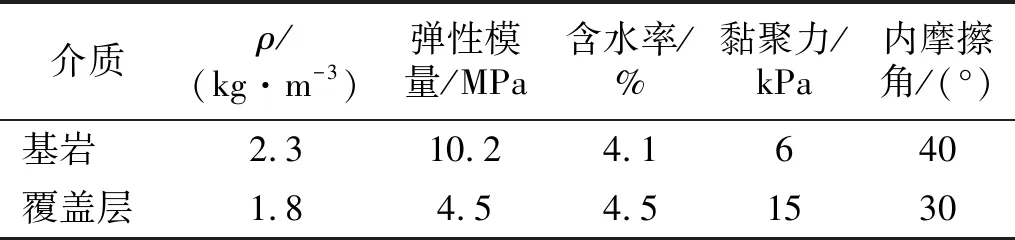
表2 边坡模型材料参数Tab.2 Parameters of slope model materials

基岩及覆盖层土体均采用分层填筑,每层压实高度15 cm,为使层间连接紧密,填筑前进行刮毛和洒水处理。边坡土体每层水平铺设蓝色染色砂条带,以便观测地震引起的边坡破坏特征及破裂面位置,填筑完成的模型如图4所示。

图4 模型填筑完成实物Fig.4 Physical model of shaking table test

1.4 测试元器件布设

如图4(a)所示,左侧两桩为普通锚索桩,右侧两桩为弹簧锚头桩,两种桩型以镜像方式布设传感器。由于边桩与模型箱侧壁距离较近,存在一定边壁效应,数据准确性应低于中桩,因此采集两型中桩的锚索轴力、加速度、位移数据进行对比,传感器布置详见图2。同时,为提高轴力数据可靠性,四桩外锚头处均加设轴力计以进行平行测试。

试验共设置7支量程为±2g的单轴电容式加速度计(CS-LAS)。A0固定于振动台台面用于采集实际加载波形, A1,A2,A3埋置于弹簧锚头中桩的桩后土体内,紧贴桩背并沿高程大致均匀分布,分别纪录桩底、1/2桩身及桩顶加速度时程;A1′,A2′,A3′布置于普通锚索中桩对应位置处。加速度计预先固定于木质衬板上,在埋设点经水准和方向校正后进行覆土,保证振动过程中测振轴与振动方向平行。

为探究锚索桩在地震作用下的位移及外倾趋势,共设置4支量程为100 mm的动位移计放置于桩身前端,探针与桩身保持垂直。D1,D2分别测量弹簧锚头中桩的桩顶和1/2桩身处动位移; D1′,D2′对应普通锚索中桩。

锚索轴力是试验关心的重要数据,根据数值模拟相似律确定测力量程,选用4支量程2 kN的穿心式荷载传感器布设于外锚头处楔块前端。F1,F2用于监测弹簧锚头中桩、边桩轴力变化;F1′,F2′记录普通中桩、边桩。

物理量方向规定参见图2,为使传感器正值体现抗滑桩处于惯性力、位移朝向临空面的危险状态,取定加速度方向为朝坡体内部为正,位移以背离土体运动为正,锚索受拉为正。

1.5 地震动加载

输入地震波采用某交通廊道地震安评典型人工合成波(时长55 s)及汶川地震强烈时段(时长30 s),基线修正后的人工合成波加速度时程曲线和Fourier谱如图5(a)、图5(b)所示。按时间比尺Ct=7.62压缩后两种波形持时分别为7.22 s,3.94 s。

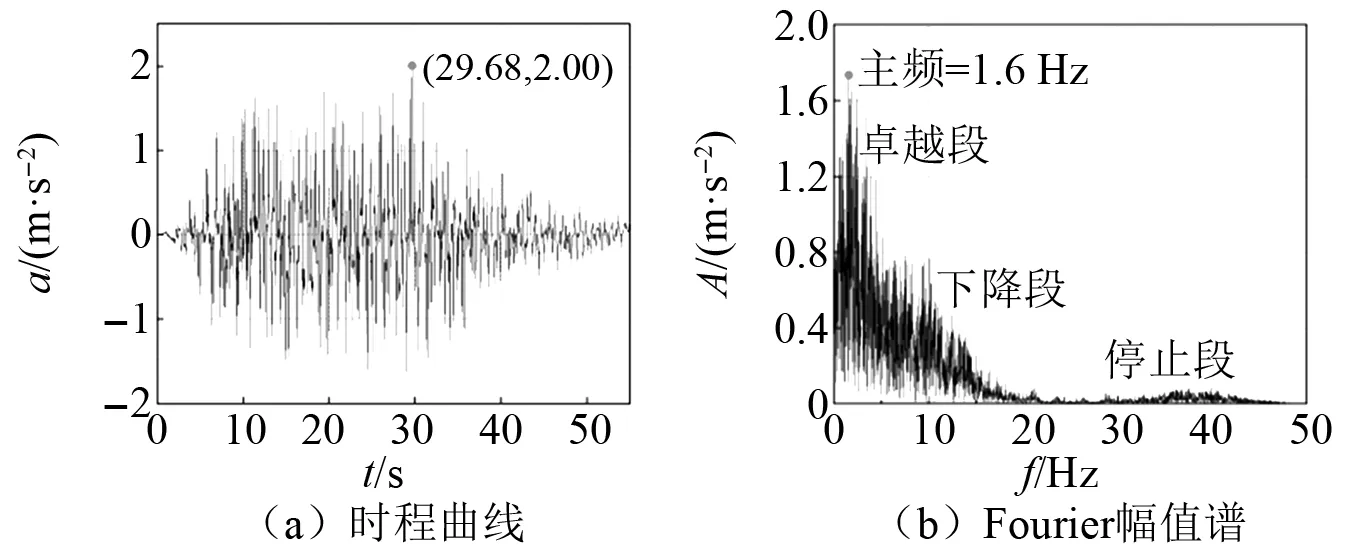
图5 人工合成波输入地震动Fig.5 Artificial seismic wave

振动台系统最高可用频率f=50 Hz,取采样时间间隔为1/50=0.02 s;为尽可能避免模型反复振动提前破坏,地震动按峰值加速度0.2g,0.4g,0.6g的顺序依次施加,分别模拟小、中、大3级地震强度,同一量级下两种波形穿插进行,共输入6组地震波,利用动态采集仪记录加速度、位移、锚索轴力响应。

2 加速度与位移响应

2.1 水平加速度响应特性

为探究设置弹簧对桩后土体加速度的影响效应,将两种外锚头抗滑桩的桩身加速度时程曲线按高程进行对比(图6(a)、图6(b),以峰值地面加速度(peak ground acceleration,PGA)=0.6g为例)。同时将A1,A2,A3(A1′,A2′,A3′)加速度时程峰值与A0台面峰值相比,以分析加速度放大系数沿高程的变化规律(如图7所示)。

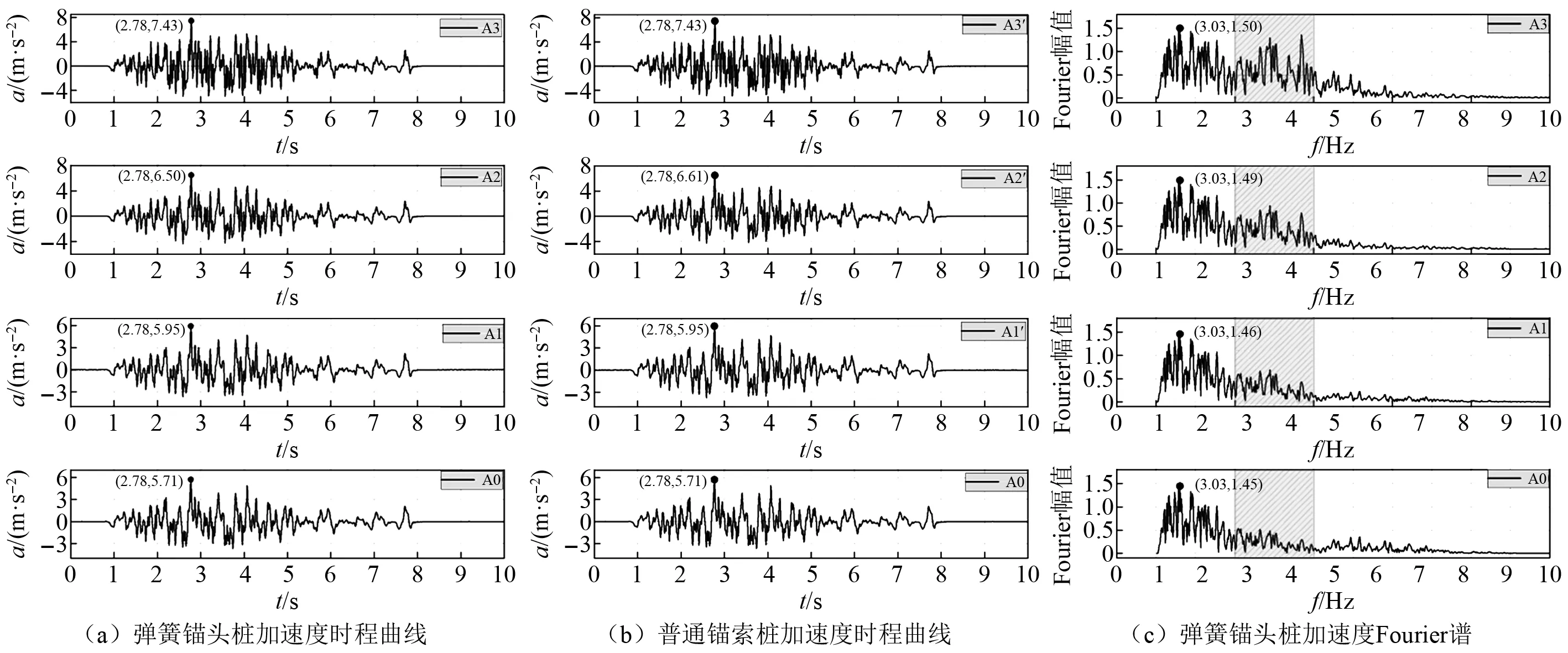
图6 加速度沿高程时频曲线(PGA=0.6g)Fig.6 Acceleration time/frequency curve along altitude

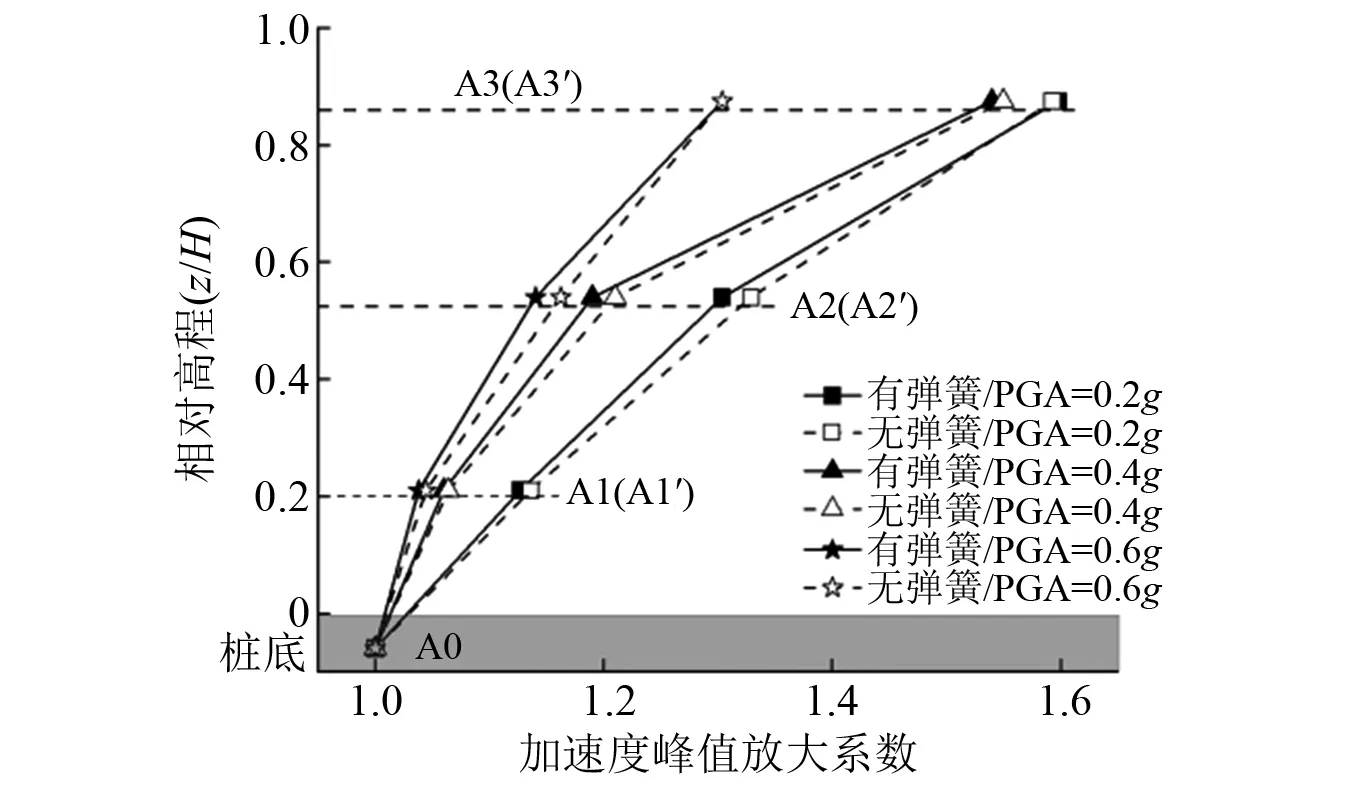
图7 桩后土体加速度放大系数随高程变化Fig.7 Acceleration amplification variation of soil behind pile along altitude

可看出,两种抗滑桩的加速度峰值放大系数均沿高程非线性增加,且随PGA增大,放大趋势减弱。设置弹簧后,桩身中部的桩后土体加速度放大系数有所减小,如当PGA=0.6g时弹簧锚头桩A2测点峰值加速度为6.50 m/s2,低于普通桩的6. 61 m/s2。在3种地震量级下,弹簧锚头桩的桩身中部加速度放大系数较普通锚索桩分别相对小3%,6%,7.5%。

考察加速度时程曲线经快速傅里叶变换(fast Fourier transform,FFT)后得到的Fourier谱,同一高程处两模型桩谱曲线基本相同,不妨以弹簧锚头桩为例进行分析,如图6(c)所示,根据频响特性将其分为低频段(0.1～10.0 Hz)、中频段(10～20 Hz)和高频段(>20 Hz)。中频段内(灰色背景区域),Fourier幅值沿高程明显增加,由台面测点的0.7增至桩顶(A3)的1.3,因此,此段为加速度高程放大的主要频段,对应原型的1.3～2.6 Hz,体现了与输入地震动主频的共振效应;低频段响应幅值较大但沿高程放大不明显,近似于刚体的传递效应;高频段不同高程加速度频响应均较弱。

2.2 桩身外倾位移响应分析

桩身外倾角θ是结构振动响应的直观表现,可通过桩顶与桩中位移数据相减并除以半桩长得到(式(1)),同理可得普通锚索桩外倾角θ′。提取两种模型桩外倾角曲线在地震过程中的正峰值及残余永久值,其随PGA的变化情况如图8所示。

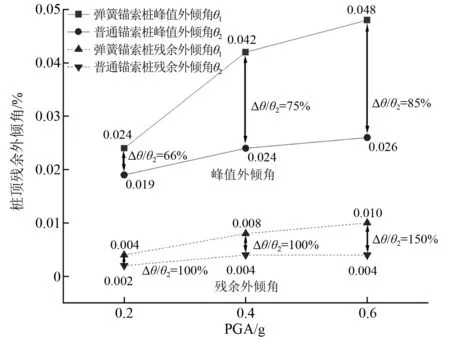
图8 桩身外倾角变化Fig.8 Variation of inclined angle

θ=2(D1-D2)/H

(1)

弹簧压缩带来的柔性效应使弹簧锚头桩较普通锚索桩的有更为显著的外倾趋势,且随PGA增长,两桩外倾角差距逐渐加大。设置弹簧后,PGA=0.2g,0.4g,0.6g时峰值外倾角较普通锚索桩分别增长Δθ/θ′1=66%,75%,85%;残余外倾角Δθ/θ′2分别为100%,100%,150%,较峰值时刻有所上涨。

3 锚索轴力时频特性与减载效应

内、外锚头为预应力锚索结构的薄弱环节,地震过程种锚索不仅会因达到受拉极限发生拉断或拔出等破坏,振动产生的多次加卸载也会引发疲劳伤损。采用时频分析研究锚索轴力时程非平稳信号,以轴力曲线正负峰值计算受力减载比与波幅减载比,通过雨流计数应力幅结合线性累积损伤理论分析锚索疲劳损伤,利用傅里叶变换得到轴力响应频率成分和频带范围,并从能量角度探寻弹簧作用频段。

3.1 锚索轴力时程特性

以设定预应力(266 N)为初始状态进行采集仪电桥平衡后加载地震波。人工波作用下弹簧锚头桩的中、边桩轴力F1,F2及普通锚索桩F′1和F′2时程曲线如图9所示,汶川波作用下中桩、边桩锚索轴力平均后的时程曲线示于图10所示。

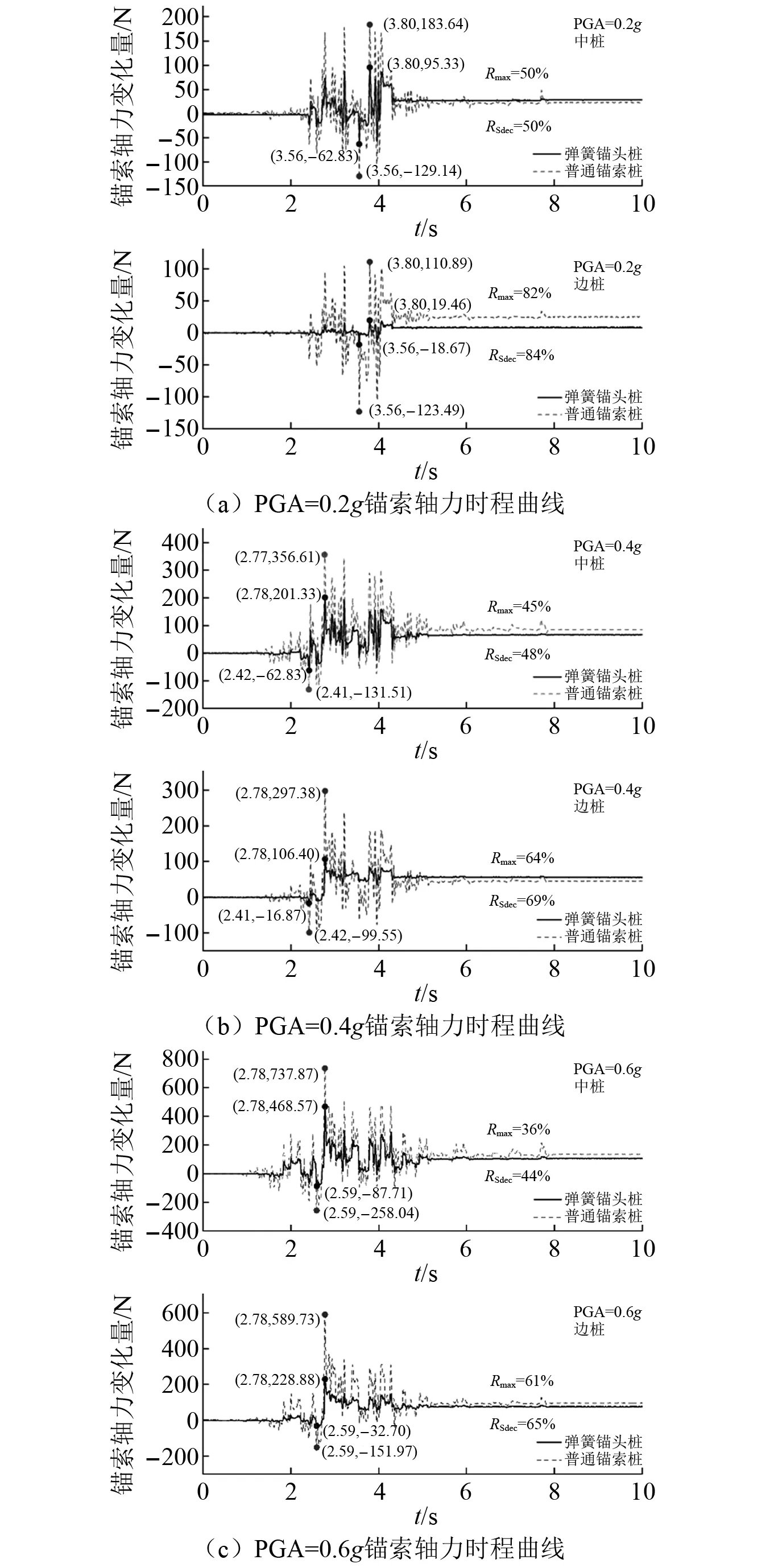
图9 人工波作用下锚索轴力时程曲线Fig.9 Axial force time-history curves under artificial wave

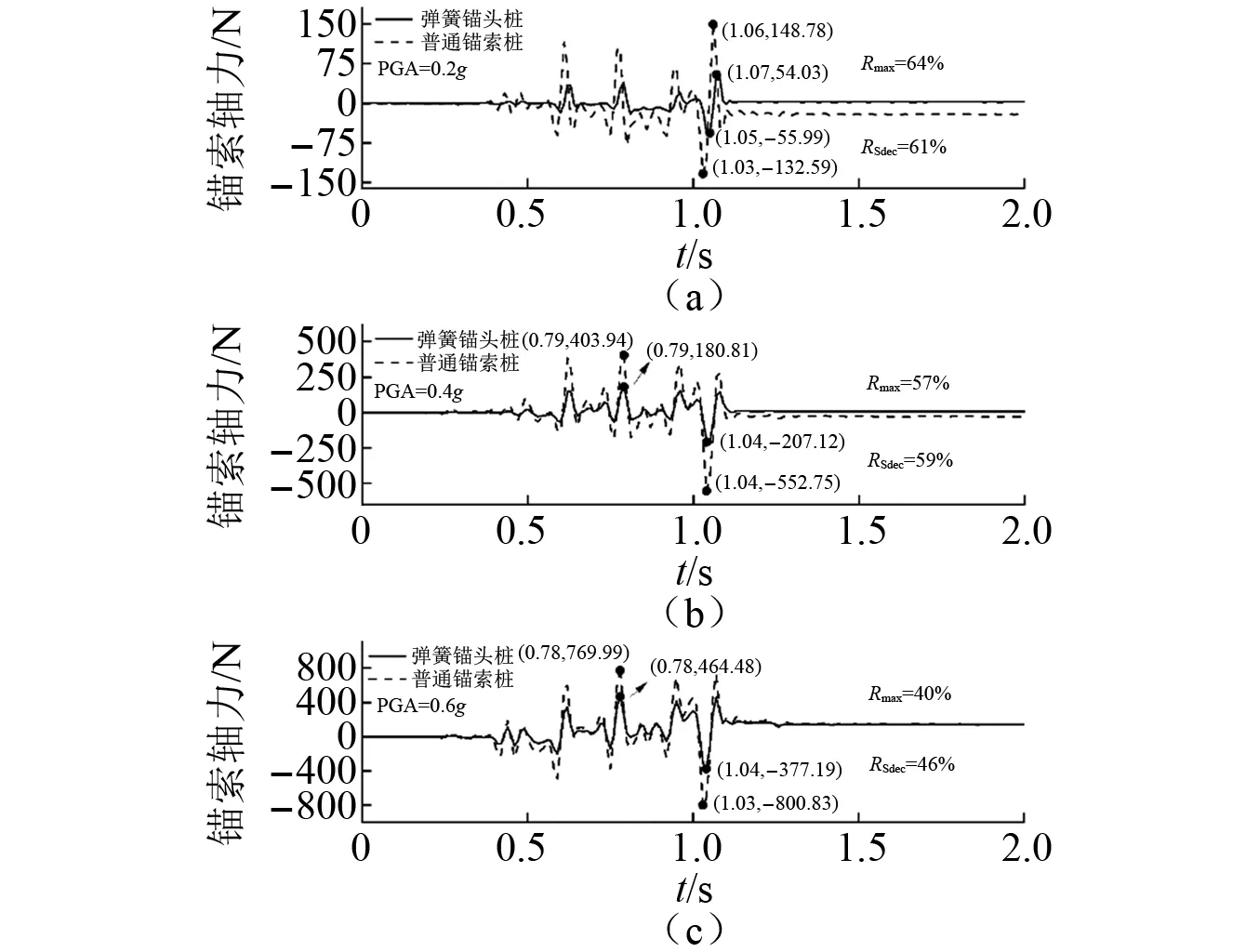
图10 汶川波作用下锚索轴力时程曲线Fig.10 Axial force time-history curves under Wenchuan Wave

3.1.1 轴力峰值

相同量级PGA作用下,两种模型桩的锚索轴力时程曲线形状相似且峰值时刻相同,且设置弹簧后轴力峰值大幅降低。为衡量峰值轴力的减载程度,定义峰值减载比如式(2)所示。

Rmax=(F′max-Fmax)/F′max

(2)

人工波作用下两模型各条件的Rmax计算结果见图9,可看出,设置弹簧后的中桩、边桩均表现出较为显著的峰值轴力减载效果,峰值减载比随PGA增大而逐渐减小。由于边界效应的影响,中桩减载程度低于边桩,中、边桩Rmax平均后与PGA呈现近似线性负相关,3种PGA下分别为65%,55%,48%。汶川波作用下的轴力峰值减载比规律性与人工波类似,Rmax分别为64%,57%,40%。两种波形的峰值轴力减载比具有一致性,最大差异不超过8%。

3.1.2 轴力波动幅值

当人工波PGA=0.2g,0.4g,0.6g时,锚索轴力最大正峰分别出现于3.80 s,2.78 s,2.78 s,最大负峰于3.56 s,2.41 s,2.59 s,最大正负峰仅间隔1～2个加卸过程,拉力在极短时间内突增,因此波动幅值过大将加剧结构脆断风险。故以波动幅值ΔSmax=Fmax+-Fmax-定义波动值减载比RSdec(见式(3))。

RSdec=(ΔS′max-ΔSmax)/ΔS′max

(3)

由RSdec计算结果(参见图9、图10)可知,弹簧锚头桩锚索轴力的波动幅值较普通锚索桩也大幅减小,随PGA增长RSdec一定程度下降。中桩减载效果弱于边桩,平均后RSdec分别为67%,58%,52%。汶川波条件的波动减载比分别为61%,59%,46%,与人工波结果较为接近,差异小于6%。

人工波和汶川波的Rmax,RSdec和前期数值模拟结果,如图11所示。两种波形作用下的减载规律具有一致性,Rmax和RSdec均随PGA呈下降趋势且数值接近,说明弹簧具有削峰和平抑波动的双重作用且效果基本等同。数值计算模型的减载比略小于振动台试验结果,反映了相似的规律性,因此综合各试验结果可得出,PGA=0.2g,0.4g,0.6g时锚索轴力减载比分别为 65%,57%,46%。

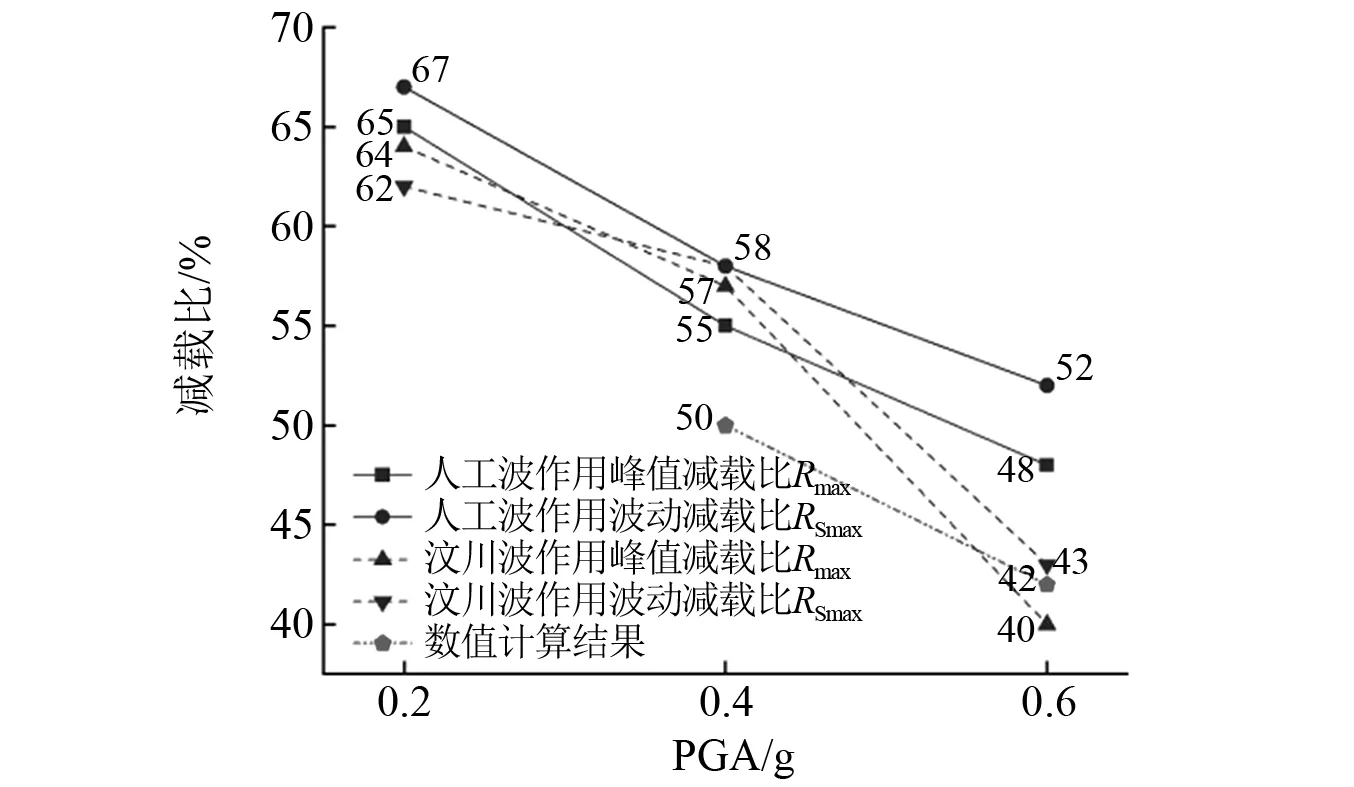
图11 峰值和波动减载比对照Fig.11 Two reduction ratios comparison

3.1.3 疲劳损伤累积效应

锚索在整个地震过程中多次受变幅荷载作用,疲劳积累导致的损伤效应是结构安全另一威胁。

Miner线性累积损伤理论[20]是疲劳分析的一种常用方法,认为同种应力幅σi产生的结构损伤与循环次数Ni成线性相关且各级损伤相互独立,总损伤D=∑Di=∑ni/Ni,D值越大则结构损伤程度越高。常利用雨流计数法[21]将复杂的应力时程曲线简化为多个幅值为σi的恒幅循环,并得到每级应力幅的出现次数ni,再根据材料疲劳特征S-N曲线计算每级σi对应的最大循环次数Ni,代入可得出D值。借鉴钢材S-N曲线方程lgNi=24.088-7.829×lgσ[22],根据锚索截面积和应力比尺将模型锚索轴力时程数据转化为原型应力数据,各工况下锚索的应力幅极值σmax和总损伤D计算结果如表3所示。

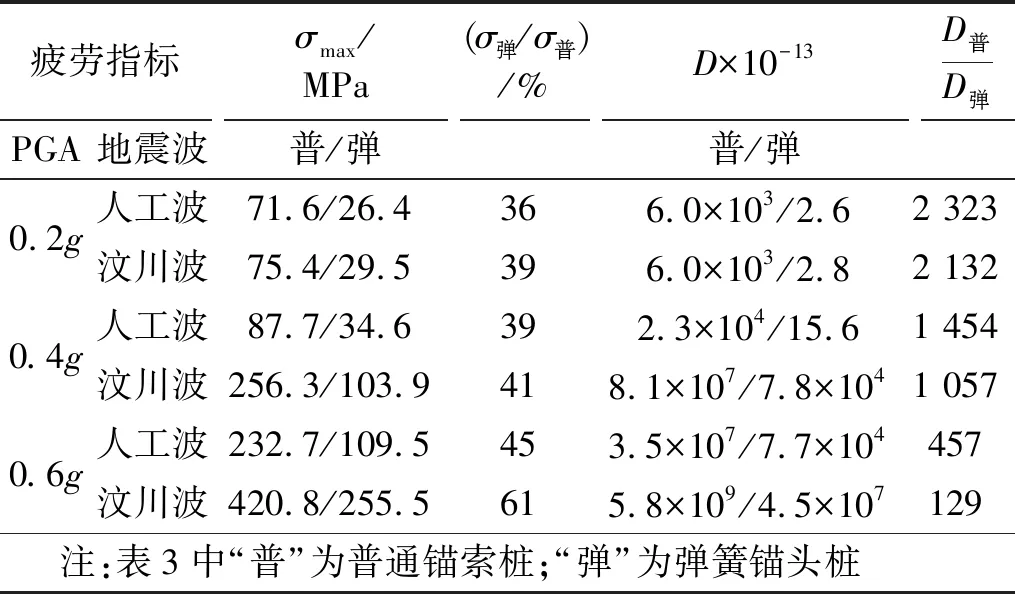
表3 锚索疲劳计算Tab.3 Anchor cable fatigue calculation

由表3可知,人工波作用下,弹簧锚头桩的锚索拉力最大应力幅小于普通锚索桩,仅为普通锚索桩的36%～45%。总损伤D因设置弹簧大幅降低,两桩损伤差异随PGA增长而减小,在PGA=0.2g,0.4g时,总损伤值下降约3个数量级,PGA=0.6g时下降两个数量级,且此时弹簧锚头桩D值仅与普通桩PGA=0.4g基本相当。汶川波作用下,弹簧锚头桩的锚索最大应力幅σmax为普通锚索桩的39%～61%,总损伤D也降低2～3个数量级。

3.2 锚索轴力频域特征

通过FFT变换将信号在时间域中的波形转变为频率域的频谱,得到3种地震量级下平均轴力Fourier幅谱如图12所示。一般情况下,可用幅度谱的平方来估计功率谱,当能量有限时,功率谱等于能量谱,因此,为探明各频段的能量响应特征,将Fourier谱幅分为Ⅰ,Ⅱ,Ⅲ区,分别对应加速度Fourier幅谱的低、中、高频段,对其幅值的平方进行频域积分,三频段的能量分布结果如图12所示,图12中Q及Q′分别为弹簧锚头桩和普通锚索桩的能量积分值,下标为积分频域段。

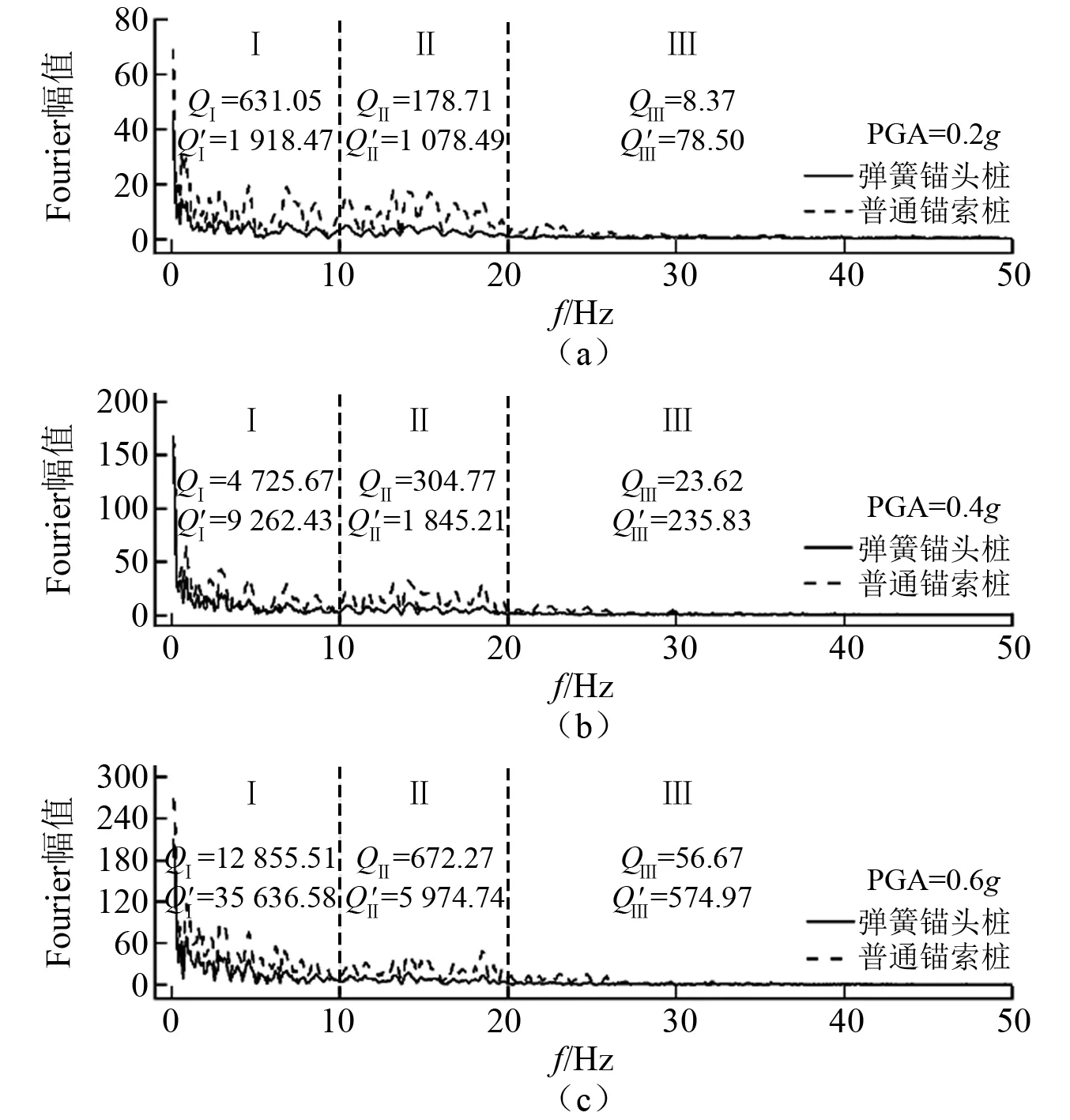
图12 人工波轴力Fourier响应幅谱Fig.12 Axial force Fourier spectrum under artificial wave

可看出:①弹簧锚头桩的锚索轴力频响在全频段均小于普通锚索桩,且中高频段尤为明显。Ⅰ区频域内,当PGA=0.2g,0.4g,0.6g时,弹簧锚头桩能量积分仅为普通锚索桩的33%,51%,36%;Ⅱ区差异增大,降为17%,17%,11%;Ⅲ区普遍小于10%。②两种桩型的锚索轴力响应能量均随频率增加而逐渐减小,反映了弹簧锚头对中高频存在过滤作用,频谱带宽由0.1～20.0 Hz减半至0.1～10.0 Hz。三量级地震强度下,弹簧锚头桩Ⅰ区能量分别占总能量的78%,93%,95%;Ⅱ区能量仅为22%,6%,5%,Ⅲ区能量小于1%,可忽略不计。而普通锚索桩在Ⅱ区仍表现较大响应能量,占总能量35%,16%,14%,较弹簧锚头桩有显著增长。

汶川波作用下的锚索轴力Fourier幅谱如图13所示。同理按能量响应特征进行频谱分区,Ⅰ区(0.1～20.0 Hz)频域内,3种PGA作用下弹簧锚头桩积分为普通锚索桩的12%,15%,38%,而Ⅱ区(20～40 Hz)能量仅9%,18%,26%。因此,弹簧锚头能显著削弱中低频、尤其中频的轴力响应,经过滤后,截止频率由40 Hz缩减至20 Hz。

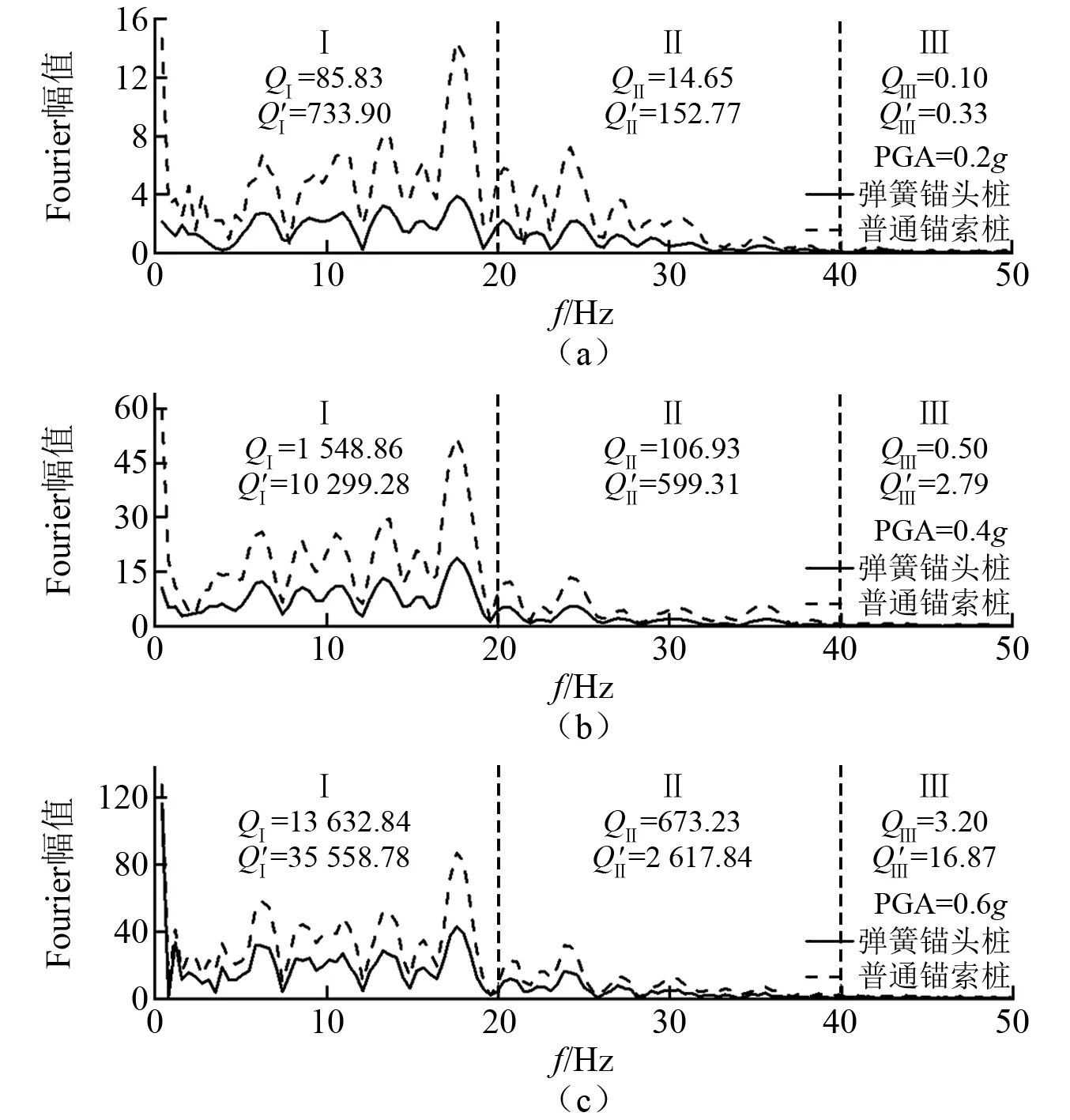
图13 汶川波轴力Fourier频谱Fig.13 Axial force Fourier spectrum under Wenchuan Wave

综上,设置缓冲弹簧不仅能削减锚索轴力幅值,缓解因拉力达到极限产生破坏,也能降低应力幅、减轻地震往复作用下的疲劳损伤。从频域角度,锚索轴力Fourier频谱均呈现“带宽减半”的频域特性,响应向低频更为集中,由于钢材的疲劳裂纹扩展速率随振动频率增加而加快[23],因此能在一定程度上降低锚固结构的中高频振动损伤风险。

锚索外锚处设置刚度合理的弹簧兼具工程可行性与明显减载效果。缩尺模型采用串联螺旋弹簧的消能部件开展试验,为增强工程实用性,应针对各个部件尤其是弹簧进行细化设计,同时考虑到弹簧刚度过柔将导致桩顶外倾变形过大,应将外倾角限值与弹簧行程一并作为弹簧刚度选取的约束条件。