倒频谱编辑法在含转子结构运行模态参数辨识中的应用

2023-10-10顾晓华张永强

振动与冲击 2023年18期

陈伟, 顾晓华, 张永强

(中国航发商用航空发动机有限责任公司,上海 200241)

振动模态参数对于结构动态特性优化有着重要且不可替代的作用。自20世纪70年代发展至今,试验模态分析成为实验室条件下静态获取结构模态参数的可靠手段。通过力锤或激振器实现人工激励,同时测量结构的响应信息,基于系统的输入和输出构造频响函数,最后使用多样的参数辨识算法进行模态参数的辨识。然而,在役结构工作环境下的边界条件有别于实验室环境,载荷条件也更加复杂。

为了解决在役结构模态参数辨识问题,工况模态分析(或称工作模态分析、环境激励下模态参数辨识)在20世纪90年代应运而生[1-2],仅基于被测结构工况环境下的响应便可辨识其模态参数。工况下结构的模态参数辨识可真实反映结构在真实边界条件下的动力学特性,且认为在结构响应中占优的频域成分即为对结构影响较大的模态。对处于复杂环境或载荷条件下的试验件,如转子叶片的“硬化”特性、流固耦合、热变形等,工况模态参数辨识算法依然适用,且能够捕捉结构在复杂环境下的真实动力学特性。此外,该测试方法依赖于环境激励或结构本身作为载荷,极大地减少了人工激励的成本,避免了对试验件的损伤[3]。

大型机械装备往往含有转子部件,如航空发动机、燃气轮机、直升机、汽车等等。转子部件在运行过程中必然带来周期性谐波激励[4]。工况模态分析的理论框架建立在宽频随机激励(或白噪声)的基础上,因此认为测量数据所识别的模态皆与被测系统的极点有关。然而,由旋转部件带来的谐波导致载荷“非白”时,依赖原有方式进行模态分析就违背了白噪声假设,使得模态参数辨识变得更加困难,导致的困难可总结为3点:首先需要从辨识的结果中区分出结构模态和“谐波模态”;其次,若输入谐波的频率接近甚至与系统的固有频率重叠时,辨识方法将无法准确识别模态参数;最后,由于强谐波载荷的存在,结构测量响应中谐波响应往往占据主导地位,导致模态参数辨识需要更高阶次的模型进行曲线拟合,辨识算法可能失去鲁棒性。

针对谐波激励下的模态参数辨识问题,学者们进行了广泛的研究,如于亮亮等[5]针对激励中含有谐波载荷时的工况模态分析,论证了人为添加谐波极点的理论可行性,并对特征系统实现(eigensystem realization algorithm,ERA)模态参数辨识算法进行了修改和验证。张义民等[6]基于随机响应与谐波信号的概率密度函数不同,区分了谐波频率,并将该方法用于国产轿车的振动模态参数辨识中。夏遵平等[7]基于谐波信号和结构模态谱峭度的不同,提出了基于谱峭度的谐波识别方法,并应用于工况下模态参数辨识。Pintelon等[8]提出了非参数模型的谐波去除方法,并将该方法应用于直升机测试数据中。类似在工程结构中的应用已有许多,如风机、汽车等,这类方法大致可归类为谐波识别类算法、谐波去除算法[9],但鲜有算法可同步实现谐波的识别与去除。

本文所提出的基于倒频谱的工况模态参数辨识方法,旨在识别含转子结构在运行状态下所受谐波激励造成的响应,以及去除谐波载荷对结构响应的影响,优化工况下振动模态参数辨识。本文首先对倒频谱的定义进行概述,并叙述了倒频谱编辑法的流程。然后,通过三自由度系统算例验证方法的可行性。接着,引入实验室条件下自由边界实心梁的试验进一步验证方法的可靠性。最后,应用于国产某型航空发动机试车数据,验证该方法的适用性。

1 倒频谱编辑法

1.1 倒频谱定义

倒频谱在齿轮和轴承的故障诊断中有着广泛的应用。倒频谱早在1963年便被引入,定义为“对数功率谱的功率谱”[10],被用于在信号中检测回声信号,该种定义的缺陷在于倒频谱不可逆。在快速傅里叶变换发展之后,倒频谱更为广泛的定义为幅值谱取对数运算后的逆傅里叶变换[11]。本文中倒频谱定义为傅里叶谱取对数运算后的逆傅里叶变换,即

Cc(τ)=F-1{In[X(f)]}=F-1{In[A(f)]+jφ(f)}(1)

式中:τ对应倒频谱的时间;X(f)为时域信号x(t)的频域形式,即

X(f)=F{x(t)}=A(f)ejφ(f)

(2)

式中:A(f)为频域幅值函数;φ(f)为频域相位函数。

式(1)所定义的倒频谱为复数形式,有幅值和相位信息。实倒频谱为幅值谱取对数运算后的逆傅里叶变换,定义为

Cr(τ)=F-1{In[A(f)]}

(3)

周期谱成分,如谐波和其倍频,在倒频谱中的表现为间距相同的峰值,因此可通过陷波器将其在倒频谱中去除。通过对实倒频谱的编辑可实现对信号幅值的调节,分离出确定性周期信号和随机信号,再结合原有频谱的相位实现不改变原信号的相位信息。

1.2 倒频谱编辑

使用陷波器对频谱进行处理时,面对多组谐波易出现处理不彻底,或误编辑的情况,从而更改了原有模态成分。将时域信号变换到倒频谱域,会使结构模态信息在信号头部集中。随着式(3)中τ的增大而使模态信号成分降低,因此本文使用前端矩形窗结合后端指数窗的形式对倒频谱进行编辑处理。修改后的倒频谱再变换到时域即实现了对谐波成分的过滤,极大地保留了信号中的模态响应成分,谐波响应对应的频谱峰值会极大降低。再通过对比处理前后的响应谱,从而实现谐波峰值的识别。因此,倒频谱编辑法可同时实现谐波响应的识别和去除,其具体步骤如下:

步骤1将时域信号进行快速傅里叶变换,得到响应的傅里叶谱。

步骤2对傅里叶频谱的幅值和相位进行分离,即分离出幅值谱和相位谱。

步骤3对幅值谱取对数,并进行逆傅里叶变换,得到实倒频谱。

步骤4对实倒频谱进行编辑,即加窗(矩形-指数窗),实现倒频谱中谐波成分的去除。

步骤5对编辑后的倒频谱进行快速傅里叶变换,得到对数幅值谱。

步骤6将处理后的幅值谱进行指数运算,并结合相位谱得到去除谐波的傅里叶谱。

步骤7对傅里叶谱进行逆傅里叶变换,获得去除谐波的时域信号,该信号可用于常规工况模态参数辨识。

具体的流程图如图1所示

图1 倒频谱编辑方法流程图Fig.1 Flow chart of the cepstrum editing method

关于实倒频谱的编辑,主要采用矩形窗结合指数窗进行。矩形窗保留了原信号中的模态成分,指数窗则消减了信号中的谐波成分,通过两者结合实现谐波的滤除。窗函数的表达式如下

(4)

式中:m为正整数,表示矩形窗的长度,因实倒频谱的不同而具体确定,文中m对应响应包络衰减90%时的信号点数;λ为正实数,表示衰减系数。

衰减系数可表达为

(5)

式中:ξ为阻尼比系数,根据谐波的强弱进行调节;fs为采样频率;fh为谐波基频的频率值。

2 三自由度系统仿真

2.1 系统特征

为了验证所提出倒频谱方法的有效性,建立一个三自由度系统,其固有频率和阻尼比如表1所示,其质量矩阵M、刚度矩阵K和阻尼矩阵C分别为

表1 构造系统的前3阶固有频率及阻尼比

在3个质量块作用了标准差为10 N满足正态分布的宽频随机噪声,在第一个自由度还作用了两组谐波:第一组基频为7.1 Hz的1倍～8倍频谐波激励,第二组的基频为16 Hz的1倍～4倍频谐波,两组谐波的幅值为1～50 N的随机整数。数据记录的采样频率为1 024 Hz,采样时间为300 s。作为例子,图2展示了第一个自由度m1测点响应的傅里叶谱。

图2 系统在谐波和随机载荷共同作用下响应谱Fig.2 Response spectrum of the system under the combination of the harmonic excitations and the random excitations

2.2 倒频谱编辑法应用

将倒频谱编辑法应用于算例中的响应信号。首先,将时域响应通过快速傅里叶变换转换到频域中,再将幅值谱取对数,并通过逆傅里叶变换得到实倒频谱,变换过程参考流程图(图 1),得到的实倒频谱见图3(a)。将长度为500的矩形窗结合指数窗的窗函数(见图3(b))施加于实倒频谱,获得修改实倒频谱,见图3(c)。最后,对修改实倒频谱进行快速傅里叶变换并进行指数运算,获得修改幅值谱,修改前后幅值谱的对比见图 3(d)。

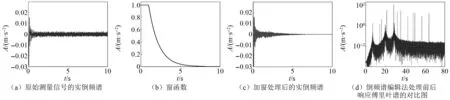
图3 倒频谱编辑法的处理过程Fig.3 Results using cepstrum editing method

由图 3(d)可知处理后的频谱中不含有谐波成分,仅含有模态峰值。因此在未知频率谐波激励下,通过该方法可识别并去除频谱中由谐波激励引起的峰值,进而确定结构固有模态导致的峰值。此外,通过谐波补偿法处理后的信号更加光滑,更易于识别频谱中的结构模态参数。

下面对处理后的响应进行工况模态辨识,使用了相关函数法[12-13](或称自然激励技术),即基于相关函数识别结构的模态参数。对去除谐波响应后的响应进行工况模态参数辨识,首先提取了响应的相关函数,通过ERA辨识算法处理相关函数,提取系统的极点,辨识的稳态图如图4所示。稳态图极点清晰,系统的前3阶模态处聚集着稳定的极点。识别的固有频率和阻尼比结果如表2所示。为了说明谐波处理算法的有效性,表 2同时展示了系统真实固有频率和阻尼比,以及直接辨识的结果,即直接对相应的相关函数使用ERA辨识算法的结果。

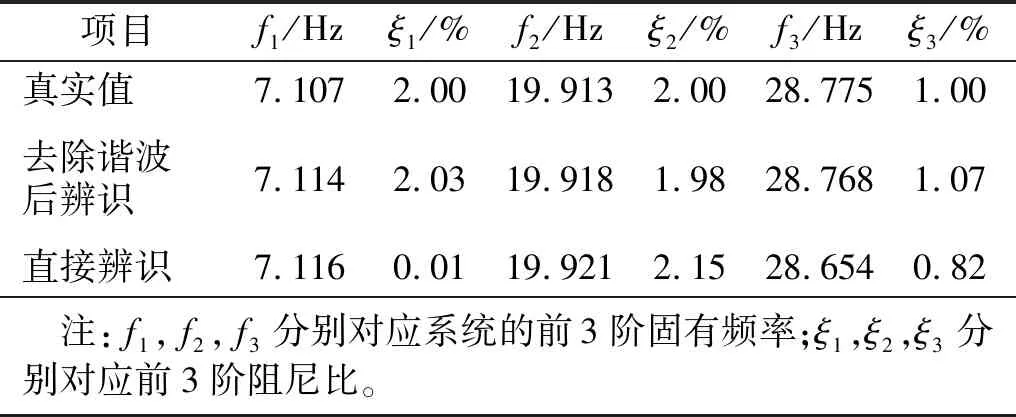
表2 识别结果的对比Tab.2 Comparison of the identified results

图4 模态参数辨识稳态图Fig.4 Stabilization diagram of the modal parameter identification

由表2结果可知,在不去除谐波影响下辨识,第一阶模态的阻尼比为0.01%,远小于结构的模态阻尼比,易造成较大误差。对于谐波与结构固有频率重叠的模态,其阻尼比识别误差较大,当使用所提方法去除谐波影响后提取的阻尼比接近真实值。

2.3 对比分析

下面进行概率密度函数法(probability density function, PDF)、谱峭度法(spectrum kurtosis,SK)、修改ERA(modified ERA, MERA)法、非参数模型法[8](non-parameter,NP)与本文所提方法倒谱编辑算法(cepstrum editing,CE)在识别谐波、去除谐波和处理谐波频率靠近模态频率情况下的对比分析。

PDF方法通过选择频谱中的峰值,以峰值频率为中心进行窄带滤波,并对滤波后的响应以幅值为横坐标以数量为纵坐标绘制直方图代替概率密度曲线。图 5(a)展示了使用PDF方法的处理结果,由于第一阶模态和第三阶模态附近存在谐波峰,PDF处理结果展示为谐波的特性,易造成结构模态的误判。

谱峭度是基于响应谱的平均计算获得,图 5(b)的虚线展示了谱峭度,图5中每个谐波峰值处对应的谱峭度值接近-1,可实现谐波的检测。但谐波靠近固有模态频率时,易发生将结构模态判断为谐波响应的情况。

图5 不同方法处理结果图Fig.5 The results of different methods

图6 测试装置布置图Fig.6 The test setup

图 5(c)展示了基于MERA方法的稳态图,相较于本文所提出处理算法的稳态图,MERA方法需要更高阶次的拟合模型获取稳定的极点,虽然谐波的模态被单独考虑,但由于谐波频率接近第一和第三阶模态且谐波幅值显著高于模态响应幅值,结构模态依然很难识别。此外,MERA方法需要在已知谐波频率的情况下进行,在谐波数量多且频率变化的情况下很难适用。

图 5(d)展示了非参数模型法的处理结果,该方法直接对响应谱进行编辑,手动去除谐波峰并进行插值。该方法在处理谐波频率靠近结构模态频率时易产生较大误差,如图 5(d)中的放大图所示,第一阶模态峰值直接被手动去除并使用线性插值补全,模态峰值处平坦,人工修改痕迹明显,相较之下本文所提的倒谱编辑法在去除谐波影响情况下保留了结构模态响应,如放大图中虚线所示。

表3总结了上述PDF、SK、MERA、NP方法和本文所提出的CE方法在检验谐波频率、去除谐波影响和处理谐波频率靠近模态频率情况的效果。根据表3,本文所提方法是对比方法中同时可以实现检测谐波和去除谐波影响的方法,且具备处理谐波频率靠近模态频率的能力,识别精度优于MERA方法。

表3 不同方法的对比Tab.3 Comparison of different methods

3 试验验证

3.1 自由梁测试

试验件为实心钢梁,其尺寸为720.0 mm×25.4 mm×25.4 mm。如图 6所示,梁的两端通过弹性绳悬挂,模拟自由边界条件。试验通过激振器模拟转子激励,激振器通过顶杆和力传感器连接在自由梁的3号位置,7个100 mV/g的微型加速度传感器均布在梁的长度方向,并通过数采系统记录梁的响应信号。

信号采样频率为6 400 Hz,每次测试记录120 s。在引入谐波载荷之前,对试验件进行传统宽频随机模态测试,获取梁的前4阶模态参数,如表4所示。随机模态测试结果将作为工况模态辨识结果的参考值。

表4 系统前4阶固有频率和阻尼比Tab.4 The first 4 natural frequencies and damping ratios

表5 稳态图中对应稳定极点开始阶次Tab.5 The start order for stable poles

在控制器端加入235 Hz, 470 Hz,620 Hz的谐波信号及信号有效值为谐波信号1/10的宽频噪声信号模拟多转子系统激励,设计的信号通过激振器作动于试验件之上。由于激振器与试验件的相互作用,结构响应谱中会出现激励谐波倍数相关的复杂谐波响应,测点1的响应时程和功率谱如图7所示。

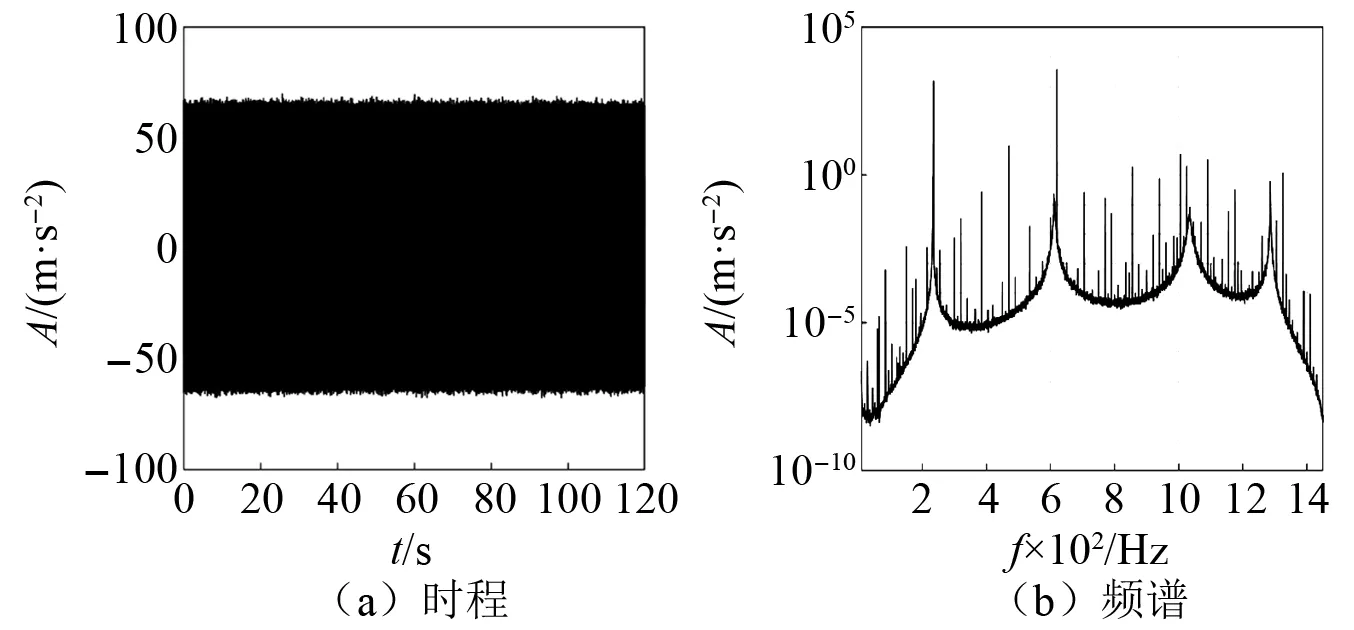
图7 测量响应信号Fig.7 The measured response from the test

下面将倒频谱编辑法应用于获取的响应信号。倒频谱编辑使用了点数为500的矩形窗结合衰减系数λ为0.2的指数窗。使用倒频谱编辑算法处理前后信号的响应谱对比见图 8,相较于原始信号(图8中实线)处理后的信号(虚线)中谐波成分有了显著下降,且模态峰值保留较好。

图8 倒频谱编辑法使用前后频谱对比图Fig.8 The comparison of the power spectrum density functions of using and without using the proposed cepstrum editing method

下面对去除谐波和未去除谐波的响应分别进行工况模态分析,使用了相关函数法进行前处理,并结合ERA辨识算法形成稳态图进行参数选取。表 5对比了去除谐波和未去除谐波获得稳定极点的ERA拟合阶次,第一阶模态进行谐波处理后,拟合阶次从39降低至6。数据显示去除谐波后获得稳定极点的拟合阶次显著下降。

以传统模态测试获取的模态参数为参考,计算谐波处理前后辨识的前4阶模态对应的固有频率和阻尼比与参考值之间的误差,结果如图9所示。未进行谐波处理时,识别的第3阶模态的频率误差为0.41%,为辨识的最大频率误差。频率误差整体相对较小,尤其体现在谐波处理后,频率辨识误差均在0.1%以内。图 9(b)中,进行谐波处理后辨识阻尼比的误差有了显著下降,第1阶模态阻尼比的相对误差从204.0%下降至12.2%,去除谐波后阻尼比的辨识相对误差均小于25%。

图9 去除谐波前后辨识固有频率和阻尼比相对误差对比Fig.9 The comparison of relative errors of identified natural frequencies and damping ratios from with processing harmonic data and without

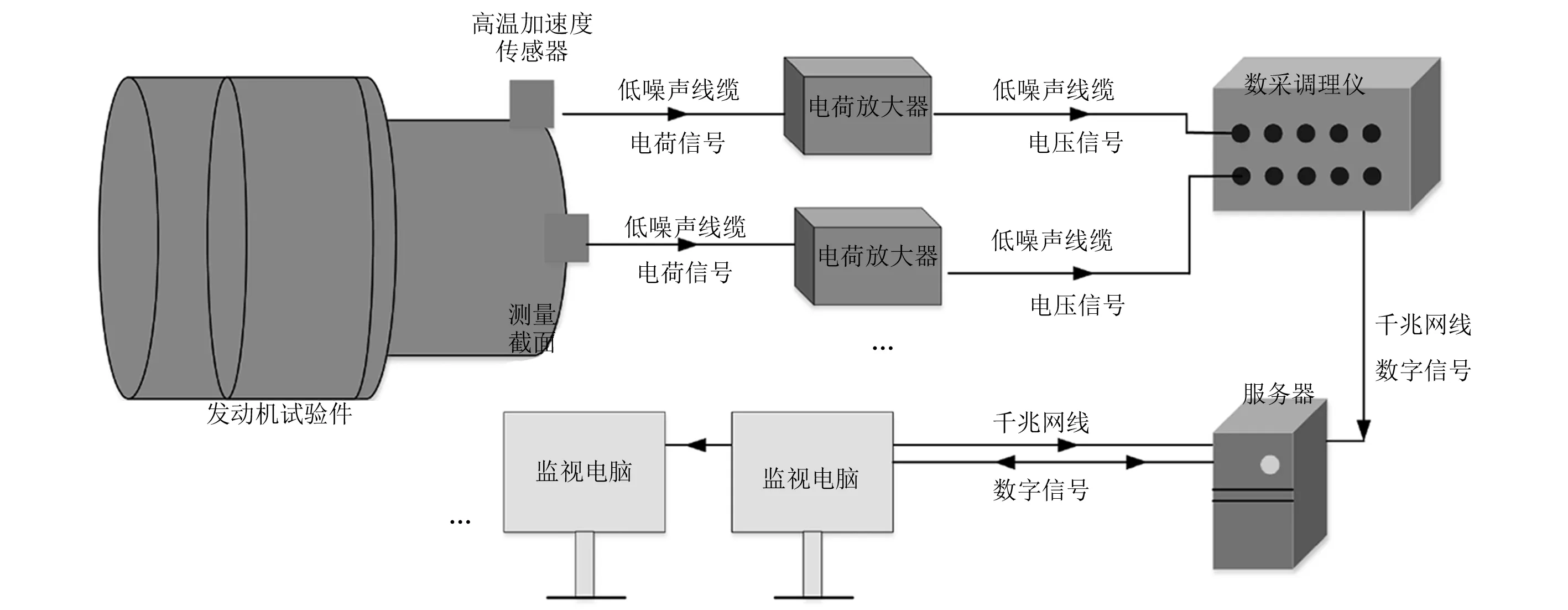
图10 测试系统布置说明Fig.10 The explanation for the experimental setup

因此,通过文中所提的倒频谱编辑算法可以有效去除谐波影响,使辨识算法的拟合阶次更低,辨识模态参数的精度更高。

3.2 发动机测试

发动机的核心机进行大气进气试验,测试布局如图 10所示,压电式高温加速度传感器布置在相应测试截面用于采集振动响应信号,并通过电荷放大器将电荷信号转换为电压信号传入数采调理仪,试验中设定采样率为25 kHz,数采调理仪实现模拟信号转换为数字信号并传输至服务器端,服务器进行数据的存储和计算,根据需要将实时处理的结果通过监视电脑展示。

分析测点位于试验件后承力机匣顺航向顺时针9点钟位置,关注频带为0～2 000 Hz,因此对获取的信号进行了重采样,处理后采样率为5 000 Hz,在试验件额定转速8 250 r/min,10 150 r/min,11 500 r/min记录了3 min数据。实测发动机试验件受到热载荷、气动载荷、转子激励等复杂激励,转速会存在一定波动,以8 250 r/min转速下测点响应的功率谱为例,具体如图11所示。由图11可知,结构所受载荷复杂,除了转子基频及分量谐波,还有多样周期性动载荷激励。

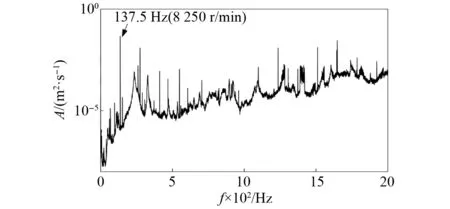
图11 响应的功率谱密度函数Fig.11 Power spectrum density function of the recorded response

将所提倒频谱编辑算法应用于测量的响应信号,处理后的实倒频谱如图12(a)所示,对实倒频谱加窗编辑,其中矩形窗的长度为10,指数窗的衰减系数λ为0.18。将编辑后的倒频谱通过图1的流程变换回时域,计算修改后信号的功率谱密度函数,修改前和修改后的功率谱对比如图12(d)所示。经过倒频谱编辑后结构模态成分被保留,而周期谐波信号被滤除,可依据处理前后功率谱中峰值的变换判断对应峰值是否由周期谐波激励导致。图12(d)中235 Hz和328 Hz对应的频谱峰未见显著变化,因此该处频谱峰为结构模态导致,进一步可基于去除谐波影响的信号进行模态参数辨识。需说明,工况模态分析仅提取试验件被激发的主要模态,235 Hz和328 Hz为发动机运行过程所激发起来静子机匣的主要模态特征,被激发的模态与机匣本身结构和运行环境有关。

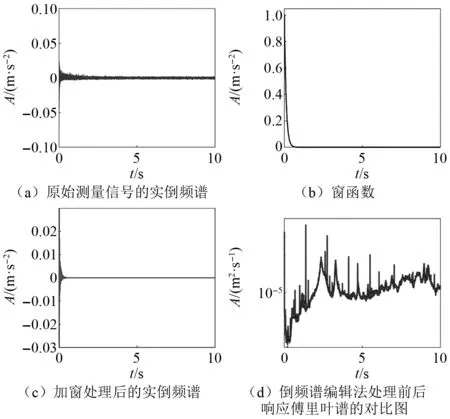
图12 谐波去除过程图Fig.12 Process of harmonic response removal

对去除谐波后的时域响应进行基于相关函数的工况模态分析,即对响应信号做相关运算后,再使用ERA算法结合稳态图进行模态参数辨识。辨识稳态图如图13所示,辨识的模态参数结果如表6所示。图 13中235 Hz和328 Hz峰值处系统辨识结果清晰稳定,去除谐波影响后模态参数辨识更为简单。

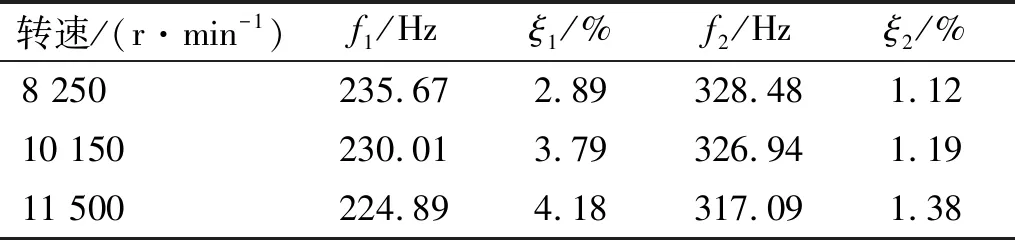
表6 核心机在不同转速下机匣模态参数辨识结果

图13 模态参数辨识稳态图Fig.13 Stabilization diagram of the modal parameter identification

通过对比去除谐波成分前后响应谱,可判断频谱中对应结构模态的峰值,获得了清晰的稳态图,从工况试车数据中识别了结构的振动固有频率及阻尼比参数。由于发动机结构动力学特性受到其运行状态影响(温度、压力等变化),在不同转速下其固有频率和阻尼比也发生不同程度变化,在10 150 r/min和11 500 r/min转速下识别的模态参数见表6,随着转速的升高,结构固有频率有着较为显著的下降趋势。综上,所提方法可在发动机运行工况下识别其固有频率和阻尼比,可在实际环境下识别发动机机匣的动力学特性,有利于追踪其动力学特性随试验条件的变化。