同轴离心式喷嘴燃烧稳定性增长率识别
2023-10-10杨尚荣吴林龙杨宝娥
杨尚荣, 吴林龙, 于 涵, 杨宝娥
(西安航天动力研究所 液体火箭发动机技术重点实验室, 西安 710100)
燃烧不稳定是航空航天发动机研制中需要重点关注的问题,通常表现为燃烧室声模态频率附近的高幅值压力振荡。国内外在其产生机理、评估和预测方法、以及控制手段等方面开展了大量的研究[1-2]。目前预测方法在工程上的应用还未成熟,尚不能在发动机试验前对其稳定性进行可靠的预测。因此一旦出现燃烧不稳定,通常从两方面出发去解决:一方面减少激励能量;另一方面增加燃烧室声学阻尼。前者需要考虑燃烧和声场间的耦合作用过程,由于燃烧现象本身的复杂性,实施改进方案难度较大。相比较而言,被动阻尼装置的设计要容易一些。
从线性角度,增长率表征小扰动下燃烧室振荡能量的变化率。如果其值大于零,说明系统不稳定,反之,说明系统稳定,此时增长率也称为衰减率。对于出现燃烧不稳定的燃烧室,新设计阻尼装置的衰减率应大于燃烧室的增长率并保留一定的裕度,即需要燃烧室不稳定声模态的增长率作为设计输入参数。
学者们提出了多种方法来识别增长率。主要分为外部激励方法(输入-输出识别)和无外部激励方法(仅输出识别)。外部激励方法中,对于Hopf类型的分叉,Lee等[3]利用分叉前的噪声相干共振特性[4],识别系统的非线性燃烧响应,外推出系统分叉点的位置和类型、增长率、极限环振荡幅值等,进一步可以对系统稳定性边界进行预测[5]。另一类方法采用主动控制[6],在不稳定工况点施加和关闭控制,获得振荡幅值从小扰动增加到极限环的过程。利用振荡幅值初始增长阶段(满足线性假设)数据,拟合指数函数或采用其他数据处理方法(如DMD(dynamic mode decomposition)[7])识别增长率。实际发动机试验中加入特定形式的外部激励或主动控制比较困难,因此外部激励方法在工程应用中不方便。
无外部激励的方法,第一类与主动控制方法中关闭控制后的处理方法相同,区别是利用自发燃烧不稳定振荡幅值初始增长阶段数据[8]。另一类方法基于噪声激励作用下燃烧室声模态的随机动力学理论[9],从极限环振荡数据中提取线性增长率。根据噪声强度等级,Noiray等[10]提出对应的3种识别方法,并利用燃气轮机中压力振荡数据进行了比较。进一步,利用数值模拟[11]和燃烧器试验[12]对第三种方法进行了验证。Bonciolini等[13]比较了彩色噪声和白噪声的激励效果,发现在振荡频率附近采用合适的带通滤波,两者的区别可以忽略。若带通滤波过窄,则两者的识别结果差别较大。Boujo等[14]通过引入伴随优化方法解决了上述问题。即使考虑燃烧响应相对于压力振荡的时间延迟,该方法依然可以较准确的识别线性增长率[15]。Hummel等[16]将方法推广到周向不稳定对声模态增长率的识别。
本文开展同轴离心式喷嘴稳定性试验研究,采用无外部激励方法识别不同工况下的线性增长率,并对其参数敏感性开展分析,为液体火箭发动机燃烧稳定性分析提供参考。
1 试验工况和分析方法
1.1 试验工况
燃烧试验系统的详细介绍参见文献[17]。模拟燃烧室为敞口圆筒形结构。试验用喷嘴(如图1所示)为带缩进室的同轴离心喷嘴,外喷嘴为煤油离心喷嘴,内喷嘴为直流氧化剂喷嘴。
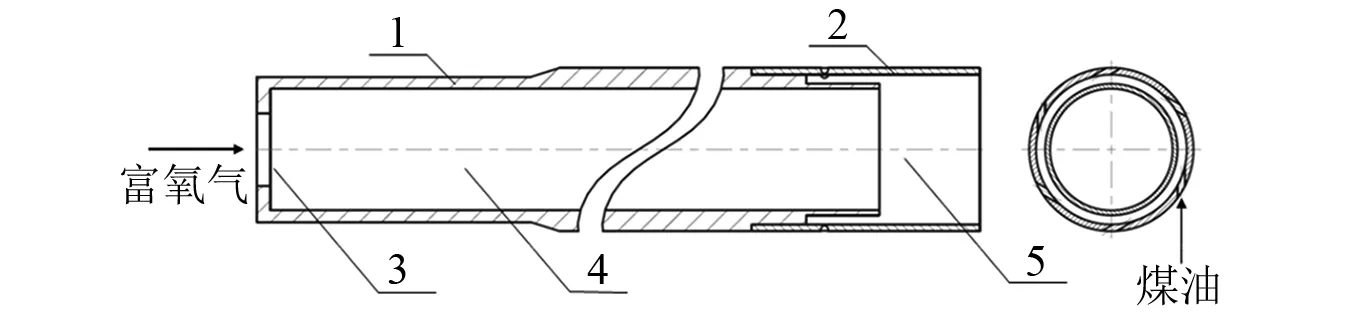
1. 直流喷嘴; 2. 离心喷嘴; 3. 节流嘴; 4. 富氧气通道; 5. 缩进室。图1 带缩进室的同轴离心喷嘴Fig.1 Recessed swirl coaxial injector

表1 试验工况Tab.1 Test operating conditions
1.2 数据分析方法
当燃烧室只有单阶声模态振荡时,可以不考虑模态间的耦合作用。压力振荡可以用非线性振动方程描述
式中:η为脉动压力;f为由气动力和燃烧过程产生的激励源项;α为声模态衰减率;ω0为声模态角频率;ξ为燃烧噪声,假定为高斯白噪声,有〈ξξτ〉=Γδ(τ),Γ为噪声强度。
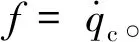
(2)
假定压力振荡接近谐振,可以将脉动压力写成如下幅频形式
η(t)=A(t)cos[ωt+σ(t)]
(3)
式中,A(t)和σ(t)分别为压力振荡的幅值和相位。代入式(2),利用随机平均方法,式(2)可以写成幅值A和相位σ的一阶随机微分方程。由于A和σ可以解耦,仅列出幅值A满足的方程
(4)
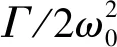
(5)
驻定情况下,FP方程存在解析解
(6)
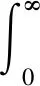
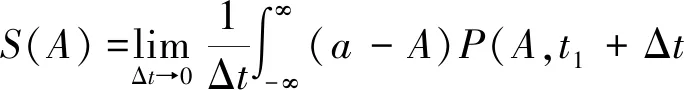
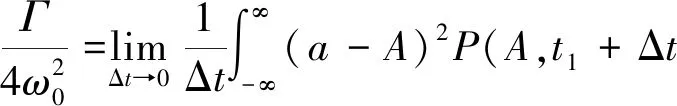
(7)
进一步通过非线性拟合识别出线性增长率ν、饱和系数κ和噪声强度Γ。
2 试验结果及分析
2.1 压力时间序列
不同混合比条件下的压力时间序列及其对应的相空间轨迹如图2所示。当混合比为15.0时,压力振荡幅值较小,认为是燃烧噪声阶段,相轨迹图为无序轨迹线的聚集。当混合比为17.5时,振荡幅值增加,振幅波动也较大,轨迹在不同幅值周期振荡之间转变,中心为空心。当混合比为20.0和22.5时,达到极限环振荡,轨迹图为圆环面,环的宽带代表噪声对幅值的影响。时频分析显示振荡燃烧频率在(2 340±100)Hz内。
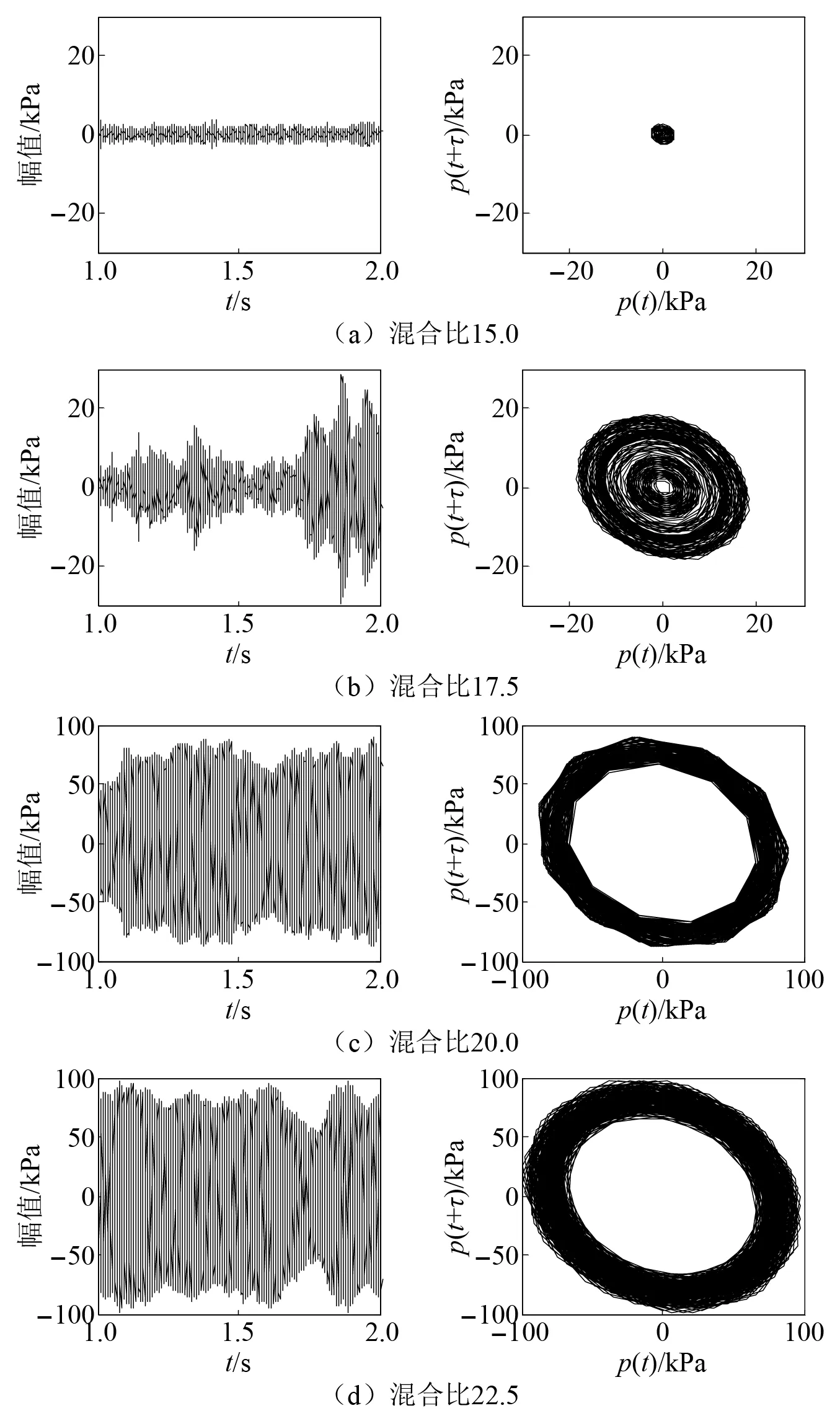
图2 压力时间序列和相空间轨迹图Fig.2 Pressure time series and phase portrait
2.2 数据单位的影响
试验中压力数据有单位,如Pa,kPa等。本节分析压力数据取不同单位时对识别结果的影响。令幅值A(t)=kB(t),k为单位间的换算关系,B(t)为换算后的幅值时间序列。代入式(5),化简并结合可得
(8)
比较式(5)和式(8),可知单位变换后,增长率不变,饱和系数为原来的k2倍,噪声强度为原来的1/k2倍。
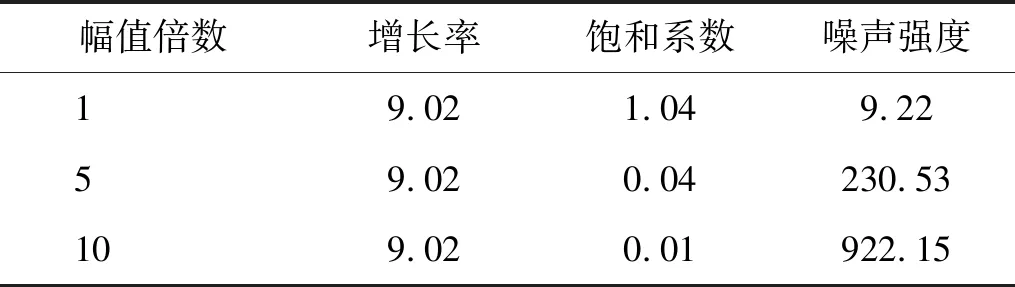
表2 不同幅值下参数识别结果
2.3 试验数据增长率识别
本文压力单位选用kPa进行数据分析,其他单位下的饱和系数和噪声强度可通过2.2节换算关系得到。4种工况下压力时间序列识别结果如图3所示。随着混合比增加(总流量也增加),压力振荡均方根(root mean square,RMS)幅值增加,增长率ν由负值转变为正值,饱和系数κ下降,噪声强度Γ增加。具体地,当混合比为15.0时,其增长率为负值,系统是稳定的。当混合比为17.5时,增长率也为负值,从线性角度分析系统应该是稳定的。但从图2压力曲线和相轨迹可知,其周期性振荡幅值也较大。说明存在噪声条件下(实际发动机中燃烧噪声不可避免),不仅要保证系统增长率为负,还需要留有一定裕度,才能保证系统不发生大幅值周期振荡。当混合比为20.0和22.5时,增长率均为正值,且幅值越高,增长率越大。该结果不能作为通用结论来推广,理论上,以式(2)作为控制方程的系统,压力振荡幅值由增长率ν和饱和系数κ共同决定。不同工况下,饱和系数κ非定值。此外试验中也发现较高幅值的压力振荡并非一定对应较大的增长率[20]。
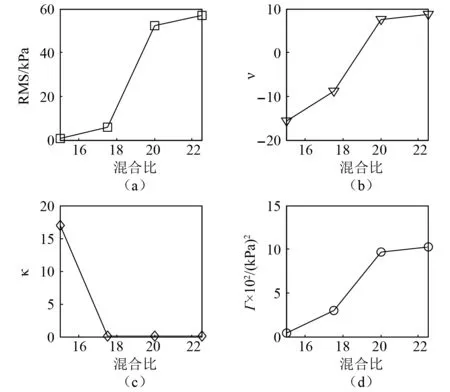
图3 试验压力时间序列RMS值和识别结果Fig.3 RMS values of test pressure time series and identification results
将识别结果代入FP方程解析解式(6),与试验压力振荡幅值概率密度分布进行比较,如图4所示。当混合比为20时,试验结果和识别结果差别较大,其他工况结果相对较好,一定程度上验证了燃烧响应模型和识别方法的合理性。Oriray研究中的数值试验发现增长率在-5~5 rad/s内时,准确识别需要约30 s时长的数据。本文试验采样时间T=5 s,相比准确识别所需的数据长度而言较短,因此需要对识别结果的不确定性进行分析。
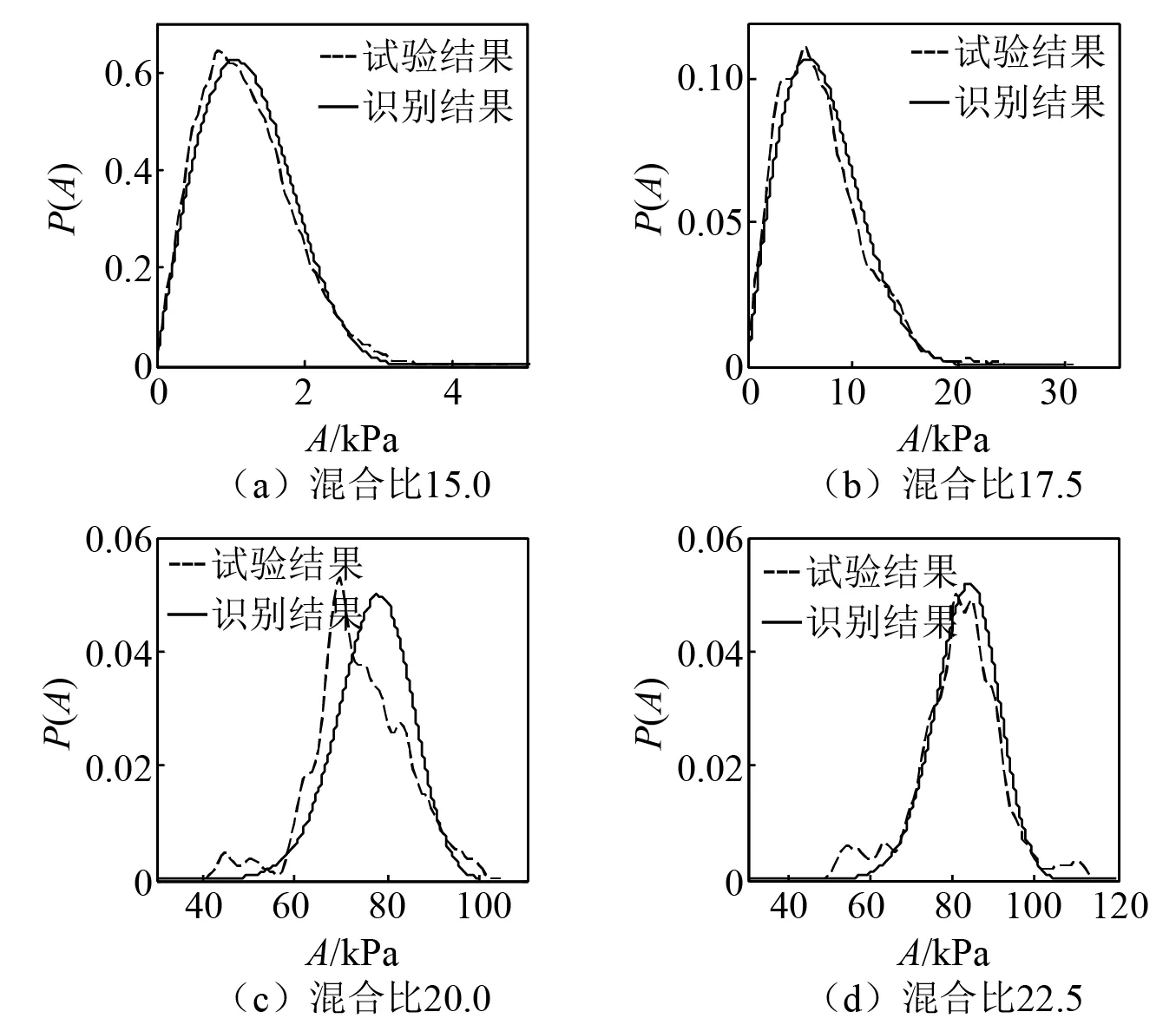
图4 振荡幅值概率密度函数Fig.4 Probability density function of oscillation amplitude
2.4 敏感性分析
本节分析识别结果的不确定性以及数据采样时间和采样频率对识别结果的影响。每个工况下试验数据只有一次,且系统真实的增长率未知。因此,为了量化识别方法的不确定性,将每个工况下的识别值作为设定值,数值求解随机微分式(2)生成100组压力时间序列,识别其增长率并取平均值和标准差,来量化该工况下识别结果的不确定性。
4个工况下的计算结果如图5所示。采样时间T和采样率sf与试验中取值相同,即T=5 s,sf=25.6 kHz。结果表明,当混合比为20.0和22.5时,增长率均值与设定值偏差分别为11%和15%,标准差分别为17%和20%。当混合比为15.0和17.5时,增长率均值与设定值偏差分别为76%和50%,标准差分别为62%和56%。工程应用时可以确定一个阈值,设定值(试验数据识别值)与识别值偏差小于该阀值时,则可以将识别值的标准差作为设定值的标准差,从而确定识别结果的不确定性。
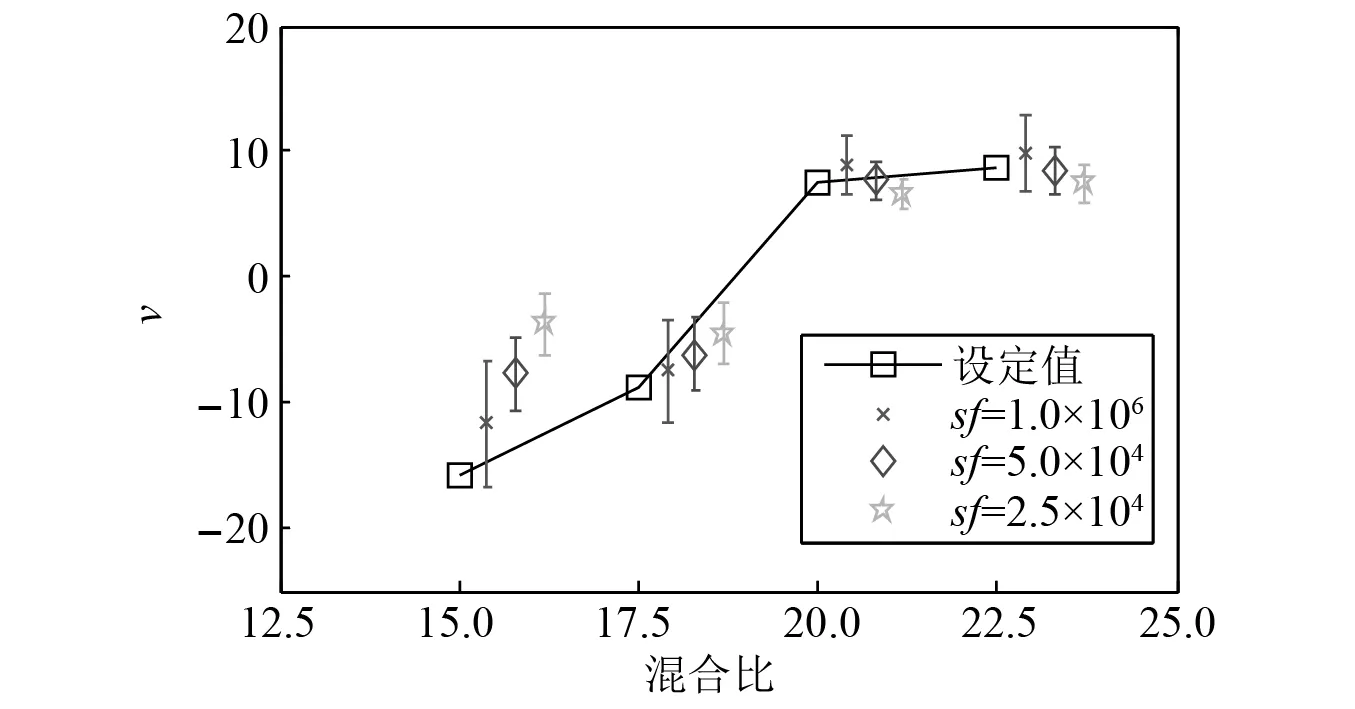
图5 采样率对增长率识别的影响,采样时间T=5 sFig.5 Effect of sampling rate on growth rate identification, sampling time T=5 s
采样频率对结果的影响见图5,采样时间均为5 s,采样率分别为25.6 kHz,50 kHz,1 000 kHz。均值和标准差均由式(2)生成的100组压力时间序列计算得到。对识别值的横坐标作了平移,以便图形能清晰表达。增加采样率,当混合比为15.0和17.5的偏差(设定值与识别均值之差)减小,混合比20.0和22.5的偏差在采样率50 kHz时最小,4个混合比下其识别值的标准差均增加。
采样时间对结果的影响如图6所示,采样频率均为1 000 kHz,采样时间分别为1 s,3 s,5 s。每个均值和标准差均由式(2)生成的100组压力时间序列计算得到。同样对识别值的横坐标作了平移。从图6可知,增加采样时间,4个混合比下识别值的偏差和标准差均减小。由此可知,为了增加识别的精度,应该增加采样时间,同时提高采样频率,以便在数据分析时可选出对应工况下较优的采样频率。
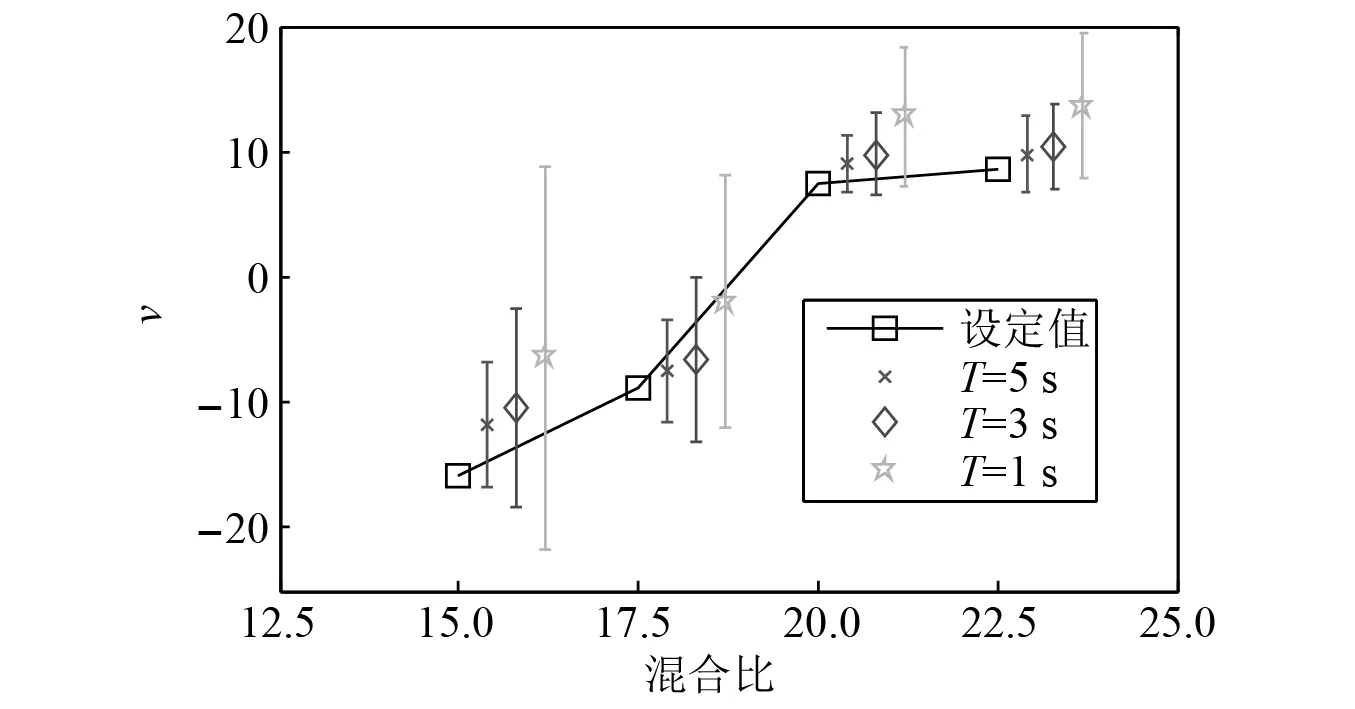
图6 采样时间对增长率识别的影响,采样率sf=1 000 kHzFig.6 Effect of sampling time on growth rate identification, sampling rate sf=1 000 kHz
3 线性增长阶段增长率识别
增长率也可以从压力振荡幅值线性增长阶段识别得到。由于压力振荡幅值在线性增长阶段以指数形式增长[21],因此可对压力振荡时间序列取包络,利用指数函数去拟合,或将包络取对数后利用线性函数去拟合。本章分析噪声对增长率识别结果的影响。
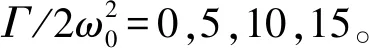
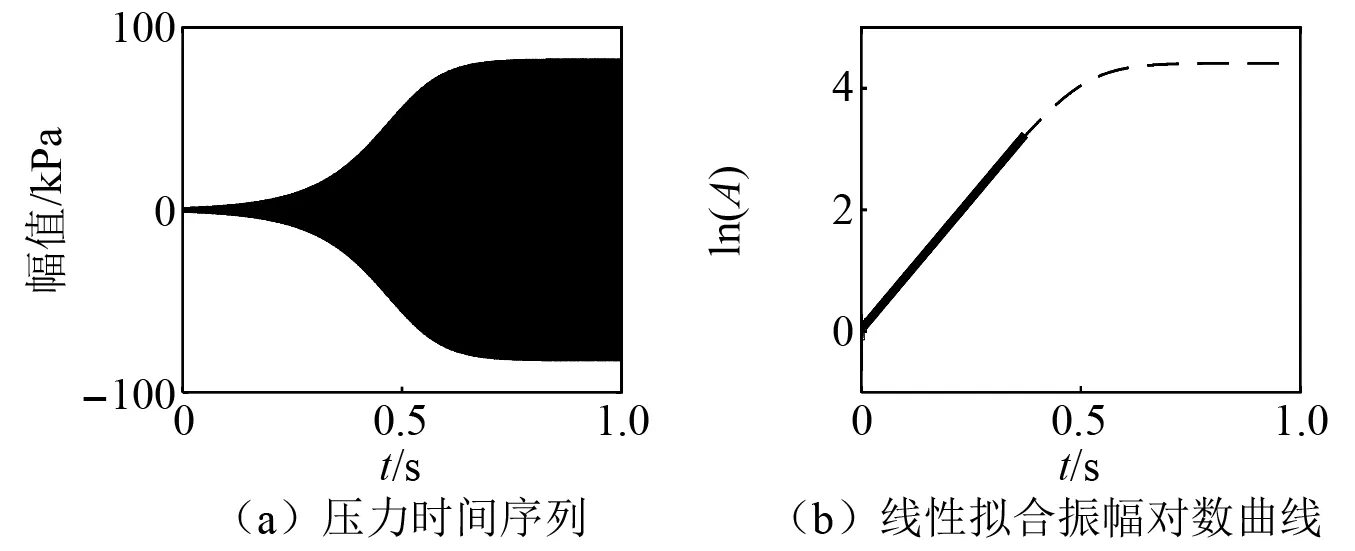
图7 无噪声压力时间序列和增长率识别Fig.7 Noise free pressure time series and growth rate identification
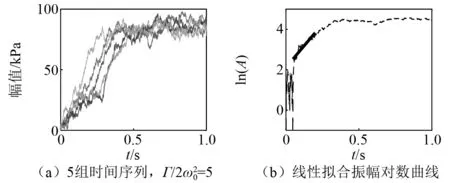
图8 含噪声压力时间序列和增长率识别Fig.8 Pressure time series with noise and growth rate identification
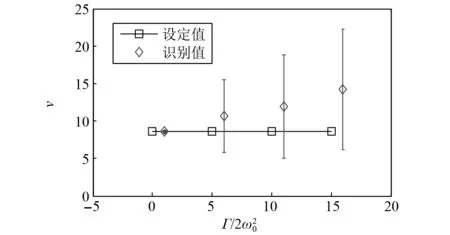
图9 噪声对增长率识别的影响Fig.9 Effect of noise on growth rate identification
4 结 论
(1)压力振荡幅值的单位不改变增长率的值,但会影响饱和系数和噪声强度,理论上得到了相似关系并获得了数值试验的验证。
(2)即使增长率小于零,如果噪声强度较大,系统也有可能发生较大幅值的压力振荡,因此系统增长率应该留有一定裕度。
(3)提高采样时间可以提高识别精度,不同工况下存在各自较优的采样率。
(4)当噪声强度较大时,从振幅线性增长阶段识别增长率存在较大误差,需要考虑噪声导致的不确定性。
