基于云模型和离散卡尔曼滤波的临时看台结构动荷载识别

陈文博, 郭惠勇

(1. 重庆大学 土木工程学院,重庆 400045; 2. 四川电力设计咨询有限责任公司,成都 610016)

临时看台结构由于其施工灵活性高、周期短、可回收循环利用等优点,被广泛应用于各种大型文体活动中。当看台结构上人群拥挤、摇摆以及跳跃时,其容易发生较强振动导致看台倒塌等事故的发生[1]。例如1994年,伦敦的一场音乐会上,由于观众随着音乐摇摆、跳跃,导致看台发生倒塌,超过50人受伤。2010年9月,在巴西举办的一场赛车比赛中,超过500名观众到场观战。由于观众有节奏摇摆、跳跃,临时看台结构发生倒塌,现场百余人受伤;2012年2月,王菲重庆演唱会中,当王菲入场时,大部分观众整体起立欢呼雀跃,观众席随之发生倒塌事故,造成60余人受伤,演唱会临时取消;2021年3月22日,在印度第47届全国青年锦标赛开幕仪式上,临时看台突然倒塌,超过100名观众受伤。2021年5月,在以色列的一座犹太教堂,由于看台上观众过多导致临时看台坍塌,造成200余人受伤,数人死亡。可以看出,人群荷载的作用,包括人群的拥挤和跳跃、摇摆等产生的动荷载常常是看台等临时设施结构安全的重要影响因素[2]。而国内外学者对看台等临时结构荷载识别工作研究较少,因此有必要对此类结构进行人群等荷载的快速识别研究。

当前针对临时看台结构的研究主要集中于看台结构优化设计[3]、安全评价[4]、看台承载能力[5]、节点刚度[6]、风荷载分析[7]等方面,而对看台结构荷载识别方法的研究相对较少。其中,Celik等[8]提出了一种计算机视觉方法,用于测量由于个人和人群跳跃和摆动引起的荷载时程。该方法包括使用基于光流算法跟踪个人和人群的位移轨迹以及实验室内的测力板测试单人和人群跳跃摇摆产生的荷载,并通过现场演示进一步验证。因此,本文针对某比赛实际看台的等效简化模型进行了荷载识别研究。首先描述了云模型和离散卡尔曼滤波的基本原理。随后,基于离散卡尔曼滤波推导出动荷载识别算法,并利用云模型技术进行优化得到基于云模型和卡尔曼滤波的动荷载识别方法。其中云模型技术有效解决了测量误差、环境噪声等带来的干扰问题。最后,将该方法应用于临时看台结构的数值仿真,验证该方法对临时看台结构动荷载识别的有效性。

1 云模型和离散卡尔曼滤波基本原理

1.1 云模型和数字特征

1995年,中国工程院院士李德毅结合模糊数学和概率论的相关知识提出云模型的概念,主要用于定量数值与定性概念之间的互相转换,可有效解决定性和定量相结合的不确定性问题[9]。

云的数字特征主要包括期望Ex、熵En和超熵He,云的3个数字特征可以描述云模型的整体特征,从而实现定性和定量之间的相互转化。3个数字特征的定义如下[10]。

期望Ex:期望值是云的中心位置反映在云图横坐标上的值,表示该点为论域中最能够表示定性概念的点。

熵En:熵最早是一个热力学概念,本质是一个系统的“无秩序程度”。在云模型中,熵用来表示定性概念的不确定性的度量:一方面,它反映了定性概念模糊性的裕度;另一方面,通过云滴的分布位置的稀疏和稠密反映了定性概念在此空间中出现的概率,即为该定性概念的随机性。

超熵He:超熵可以理解为熵的熵,体现了云滴之间的离散程度,用来度量熵的不确定性。

1.2 离散卡尔曼滤波

理论上,所有基本物理时间均在连续时间内发生,但在实际研究工作中,为了方便计算机的求解,需要将连续时间系统进行离散化,即在计算机的数值计算研究中,采用的是时间离散型卡尔曼滤波器。离散卡尔曼滤波器不需要计算机存储大量数据,并且在输入新的观测数据后,可以迅速得出新的状态估计值,具有很高的时效性且容易实现[11]。

离散系统主要用以下两个基本方程来描述。

系统状态方程

X(k)=ΦX(k-1)+Bω(k-1)

(1)

系统观测方程

Z(k)=HX(k)+υ(k)

(2)

式中:X(k)为kΔt时刻的系统状态向量;k为采样时刻;Δt为数据的采样时间间隔;Φ为状态转移矩阵;H为观测矩阵;B为驱动矩阵;ω(k)和υ(k)分别为系统噪声和测量噪声,代表系统建模的误差和传感器测量的误差。

噪声特性假设如下。

(1)ω(k)和υ(k)均为高斯白噪声时间序列,即

E[ω(k)]=0

(3)

E[ω(k)ωT(l)]=Q(k)δkl

(4)

E[υ(k)]=0

(5)

E[υ(k)υT(l)]=R(k)δkl

(6)

式中:Q(k)和R(k)为协方差矩阵;δkl为kronecker-δ函数,其定义如下

(7)

(2)ω(k)和υ(k)互不相关,即

E[ω(k)υT(k)]=0

(8)

(3)ω(k)和υ(k)都与初始状态X(0)不相关,即

(9)

离散卡尔曼滤波器的工作原理[12-13]为:首先采用前一时刻的状态估计值递推计算当前时刻的状态估计值,然后通过反馈当前响应的实际测量值的方法来修正当前的状态估计值,实质上是一个不断重复“预测-实测-修正”的顺序递推。算法流程分为时间更新和测量更新。其中,时间更新起到预测作用,包括当前时刻的状态矩阵和协方差矩阵的估计,主要依靠系统状态方程和噪声参数,目的是为下一时刻的状态估计提供先验估计;测量更新在时间更新的基础上,利用响应的实际测量值与当前时刻的状态值之间的线性关系,负责反馈并校正当前估计值,同时也为下一时刻提供修正后的后验估计。

离散卡尔曼滤波器具体公式如下所示。

时间更新

(10)

P(k/k-1)=ΦP(k-1/k-1)ΦT+BQBT

(11)

测量更新

J(k)=HP(k/k-1)HT+R

(12)

Ka(k)=P(k/k-1)HTJ-1(k)

(13)

P(k/k)=[I-Ka(k)H]P(k/k-1)

(14)

(15)

(16)

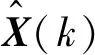
2 基于云模型和离散卡尔曼滤波的结构动荷载识别方法

2.1 基于离散卡尔曼滤波的动荷载识别方法

基于离散卡尔曼滤波的基本原理,本节从离散系统的角度研究动荷载反演。

对于一个有n个自由度的线性结构,其动态系统的运动方程为

(17)

式中:M,K,C分别为质量矩阵、刚度矩阵、阻尼矩阵;Y(t)为位移响应;F(t)为荷载列阵。将上述运动方程转化为状态方程,可以写为如下形式

(18)

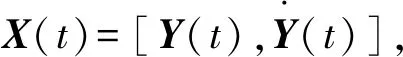
(19)

将状态空间状态方程转化为模态空间状态方程可得

(20)

(21)

(22)

(23)

式中:Φi,fi,Ci,Ki,ξi,ωi分别为按质量规准化的第i阶振型、模态荷载、阻尼、刚度、阻尼比、自振频率。

式(20)为矩阵形式的微分方程,其解析解为

Xi(tk+1)=Φi(k+1/k)Xi(tk)+Гi(k+1/k)fi(tk)

(24)

Φi(k+1/k)=exp[AiΔt]

(25)

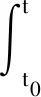
(26)

式中:Г为驱动矩阵,当Δt取值一定时,Φi(k+1/k)和Гi(k+1/k)均为常量矩阵,所以式(24)可简写为

Xi(tk+1)=ΦiXi(tk)+Гifi(tk)

(27)

以结构的位移、速度或加速度响应为观测值,观测方程为如下形式

Zi(t)=HiXi(t)+Difi+εi

(28)

式中:Zi(t)为观测值;Hi为观测矩阵;Di为系统矩阵;εi为观测噪声。

当观测响应为位移时

Hi=[10],Di=0

(29)

当观测响应为速度时

Hi=[01],Di=0

(30)

当观测响应为加速度时

Hi=[-Ki-Ci],Di=1

(31)

对比式(28)和离散卡尔曼滤波基本方程可得:观测方程中多出一个未知输入项Difi,不符合滤波基本方程的构造形式,无法直接对系统状态响应Xi(t)进行估计,需要对滤波方程进行扩展。

系统状态空间方程

X(k)=ΦX(k-1)+Гω(k-1)

(32)

观测方程

Z(k)=HK(k)+Dω(k)+ε(k)

(33)

式中,ω(k)和ε(k)分别为系统噪声和观测噪声,假设与1.2节相同。

令

υ(k)=Dω(k)+ε(k)

(34)

则观测方程为

Z(k)=HX(k)+υ(k)

(35)

将以上结果代入式(10)～式(16),得到

(36)

G(k-1)=ΓQ(k-1)DT+
[DQ(k-1)DT+R(k-1)]-1

(37)

P(k/k-1)=[Φ-G(k-1)H]P(k-1/k-1)·

[Φ-G(k-1)H]T+ΓQΓT-G(k-1)DQΓT

(38)

J(k)=HP(k-1/k-1)HT+DQDT+R

(39)

Ka(k)=P(k/k-1)HTJ-1(k)

(40)

P(k/k)=[I-KaH]P(k/k-1)

(41)

(42)

(43)

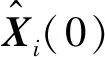
(44)

求得

(45)

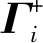
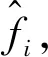
(46)

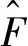
(47)

以上就是基于卡尔曼滤波算法的载荷识别具体过程。

绘制出基于卡尔曼滤波算法的动荷载识别流程图如图1所示。

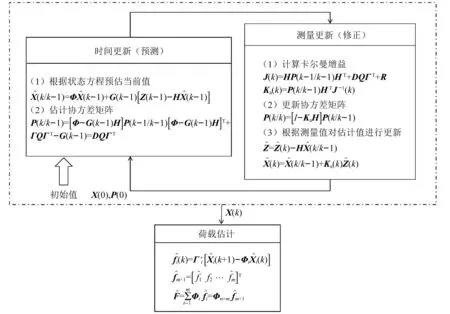
图1 基于卡尔曼滤波器的荷载识别原理Fig.1 Load identification principle based on the Kalman filter

2.2 云模型优化的离散卡尔曼滤波动荷载识别

在实际测量中,结构的动力测量响应会受到噪声和误差等问题的干扰,进而导致荷载识别结果产生较大偏差,因此仅仅利用该方法进行荷载识别难以处理噪声和误差带来的干扰问题。因此,本文采用云模型理论来解决此类干扰问题。云的生成的具体算法称为云发生器[14],可以分为正向云发生器和逆向云发生器,其中,逆向云发生器通过输入一定数量的云滴求出云模型的3个数字特征。本文利用多次荷载识别结果生成云滴,借鉴逆向云发生器的原理产生云的3个数字特征,解决测量误差及噪声带来的干扰问题。具体过程如下:

(1)根据每个时刻n次采样数据的识别结果计算该组数据的样本均值为

(48)

一阶样本绝对中心距

(49)

样本方差

(50)

(51)

(52)

(53)

(3) 利用数字特征计算确定度μ

(54)

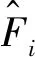
(4) 利用确定度确定识别值

由云模型性质可知,该点确定度越高,则越接近云的期望值,而期望值是云的中心位置反映在云图横坐标上的值,表示该点在论域中最能够代表定性概念,所以本文计算每一时刻每次采样数据的识别结果对应的确定度μ,此时求得n个μ,然后选取其中的最大值对应的识别值,表示该识别值最接近该时刻真实的荷载值,其余时刻以此类推。

通过图2可以进一步理解如何利用确定度确定识别值。图2中:纵轴为某时刻识别值的确定度大小;横轴为该确定度对应的荷载大小,确定度最大的点对应的荷载值即为本次识别最终的识别值。

图2 某时刻识别值的确定度Fig.2 Determination of the recognition value at some time

综合本节内容,建立基于云模型优化的卡尔曼滤波的荷载识别处理策略如下:

(1)进行多次测量,获取多次含测量噪声的结构动力响应数据。

(2)将动力响应数据代入基于卡尔曼滤波的荷载识别算法程序,多次采样数据得到多个识别结果,从而构造出包含多个云滴的云模型。

(3)计算所有云滴的数字特征,即期望、熵和超熵,并计算每个时刻识别值的确定度。

(4)根据每个时刻识别值确定度的大小确定最终识别值,确定度最大的点对应的荷载即为本次的荷载识别值。

3 数值仿真

3.1 有限元建模

为了验证本文提出的基于云模型和卡尔曼滤波的动荷载识别方法的有效性,本文针对具体实际工程临时看台结构建立有限元模型,设置多种荷载类型和噪声水平进行数值仿真。

某比赛赛场临时看台结构如图3所示,看台支撑结构为承插型盘扣式钢骨架,立杆纵向距离为2.0 m,横向距离为2.4 m,看台首排高度为1 m,后排高度为8.0 m。看台主体由承插型盘扣式钢骨架、看台板及其下部的三角形桁架、栏杆和通道体系组成,立杆底座采用槽钢固定至楼板。本文仅针对承插型盘扣式钢管骨架进行研究。

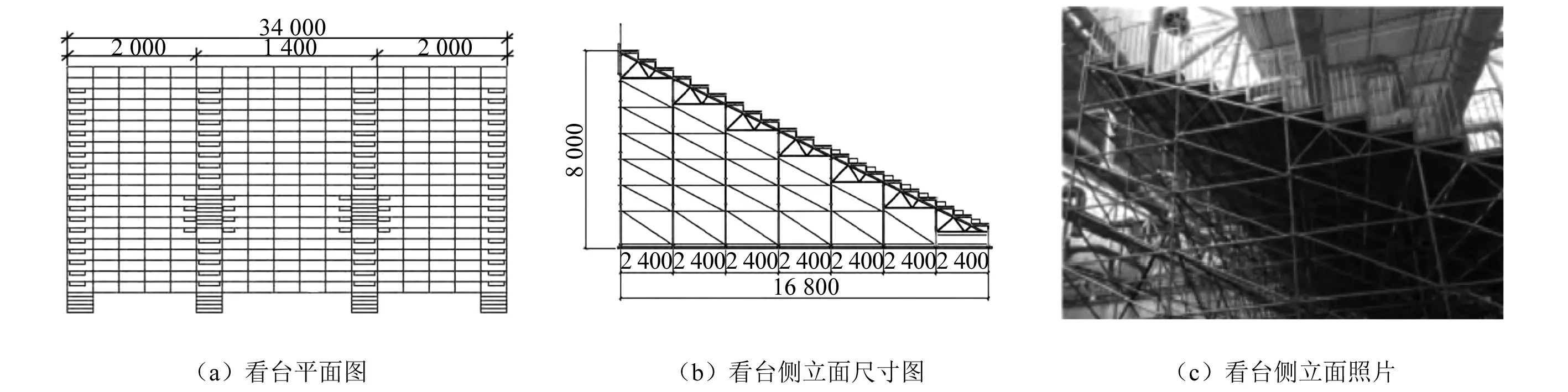
图3 某比赛赛场临时看台结构[15](mm)Fig.3 Structure of temporary stand for a competition field (mm)

临时看台结构所用钢材为Q345B,弹性模量为E=2.06×1011Pa,泊松比为0.3,密度7 850 kg/m3。杆件的截面属性如表1所示。表1中:P和B分别代表圆钢管和方钢管。

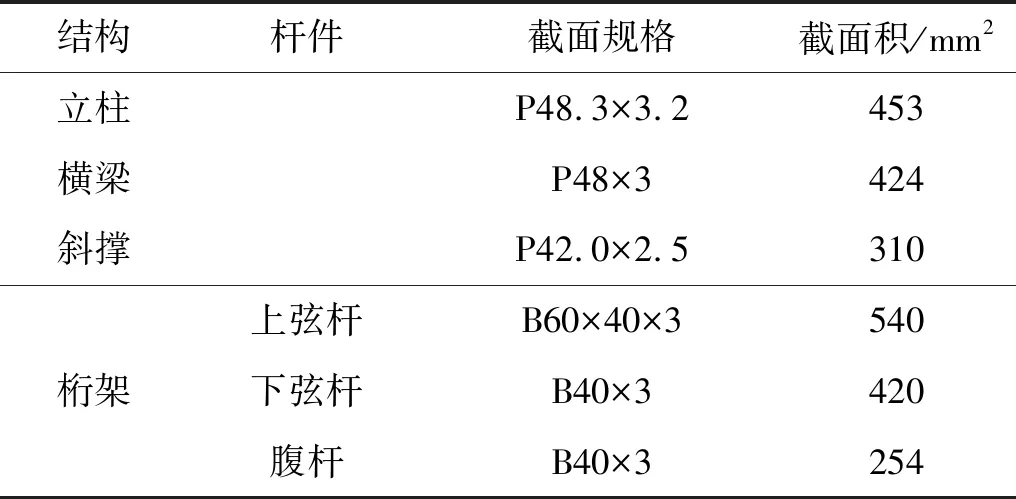
表1 杆件截面属性

由JGJ 231—2010《建筑施工承插型盘扣式钢管支架安全技术规程》[16]可知承插型盘扣式钢管骨架结构本质上是一种半刚性空间框架钢结构,水平杆与立杆之间介于铰接与刚接之间的一种连接形式,设计时可以偏于保守的将骨架结构考虑为钢桁架形式,即可以将半刚性节点按铰接建模。因此,将看台骨架结构简化为节点铰接,底部固接的结构。为了简化计算,本文仅选取部分看台支撑结构作为研究对象。本文利用ABAQUS软件中的T3D2H桁架单元创建临时看台支撑结构模型如图4所示。

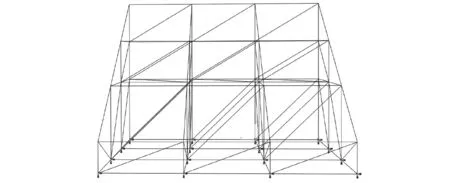
图4 临时看台支撑结构简化模型Fig.4 Temporary stand support structure simplified model

3.2 参数和工况设置

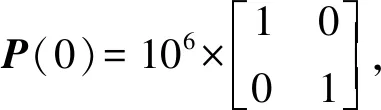
定义时程计算工况为:分析时长为10 s,分析时间步长0.001 s,输出时间步长1 000步;定义荷载工况依次为正弦荷载、方波荷载、锯齿荷载以及多个正弦叠加荷载作用在临时看台上表面,假设荷载作用方向竖直向下,并且每个节点均匀分担荷载;测点布置如图5所示,即本文数值模拟是通过该16个节点的竖向位移响应进行看台动荷载识别,看台节点竖向位移时程如图6所示。

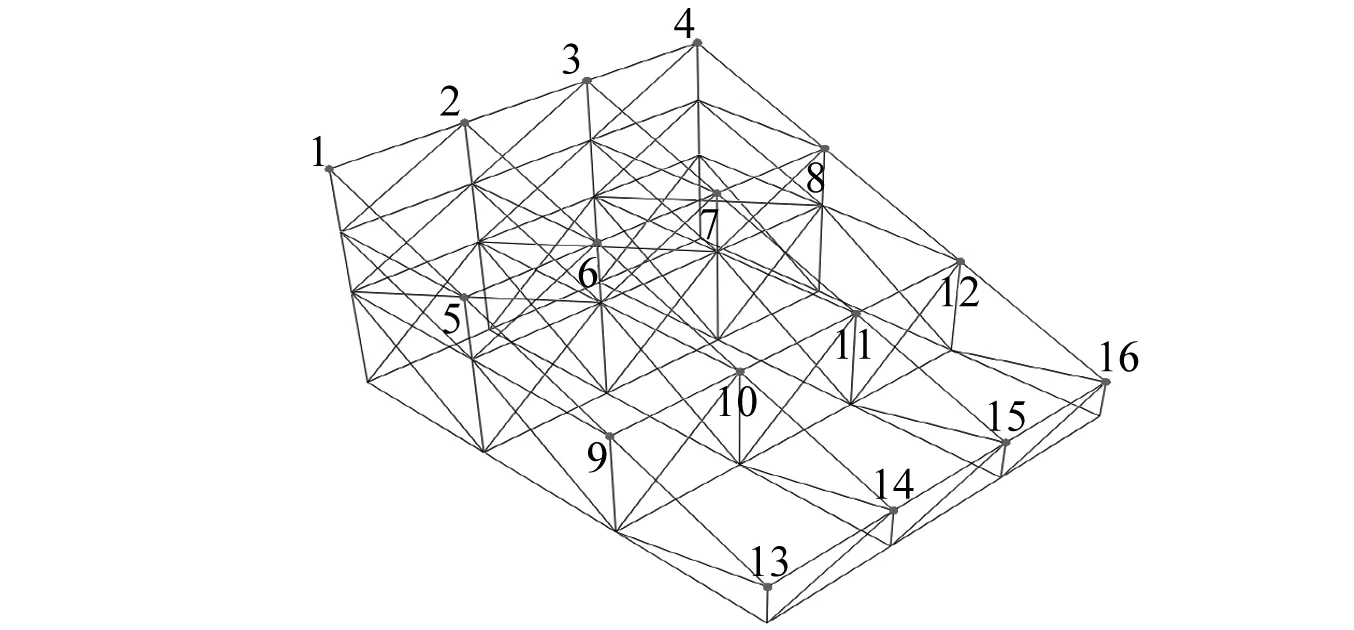
图5 测点布置图Fig.5 Measuring point layout

图6 节点竖向位移时程图Fig.6 Time history diagram of node vertical displacement

另外,为了验证该方法在位移响应的鲁棒性,将在观测响应中混入高斯白噪声,噪声施加方式如下

(55)

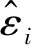
3.3 荷载识别结果分析

为验证本文提出的云模型优化卡尔曼滤波的荷载识别方法在荷载识别中具有更高的精度,选择与基本离散卡尔曼滤波荷载识别方法进行对比。以下将从荷载时程和标准均方根误差两个角度评估荷载识别精度。由于篇幅限制,仅选取节点5的识别结果进行展示,如图7所示。其余节点识别效果与节点5类似。

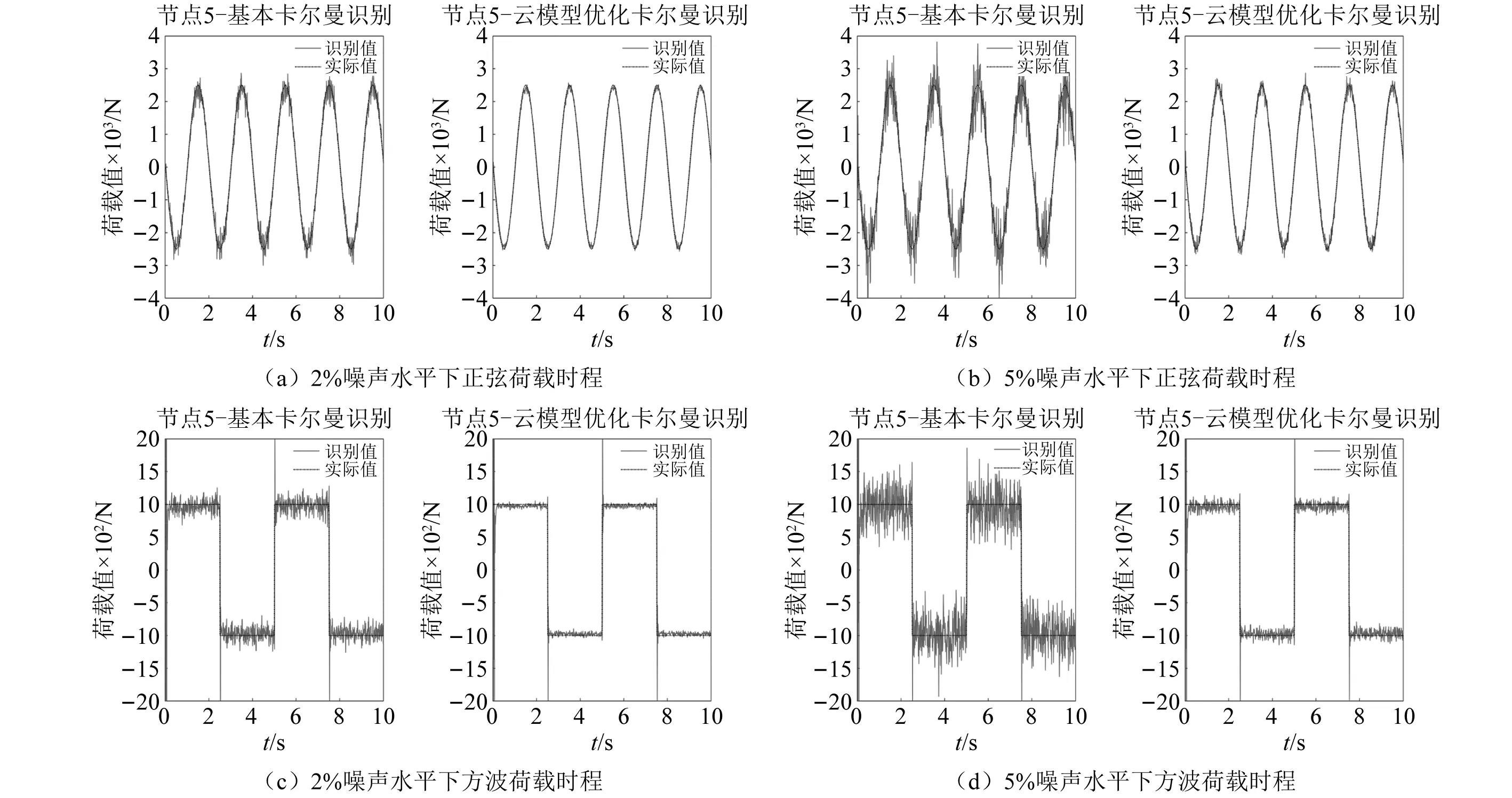
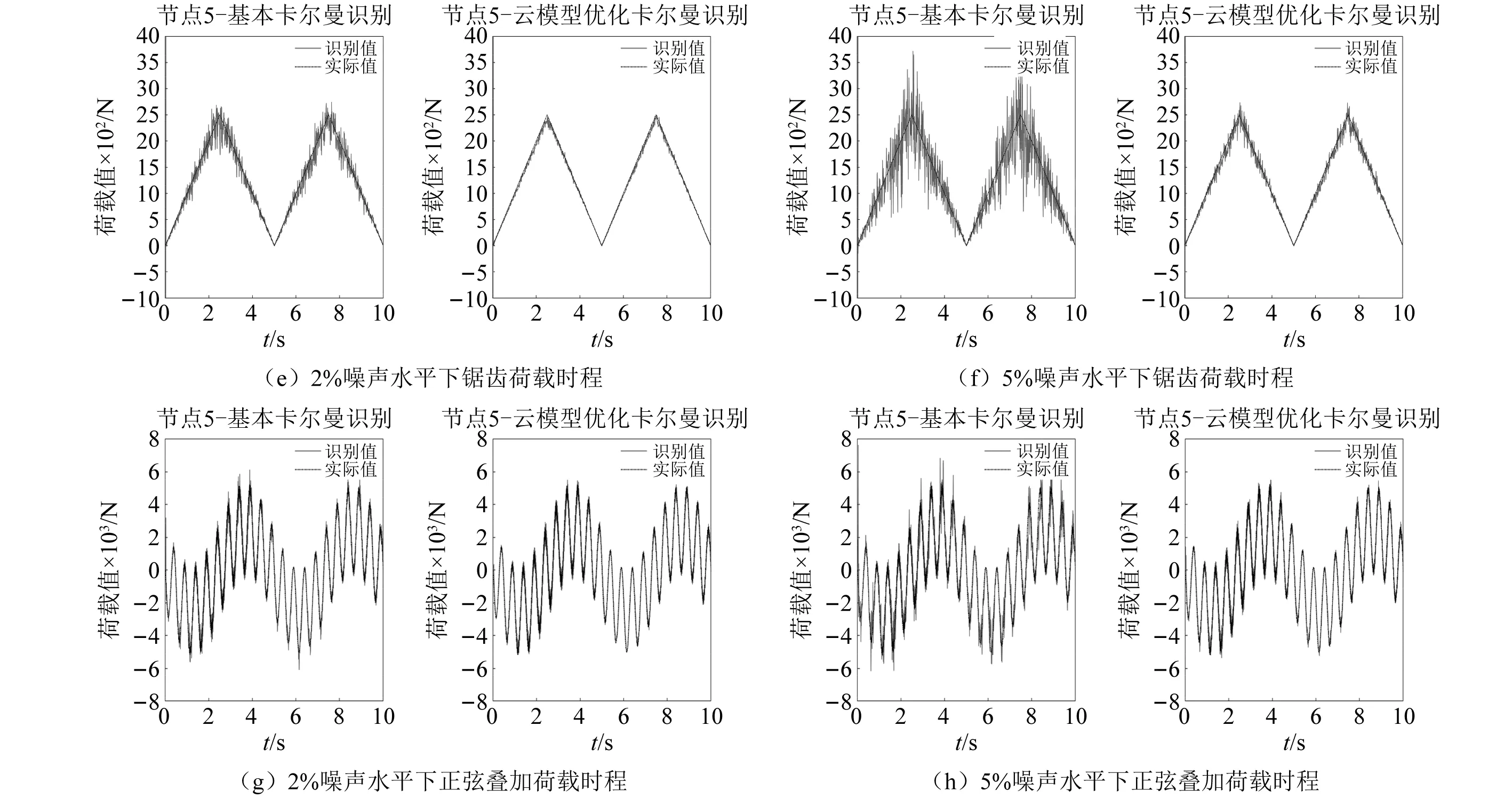
图7 荷载识别结果时程图Fig.7 Load identification result time course chart

为了评估荷载识别的精度,本文将采用标准均方根误差(normalized root mean square error,NRMSE)来量化误差,其表达式如下

(56)

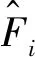
由于噪声的生成具有随机性,为了更好地评价该方法的荷载识别性能,对每个噪声工况独立运行5次并求均值。该过程采用MATLAB编程实现,结果如表2所示。

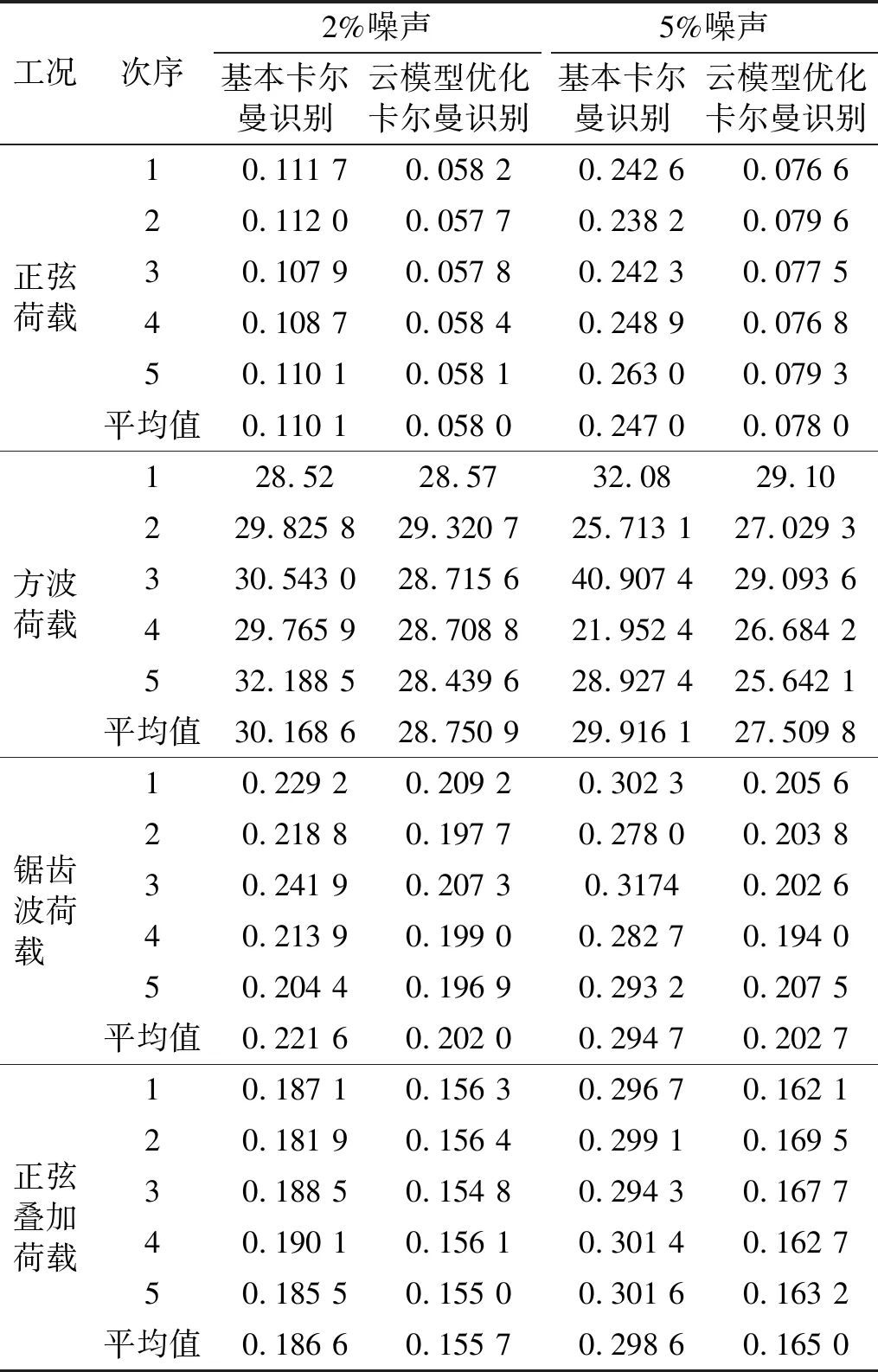
表2 不同噪声水平下荷载识别的NRMSE值

本文提出的云模型优化卡尔曼滤波荷载识别算法识别精度高,且该方法对计算硬件要求较低,计算速度与基本卡尔曼滤波方法接近。通过对结构位移响应信号施加不同水平的噪声及其荷载识别效果图可以看出该方法具有较好的稳定性及误差处理能力。对看台结构模型依次施加正弦、方波、锯齿波以及正弦叠加荷载进行数值仿真,结果表明:正弦荷载识别效果最优,而后依次为正弦叠加荷载、锯齿波和方波荷载。由图6可知方波和锯齿波荷载在曲线转折处识别误差较大,尤其是方波的初始点和转折处误差很大,导致NRMSE值过大,但平缓荷载处识别效果明显较好,这是由于荷载突变处对识别算法的实时追踪能力要求较高。

由表2的NRMSE值可知,本文所建议的云模型优化卡尔曼滤波方法的识别误差普遍小于基本卡尔曼滤波的荷载识别算法。随着噪声水平的升高,本文方法的NRMSE值变化较小,仍旧保持良好的识别性能,说明该方法具有良好的抗噪性能。

4 结 论

本文提出了一种基于云模型和离散卡尔曼滤波的动荷载识别方法。为了验证该方法对看台结构荷载识别的有效性,本文采用了简化的临时看台结构模型进行数值仿真,并与基本离散卡尔曼滤波的荷载识别方法进行了对比。通过不同类型荷载识别的对比结果可看出所建议方法具有良好的稳定性和较好的处理能力;另外,本文设置了2%和5%两种噪声水平,可以看出随着噪声水平的升高,基于卡尔曼滤波方法的识别结果出现明显偏差,荷载时程曲线拟合程度降低,标准均方根误差值也随即增大,而本文提出的方法受噪声影响较小,仍保持着良好的识别性能。因此,本文提出的基于云模型和离散卡尔曼滤波的动荷载识别方法识别精度较高,抗噪性良好,而且和基本卡尔曼滤波方法类似,具有一定的在线监测荷载的功能,故具有较好的工程应用前景。