黄土地区既有多股道运营铁路架空体系动力特性研究

张玉伟, 周鹏远, 宋战平, 王 剑, 刘 奇

(1.西安建筑科技大学 土木工程学院, 西安 710055;2.西安建筑科技大学 陕西省岩土与地下空间工程重点实验室, 西安 710055;3.中铁二十局集团有限公司, 西安 710016)

随着城市化进程的加速发展,新建交通路线往往会下穿既有运营路线,如何在新建线路安全施工的同时保证既有线的安全运营成为此类工程的重难点[1-4]。目前新建线路下穿既有运营线常采用既有运营线架空的施工方法,架空体系既需要保障既有运营线路的运营要求,还要同时满足新建线路的施工要求。因此,架空体系既受到既有运营列车动荷载的影响,同时还受下方新建线路施工扰动带来的不利作用,架空体系的稳定性至关重要[5-7]。研究新建线路施工扰动条件下架空体系受运营列车动荷载的影响,并评价架空体系的安全性,对新建线路的施工安全和既有运营线的运营安全都具有重要意义。

运营列车动荷载对下方结构物影响明显,一直以来,各国学者就列车动荷载对下部结构物影响方面开展了诸多研究。前期的研究基本上都是运用解析、半解析法计算列车荷载作用下地面振动响应[8-9]。随着计算机技术的发展和各精密仪器的制造,之后又出现了诸如有限元法[10]、振动台比对试验法[11]、数值模拟[12]等方法,同时也出现了一些借鉴行比较强的理论方法。基于各种方法,前人就各建(构)筑物在列车动荷载影响下的响应进行了一系列研究,如Balendra等[13]采用波函数展开法,研究了列车作用下隧道-土-建筑系统的相互作用。Thusyanthan等[14]对装有微型加速度计的小型模型隧道进行了动力响应试验,并提出了能量传输比与土壤与隧道衬砌阻抗失配比的关系式。杨文波等[15]采用模型试验与数值模拟相结合的方法,研究了隧道管片和内部结构的动力响应特性以及振动波在地层中的衰减特性。白冰等[16]利用有限元数值方法,分析了单列列车荷载以及双列列车荷载作用下土体-隧道结构体系的加速度和内力响应时程曲线。Zhang等[17]采用试验建模的方法,探讨了相邻平行盾构隧道在不同列车激振荷载作用下的相互作用。Yang等[18]通过物理模型试验,研究了长期列车荷载对隧道衬砌和周围土壤动力响应的影响,得出来不同加载循环作用下计算模型的峰值颗粒加速度和频率响应函数。黄强等[19]对车辆-轨道-隧道-地基模型进行详细分析,给出轨道平顺与否条件下列车荷载的简化模型。Di等[20]提出了一种改进的隧道模型,用于评价饱和土体中的列车动应力响应。王道远等[21]综合考虑列车荷载、埋深、土体弹性模量等因素,采用数值模拟方法分析了地表沉降规律,建立了地表最大沉降量预测公式。综上所述,列车荷载对既有建(构)筑物有明显影响,目前有关列车荷载作用下既有铁路线架空体系动力特性影响的研究较少,特别是大断面管涵顶进施工的研究较为不足,因此,需要深入研究大断面管涵顶进施工中列车荷载对既有线架空体系的动力稳定性影响,并对其安全性进行综合评估。

基于此,本文基于西安市经九路下穿陇海铁路立交工程5#箱涵顶进段架空工况,针对既有运营铁路架空转换中架空体系的受力问题,利用数值模拟和现场监测方法开展系统研究。在确定列车几何、轴重等参数的基础上,对两股道既有线上不同行车速度及不同轴重列车荷载作用下既有线架空体系的动力响应规律进行了数值模拟分析,同时现场监测了架空体系的动力加速度,并与数值模拟结果进行对比验证。最后对京九路下穿陇海铁路的架空体系的稳定性进行了评估,研究结果对类似下穿工程具有指导意义。

1 依托工程概况

1.1 工程背景

西安市经九路—陇海铁路立交工程南起西安市长缨路,向北依次下穿华清路、陇海铁路、规划一路,最终与含元路平交,全长1.13 km,研究区间位置如图1所示。起止里程号为K0+480～K0+575,与陇海铁路以26.55°斜交,立交桥下穿铁路既有轨道共计5股,分别为陇海下行线、新建车底走行线1股道、新建机车走行线2股道、改建陇海上行线。

图1 工程位置示意图Fig.1 Schematic diagram of project location

立交桥下穿铁路段为(4.5 m+5.0 m+15.5 m+15.0 m+4.5 m)钢筋混凝土结构,沿经九路道路中心全桥长95 m。西侧长109.24 m,东侧长84 m,总体俯瞰呈梯形,正交宽度50.5 m,斜交宽度56.45 m。立交桥整体共分为9节框架箱涵,由南向北依次划分为第1～第9节段。其中,第1、第5节段采用预制顶进法施工,预制第1节段框架箱涵的工作坑位于陇海下行线南侧,由南向北顶入施工下穿陇海下行线;第5节段下穿新建陇海上行线和新建机车走行线右线,预制工作坑在拆除车辆段线和北郊专用线后置于陇海上行线北侧,由北向南顶入施工。第4节段采用线下架空现浇法施工,第2、第3、第6～第9节段采用原位现浇法施工,1～9号框架箱涵与既有5股道平面位置关系如图2所示。工程涉及到目前西北地区横断面最大的箱涵结构,本文以5#箱涵架空顶进施工开展研究,进行多股道运营铁路架空体系动力特性分析。

图2 现场平面布置图(mm)Fig.2 Site layout plan(mm)

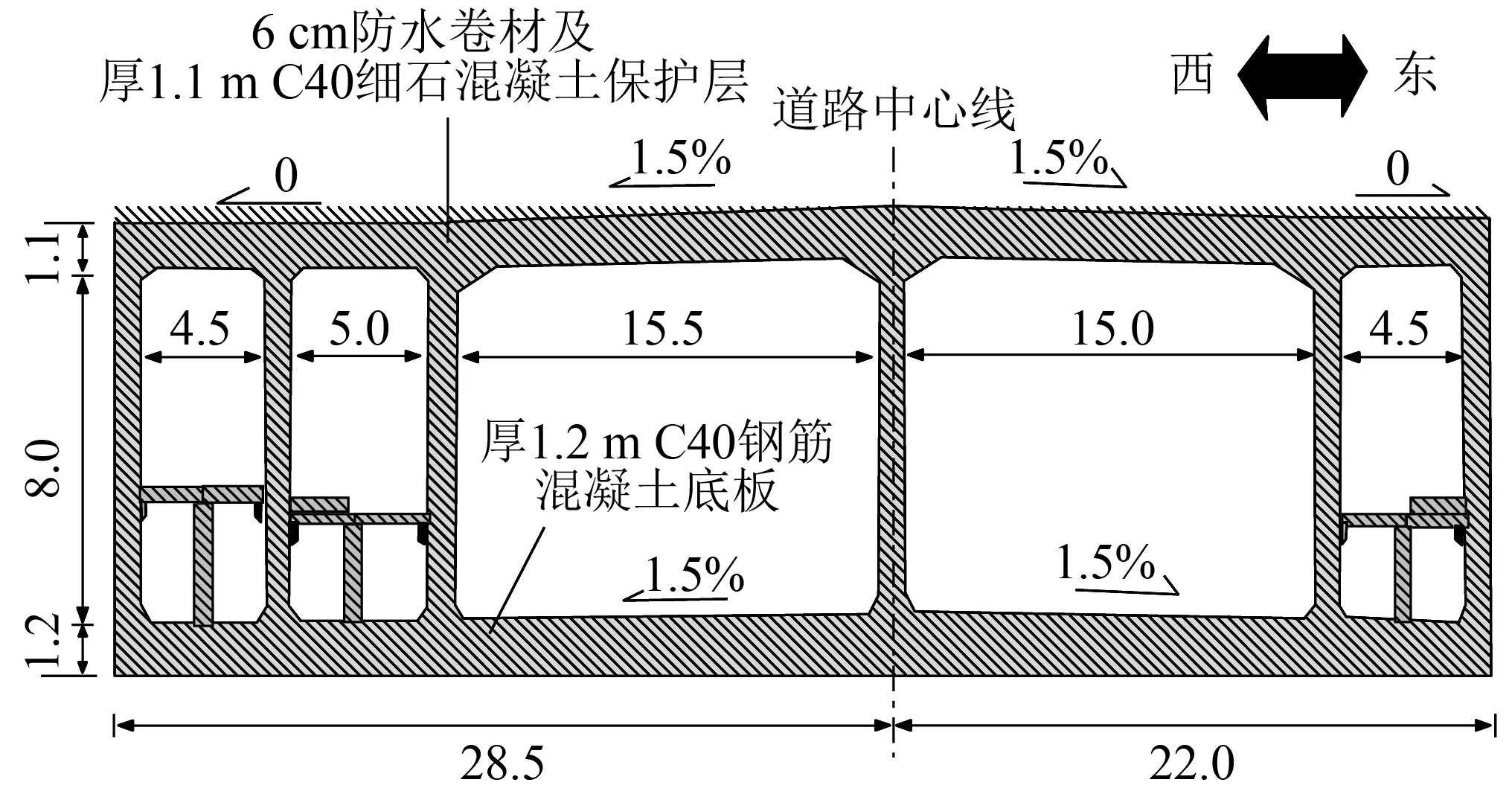
图3 5#箱涵结构图(m)Fig.3 Structural drawing of 5# frame box culvert(m)

1.2 工程地质与水文地质条件

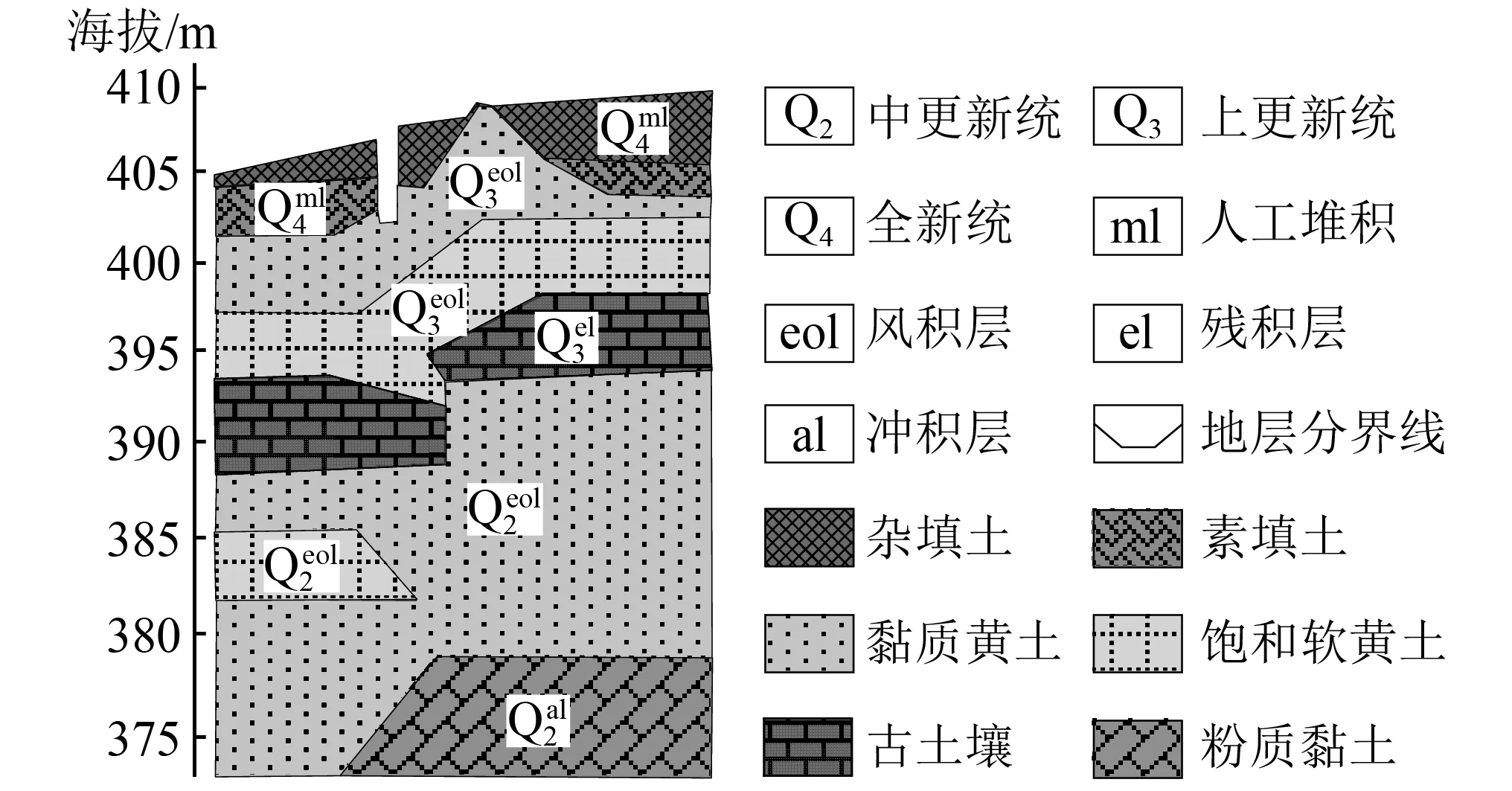
图4 依托工程区间地质剖面图Fig.4 Interval geological section of the supporting project

工程所在区域地几乎无地表水,地下水为第四系孔隙潜水,地下水补给主要有大气降水、侧向径流及局部水管渗漏等,地下水位埋深约9.80～13.50 m,对应高程394.34 ～397.90 m。根据水质分析报告,工点范围内地下水对混凝土具有硫酸盐及氯盐侵蚀性,环境作用等级为H1,L1。

1.3 既有线架空体系

由于工程所处地下水位在原地面以下13 m,水位线以下为饱和软黄土不良地质。现场选取了2根L=23 m Φ1.25 m基坑支护桩作为人工挖孔试桩进行试验,由于水位线以下土质饱和度大于100%,处于流溯状态,无法成桩,所以在降水施工后再进行人工挖孔施工,降水深度大于12 m。

在各箱涵施工前,进行:①过渡架空,对既有线进行过渡架空,采用直径1.25 m,长12 m人工挖孔桩,7跨跨径16 m的I100工字钢梁连续架空;②架空施工完成后,在基坑东西两侧施作拉槽;③在拉槽内施作直径1 m、深18 m、间距1.5 m的支护桩,施作冠梁,形成预支护,并在拉槽内施作降水井;④正式架空的人工挖孔桩施工,采用桩径1.5 m、长24 m、间距8 m的人工挖孔桩,混凝土护壁逆作法施工。架空桩与箱涵平面及立面位置关系如图5所示。现场架空施工图,如图6所示。

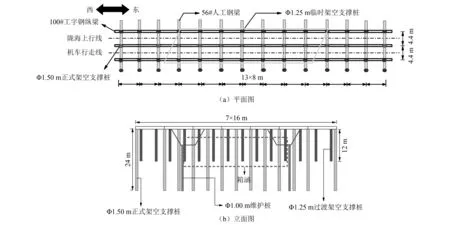
图5 架空桩布置示意图Fig.5 Layout of pile installation of overhead support

图6 现场架空施工图Fig.6 Site overhead construction

本工程各段箱涵施工顺序为:①先进行5#预制箱涵顶进施工;②然后进行1#预制箱涵顶进施工;③当5#和1#箱涵顶进施工完成后,进行2～4#箱涵原位现浇;④当1～5#箱涵施工完成后,进行6～9#箱涵的原位现浇。由于本项目采用了临时架空桩到正式架空桩的转换体系,正式架空桩未投入工作前的临时架空桩工作时为最不利工况,因此本文选择临时架空体系中5#箱涵顶进施工完成时的工况为研究对象,开展列车荷载影响下的动力分析。

2 架空体系动力响应数值模拟

2.1 数值模型及边界条件

本文借助Revit对结构模型稍作简化后,导入Midas GTS得到实体模型。当整体模型范围取3倍～5倍的结构尺寸时可基本消除边界条件的影响,因此,为满足有限元分析精度要求,本文取模型整体尺寸长150 m、宽 130 m、高50 m,地层由上至下主要包括杂填土、素填土、黏质黄土层、饱和软黄土层、古土壤层、粉质黏土层。架空体系按照前述描述进行设置,桩长为12 m,间距为8 m,桩径为1.25 m。

数值模拟中,根据实际列车型号,赋予轴间距和轴荷载具体数值来定义列车类型,同时将列车动力荷载要通过的节点选择,并指定开始和结束节点,从而模拟列车荷载的施加过程。对于研究列车振动荷载的动力计算,网格数量会影响到计算时长。对于网格单元尺度范围对计算结果质量的影响,通过廖振鹏[22]的研究可知,为保证计算精确度,应将网格单元的长度保持在1/8～1/6计算波长内。据此提出了以土的剪切波长λs作为网格尺寸Δl控制的要求,如式(1)

(1)

考虑到实际工况中研究内容的主次之分,为防止网格单元数过多而无法求解运算,优先将架空结构、轨道路基及箱涵等靠近振源范围内的网格进行精密划分,远离中心影响范围的土层结构适当粗分。根据以上方法,最终5#箱涵顶进架空段共划分为232 734个六面体单元,171 035个节点,路基及周围土层均采用摩尔-库伦准则,架空及铁路结构均采用弹性准则,架空体系与地层和箱涵结构接触关系均设置界面单元,数值模型,如图7所示。

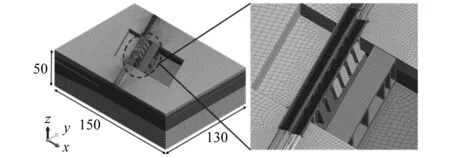
图7 有限元数值模型(m)Fig.7 Finite element numerical models under two working conditions(m)

2.2 模型参数选取

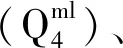
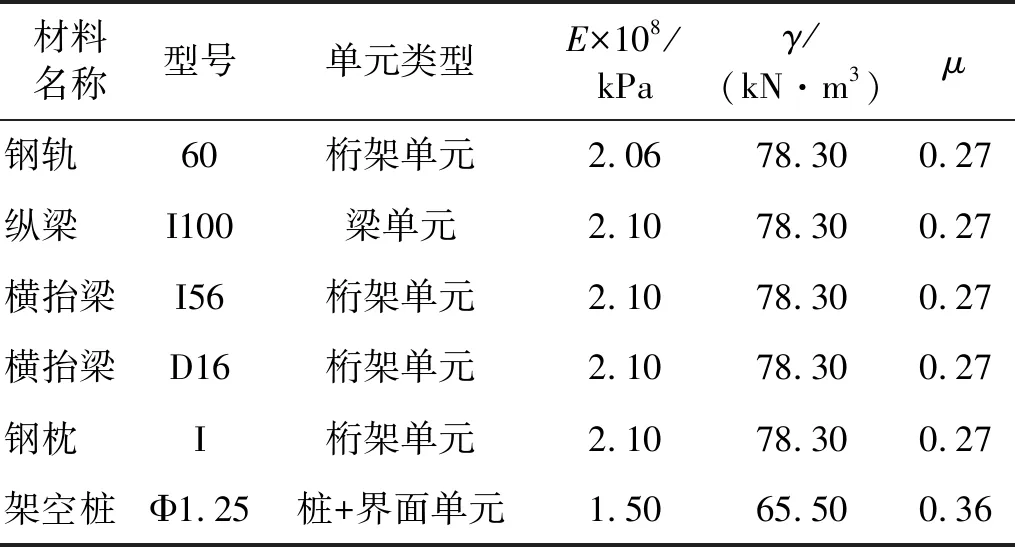
表1 架空结构物理力学参数

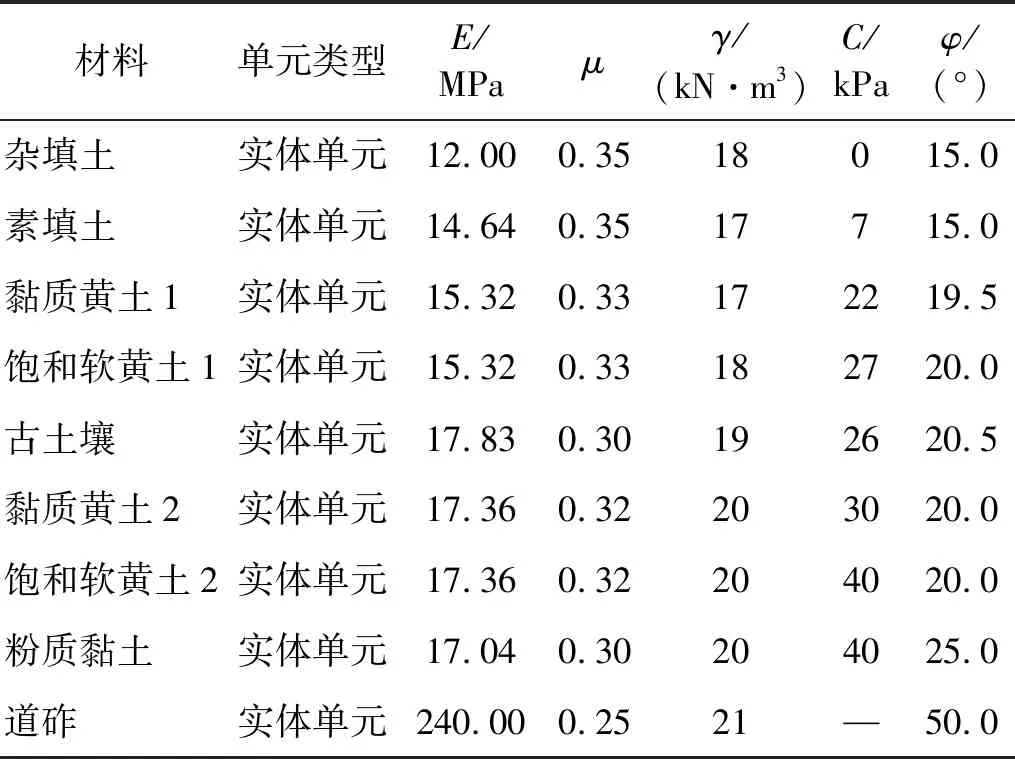
表2 土体物理力学参数

2.3 研究工况

陇海线运营列车包括客车和货车,列车满载与空载条件下标准轴重荷载分别为147 kN(15 t)和107.8 kN(11 t),为分析满载和空载两种情况下架空施工动力响应规律,数值分析中取满载荷载150 kN、空载荷载110 kN进行模拟。另外,考虑到施工影响,列车运营速度限速60 km/h,则本文分别以列车轴重为110 kN,150 kN,列车运行速度分别为30 km/h,60 km/h的各组合为工况进行模拟分析,研究既有线架空结构的动力响应规律,分别讨论行车速度和列车轴重对结构动力响应的影响。

根据现场施工工况,临时架空体系下方为有序掏槽布置,故三维有限元模型选取其中一组作为典型分析工况,分别监测钢枕、横抬梁和架空桩的动力特性,用测点一、测点二、架空桩端和横抬梁表示测点位置,测点位置示意图如图8所示,钢枕1为测点一,钢枕2为测点二,需要注意的是横抬梁在临时架空体系下尚未进入工作状态,在正式架空后的箱涵顶进过程中才正式工作,因此本文分析不考虑横抬梁动力响应。

图8 架空结构特征点示意图Fig.8 Schematic diagram of feature points of overhead structures

3 数值结果分析及讨论

3.1 不同车速下架空结构动力响应

不同车速下架空结构动力响应计算条件:陇海铁路上行线单线加载,列车轴重取110 kN,选择列车运行速度分别为30 km/h和60 km/h时进行动力响应对比研究,考虑列车长度及运行速度,计算时长取一趟列车通过的时间分别取35 s和20 s。

3.1.1 加速度响应分析

不同列车运行速度下各测点的加速度时程曲线变化规律如图9所示。由图9可知,在不同列车运行速度下,相同测点的振动加速度时程曲线变化规律趋势相似,加速度响应都是随着时间的增加而上下波动并在宏观上出现逐渐衰减现象。并且随着列车运行速度的增加各特征分析点的振动加速度幅值会相应增大。当列车运行速度从30 km/h变化到60 km/h时,测点一加速度时程曲线的峰值分别为1.46g和1.95g,加速度峰值增加约33.6%;测点二加速度时程曲线的峰值分别为1.26g和1.83g,加速度峰值增加约45.3%;架空桩加速度时程曲线的峰值分别为0.19g和0.48g,加速度峰值增加约125.3%。可以看出,在相同列车运行速度下,架空结构不同位置处振动加速度响应也存在着较为明显的差异,统一表现为测点一较大,测点二次之,架空桩端最小。钢枕的动力响应要比架空桩大差不多一个数量级,但对于列车速度变化影响下的加速度幅值变化速率方面,可以看出,相对于钢枕,架空桩对列车速度的变化更为敏感。

图9 不同行车速度下架空结构各测点加速度时程曲线Fig.9 Acceleration time history curves of each measuring point of overhead structure under different driving speeds

列车荷载作用下,架空结构的钢枕部位处的振动加速度响应相比其他部位尤为明显。在列车变化情况下,钢枕部位变化基本可以忽略,但架空桩对于列车速度变化的影响较为明显,如果上部列车速度有变化,应更关注于架空桩部分。但无论列车速度为30 km/h或是60 km/h,在整个列车运行过程中,全部测点所产生的振动加速度峰值不大,对架空体系的影响较小。

3.1.2 位移响应分析

不同列车运行速度下各测点的竖向位移时程曲线变化规律,如图10所示。与振动加速度规律相同,在不同列车运行速度下相同测点的竖向位移时程曲线变化规律趋势相似,位移响应都是随着时间的增加而上下波动并在宏观上出现逐渐衰减现象。由于列车速度不同,施加的荷载也不同,并且随着列车运行速度的增加各特征点的竖向位移幅值会相应增大。当列车运行速度从30 km/h变化到60 km/h时,测点一竖向位移时程曲线的峰值分别为-5.23 mm和-6.58 mm,位移增加约25.8%;测点二竖向位移时程曲线的峰值分别为-4.72 mm和-6.17 mm,位移增加约30.7%;架空桩测点竖向位移时程曲线的峰值分别为-3.17 mm和-3.85 mm,位移增加约21.5%。不同速度下钢枕测点一的竖向位移响应最为明显,测点二的竖向位移响应与之相差不大,而架空桩测点的竖向位移响应最小。同时可以看出,对于列车速度变化的敏感性方面,钢枕位移和架空桩位移对于速度变化的敏感性差别不大。

图10 不同行车速度下架空结构各测点位移时程曲线Fig.10 The displacement time history curves of each measuring point of overhead structure under different driving speeds

无论列车速度为30 km/h或是60 km/h,全部测点所产生的竖向位移峰值在铁道及架空结构容许范围值内,由此说明,上述情况下运行列车对架空结构产生的竖向位移较小,整个架空体系较为安全。

3.1.3 动应力响应分析

不同列车运行速度下各特征点的轴应力时程曲线变化规律,如图11所示(正值表示受拉,负值受压)。可以看出,当列车以不同速度通过测点位置时,架空结构同一测点的动应力时程曲线变化规律相似,不同之处在于当行车速度为60 km/h时,对于钢枕测点,在列车行驶后期其轴应力衰减较快,而架空桩在不同速度下的轴应力响应没太大变化。对于轴应力峰值方面,当列车速度由30 km/h变化到60 km/h时,测点一总体表现为处于受拉状态,轴应力峰值从754.40 kN/m2变为795.54 kN/m2,增加约5.5%;测点二总体表现为处于受拉状态,轴应力峰值从684.99 kN/m2变为724.41 kN/m2,增加约5.8%;架空桩测点总体表现为受压状态,轴应力峰值从-55.21 kN/m2变为-74.40 kN/m2,增加约34.8%。根据分析可知,钢枕可视为假设在路面的梁结构,当上部有列车荷载时,其受力边表现为受拉,而由于测点一远离横抬梁,受到横抬梁较小的约束影响,故测点一应力幅值要略大于测点二;而架空桩在上部列车荷载和钢枕自重下,表现为受压状态,但由于上部钢枕及横抬粱等结构作用,以及桩周围土体对于上部荷载的承载作用,使得桩所受压应力较低。

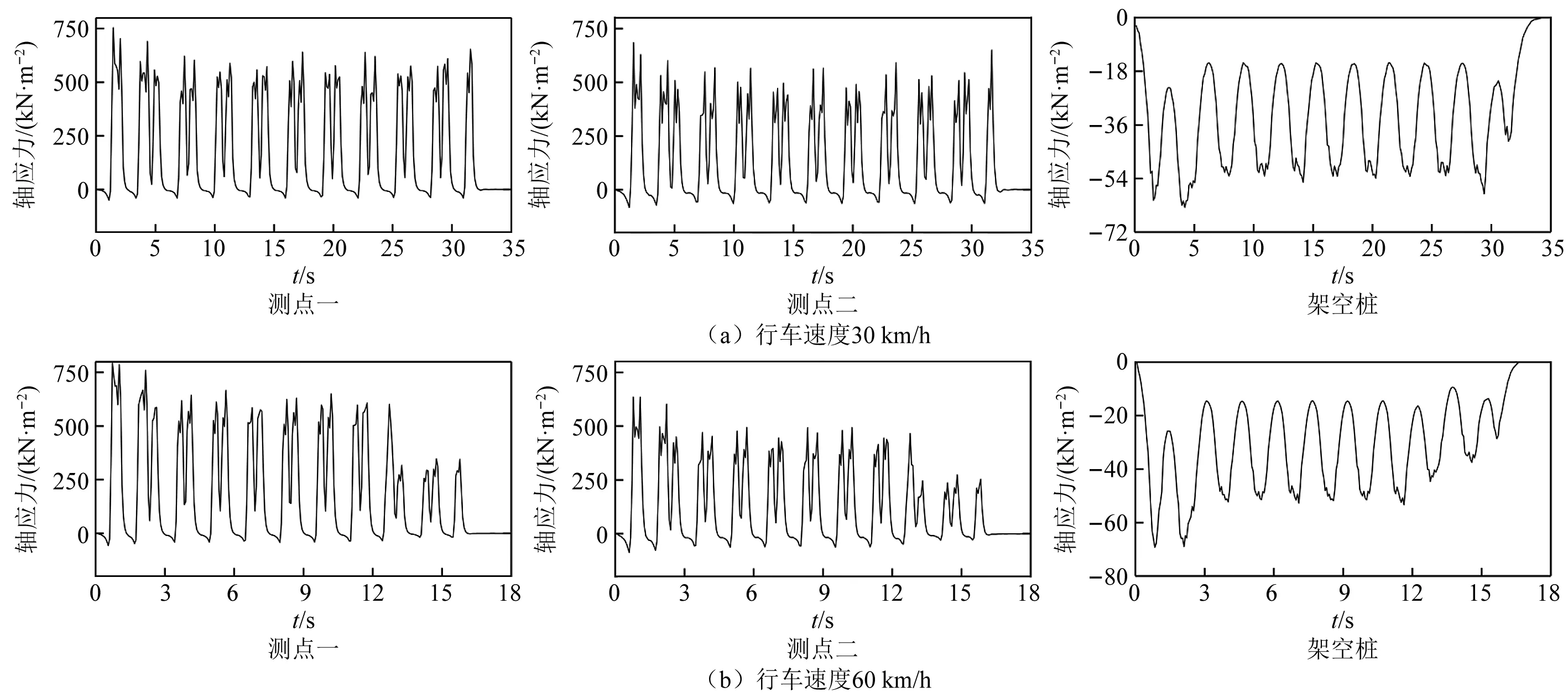
图11 不同行车速度下架空结构测点一动应力时程曲线Fig.11 Time-history curves of dynamic stress at measuring point 1 of overhead structure at different running speeds

总的来说,当列车通过架空结构测点位置时,架空结构的拉、压应力远小于架空结构材料的强度限值,因此,该工况列车荷载作用下不会对架空结构安全性造成破坏。

3.2 不同轴重下架空结构动力响应

不同轴重列车荷载作用下架空结构动力响应计算条件:陇海铁路上行线单线加载,列车轴重取110 kN和150 kN。由于本工程段上部列车行驶速度一般为45 km/h左右,因此本节选取列车运行速度45 km/h为固定参数。考虑列车长度及运行速度,计算时长取一趟列车通过的时间为30 s。

3.2.1 加速度响应分析

不同列车运行荷载下各分析测点的加速度时程曲线,如图12所示。从加速度时程曲线可以看出,不同轴重下钢枕测点加速度响应幅值都呈现先减小后增大的规律,而架空桩加速度时程曲线波动较为平缓。同时,当轴重从110 kN变为150 kN时,测点一加速度峰值由1.67g变为2.01g,测点二加速度峰值由1.42g变为1.70g,架空桩测点加速度峰值由0.39g变为0.45g,各测点加速度变化较小,且数值也较低,就加速度响应而言,列车轴重的改变对于架空体系的加速度响应影响不大。

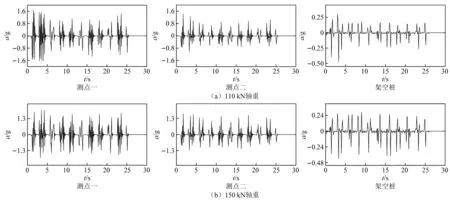
图12 不同轴重列车作用下架空结构各测点加速度时程曲线Fig.12 Acceleration time history curves of the overhead structure at each measuring point under the action of different axle load trains

3.2.2 位移响应分析

不同列车运行荷载下各分析测点的竖向位移时程曲线如图13所示。从加速度时程曲线可以看出,不同轴重下各测点竖向位移都表现为刚开始急剧增大,在第5 s左右会有所减小,之后20 s内曲线呈较为平稳状态,而在第25 s左右急剧减小。这分别对应于列车驶入、列车平稳运行和列车驶出阶段。而当轴重从110 kN变为150 kN时,测点一最大竖向位移由-6.29 mm变为-7.05 mm,位移增加约12.1%;测点二最大竖向位移由-5.96 mm变为-6.54 mm,位移增加约9.7%;架空桩测点最大竖向位移由-4.08 mm变为-4.33 mm,位移增加约6.1%。可以看出,轴重的改变对于列车竖向位移的影响可以忽略,同时在整个列车运行过程中,全部测点所产生的竖向位移峰值在铁道及架空结构容许范围值8 mm内,就竖向位移响应而言,架空结构较为安全。

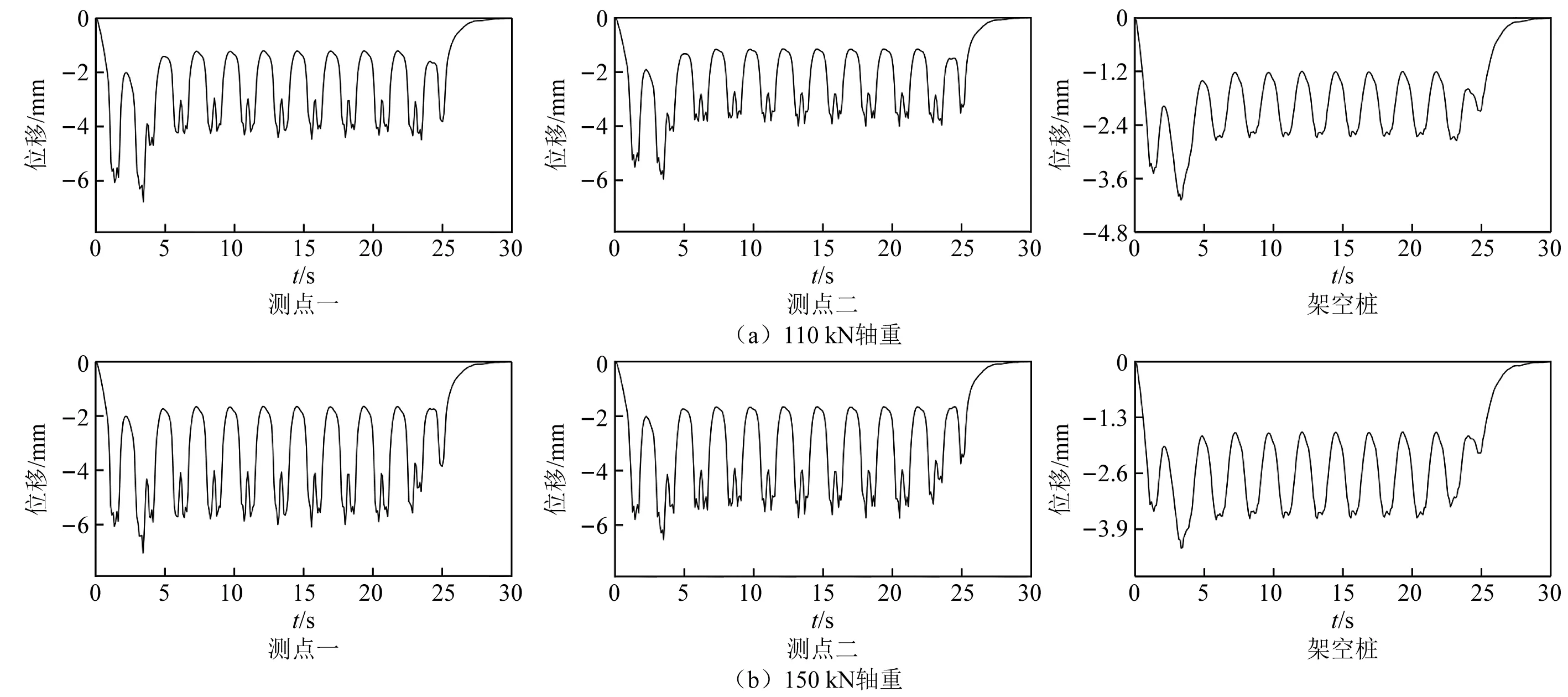
图13 不同轴重列车作用下架空结构测点一位移时程曲线Fig.13 Displacement time history curve of measuring point 1 of overhead structure under different axle load trains

3.2.3 动应力响应分析

不同列车运行荷载下各分析测点的轴应力时程曲线如图14所示。可以看出,不同轴重下,架空结构同一测点的动应力时程曲线变化规律相似。对于轴应力峰值方面,当列车速度由30 km/h变化到60 km/h时,测点一、测点二都表现为处于受拉状态,轴应力峰值从926.54 kN/m2变为921.79 kN/m2,测点二轴应力峰值均为815.18 kN/m2,架空桩测点受压且其轴应力峰值均为-77.27 kN/m2。显然,轴重的改变对于各架空体系测点整个阶段轴应力峰值影响几乎可以忽视。

图14 不同轴重列车作用下架空结构各测点动应力时程曲线Fig.14 The time-history curves of dynamic stress at each measuring point of overhead structure under the action of different axle load trains

但在列车平稳行驶阶段(即5～25 s),当列车速度从30 km/h变化到60 km/h时,测点一在此阶段轴应力峰值由696.23 kN/m2变为912.34 kN/m2,增加约31%;测点二在此阶段轴应力峰值由615.84 kN/m2变为877.78 kN/m2,增加约42.5%。可见,轴重的改变对于整个列车行驶阶段最大峰值的影响是可忽略的,其影响主要在于轴重的增加在列车平稳形式阶段会相应增大架空结构各部件的所受轴力大小。但总的来说,当列车通过架空结构测点位置时,架空结构的拉、压应力远小于架空结构材料的强度限值,因此,该工况列车荷载作用下不会对架空结构安全性造成破坏。

3.3 现场监测对比

通过采集现场列车通过时测点的竖向振动加速度时程曲线,可以实时掌握架空体系动力响应,并根据现场情况及时采取安全防治措施[23-26]。本工程中,采用SDY400数据采集分析系统对5号箱涵顶进段进行动力监测,其监测系统包括含16个16位高精度AD采集通道的WS-U60116数据采集器,以及采用SD135-1内装集成电路的传感器,其低频特性优越,可做长期振动监测使用。顶进期间,应于图8所示测点,对5#箱涵顶进阶段进行了现场动力响应监测,分别对钢枕、架空桩以及横抬梁在列车动荷载下的加速度变化进行现场监测,以验证数值模拟的合理性,并给施工提供指导作用,监测流程如图15所示。

图15 监测流程图Fig.15 Monitoring steps

图16 钢枕测点一时程曲线对比Fig.16 Comparison of time history curves of steel sleeper measuring point 1

图17 钢枕测点二时程曲线对比Fig.17 Comparison of time history curves of steel sleeper measuring point 2

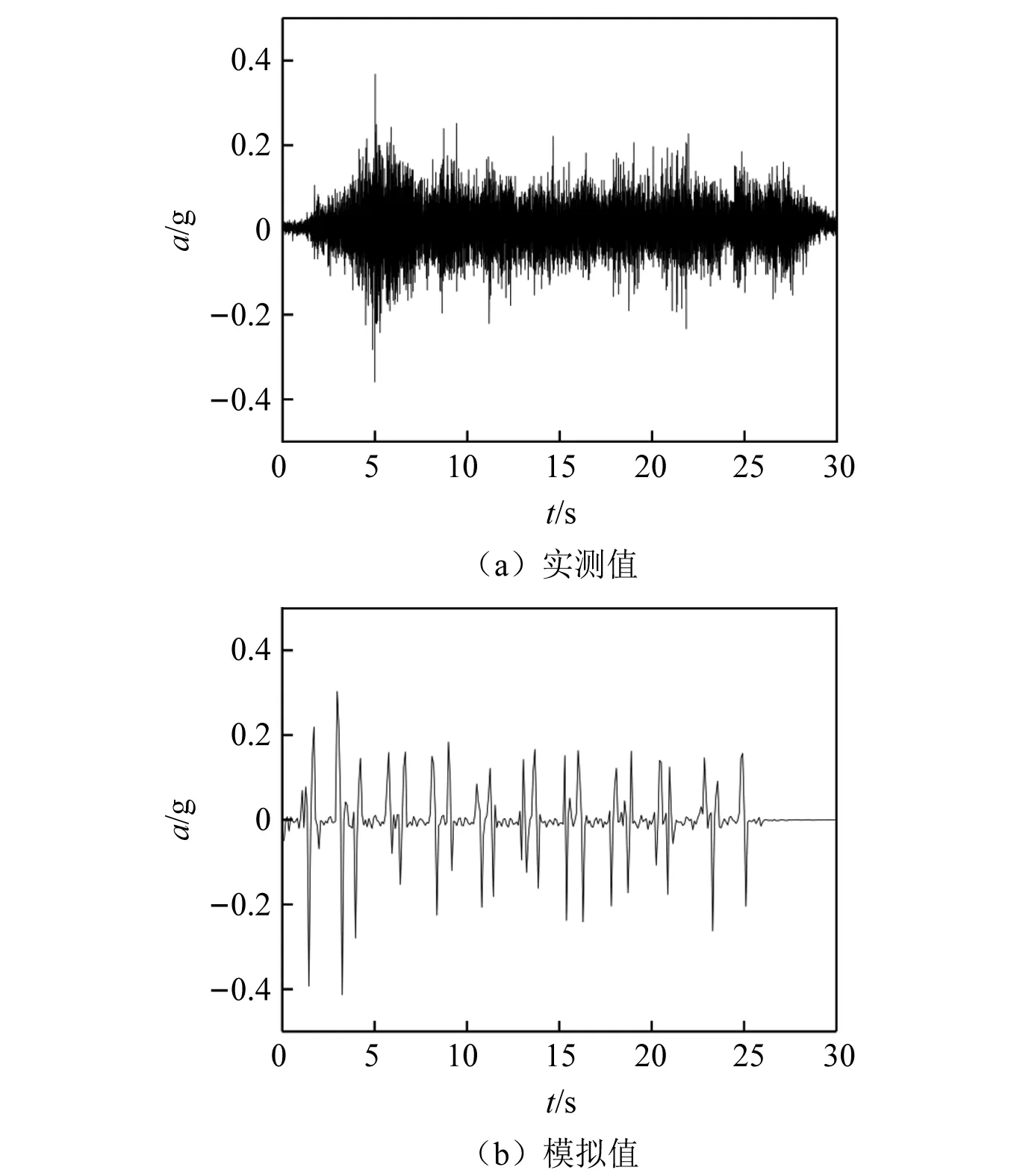
图18 架空桩测点时程曲线对比Fig.18 Comparison of time history curves of overhead pile measuring point

3.3.1 钢枕测点时程曲线对比

可以看出,对于测点一,实测数据显示其加速度最大值约1.62g,出现在第3 s。而数值模拟结果中,加速度最大值约1.74g,出现在第2 s。之后测点加速度变化幅值有所减小,而在20～25 s时加速度有所增加,最后随着列车的驶离,加速度减小到0。

对于测点二,实测数据显示其加速度最大值约1.33g,出现在第3 s。而数值模拟结果中,加速度最大值约1.32g,出现在第2 s。中间测点加速度变化幅值有所减小,而分别在第20 s和第25 s时,实测结果和数值结果有所增加,最后随着列车的驶离,加速度减小到0。

3.3.2 架空桩测点时程曲线对比

从架空桩测点时程曲线对比可知,实测加速度最大值约3.5g,出现在第5 s。数值结果中加速度最大值约4.1g,出现在第3 s。之后加速度幅值有所减小,并且实测数据在2.5g内波动,数值结果在2.2g内波动。最后分别在28 s和26 s后,两结果中加速度逐渐降低,直至为0。

从各测点实测结果和数值结果对比可以看出,与数值模拟相比,由于现场实测受到诸多环境因素的影响,比如施工中设备振动、千斤顶液压机振动、环境噪音等的存在都会对监测结果有所影响,相对来说数值模拟是理想型的,所以导致实测数据的变化频率高于数值模拟,这也导致了两者的频响差异。但数值模计算和实测数据所得的加速度峰值都在一个数量级,各测点实测数据和数值模拟结果不但在数值大小上接近,并且时程曲线规律基本相同,数值模拟结果在振动加速度响应规律上与现场实测规律吻合较好,由此可基本判断数值模拟在该方法下可较好模拟现场实际工况。

3.4 既有线架空结构体系的稳定性评价

由动力模型数值计算结果可知,在不同列车运行速度和列车轴重荷载作用下,各特征分析点的加速度、位移值及轴应力峰值均在容许范围内,即正常情况下施工结构是安全的。由计算结果可知,随着列车运行速度和列车轴重的增加,架空结构结构体系的动力响应越明显,同时考虑到既有线列车的运输能力和运输秩序,故将既有线客货运列车通过架空段时的运行速度限制在45 km/h,同时需对架空结构体系进行严格现场监测并加强施工控制,以免因响应超限造成上部铁路线路无法运营和后期施工的不便。

4 结 论

本研究基于经九路—陇海铁路立交工程5#箱涵顶进段架空工况,针对既有线架空体系的动力问题,采用数值模拟和现场测试方法,对两股道既有线上不同行车速度及不同轴重的列车作用下的铁路架空结构的动力响应规律进行了研究。主要的研究结论如下:

(1) 架空体系各部位在不同列车运行速度和列车荷载下的各动力响应,即振动加速度、竖向位移和轴应力响应时程曲线变化规律基本相同,主要都表现为列车驶入阶段动力响应急剧增大,列车平稳行驶阶段各动力响应曲线较为平稳,而在列车驶出远离阶段动力响应逐渐减小,并且各动力响应峰值主要出现在列车驶入阶段。

(2) 架空体系各部位的动力响应基本上都是随着列车车速的增大而增大,随着列车荷载的增大而增大,但相对而言,架空体系的动力响应对列车速度变化的敏感性要比对列车荷载的敏感性强。同时,相同条件下,架空桩动力响应对行车速度和行车荷载改变的敏感性要比钢枕强。所以,相比于行车荷载的改变,实际中应更多注意行车速度改变引起架空体系的动力响应的变化情况,且应将架空桩动力响应变化情况列为重点变化指标。

(3) 通过数值分析和现场实际监测数据分析可知,对于整个临时架空体系,各测点的加速度响应时程曲线规律基本相同,模拟结果和监测结果较为接近,同时各数值大小都在工程允许范围之内,架空体系较为稳定。