磁场中轴向运动铁磁梁固有振动与内共振的理论及数值模拟研究

崔 雪, 孔祥清, 胡宇达

(1.辽宁工业大学 土木建筑工程学院,辽宁 锦州 121000; 2.燕山大学 建筑工程与力学学院,河北 秦皇岛 066004)

轴向运动体系在工程实际中普遍存在,例如高速轴向运动的磁悬浮列车、空中缆车索道和电梯的牵引绳和动力传输带等等。轴向运动梁作为一种常见的结构,其横向振动和稳定性的研究在工程中有着重要的研究价值。Mote等[1-2]是最早研究轴向运动体系振动稳定性问题的国外学者。对于轴向运动梁,彭丽等[3-4]对轴向运动梁的非线性强迫振动、非线性动力学及稳定性等做了大量研究工作。丁虎等[5]总结了轴向运动梁做自由振动、受迫振动和参激振动时两组横向模型的解析解研究进展。文献[6]研究了轴向运动梁的横向耦合振动的非线性问题。在磁弹性问题上,郑晓静等[7-8]对铁磁材料在电磁场作用下的弯曲、失稳等问题进行了深入的研究,给出了基本的理论框架和计算方法。周纪卿[9]给出了无轴向运动的梁在磁场中的振动方程,并进一步研究了梁的稳定性问题。胡宇达等[10-12]研究了磁场中导电梁和导电薄板的非线性共振、参数振动及动力稳定性等问题。文献[13]通过复模态方法求解了3种模型的控制方程,给出了其相应的固有频率及模态函数。Li等[14]研究了内共振条件下四边简支边界条件下的矩形板全局分岔和多脉冲动力学问题。胡海良等[15]利用改进的摄动法研究了含有立方项和平方项的非线性系统的1 ∶3内共振问题。黄玲璐等[16]用直接多尺度法研究了轴向运动梁的内共振问题。

目前,针对磁场环境下轴向运动体系的研究还较少,本文针对电磁力激发下铁磁梁的双向耦合振动问题进行研究,并考虑其轴向运动条件,解出梁双向固有振动的固有频率表达式。并进一步研究系统发生内共振时梁的振动特性。最后通过有限元方法得到了和理论解比较吻合的数值解。本文研究结果可以为后续研究梁的受迫振动提供理论基础。

1 磁场中轴向运动铁磁梁的非线性振动方程

研究图1所示在恒定横向磁场B0(0,By,0)中做轴向运动的铁磁梁,设梁的弹性模量、密度和电导率分别为E,ρ和σ,轴向拉力为T0x,梁横截面为矩形,高为h,宽度为b,沿着x方向的轴向运动速度为c。

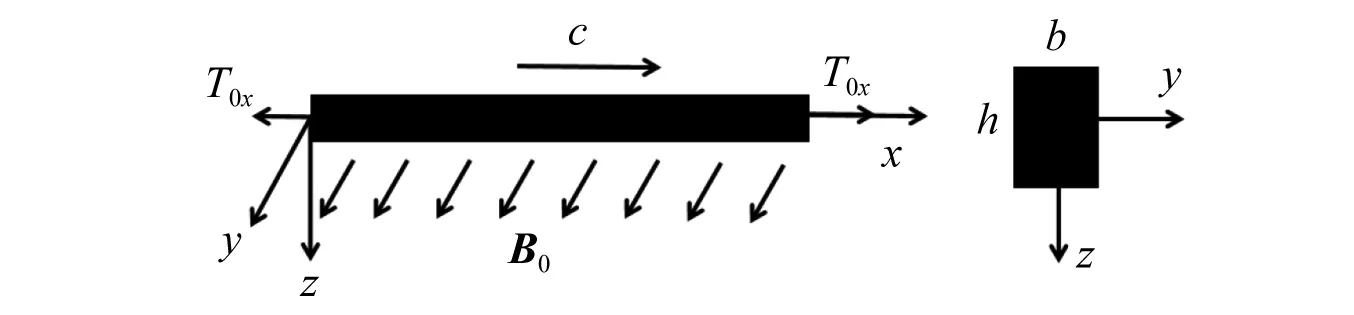
图1 轴向运动铁磁梁模型Fig.1 The model of ferromagnetic beam model with axially moving

1.1 洛伦兹力

当铁磁梁在磁场中轴向运动时,由电磁场理论可知,由于振动时切割磁感线使梁内产生感应电流,其电流密度为

(1)

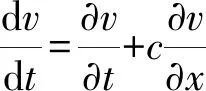
由式(1)可得洛伦兹力矢量表达式为

(2)

从而可以得到磁场中铁磁梁所受单位长度横向电磁力为

(3)

1.2 磁体力偶

因为梁的变形将导致梁内磁场发生变化,设梁内总磁感应强度为

B=B0+θ(t)B1

(4)

式中:B为梁变形引起的摄动磁场;θ(t)为与时间有关的小的摄动参数。在梁的正弦变形形式下[17]有

B=χmByΔ-1[coshkycoskx·i+sinhkysinkx·j]

(5)

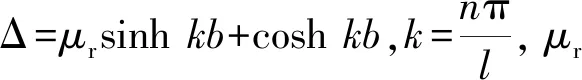
铁磁材料梁的磁化强度为

(6)

式中:μ0=4π×10-7为真空磁导率,H/m。

单位长度梁上作用的磁体力偶为

(7)

又在小变形下,设单位长度梁上受到的体积力偶与梁的挠曲线斜率成正比,则有

(8)

式中,k0为磁扭转刚度。由式(7)和式(8)可得

(9)

忽略x方向轴向振动,当轴向运动梁发生横向振动时,其动能为

(10)

根据弹性变形理论,可以得到梁的总势能表达式

U=U1+U2+U3

(11)

其中

式中:U1为梁的拉力引起的应变势能;U2为梁的中面应变势能;U3弯曲应变势能。

1.3 磁弹性双向振动方程

根据哈密顿变分原理得到在横向磁场中轴向运动铁磁梁的双向磁弹性自由振动方程为

(12)

(13)

式中,Iz和Iy分别为梁对轴z和y轴的惯性矩。

2 双向耦合固有振动问题理论求解

2.1 伽辽金法分离时间和空间变量

梁的边界条件为

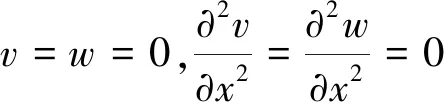
(14)

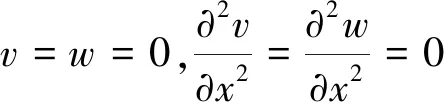
(15)

设满足边界条件的位移解为

(16)

(17)

将式(16)、式(17)代入式(12)、式(13),可得到分离时间和空间变量的梁的磁弹性双向耦合振动方程

(18)

(19)

式中:

2.2 求解耦合方程固有频率

利用多尺度法近似求解弱非线性方程式(18)、式(19)时,在方程组等号右端引入小参数ε,并改成如下形式

(20)

(21)

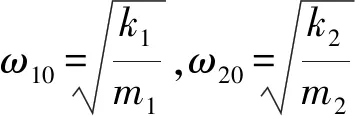
设系统的运动按不同时间尺度T0=t和T1=εt变化。将式(20)、式(21)的解写为

q1=q11(T0,T1)+εq12(T0,T1)

(22)

q2=q21(T0,T1)+εq22(T0,T1)

(23)

将式(22)、式(23)代入(20)、式(21),令ε的同次幂系数相等,得到一次近似方程

(24)

(25)

二次近似方程

(26)

(27)

设式(26)、式(27)的复数形式的解为

(28)

(29)

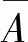
将式(28)、式(29)代入式(26)、式(27)得到

(30)

(31)

式中,cc为等式右侧各项的共轭。

消除式(30)、式(31)长期项的条件是

(32)

(33)

将复函数A1,A2对t的导数写为

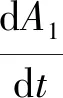
(34)

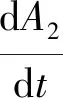
(35)

式中:D0A1=0;D0A2=0;D1A1和D1A2由式(32)、式(33)确定。

联立式(32)～式(35),得到

(36)

(37)

设复函数Ar写成如下指数形式

(38)

式中,ar(T1),βr(T1)均为T1的实函数。

将式(38)代入式(36)、式(37),分离实部和虚部得到

(39)

(40)

(41)

(42)

积分式(39)和(40)得到

a1=a01

(43)

(44)

式中,积分常数a01和a02取决于初始条件。

所以得到系统固有振动频率为

y方向

(45)

z方向

(46)

2.3 内共振情况

观察式(32)、式(33)可知,当派生系统的两个固有频率满足1∶1时,系统将发生内共振。

设派生系统的两个固有频率满足

ω10=ω20+ελ

(47)

式中,λ为引入的频率调谐参数。

考察式(30)、式(31)发现,除了正比于eiω10T0和eiω20T0的项外,式中正比于ei(ω10-2ω20)T0和ei(2ω10-ω20)T0项也会产生长期项。

这时消除式(30)、式(31)长期项的条件是

(48)

(49)

将式(38)代入式(48)、式(49),将实部和虚部分离得到关于a1,a2,β1和β2的常微分方程组

(50)

(51)

(52)

(53)

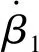
(54)

3 算例分析

3.1 非内共振

对横向磁场中轴向运动铁磁材料梁的固有振动特性进行分析。梁的物理参数如表1所示。梁材料选择纯铁,梁横截面面积为A=b×h=0.02 m×0.03 m,长度为l=1 m。

表1 纯铁的物理参数

图2和图3分别给出了梁在y方向和z方向振动的固有频率ω1和ω2随时间的变化曲线。在振动的初始阶段,固有频率ω1和ω2随时间减小,最终趋于一个常值。对比图2(a)和图3(a),图2(a)中3条曲线没有重合,是由于式(45)中存在磁扭转刚度k0。由此可知当时间足够大时,固有频率ω1与磁场强度有关,而ω2与磁场强度无关。由图2(b)、图2(c)和图3(b)、图3(c)相比较可以看出:当时间足够大时,初始振幅a01不同,对应的固有频率ω1和ω2也不同;初始振幅a02不会影响固有频率ω1和ω2。

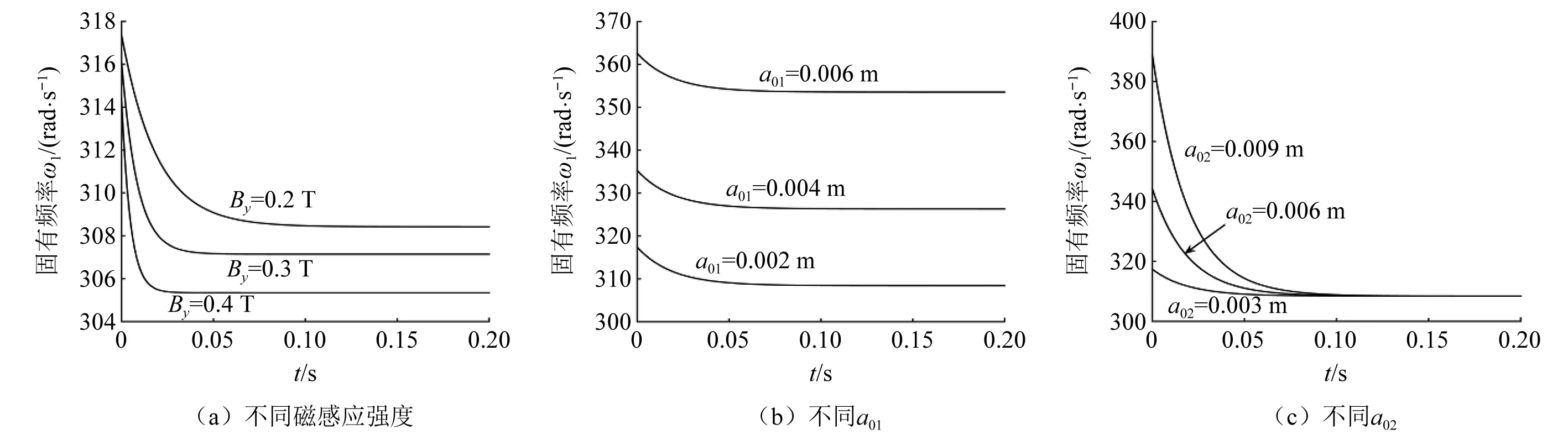
图2 ω1随时间变化规律Fig.2 Variation of ω1 with time

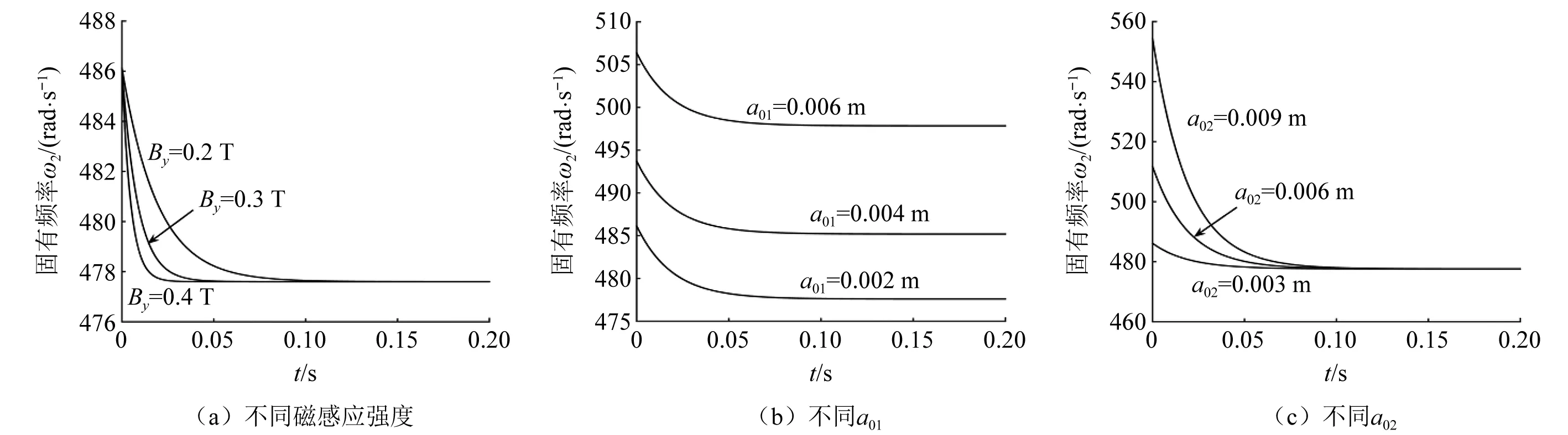
图3 ω2随时间变化规律Fig.3 Variation of ω2 with time

图4和图5分别给出了磁感应强度和轴向速度对固有频率ω1的影响曲线图。图6和图7分别给出了磁感应强度和轴向速度对固有频率ω2的影响曲线图。从图中可以看出固有频率ω1和ω2都随着磁感应强度和轴向速度的增大而减小。图4(c)中当磁感应强度达到某一值后3条曲线重合,是因为当磁感应强度较小时,初始振幅a02对ω1有较大影响,而当磁感应强度大于某一个数值时,初始振幅a02对ω1基本没有影响。图5(a)和图7(a)中曲线较密集,说明磁感应强度对ω1和ω2的影响较小。图6中3条曲线随磁感应强度增大而逐渐平行y轴,表明当磁感应强度足够大时,其对ω2的影响会显著降低。图6(c)中当磁感应强度达到某一值后3条曲线相交,表明当磁感应强度足够大时,ω2的大小与a02无关。

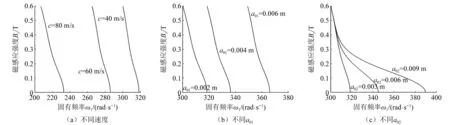
图4 By与ω1之间的关系Fig.4 Relationship between By and ω1

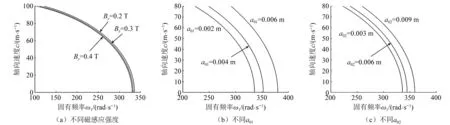
图5 c与ω1之间的关系Fig.5 Relationship between c and ω1

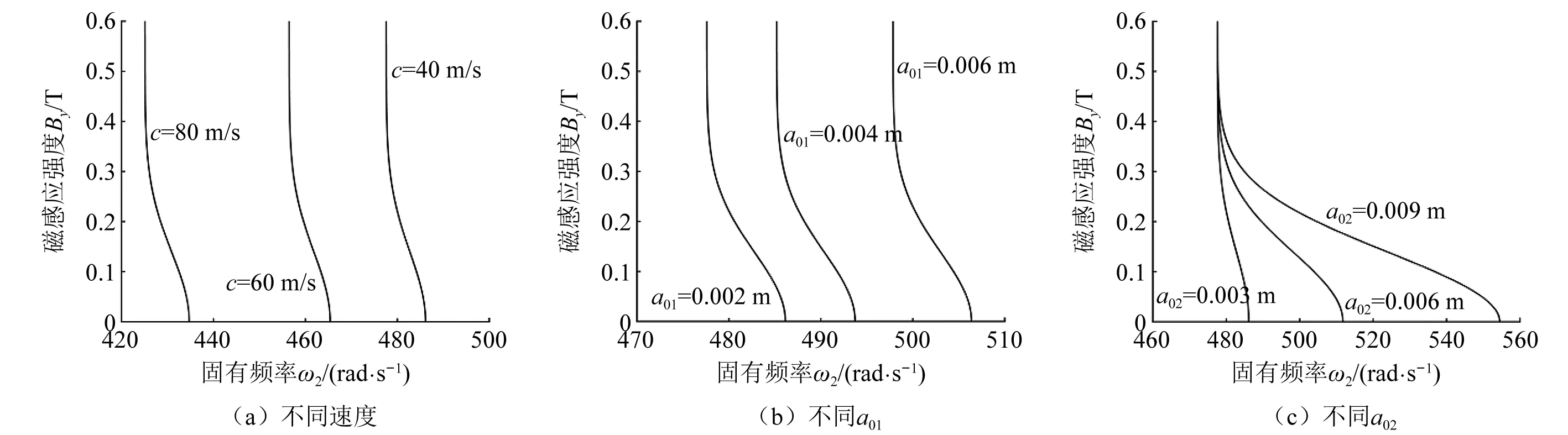
图6 By与ω2之间的关系Fig.6 Relationship between By and ω2

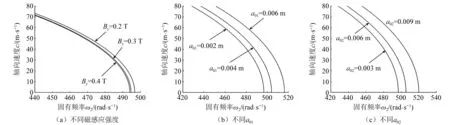
图7 c与ω2之间的关系Fig.7 Relationship between c and ω2

3.2 内共振

对横向磁场中轴向运动纯铁材料梁的内共振特性进行分析。梁物理参数见表1。

当梁发生1 ∶1内共振时,由固有频率表达式可知,当梁长和宽越接近相等,两个方向振动固有频率越接近1 ∶1,故选择梁横截面面积A=b×h=0.03 m×0.03 m。

图8～图12给出了系统发生内共振时振幅a1和a2随时间变化的曲线图。图(b)是图(a)在时间段0～0.001 s的截图,图(c)是图(a)在时间段0.05～0.051 s的截图。从图中可以看到系统的能量在a1和a2之间不断的交换,发生了明显的内共振现象。对比图8～图10可以看出,当轴向速度为40 m/s,60 m/s和80 m/s时,局部放大图变化微小,可知轴向速度对系统内共振影响较小。对比图8、图11和图12可以看出,当磁感应强度为0.2 T,0.3 T和0.4 T时,局部放大图变化明显,可知磁感应强度对系统内共振影响显著,且磁感应强度越大,系统内共振现象越不明显。

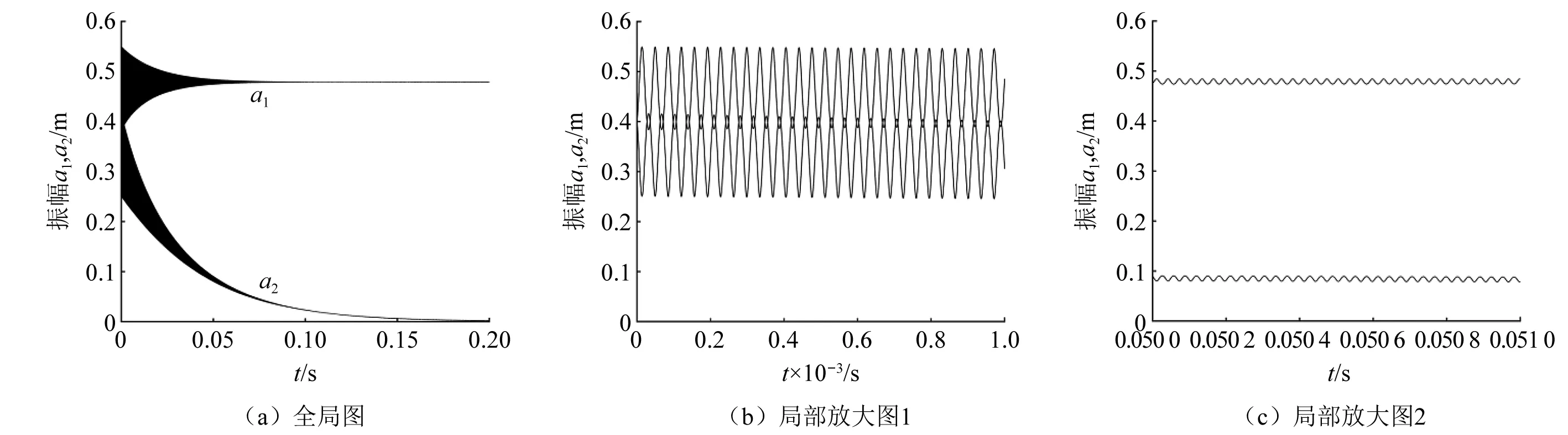
图8 振幅能量交换时程图(By=0.2 T, c=40 m/s)Fig.8 Amplitude energy exchange time histogram (By=0.2 T, c=40 m/s)

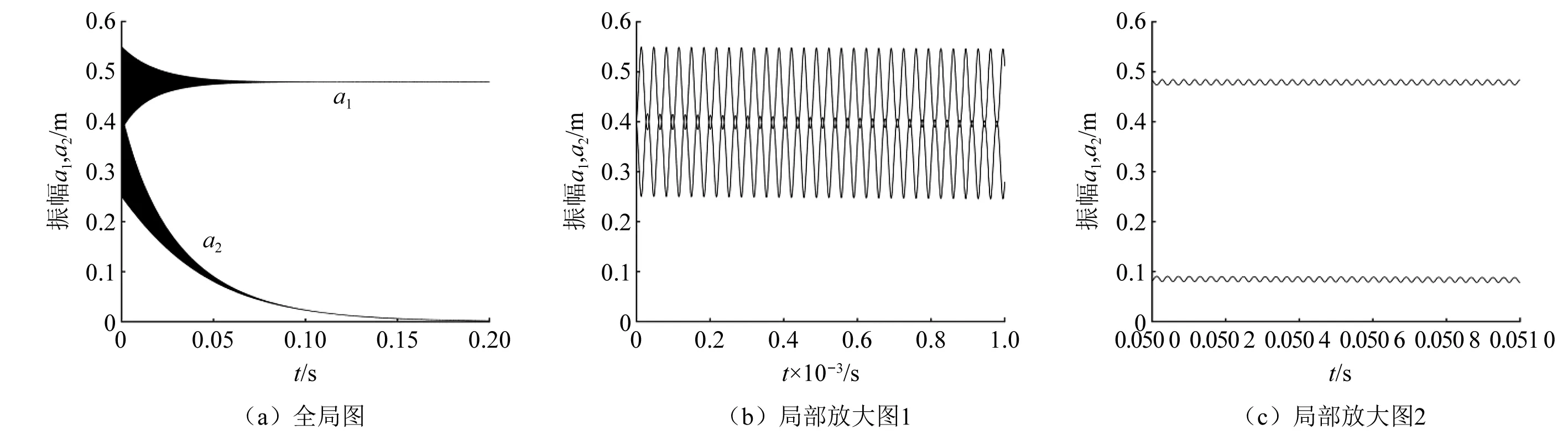
图9 振幅能量交换时程图(By=0.2 T, c=60 m/s)Fig.9 Amplitude energy exchange time histogram (By=0.2 T, c=60 m/s)

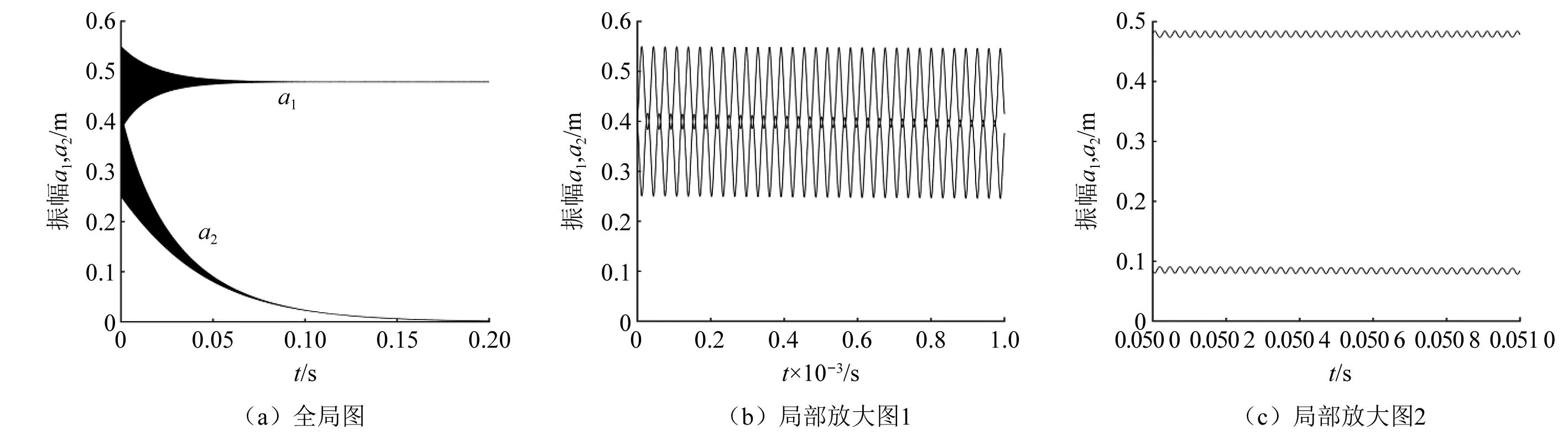
图10 振幅能量交换时程图(By=0.2 T, c=80 m/s)Fig.10 Amplitude energy exchange time histogram (By=0.2 T, c=80 m/s)

图11 振幅能量交换时程图(By=0.3 T, c=40 m/s)Fig.11 Amplitude energy exchange time histogram (By=0.3 T, c=40 m/s)

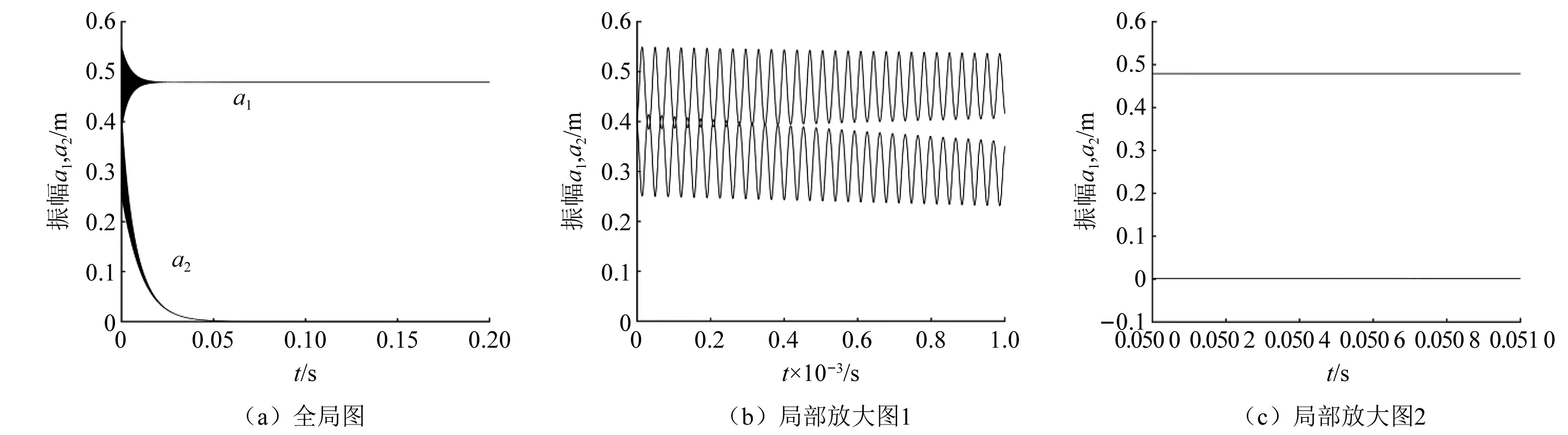
图12 振幅能量交换时程图(By=0.4 T, c=40 m/s)Fig.12 Amplitude energy exchange time histogram (By=0.4 T, c=40 m/s)

图13 梁振动的前12阶模态Fig.13 First twelve modes of beam vibration

4 有限元分析

4.1 计算模态和固有频率

利用ABAQUS有限元软件软件建立了梁的三维实体模型,将梁划分为10 000个单元,单元类型为C3D8R。计算了梁振动的前12阶模态,并求解出各阶模态对应的振动频率。

由图(13)可知梁的前9阶振动模态均为y方向和z方向的振动,第10阶模态为沿着轴向的振动,第11阶模态为沿着轴向的扭转,第12阶模态又回到了y方向。图14给出了各阶模态对应的固有频率。

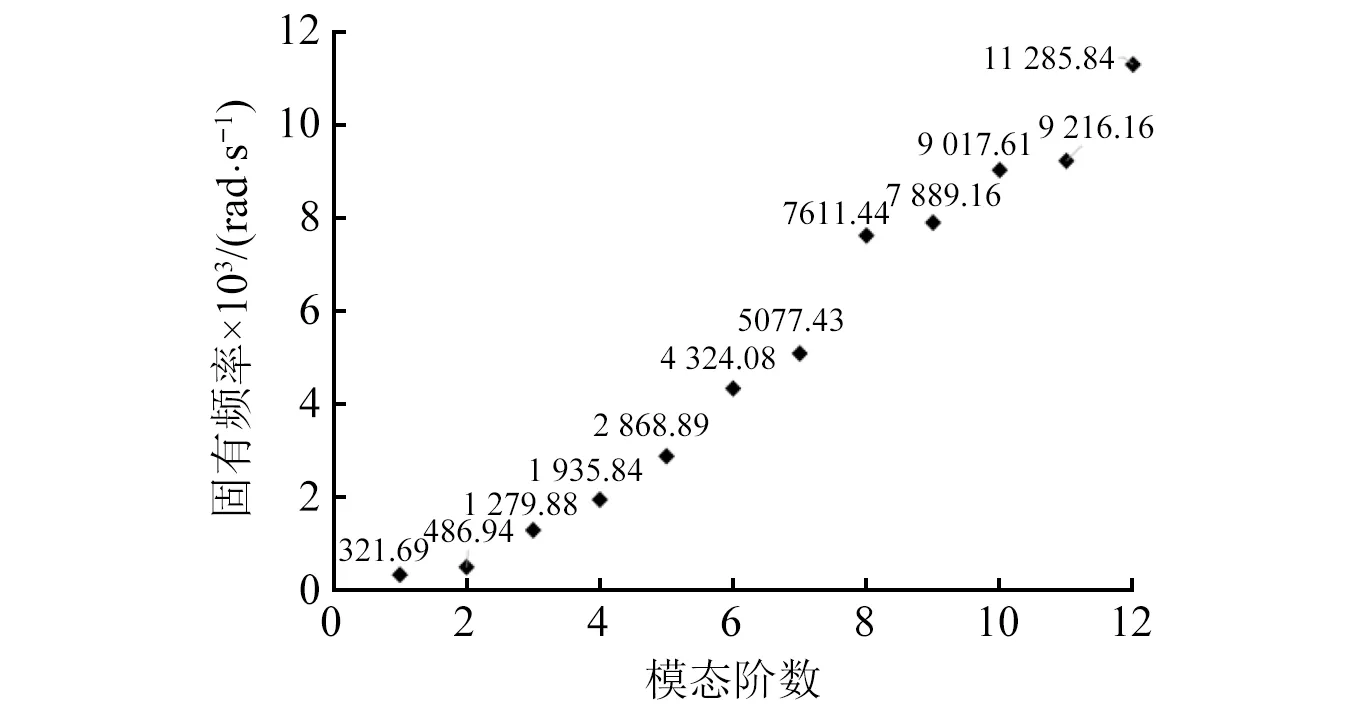
图14 各阶模态对应的固有频率Fig.14 Natural frequencies corresponding to each mode

4.2 理论解与数值模拟对比

表2给出了梁振动固有频率的理论解和数值解,的理论解为342.21 rad/s,数值解为321.69 rad/s,误差为6.00%;ω2的理论解为501.11 rad/s,数值解为486.94 rad/s,误差为2.83%。

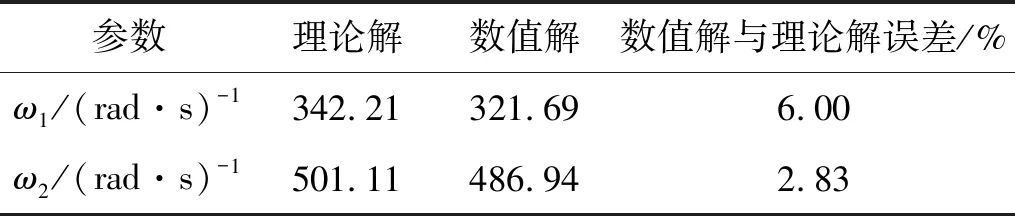
表2 固有频率理论解与数值模拟结果

经对比可知,理论求解和有限元分析结果吻合较好。

5 结 论

本文研究了横向磁场中做轴向运动铁磁梁的双向耦合固有振动和内共振,给出了洛伦兹力和磁体力偶表达式,利用哈密顿原理推导出了梁的振动方程,进一步研究梁1 ∶1内共振问题,并将理论解与数值解进行对比。本文得到结论如下:

(1)推导出了磁场中做轴向运动铁磁梁的非线性双向耦合振动方程以及梁在y方向和z方向振动固有频率的表达式。

(2)由固有频率表达式(45)、式(46)可知,当梁长和宽越接近相等时,系统将发生1 ∶1内共振,求解了系统内共振情况下的振幅和相位调制方程。

(3)梁固有频率随磁感应强度和轴向速度的增大而减小,最终趋于一个常值。

(4)y方向和z方向振动的固有频率数值解与理论解误差分别为6.00%和2.83%,两者吻合较好。