基于变论域模糊控制的时变结构震动控制方法研究

2023-10-10梅品彬李芳芳

振动与冲击 2023年18期

梅品彬, 李芳芳, 吕杨

(天津城建大学天津市土木建筑结构防护与加固重点实验室,天津 300384)

震动控制主要分为被动、主动、半主动及混合控制4类[1],其中半主动控制由于其耗能低、鲁棒性高、刚度可调等优点,得到国内外学者的广泛研究,已成功研制出节流式变阻尼控制装置、电/磁流变阻尼器、半主动调谐式质量阻尼器和半主动调谐式U型液体阻尼器等半主动控制装置[2],并在实际工程应用中取得了良好的控制效果。近年来,磁流变弹性体(magnetorheological elastomer, MRE)为半主动控制装置提供了一个新的选择。磁流变弹性体可根据外加磁场实时改变材料的剪切刚度[3],由磁流变弹性体制作的隔震支座可同时具备水平刚度可调、高竖向承载力等优点,已成为结构震动半主动控制发展的重要方向。

在基于磁流变弹性体支座的半主动控制算法方面,与磁流变阻尼器类似,较为常见的有线性二次型调节器(linear quadratic regulator, LQR)[4-5],H∞控制[6]、滑模控制[7]等,但上述控制算法较大程度依赖于被控结构的数学模型。针对传统控制算法的缺点,研究人员开发出了一系列不需要精确数学模型的智能控制算法,如模糊控制、神经网络等智能控制算法。邱志成等[8]采用神经网络控制器,长短期记忆网络作为预测网络,反向传播网络作为控制网络,通过仿真与试验验证了神经网络控制器能有效抑制结构振动响应;马天兵等[9]提出了一种改进滑模变结构控制算法,仿真与试验结果表明,该控制算法能较好地抑制加筋板的振动,且控制效果优于传统滑模控制;石运东等[10]提出一种地震动主频相关的加速度阈值变阻尼半主动控制方法,有限元模拟结果表明,该控制算法有效控制了三维隔震单层球面网壳结构节点加速度以及杆件轴力;郭佳等[11]将磁流变阻尼器模态模糊控制算法引入一个20层多自由度结构体系模型,控制后的结构层间位移和楼层速度得到有效减小;马驰骋等[12]提出一种模糊PID(proportion integration differentiation)控制器,仿真结果表明该控制器有效抑制了含变质量单元的柔性梁结构的振动响应;金耀等[13]提出一种新型复合结构的内分泌LQR控制器,应用于汽车主动悬架减振控制,研究结果表明内分泌LQR控制品质优良、对变化的工况参数具较好的适应性,减振效果要优于传统LQR控制;马天兵等[14]采用饱和补偿控制器对壁板结构进行振动控制,仿真及试验结果表明,该方法在多模态正弦复合随机扰动下,较EMCS(extended minimal control synthesis)算法鲁棒稳定性更好;王文等[15]采用MBC(market-based control)算法进行了模型结构振动控制试验研究,试验结果表明,MBC算法应用于实际结构中具有较好的减振控制效果。前述提出的控制方法一般均假定被控结构为定常系统,即结构质量和刚度等参数不随时间改变,但实际建筑结构均为时变系统,结构刚度和质量会随使用年限或地震过程发生改变,此时以初始结构特性设计的控制系统控制效果将发生变化[16]。模糊控制在处理时变系统的震动控制问题具有较大优势,但传统的模糊控制在设计模糊控制器前,需按照初始结构地震时的最大响应确定控制器输入、输出变量的量化因子、比例因子等模糊控制器参数,在结构特性发生变化时,模糊控制器的输入需求有可能超越模糊论域的情况,导致控制效果有所下降。

针对上述问题,本文在SIMULINK软件中建立一个考虑刚度退化及质量变化的三层框架结构,结构底层设置两个磁流变弹性体支座,将被控系统简化为一个四自由度体系模型,将变论域法引入模糊控制中,设计了地震前结构特性变化和地震过程结构特性线性降低两种工况,根据结构地震响应实时调整模糊论域,分析评价半主动变论域模糊控制对时变结构的控制效果。

1 变论域模糊控制器

1.1 控制器设计

针对传统模糊控制中模糊论域固定而导致控制效果下降这一问题[17],在模糊论域引入变论域思想,如图1所示。图1中:E为模糊控制器输入变量的论域边界;α为该输入变量的伸缩因子。

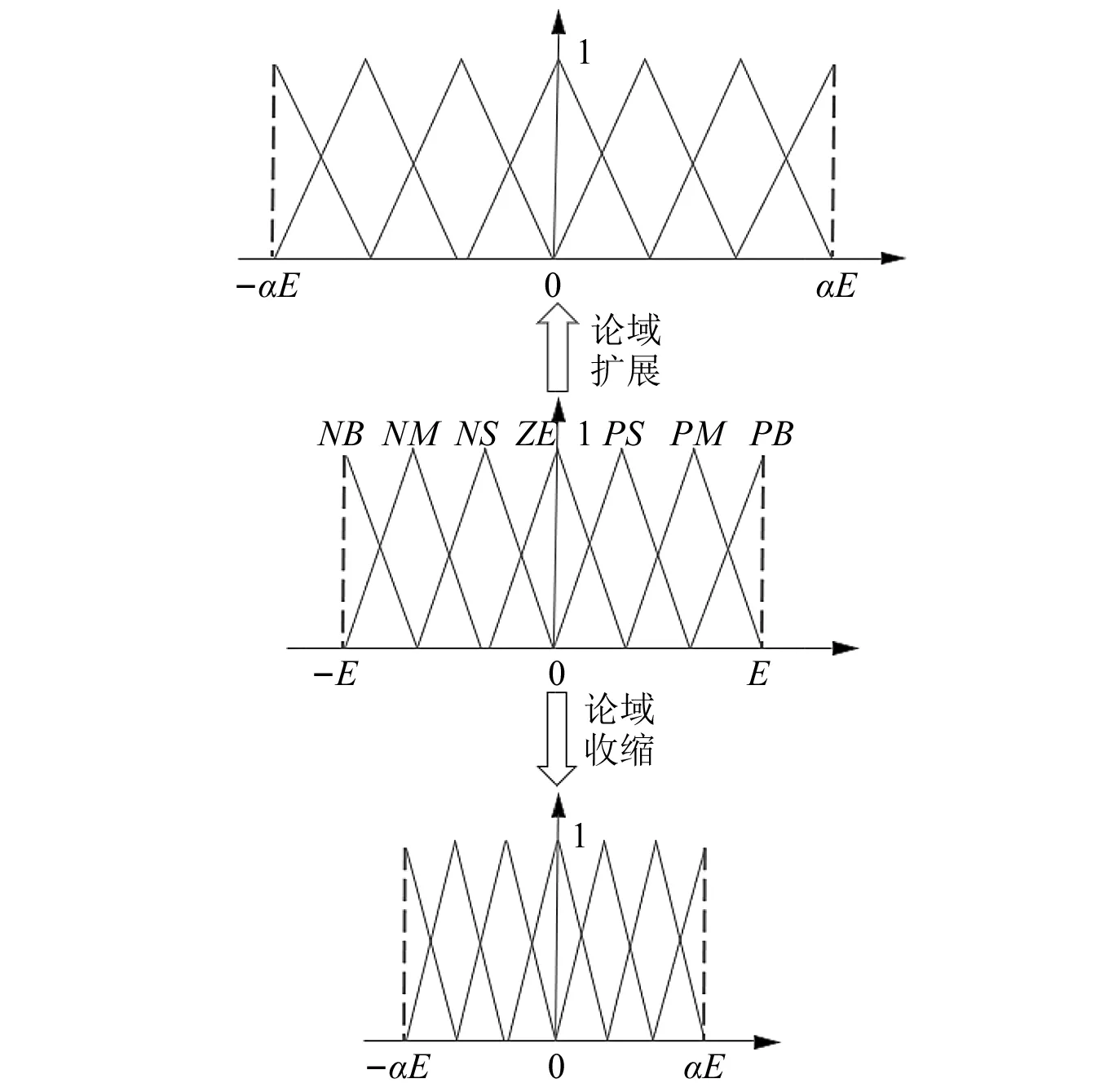
图1 变论域法基本原理Fig.1 Fundamentals of the variable domain method

设模糊控制第i个输入变量为误差ei(t),其模糊论域为Xi=[-Ei,Ei],其中:Ei为论域边界;α[ei(t)]为伸缩因子。当误差ei(t)增大时,适当提高伸缩因子α[ei(t)]的参数值,从而达到扩大模糊论域提高控制效果的目的。反之,当误差ei(t)减小时,适当降低伸缩因子α[ei(t)]的参数值。以两输入一输出的模糊控制为例,调整后的模糊论域为

(1)

式中:Xi(i=1, 2)为第i个输入变量的模糊论域;Y为输出变量的模糊论域;α[ei(t)](i=1, 2)为第i个输入变量的伸缩因子;β[u(t)]为输出变量的伸缩因子;Ei(i=1, 2)为第i个输入变量的论域边界;U为输出变量的论域边界。变论域模糊控制的具体计算流程如图2所示。

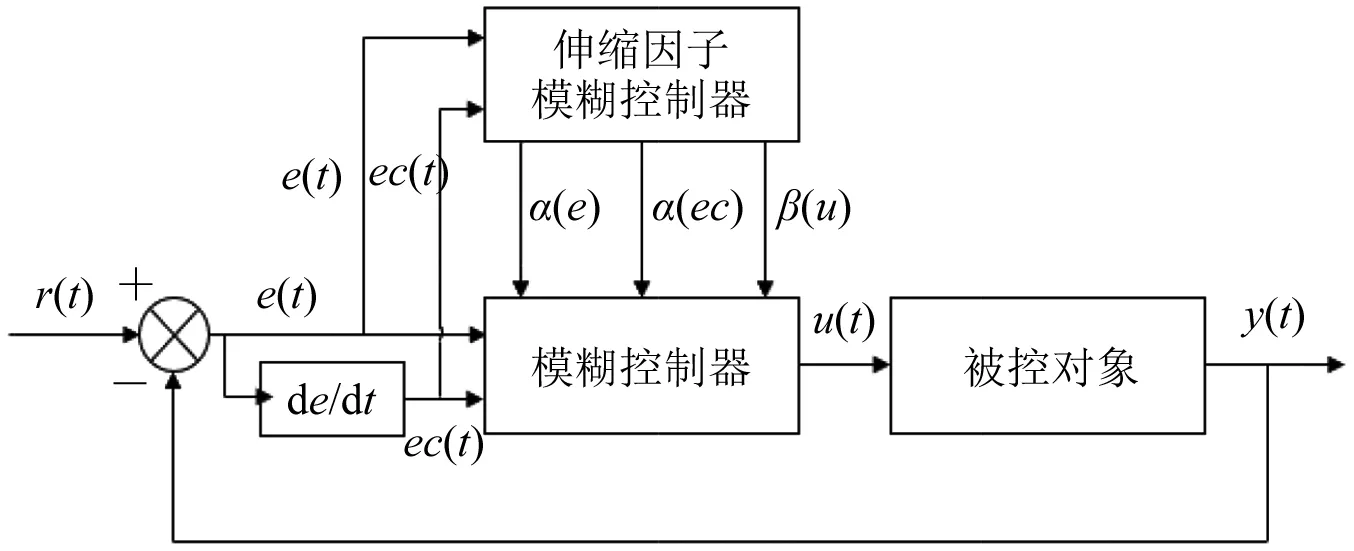
图2 变论域模糊控制流程图Fig.2 Variable domain fuzzy control flowchart

将基于模糊推理的伸缩因子模糊控制器与传统模糊控制器结合。其中,主模糊控制器的结构为两输入一输出,两个输入变量分别是结构响应误差e(t)=y(t)-r(t)及误差变化率ec(t),输出变量是磁流变弹性体支座的控制电流I(t);伸缩因子模糊控制器的输入变量与主模糊控制器一致,即以主模糊控制器e(t)和ec(t) 为输入变量,伸缩因子α[e(t)]和α[ec(t)]为输出变量;主模糊控制器输出变量I(t)的伸缩因子β[I(t)]设置为α[e(t)]和α[ec(t)]的线性组合,其表达式如下

(2)

式中,ε为一足够小的正数。

选取结构误差e(t)和误差变化率ec(t)的模糊论域为[-3,3];控制电流I(t)的模糊论域为[0,1];伸缩因子α[e(t)],α[ec(t)]的模糊论域为[0,1];量化因子、比例因子由结构初始状态下的响应确定。

将结构误差e(t)、误差变化率ec(t)和控制电流I(t)划分为7个等级,误差e(t)和误差变化率ec(t)使用模糊子集{NB,NM,NS,ZE,PS,PM,PB}表示;控制电流I(t)使用模糊子集{ZE,SM,S,M,SL,ML,L}表示;伸缩因子α[e(t)]和α[ec(t)]划分为4个等级,均使用模糊子集{ZE,S,M,L}表示。伸缩因子的控制规则如表1所示。

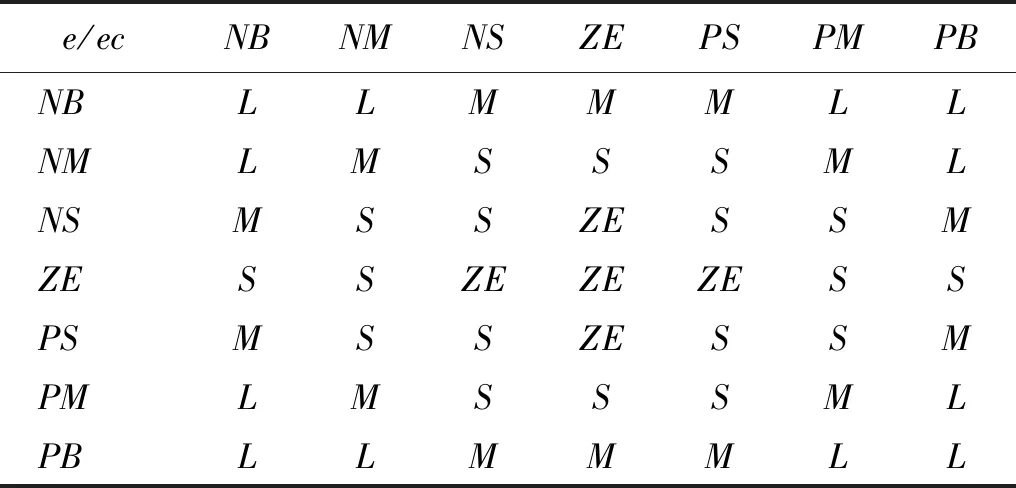
表1 伸缩因子α[e(t)],α[ec(t)]控制规则Tab.1 The scaling factor α[e(t)],α[ec(t)] control rules

变论域模糊控制器中输入输出隶属函数均采用三角形隶属度函数,利用最大隶属度法,对模糊量去模糊化,可得到论域调整后的磁流变弹性体支座控制电流I(t),需要说明的是,所有工况下控制电流不超过支座磁饱和电流。

1.2 控制装置

以磁流变弹性体支座作为控制装置,采用常见的Bouc-Wen模型描述MRE支座的力学性能[18]。Bouc-Wen模型结构如图3所示,其数学表达式如下

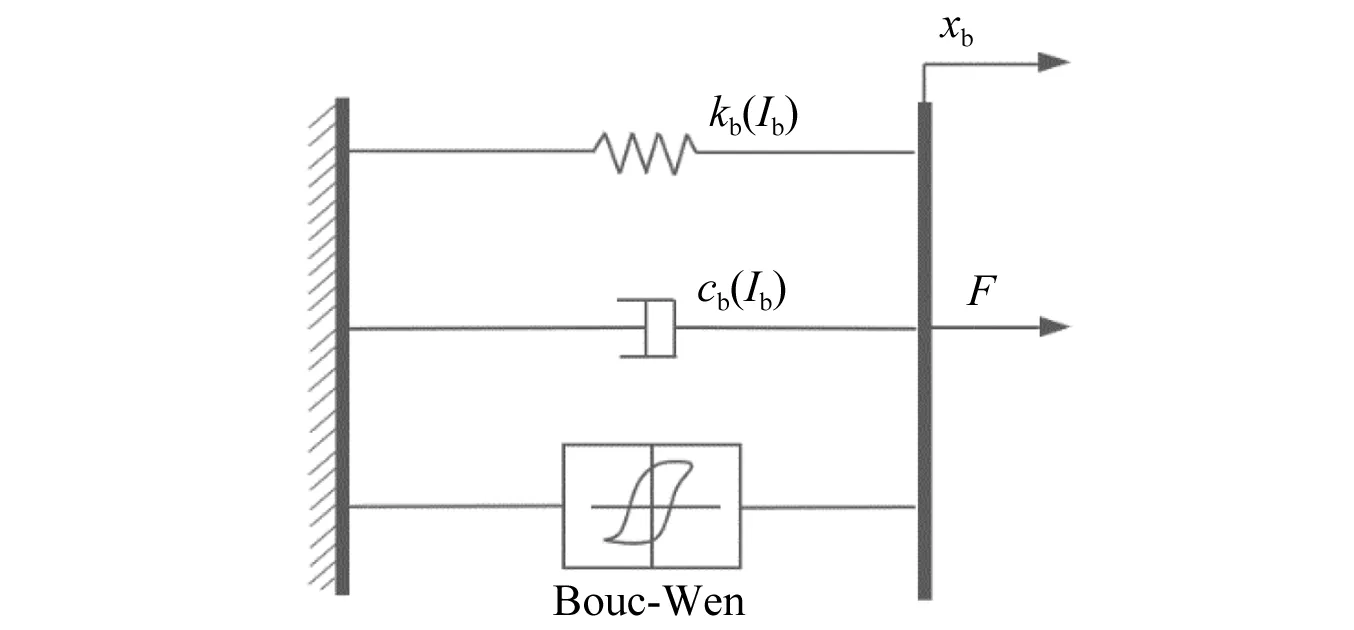
图3 Bouc-Wen模型示意图Fig.3 Schematic diagram of the Bouc-Wen model

(3)

式中:F为磁流变弹性体支座提供的剪切力;kb为支座的刚度系数;cb为支座的阻尼系数;α为屈服后与屈服前的刚度比;z为进化变量,描述了模型的滞回特性;A,β,γ为无量纲参数,决定滞回环的形状和大小;xb为支座的相对位移。

Bouc-Wen模型中待识别的参数共7个,分别为kb,cb,α,A,β,γ,n。文献[19]通过试验给出式(3)中系数kb,cb,α,A,β,γ与磁流变弹性体支座输入电流I符合以下关系

(4)

2 数值算例

2.1 结构参数

选取三层平面框架结构作为被控对象,下方设置两个磁流变弹性体支座,如图4所示。为提高控制效率,将系统简化为4自由度体系模型,楼板和支座质量集中于一点。采用瑞利阻尼,结构初始质量和刚度如表2所示。

表2 三层框架结构初始参数取值Tab.2 The initial parameters of the frame structure

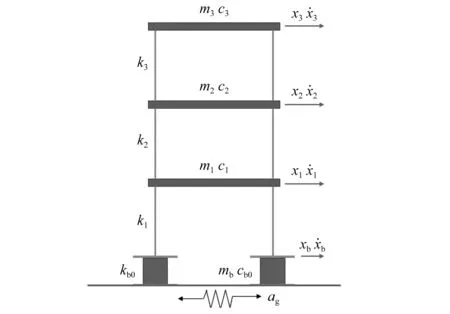
图4 三层框架结构布置简图Fig.4 Schematic diagram of the three-story frame structure layout

对该4自由度体系模型建立运动方程如下

(5)

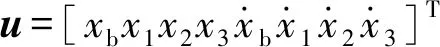
(6)

其中

(7)

(8)

(9)

2.2 时变结构控制器

采用SIMULINK仿真工具箱建立的时变结构控制系统如图5所示。选取峰值加速度为0.17g的El-Centro波南北向分量作为结构激励。以结构顶层位移x3作为控制器的输入,控制电流I(t)作为输出,考虑结构刚度退化、质量变化两种情况,对比分析无控、模糊控制、ON-OFF控制、变论域模糊控制下结构地震响应。其中,刚度变化考虑地震过程中结构各层刚度线性退化10%,15%,20%及地震发生前结构各层刚度退化10%,15%,20%,质量变化考虑地震过程中结构各层质量线性下降5%,10%,15%及地震发生前结构各层质量下降5%,10%,15%等工况。

图5 控制体系Fig.5 Control system

3 控制效果分析

3.1 结构刚度退化的影响

地震过程中发生刚度退化及地震前发生刚度退化时结构位移、速度和加速度均方根响应,如表3、表4所示。结果表明,结构顶层位移和速度均随着刚度退化率的增加而增加,减震率随着刚度退化率的增加而降低,但刚度退化率相同的情况下,变论域模糊控制的减震效果均优于模糊控制和ON-OFF控制。

表3 地震过程刚度退化结构响应评价指标Tab.3 Structural response evaluation index of stiffness degradation during earthquake

表4 地震前刚度退化结构响应评价指标Tab.4 Structural response evaluation index of stiffness degradation before earthquake

以地震过程中结构各层刚度线性退化20%和地震发生前结构各层刚度退化20%为例,不同控制算法的结构顶层位移时程曲线如图6和图7所示。由图6和图7可知,采用模糊控制的结构顶层位移均有一定幅度的下降,但在14～17 s,控制后的结构顶层位移出现放大现象,控制效果较差;变论域模糊控制则有效降低了时变结构顶层位移,所有时刻的控制效果均优于传统模糊控制和ON-OFF控制。

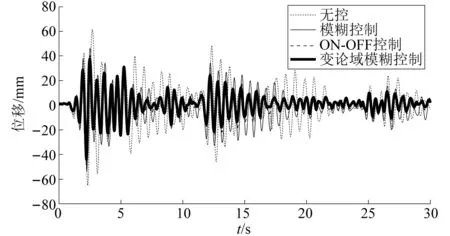
图6 地震过程中刚度退化20%顶层位移时程Fig.6 Comparison of the top displacement time histories considering 20% stiffness degradation during earthquake

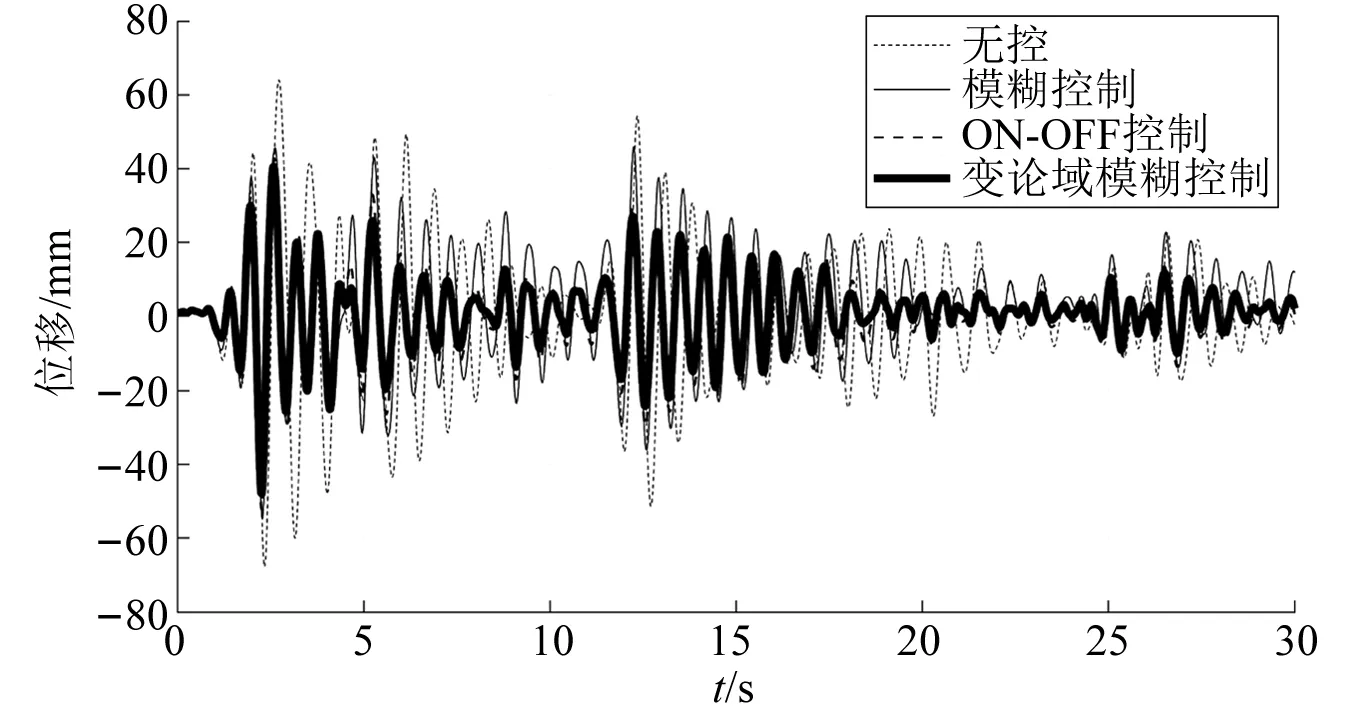
图7 地震前刚度退化20%顶层位移时程Fig.7 Comparison of the top displacement time histories considering 20% of the stiffness degradation before the earthquake

地震过程中结构刚度退化20%及地震发生前刚度退化20%情况下,采用不同控制算法的结构各楼层层间峰值位移,如图8、图9所示。由图8可知,当三层框架结构在地震过程中刚度线性退化20%时,无控状态下结构顶层峰值位移达65.10 mm,模糊控制、ON-OFF控制和变论域模糊控制下结构顶层峰值位移为53.91 mm,49.09 mm和44.25 mm,较无控工况分别下降了17.19%,24.59%和32.03%。由图9可知,三层框架结构在地震发生前刚度退化20%时,无控状态下结构顶层峰值位移为67.78 mm,模糊控制、ON-OFF控制和变论域模糊控制状态下结构顶层峰值位移为54.73 mm,52.36 mm和48.12 mm,分别降低了19.25%,22.75%和29.01%。

图8 地震过程中刚度退化20%时楼层层间峰值位移对比图Fig.8 Comparison of peak displacement between floors when stiffness degrades by 20% during earthquakes

图9 地震前刚度退化20%时楼层层间峰值位移对比图Fig.9 Comparison of peak displacement between floors when the stiffness degrades by 20% before the earthquake

3.2 结构质量变化的影响

地震过程中质量下降及地震前质量下降的结构地震响应,如表5、表6所示。结果表明,无控状态下结构响应随质量下降率增加而增大,采用变论域模糊控制器时,减震率随着质量下降率的增加而增大,且控制效果均优于其余两种控制算法。因此,变论域模糊控制能通过伸缩因子,根据结构响应,自适应调整模糊论域大小,从而实现结构响应增大时,适当扩大模糊论域,反之收缩模糊论域,实现更准确的震动控制。

表5 考虑地震过程质量下降结构响应评价指标Tab.5 Structural response evaluation index of quality degradation during the earthquake

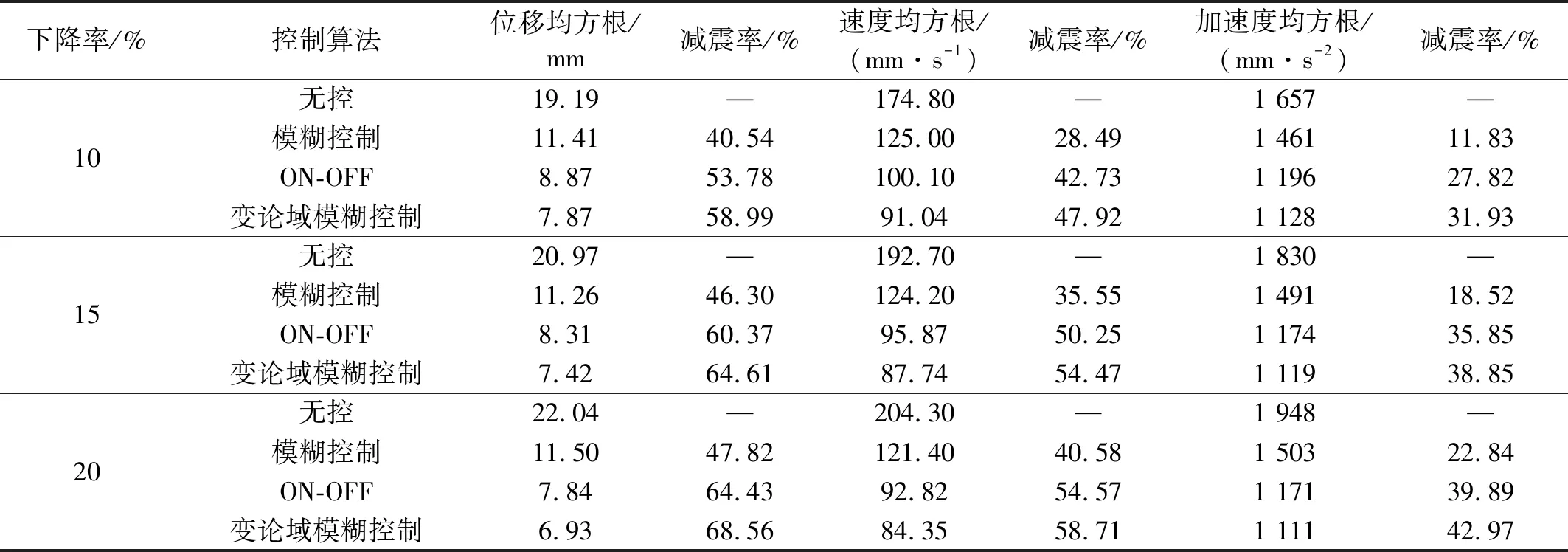
表6 考虑地震前质量下降结构响应评价指标Tab.6 Structural response evaluation index of quality degradation before the earthquake

以地震过程中结构各层质量下降15%和地震发生前结构各层质量下降15%为例,采用不同控制算法时结构顶层位移时程曲线,如图10和图11所示。由图10可知,模糊控制能在一定程度上减小结构顶层位移。各控制算法中,变论域模糊控制效果最优,其次为ON-OFF控制和模糊控制。由图11可知,3种控制算法均能有效降低结构顶层位移,其中变论域模糊控制效果最好。

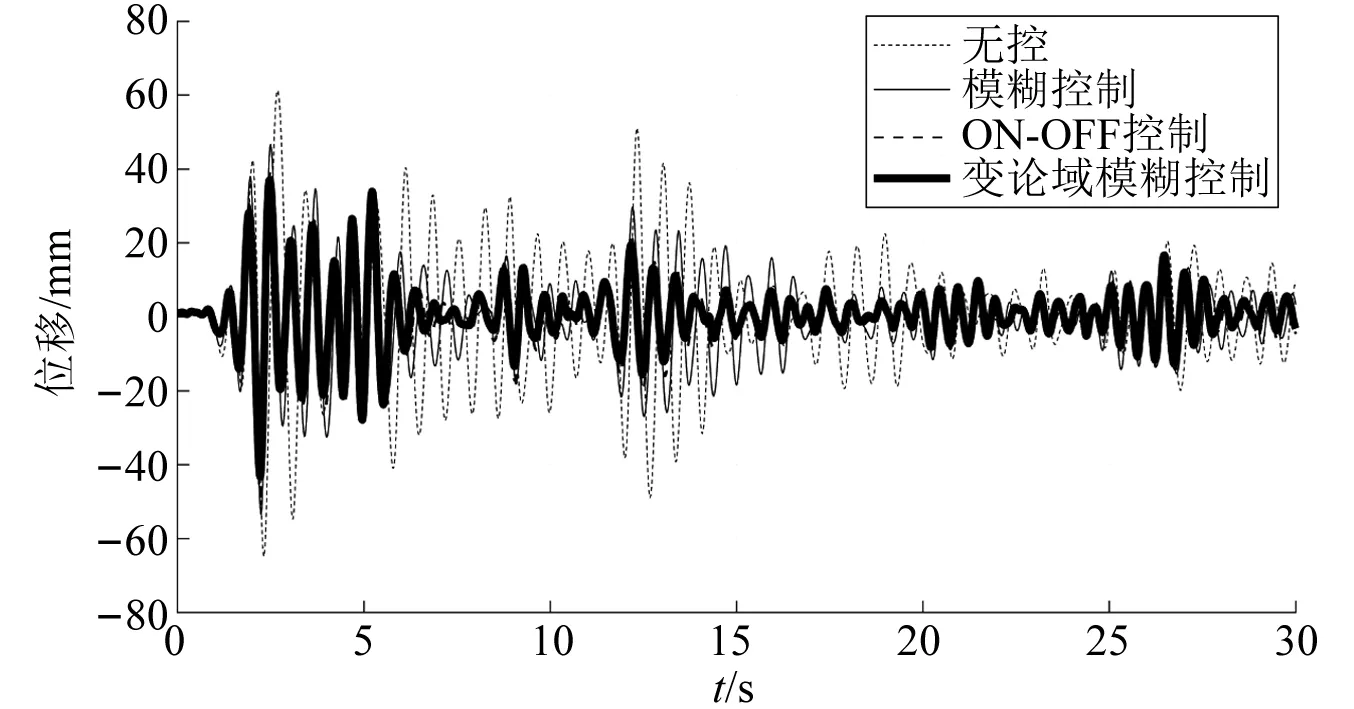
图10 地震过程中质量下降15%顶层位移时程曲线对比图Fig.10 Comparison of the top displacement time course curve of mass degradation by 15% during the earthquake

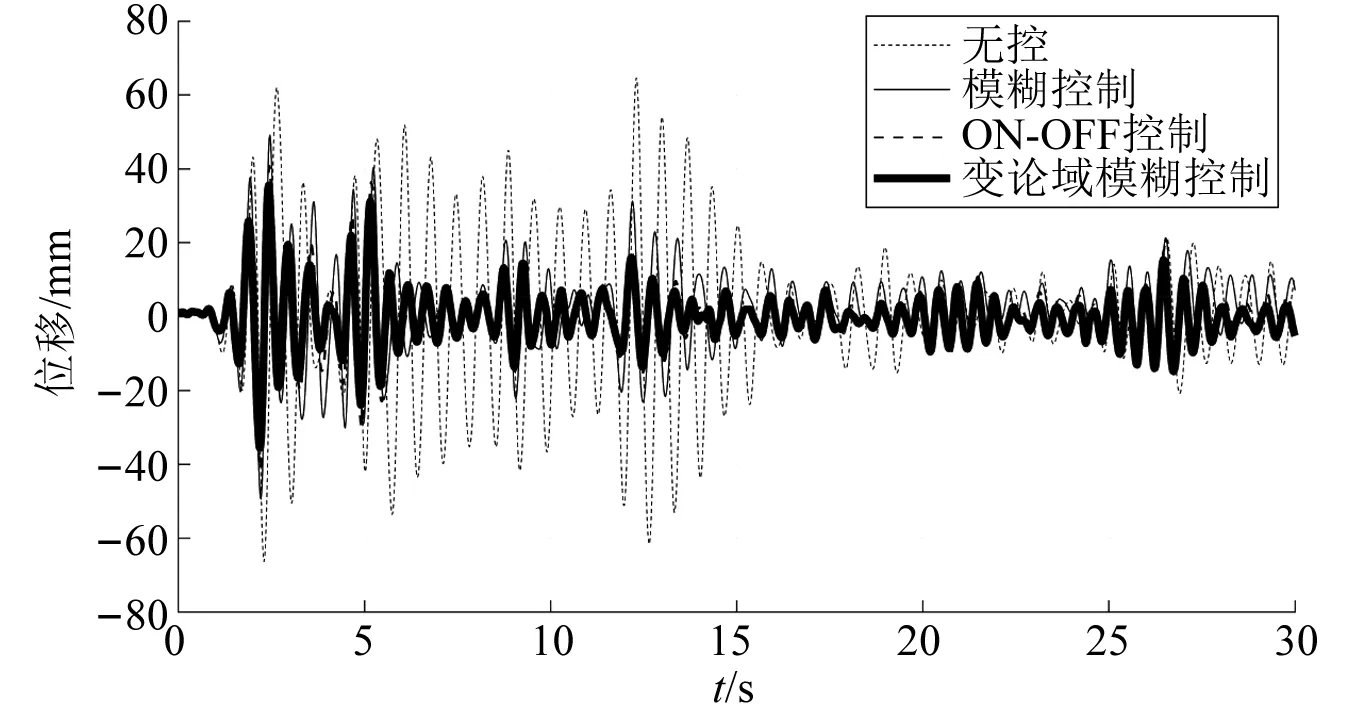
图11 地震发生前质量下降15%顶层位移时程曲线对比图Fig.11 Comparison of the top displacement time course curve of the mass drop of 15% before the earthquake

地震过程中结构质量线性下降15%和地震发生前质量下降15%情况下,采用不同控制算法的结构各层层间峰值位移,如图12和图13所示。由图12可知,当三层框架结构在地震过程中各层质量线性下降15%时,无控结构顶层峰值位移为64.84 mm,模糊控制、ON-OFF控制和变论域模糊控制下结构顶层峰值位移分别为53.48 mm,48.24 mm和43.33 mm,较无控状态分别下降了17.52%,25.60%和33.17%。由图13可知,当结构在地震发生前质量下降15%时,无控的结构顶层峰值位移为66.40 mm,模糊控制、ON-OFF控制和变论域模糊控制下结构顶层峰值位移分别为49.39 mm,41.52 mm和35.57 mm,分别降低了25.62%,37.47%和46.43%。

图12 地震过程中质量下降15%时楼层层间峰值位移对比图Fig.12 Comparison of peak displacement between floors during an earthquake when the mass drops by 15%

图13 地震发生前质量下降15%时楼层层间峰值位移对比图Fig.13 Comparison of peak displacement between floors when mass drops by 15% before the earthquake

地震过程中结构各层质量线性下降15%的情况下伸缩因子α[e(t)]的时程曲线,如图14所示。由图14可知,伸缩因子α[e(t)]在2.32 s左右时取得最大值10.23,这是由于El-Centro波在这个时间点附近达到峰值,系统响应误差增大,为达到减小结构响应的目的,控制器自适应提高了模糊论域。需要指出的是,为考虑磁流变弹性体支座磁饱和电流的限制,在所设计的控制器中设置了一个限值模块,使输出的电流始终保持在0～3 A内。变论域模糊控制能根据结构响应,自适应调整模糊论域大小,从而提高对时变结构的控制效果。