基于HFFB试验高耸结构风荷载谱高度修正系数及风振分析

楼文娟, 胡鹏瑞, 张跃龙

(浙江大学 结构工程研究所,杭州 310058)

实际工程中有很多高耸结构,风荷载是控制其设计的主要荷载。例如常在风灾中发生破坏的输电塔[1],使用在气象监测、广电发射等领域的格构式桅杆[2-3],在通信设施领域广泛应用的单管塔[4],此类结构外形细长,抗侧刚度小,对风荷载敏感。准确计算这些高耸结构的风荷载和结构响应十分重要。此类结构不便于开展测压试验,通过高频天平试验,可以获得更接近真实模式的结构响应和等效风荷载[5]。但天平试验只能获得结构基底的六分量风荷载谱,Tschanz等[6]指出对于线性振型结构,水平向风荷载的广义模态力与基底弯矩相等,因此高频天平(high-frequency force balance,HFFB)方法能够准确计算线性振型结构的模态响应。对于非线性振型结构,则需要对结构荷载分布作出假设。目前主要有3种非线性振型结构模态力计算方法,分别是振型修正系数法[7],层荷载假设法[8]和基底荷载谱分段估计法。分段估计法能较好的反映风荷载空间分布特性,在实际工程中应用普遍,它通过估算高耸结构脉动风荷载的空间分布,将基底荷载谱向上部结构分配从而得到各节点风荷载谱。肖正直等[9-10]在脉动风荷载准定常假定的基础上提出基底荷载谱的分段估计法,用于估算脉动风荷载的空间分布。肖正值等[11]还对某特高压直流输电塔进行了天平测力试验和气弹模型试验,使用分段估计法对输电塔进行风致响应分析,并与气弹模型风洞试验结果对比,结果表明分段估计法能较好地体现结构的非线性振型特性。黄俏俏[12]基于HFFB试验采用分段估计法得到了各节点的风荷载互功率谱,计算塔架风致响应,并与线性振型假定下的计算结果进行对比。

分段估计法假设风荷载无量纲自功率谱沿结构高度不变,依据准定常假定推算结构各高度层的荷载分布。关于风荷载无量纲自功率谱的假定是叶丰[13]依据理论脉动风谱Davenport谱提出的,不考虑脉动风速谱沿高度变化。但实际情况下脉动风速谱是与高度相关的,尤其是对于部分极端风场,沿高度变化明显,不可忽略。杜宇等[14-15]根据某海洋平台的风场实测数据对冬季寒潮和超强台风两类强风过程的风场特性展开分析,对近海面不同高度处的脉动风功率谱进行了拟合,证明了脉动风实测谱和高度相关的von Karman经验谱的良好拟合关系。Zhao等[16]对经典的谱表示法引入时变相干性,用下击暴流和台风风场两个算例对该方法的精度和效率进行评估,风场实测数据的处理结果显示不同高度处的脉动风速功率谱具有显著的区别。

本文考虑沿高度变化的脉动风速谱,在原分段估计法的基础上,提出了一种可以考虑荷载谱沿高度变化的方法,以Kaimal脉动风谱为例推导了无量纲风荷载谱沿高度变化的修正系数。并选取某输电塔高频天平试验为算例,计算了修正系数对结构位移响应以及荷载沿高度分配的影响程度。

1 风荷载谱高度修正系数

1.1 理论分析

本节基于准定常假定和经验风谱推导脉动风荷载无量纲自功率谱的表达式,分析其沿高度是否变化。作用在结构高度z处的顺风向脉动风荷载为

(1)

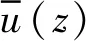
由此,顺风向脉动风荷载的自功率谱SF(z,f)可以表示为

(2)

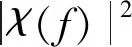
(3)

式(2)与式(3)作商可得高度z处的脉动风荷载无量纲自功率谱密度S′>F(z,f)(简称无量纲风荷载谱)为

(4)

常用的顺风向脉动风速自功率谱分为高度相关和高度无关两大类,其中高度无关的有Davenport谱

(5)

式中:Su(f)为高度无关的脉动风谱;k为表面阻力系数,与地面粗糙度有关;v10为10 m高度处平均风速;f为风荷载频率,Hz。

高度相关的以Kaimal谱为例

(6)

式中:k,v10含义同式(5);vz为高度z处平均风速,vz=(z/10)αv10,α按照地貌类型取值。

当采用Davenport脉动风谱,将式(5)代入式(4),易得无量纲风荷载谱S′>F(f)与高度无关;当采用Kaimal脉动风谱,将式(6)代入式(4),则有无量纲风荷载谱S′>F(z,f)与高度相关。为了更直观地表示后者的结果,以B类地貌下(k=0.005,α=0.15),v10=33 m/s为算例,计算不同高度处的无量纲风荷载谱S′>F(z,f),如图1所示,10～90 m内5个高度处的S′>F(z,f)曲线并不相同,无量纲风荷载谱沿高度变化,在较高频率区段(约0.1 Hz以上),随着高度增大S′>F(z,f)的值减小,在较低频率区段(约0.01 Hz以下),S′>F(z,f)的值随着高度增而增大;而Davenport谱随高度无变化。无量纲风荷载谱沿高度的变化情况与风荷载沿结构高度的分布相关,在高频天平试验的数据处理中,当采用不同的理论风谱,基底荷载谱沿高度的分段估计会得到不同的结果。

1.2 修正系数

对原分段估计法引入无量纲风荷载谱沿高度变化的修正系数。以10 m处无量纲风荷载谱为基准,修正系数定义为其余高度处无量纲风荷载谱与基准值的比值,由式(4)可得

(7)

式中:g(z,f)为高度修正系数;S′>F(10,f)为10 m处无量纲风荷载谱。

根据原分段估计法的求解理论,推导引入修正系数后的各层风荷载谱密度计算公式。关于无量纲风荷载谱的假定修正为

(8)

式(1)表达了脉动风荷载与脉动风速的关系,则作用在结构上高度z处的顺风向脉动风荷载均方根值σF(z)为

(9)

式中:σu′(z)为高度z处脉动风速均方根;其余参数意义同式(1)。

不同高度处的风荷载互功率谱密度可以表示为

(10)

式中: 下标“i”,“j”为不同高度处的结构段;cohF(zi,zj)为脉动风荷载相干函数,在准定常假设下可以用脉动风速相干函数代替,即cohF(zi,zj)=coh(zi,zj)。将式(8)代入式(10),有

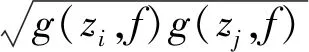
(11)

高频天平试验得到的基底弯矩功率谱密度SM(f)与不同高度处风荷载互谱密度SF(zi,zj,f)的关系为

(12)

将式(11)代入式(12)得到10 m处的无量纲风荷载自功率谱S′>F(10,f),再将S′>F(10,f)回代到式(11)得到zi,zj处的脉动风荷载互功率谱密度SF(zi,zj,f)为

SF(zi,zj,f)=

(13)

原分段估计法的脉动风荷载互功率谱密度SF(zi,zj,f)计算公式为

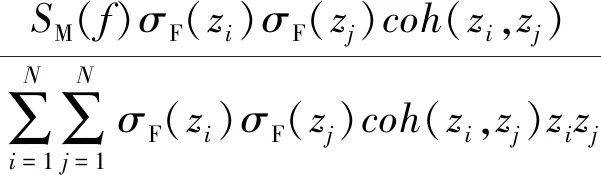
(14)

式中,参数意义同前文。

式(13)与式(14)相比引入了修正系数g(z,f),其余部分相同,可以用于脉动风速谱随高度变化的风场。

根据式(13)即可由天平试验的基底荷载谱SM(f)估算结构上各节点的脉动风荷载互功率谱SF(zi,zj,f),由于估算了结构不同高度处的脉动风荷载谱,可以考虑振型的非线性。广义模态力互功率谱SF*(i,j,f)为

(15)

式中:φi(z)为第i阶模态;i,j为不同的模态;z,z′为不同结构段的高度。

修正系数的表达式(7)中含有积分项不便于直接应用,将Kaimal谱代入积分项并拟合简化表达式。取10 m高度风速v10=33 m/s(后续算例塔架的临界风速),计算了不同高度处的脉动风速谱积分值,拟合得到积分项与高度呈线性关系

(16)

将拟合公式代入式(7)得到高度修正系数的表达式

(17)

式中,参数含义同式(6)。

当使用其他风谱时,将Kaimal谱的公式和参数替换为对应风谱,即可得到适用其他风谱的修正系数。

为更贴近工程实际应用,采用规范常用的Davenport谱为10 m高度处的基准,即将式(7)中10 m高度处的风速谱用Davenport谱替换,提出修正系数的另一形式

(18)

式中:Su,Daven(f)为Davenport脉动风速谱;S′>F,Daven(f)为Davenport谱对应的无量纲风荷载谱。

2 输电塔高频天平试验

2.1 试验概况

选取文献[17]中的高频天平试验数据进行算例分析。风洞试验的原型为某典型500 kV长横担钢管输电塔,塔架总高76.7 m,呼高42.0 m,基底根开16.16 m,有上、中、下3层横担,模型制作缩尺比为1∶120。对原型结构进行动力特性分析,得到塔架前3阶模态如表1所示。

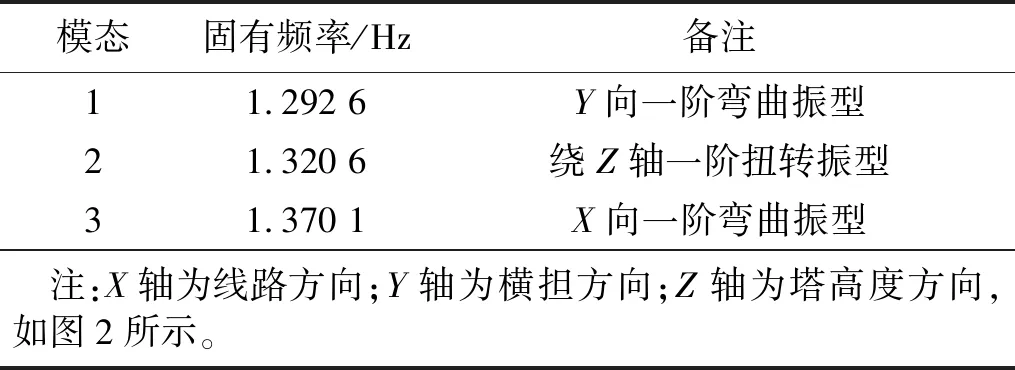
表1 塔架原型动力特性Tab.1 Dynamic characteristics of tower prototype

风洞试验布置如图2所示。试验采用的地貌类型为B类地貌,基本风压0.7 kN/m2。试验段参考点高度为0.627 m,参考点平均风速为12 m/s。

图2 风场布置(0°风向角工况)Fig.2 Wind field layout (0° wind direction angle condition)

2.2 基底荷载谱的半刚性修正

由于格构式结构的模型刚度较小,其一阶振型频率处于结构荷载谱频带以内,因而共振作用比较明显,对结构动力荷载的影响不可忽视,需要对试验得到的基底荷载谱进行半刚性模型修正。本文采用夏亮和郜良浩等[18]的半刚性模型荷载谱修正方法对结构基底弯矩谱进行修正。

0°风向角下顺风向弯矩荷载谱的修正结果,如图3所示。

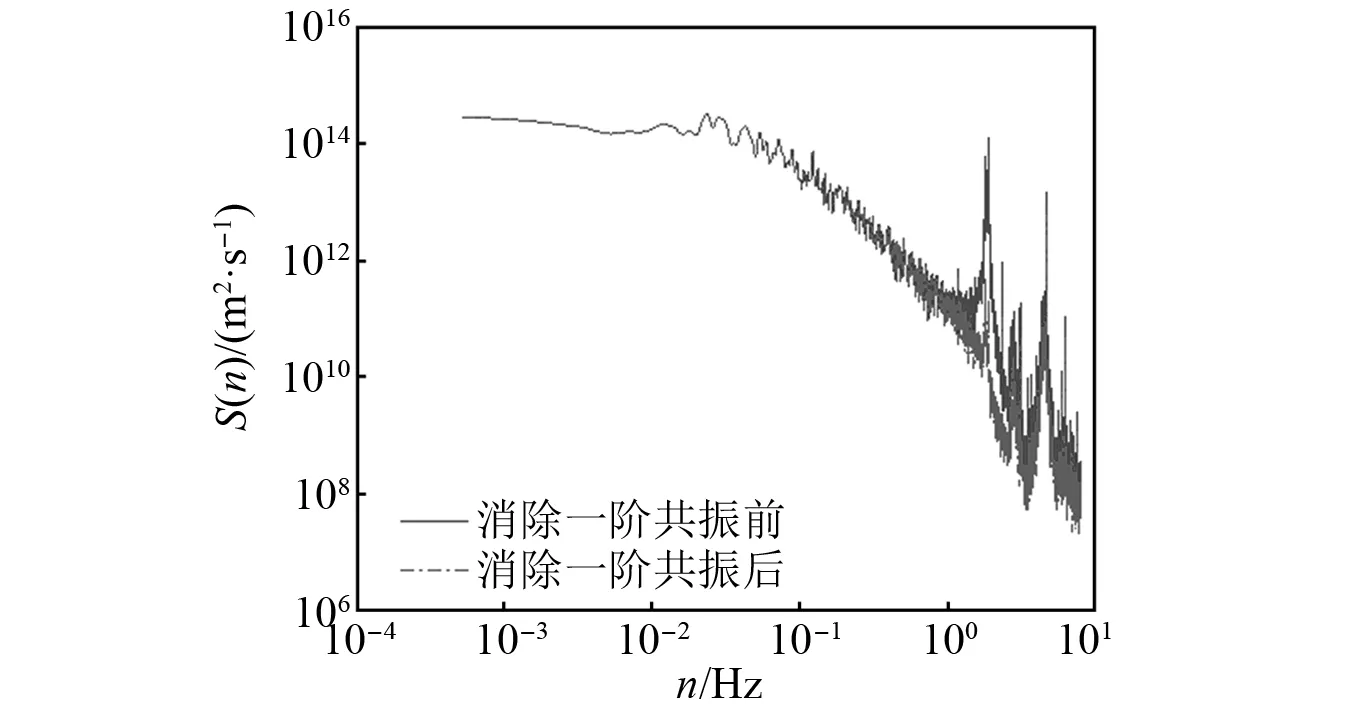
图3 输电塔顺风向基底弯矩谱Fig.3 Downwind base bending moment spectrum of transmission tower

3 算例分析

3.1 顺风向脉动位移响应

由半刚性修正后的基底弯矩谱SM(f),按照式(13)和式(15)计算结构不同高度处风荷载互功率谱SF(zi,zj,f)和广义模态力功率谱SF*(f)。

高度z处结构的脉动位移响应均方根值σq(z)可由背景加共振法[19-20]求得,如式(19)～式(21)

(19)

式中:σqi,b(z)为第i阶位移响应背景分量;σqi,r(z)为第i阶位移响应共振分量;n为参与计算的振型数量。

(20)

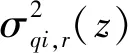
(21)

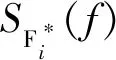
参与计算的模态数量对塔顶节点的顺风向位移响应的影响,如图4所示。结果显示第1、第2阶模态对位移结果无贡献,第4～第10阶模态是否参与计算对位移的影响也很小,第3阶模态贡献占绝大部分。这是由于第3阶模态对应X向一阶弯曲振型,与0°风向角下风荷载方向一致,对顺风向位移响应起到控制作用,在后续计算顺风向位移时只考虑第3阶模态。

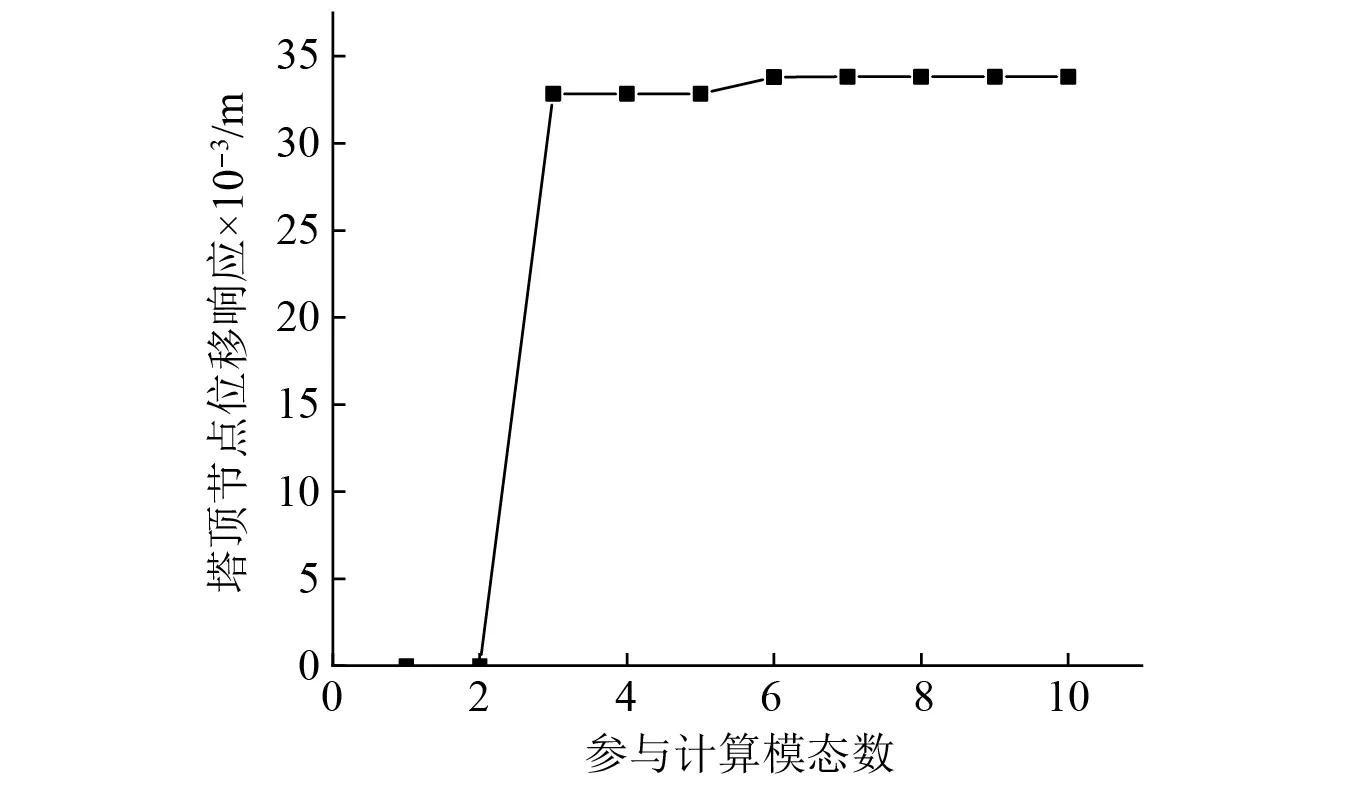
图4 不同计算模态数下塔顶节点位移响应Fig.4 Displacement response of tower top node under different calculation mode numbers

按照原分段估计法和本文提出的修正方法分别对基底荷载谱进行分段估计,计算对比塔架的位移响应。0°风向角下塔顶节点顺风向位移结果,如表2和图5所示。由表2和图5可知,修正系数对塔顶位移背景分量影响很小,修正前后变化幅度仅0.33%;对共振分量的影响较大,变化幅度为25.94%。总位移响应变化较小,这是由于算例塔架刚度较大,背景分量在位移响应中占比较高[21],共振分量的变化在总位移中反映不明显。

表2 塔顶节点位移分量Tab.2 Displacement component of tower top node

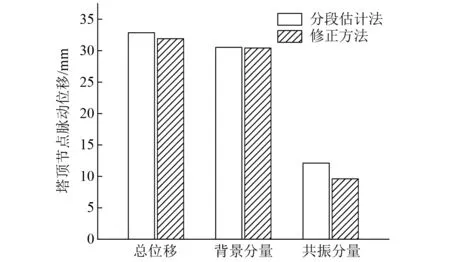
图5 塔顶节点位移及其分量Fig.5 Node displacement and its components at the top of the tower

3.2 不同频率下修正系数对比

为分析修正系数对位移背景分量和共振分量的影响差异,取不同频率处的修正系数g(z,f)进行比较。不同频率处修正系数沿塔架高度的变化情况,如图6所示。f1为塔架X向一阶弯曲振型频率。可见0.1f1～1.0f1频率下修正系数小于1且随高度上升逐渐减小。这是由于修正系数的定义为高度z处无量纲风荷载谱与10 m高度处无量纲风荷载谱的比值,由图1可知,在高频率区段内,随高度上升,无量纲风荷载谱降低,在低频率区段内规律相反。结构基频f1=1.370 Hz,f1和0.1f1处于图1中高频率区段,所以此频率范围内修正系数小于1且随高度升高而减小。

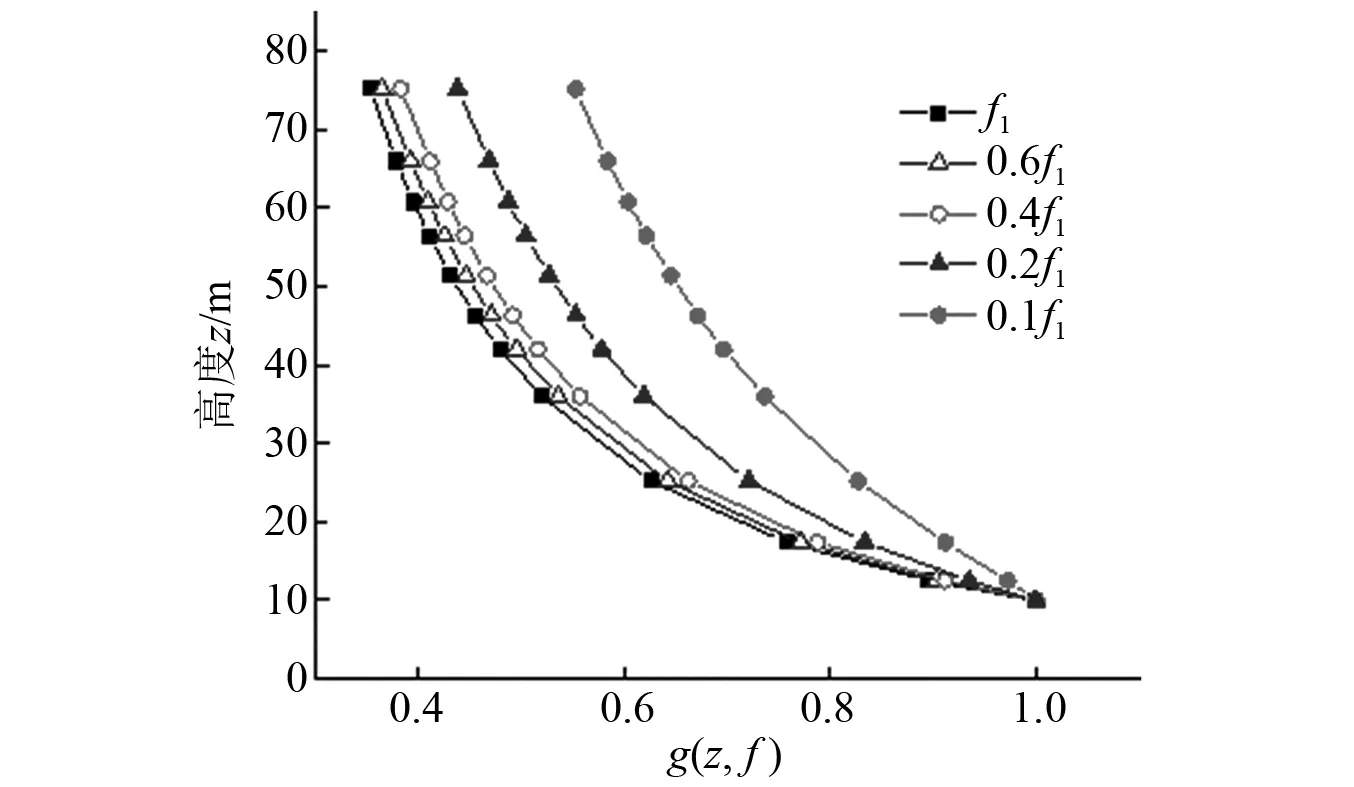
图6 不同频率下修正系数沿高度变化Fig.6 Variation of correction coefficient along height at different frequencies

定义基底荷载谱沿高度的分配系数为

η(zi,zj,f)=SF(zi,zj,f)zizj/SM(f)

(22)

式中,参数意义同前文。

此系数代表基底荷载谱分配至各节段的比例。结构基频下塔架各节段的风荷载自功率谱分配系数,如图7所示。修正公式计算的塔身下部荷载谱分配系数更大,表明更多的风荷载被分配至塔身下部。

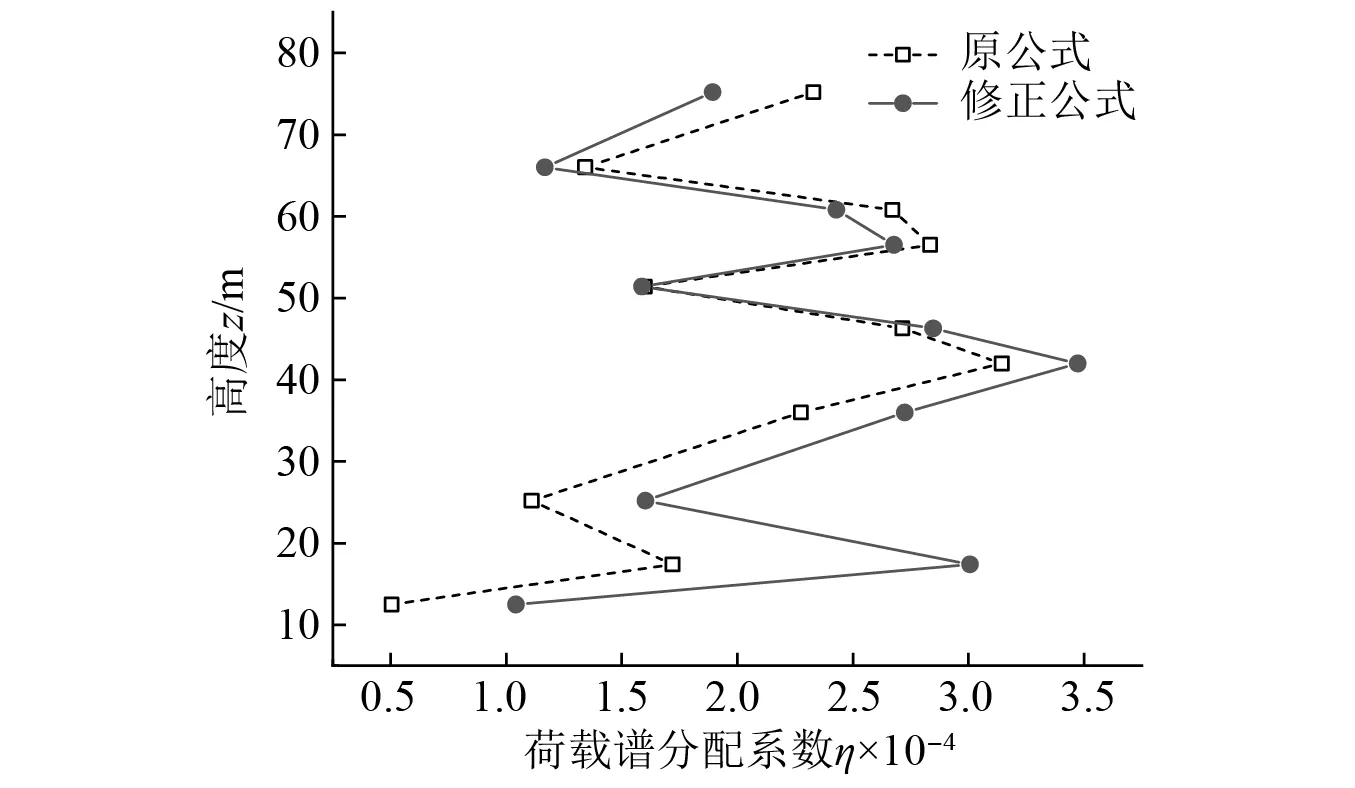
图7 结构基频下的风荷载自功率谱分配系数Fig.7 Distribution coefficient of self-power spectrum of wind load at structural fundamental frequency

由式(20)可知,结构的脉动位移背景分量由荷载谱在全频率范围的积分值计算得到,修正系数在高低频段的影响相反,相互抵消,故修正影响不大。而共振分量由结构自振频率附近的荷载谱控制[22],见图7,在f=f1处,修正后更多的风荷载被分配至塔身下部,根据塔顶位移的影响线,塔身下部的荷载对塔顶位移的作用小,因此修正后塔顶位移的共振分量有显著减小。

3.3 修正系数对不同刚度结构响应的影响

由3.1节可知,修正系数对位移响应共振分量影响更大,而刚度较小的高耸结构,如格构式桅杆塔、单管塔,共振分量在位移响应中占比较高,推测此类结构的响应受修正系数的影响显著。限于缺少相关结构模型,本节通过改变频域法计算中的结构振型频率来模拟结构刚度的改变,分析修正系数对不同刚度结构的影响差异。结构原频率f1=1.370 Hz,以原频率的0.1倍为梯度进行参数调整,最低调整至0.4f1,符合实际工程中部分超高层建筑和高耸结构的自振频率。塔顶羊角处节点的顺风向位移结果如表3和图8所示。

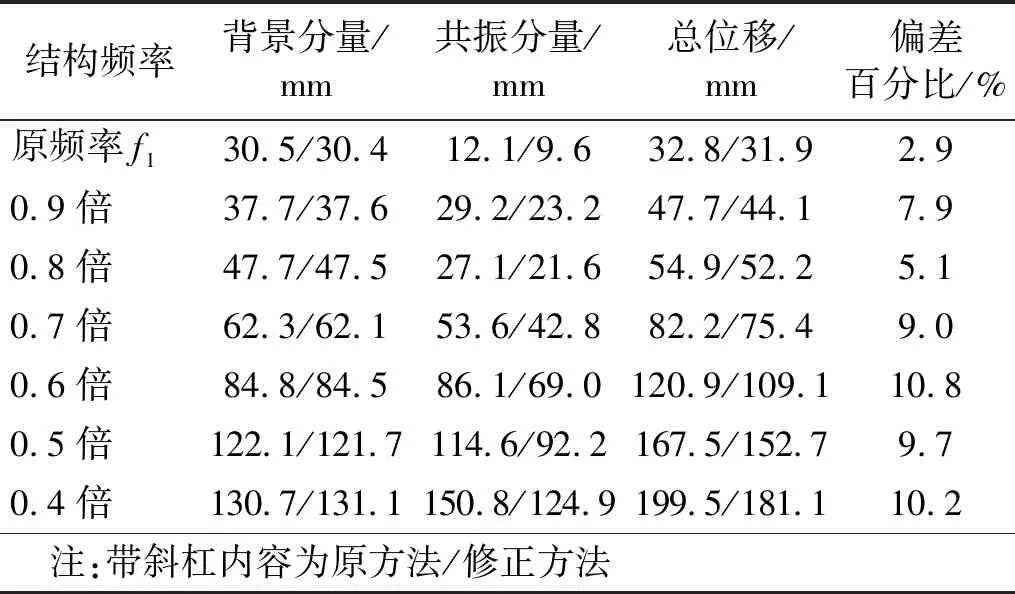
表3 塔顶节点顺风向位移响应计算结果

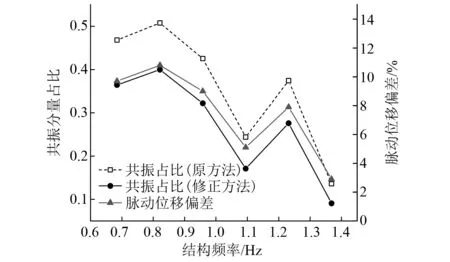
图8 不同刚度结构的位移响应结果Fig.8 Displacement response results of structures with different stiffnesses

由图8可知,随着频率降低,结构的刚度减小,共振分量在位移响应中的占比整体呈增大趋势。在0.4f1～1.0f1内,修正前后计算的塔顶节点的脉动位移偏差逐渐增大,在结构频率降低至0.4f1时,脉动位移偏差达到10%左右。这是由于修正方法计算的共振分量较小,随着结构刚度降低,共振分量在脉动位移响应中占比提高,所以修正后的脉动位移低于原方法计算值,且差值随频率降低而增大。

值得注意的是,以上分析的结论是以随高度减小的Kaimal谱为例得出的。本文方法同样可以运用到在某一高度突然增大的特异风中。显然,对于沿高度增大的风速谱,会有更多的风荷载被分配至结构的上部,则原方法将低估结构的位移响应。

4 结 论

本文通过理论推导对高频天平试验脉动风荷载分段估计法进行了修正,并以某输电塔天平试验数据为算例进行了对比分析。得到以下几点结论:

(1) 在脉动风速谱沿高度变化的风场中,结构上的无量纲荷载谱沿高度变化,本文抛弃了分段估计法中无量纲风荷载谱沿高度不变的假定,提出的修正方法可以方便地考虑荷载谱沿高度的变化,具有更高精度和更广的适用性。

(2) 提出了风荷载谱高度修正系数,该系数对结构位移共振分量影响较大,对背景分量影响较小。对刚度较大的结构,共振分量在总响应中占比较低,修正前后结果差异不大,原分段估计法依然适用。

(3) 对于柔性较强的高耸结构,如桅杆塔、单管塔等,其共振响应占比较高,修正前后的响应计算结果有明显差别。对于沿高度减小或变大的脉动风速谱而言,原分段估计法不考虑风荷载谱随高度变化,会高估或低估结构的位移响应。