基于RANS/LES混合方法的箱梁气动导纳函数研究

张伟峰, 张志田

(1. 华北水利水电大学 土木与交通学院,郑州 450045;2. 海南大学 土木建筑工程学院,海口 570228)

大跨度桥梁的主梁断面形式多样,主要有整体式钢箱梁、分离式钢箱梁、钢桁梁、混凝土箱梁、混凝土双主梁等。由于断面形式的不同,气流流经断面时占据主导地位的流动现象也不同 。例如对于扁平钢箱梁,断面周围的流动大部分为附着流,仅在转角和尾部有较弱的分离流。相反,对于分离式双箱梁、混凝土双主梁等会在断面周围和尾部产生显著的涡脱。CFD(computational fluid dynamics)模拟桥梁气动力的关键是对这些流动现象进行准确的模拟。

RANS(Reynolds-averaged navier-stokes)由于计算花费少,在当前的工程中得到广泛应用。但是RANS由于对湍流黏度过大的模化,极大的抑制了剪切层失稳和小尺度运动的生成与演化,仅能预测到大尺度和低频运动,这对于时均气动力的求解是可行的,却难以应用于非定常气动力的求解,如抖振力。LES(large eddy simulation)是一种真正的非定常模拟方法,它对大尺度的脉动进行直接求解,而只对具有普适性的小尺度脉动进行模化。在近壁面由于湍流尺度Lt正比于到壁面的距离y,因此越靠近壁面,积分尺度越小,需要的空间、时间分辨率就越高,现阶段的计算能力很难满足高雷诺数壁面流的需求。Spalart[1]指出,对于一个雷诺数1×106左右的简单边界层流动,网格数目和时间步数也分别达到了惊人的1×1011和1×107,Spalart估计在2045年有望实现LES在工程问题中的广泛应用。需要注意的是,虽然LES已经被大量应用于桥梁风工程中,但已有研究的网格精度并没有达到LES的标准而形成VLES(very large eddy simulation)模拟,从而不能准确模拟含能区的湍流结构与湍流能量,导致模拟结果与网格尺寸相关[2-4]。目前,严格的LES主要用于自由剪切层和低雷诺数的壁面流。在可见的未来,同时满足网格分辨率和时间分辨率的LES在桥梁风工程中的应用仍很难普及[5-6]。

RANS/LES混合方法属于尺度解析模拟(scale-resolving simulation,SRS),在近壁面的平衡湍流区域中采用RANS,而在远离壁面的非平衡区域采用LES。这样既降低了LES在近壁面处的计算代价,又获得了相对准确且丰富的非定常信息,有效实现了计算效率和计算精度的统一。事实上,RANS/LES混合方法正是基于在当前的计算条件下,满足用适中的计算量提供工程应用所需要的非定常信息而提出的[7]。三维的RANS/LES混合方法在航空航天、叶轮机械、汽车等领域已取得了较为广泛的应用,但在桥梁风工程中却应用较少。Bai等[8]采用当三维DES(detached eddy simulation)模拟了箱梁断面的静三分力系数并识别得到了颤振导数,研究表明当三维DES用于桥梁气动力分析时具有明显的优势和较高的精度;魏志刚[9]采用IDDES(improved delayed DES)对箱梁断面的静力三分力系数、表面压强分布、流场信息进行了详细的研究;Zhang等[10]采用DDES(delayed DES)研究了展向布置的吸气孔对桥梁涡脱的影响。

气动导纳函数是大跨度桥梁抖振分析的关键参数,用来描述作用在结构物上气动力的非定常特性。RANS/LES混合方法由于具备对非定常流动信息的捕捉能力,因此是研究气动导纳函数非常有利的工具。遗憾的是,相比于RANS/LES混合方法在桥梁时均流场的研究,在非定常气动力的研究方面更加稀少。大量研究表明桥梁气动导纳函数与来流的风场特性,如湍流度、湍流积分尺度等有关[11-12]。实桥顺风向的湍流积分尺度通常位于80～300 m,约为桥梁宽度W的3倍～10倍,竖风向的湍流积分尺度通常位于15～50 m,约为桥梁宽度W的0.5倍～2.0倍。传统的基于格栅湍流场的风洞试验,对于积分尺度的模拟严重失真,特别是顺风向积分尺度,多数试验位于0.1W～0.5W[13-14]。考虑到积分尺度对气动导纳函数的影响,把风洞试验识别的气动导纳用于实桥的抖振分析,必然会对结果带来影响。虽然可以借助于大尺寸风洞或者主动风洞实现大积分尺度湍流的模拟,但这两者都需要较大的投入。

满足自然风场特性的湍流数值模拟,一直是风工程领域的热点。Huang等[15-20]先后分别提出了不同的各向异性湍流场模拟方法,可以实现任意特性脉动风的模拟。通过将脉动风场模拟方法和RANS/LES混合方法相结合,可以实现任意积分尺度湍流场下桥梁非定常气动力的模拟。

本文选取3种典型的RANS/LES混合方法,即:SAS(scale-adaptive simulation)、SBES(stress-blended eddy simulation)、WMLES(wall-modeled LES)。在前人研究的基础上提出了一种改进的脉动风合成方法,该方法既满足无散度条件,同时又可以实现任意空间相关性和时间相关性的风场。在均匀来流下,选取流线型箱梁断面和分离式双箱梁断面,通过表面均匀压强分布和周围流动特征的比较,探讨了3种混合方法的特点和适用性。分别在与实际风环境相似的大湍流积分尺度来流下,和风洞试验格栅湍流场相似的小尺度来流下识别了箱梁断面的气动导纳函数,研究了大积分尺度湍流对箱梁气动导纳的影响。

1 RANS/LES混合方法

自1997年Spalart等提出DES以来,近20年来研究者们提出并发展了多种RANS/LES混合模型。不幸的是,并不存在一种普适的可以应用于任意流动的RANS/LES混合模型。针对于桥梁风工程,由于各类桥梁断面的形式不同,占据主导地位的流动现象也不同,各种混合模型的表现不一。

1.1 SAS方法

SAS方法严格意义上来说不属于RANS/LES混合模型,但考虑到它在定常流动区域表现出RANS的特性,而在脉动显著的区域表现出LES的特性,因此通常把它归类到RANS/LES混合模型。SAS模型最早由Menter等[21]提出,并由Menter和Egorov[22]改进。它与RANS模型最主要的区别是引入冯卡门长度尺度LvK。LvK包含了速度的一阶导数和二阶导数,它只与当地流动有关而与网格尺度无关。当流场中存在脉动时LvK减小,而LvK的减小会使得湍流黏度变小,从而使小的脉动得以保留和发展。

SAS通过在k-ω模型的ω方程中引入源项QSAS

QSAS=max(T1-T2,0)

(1)

(2)

(3)

式中:T1,T2为组成源项的附加项;ρ为流体的密度;k为湍动能;ω为比耗散率;xj为空间坐标(j=1,2,3);S为应变率张量Sij的模;η2,σφ,C,κ为常系数,分别为η2=3.51,σφ=2/3,C=2,κ=0.41。

L为湍流长度尺度

(4)

式中,cμ为常数0.09。LvK为冯卡门长度尺度

(5)

式中,U′,U″分别为速度的一阶、二阶导数

(6)

式中:Ui为流动速度;xk为空间坐标(k=1,2,3)。式(1)中:T1项通过LvK来分辨小尺度的涡;T2项是为了保障在定常流时模型能回归到RANS。从以上分析可以看出,SAS模型通过LvK的变化,使得非稳态流域的涡发展,比如钝体断面周围以及尾部流动区域。因此在均匀来流时,SAS可以应用于具有显著流动不稳定现象的钝体断面,但是对于流动不稳定现象较弱的流线型断面,SAS有可能会退化为RANS。

1.2 SBES方法

Spalart早期提出的DES模型,对RANS和LES计算域的判定严重依赖于当地网格尺度,即对网格有强烈的依赖性。当进行网格的加密操作时,有可能在边界层内激活LES,此时网格尺度过于粗糙,无法准确模拟求解涡的脉动,导致雷诺应力耗损,从而诱发边界层的提前分离,也就是所谓的网格诱导分离(grid induced separation,GIS) 问题。为了克服GIS问题,Spalart等[23]通过引入延迟函数来保障在网格加密时,边界层仍然处于RANS,这就是所谓的DDES。

DES类模型存在的另外一个问题是,在RANS和LES的交接处附近存在“灰区”。在这个过渡区由于边界层内部湍流黏度的影响,使得LES区域的小尺度脉动得到抑制,从而解析的雷诺应力也较小。在“灰区”以外,湍流黏度的影响减小,小尺度脉动得以发展,从而解析的雷诺应力增大。由于“灰区”的存在,导致了边界层内部和外部的对数率不匹配 (log layer mismatch,LLM) 问题。LLM通常会导致错误的壁面摩擦因数。为此,Shur等[24]提出了IDDES方法来消除LLM的影响。

近年来,Menter[25]提出了SDES(shielded detached eddy simulation)方法和SBES方法,两种方法都基于一种新的屏蔽函数,该屏蔽函数可以有效解决RANS/LES混合方法普遍存在的GIS问题和LLM问题。Menter建议使用SBES方法代替现有的DES、DDES、IDDES方法。

SBES方法是把RANS和LES通过屏蔽函数结合起来,以总应力的形式表示为

τij,SBES=fSBESτij,RANS+(1-fSBES)τij,LES

(7)

式中:τij,RANS为总应力;fSBES为屏蔽函数,在边界层内fSBES=1,在流动分离区和自由剪切流中fSBES=0;τij,RANS为总应力中对应RANS的部分;τij,LES为总应力中对应LES的部分。

Menter等[26]将其应用于槽道流、圆柱绕流、汽车绕流、扩散器等,认为SBES方法在附着流、大尺度分离流、中等尺度分离流等流动问题中都有着优异的表现。总的来说它具有如下的特点:现有的RANS类湍流模型和LES类湍流模型可以任意组合到SBES方法中;在网格细化时对边界层内的RANS提供保护,防止GIS的发生;在RANS和LES交界处,可以实现快速过渡,减少“灰区”,消除LLM;既可以应用于显著流动分离的钝体断面也可以应用于附着流和小尺度分离流的流线型断面;计算花费小等。

1.3 WMLES方法

为了避免LES的计算花费随雷诺数Re的指数增长,可以在靠近壁面的对数率层使用RANS湍流模型,而在网格分辨率足够时的外层使用LES湍流模型,该方法即为WMLES方法。在平行于壁面的方向,相比于完全求解的LES,WMLES方法的网格尺寸可以显著增大。

本文采用的WMLES最早由Shur等提出。它将普朗特混合长度和Smagorinsky模型结合起来,对于湍流黏度系数νt有

νt=min[(κdw)2,(CSmagΔ)2]·S·
{1-exp[-(y+/25)3]}

(8)

式中:dw为网格中心到壁面的距离;κ,CSmag为常数,κ=0.418 7,CSmag=0.2;y+为无量纲距离; Δ为亚格子滤波尺度,它同时考虑了网格的各向异性和到壁面的距离。

Δ=min(max[Cw·dw,Cw·hmax,hwn];hmax)

(9)

式中:hmax对于六面体网格为网格最大边长;hwn为垂直壁面方向的网格尺度;Cw为常数,Cw=0.15。从构造上来说,WMLES在近壁面采用0方程的普朗特混合长度、远离壁面区域采用Smagorinsky涡黏模式,具有构造简单、容易收敛的特点,是最简单的RANS/LES混合方法。同时,WMLES在计算中的表现也具有这两种模型的特点,如对逆压梯度、分离再附流动等现象无法准确预测,总体表现不如两方程的RANS/LES混合方法。

2 CFD数值模型

在以往研究的基础上,首先提出了一种入口湍流合成方法,该方法能够模拟任意湍流特性的风场。

2.1 入口湍流模拟

为了模拟桥梁断面在湍流来流下的气动力,计算域的入口需要设置湍流边界条件。满足自然风场特性的湍流数值模拟,一直是风工程领域的热点。基于Huang等提出的DSRFG(discrete and synthesizing random flow generation)方法,Castro等引入了一个时间尺度,用来调整生成风速时程的时间相关性,并将此方法命名为MDSRFG(modified DSRFG)。为了克服DSRFG生成风速时程的相干性与频率无关的缺点,Aboshosha等引入了一个与频率有关的积分尺度,但是由于该参数的引入,使得CDRFG(consistent DRFG)方法不再满足无散度条件。综合MDSRFG方法和CDRFG方法,本文同时引入时间尺度因子和与频率有关的积分尺度,并通过修正使模拟的风速满足无散度条件,具体过程如下。

在CDRFG方法的基础上,同时借鉴MDSRFG方法,在脉动风速时程的表达式中引入时间尺度,此时脉动风速时程ui(i=1,2,3)可以表示为

(10)

其中

(11)

(12)

为了满足连续性方程,波数k与参数p,q的关系应该满足

(13)

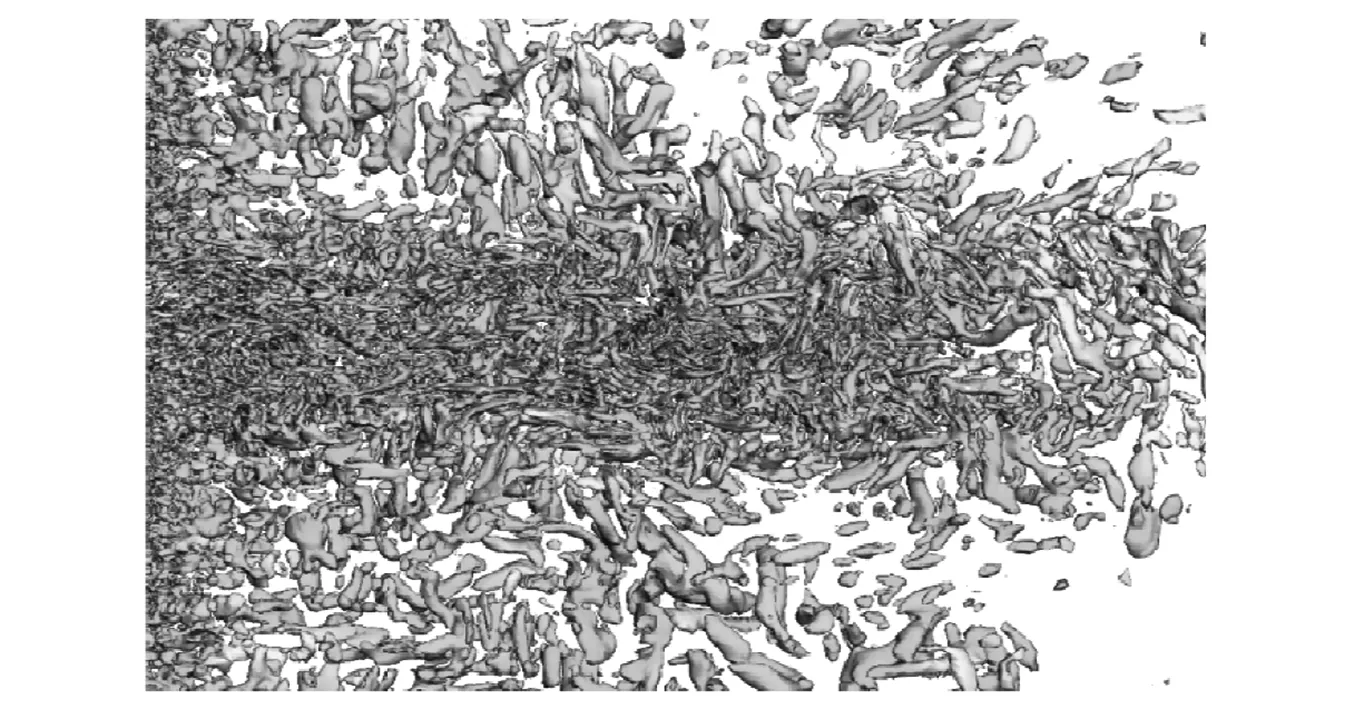
图1 空流域中的瞬时漩涡结构Fig.1 Instantaneous vortex structures in the empty domain

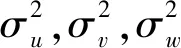
图2 模拟功率谱与入口功率谱比较Fig.2 Comparison of the simulated power spectrum and inlet power spectrum

图3 模拟风场的时间相关性Fig.3 Time correlation of the simulated wind velocity components

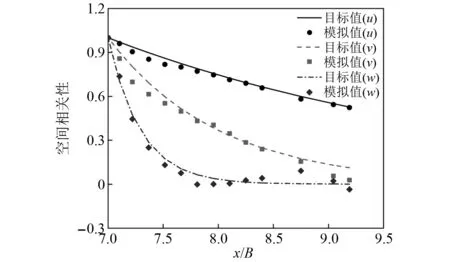
图4 模拟风场的空间相关性Fig.4 Spatial correlation of the simulated wind velocity components

此外,本文还验证了流场的均匀性,结果表明桥梁断面所处位置范围内的流场特征具有很好的均匀性,限于篇幅这里不再给出。

2.2 数值计算工况

选取扁平钢箱梁作为研究对象,扁平钢箱梁因具有流线化的气动外形,被大跨度桥梁广泛采用。通常,在其断面周围除了棱角处有小范围的流动分离现象外,大部分区域处于附着流状态,计算模型尺寸如图5所示。图5中:s为以断面迎风端前缘为起始点,沿着顺时针方向各个压强监测点到起始点的距离与断面周长比值的无量纲距离。计算域与边界条件如图6所示。断面前缘到入口处的距离为8B。断面尾缘到出口处的距离为16B,上下边界距离断面形心的距离为8B,对应的模型阻塞比为0.64%,小于风洞试验模型阻塞比不应超过5%的要求。参照研究者以往研究成果,计算域展向长度选为B[27]。计算域的选取一方面是为了尽量减少边界条件对近壁面流动和尾流流动的影响;另一方面当采用人工合成的速度场作为入口时,减少非物理的流场在计算域中引起的压强脉动对断面压强的影响。边界条件的设定为,入口处采用速度进口,平均速度U为8.0 m/s,对应的雷诺数Re=UB/ν=3.7×105,其中:ν为运动黏度系数,出口处为纽曼边界条件,前后边界和上下边界都采用周期性边界。

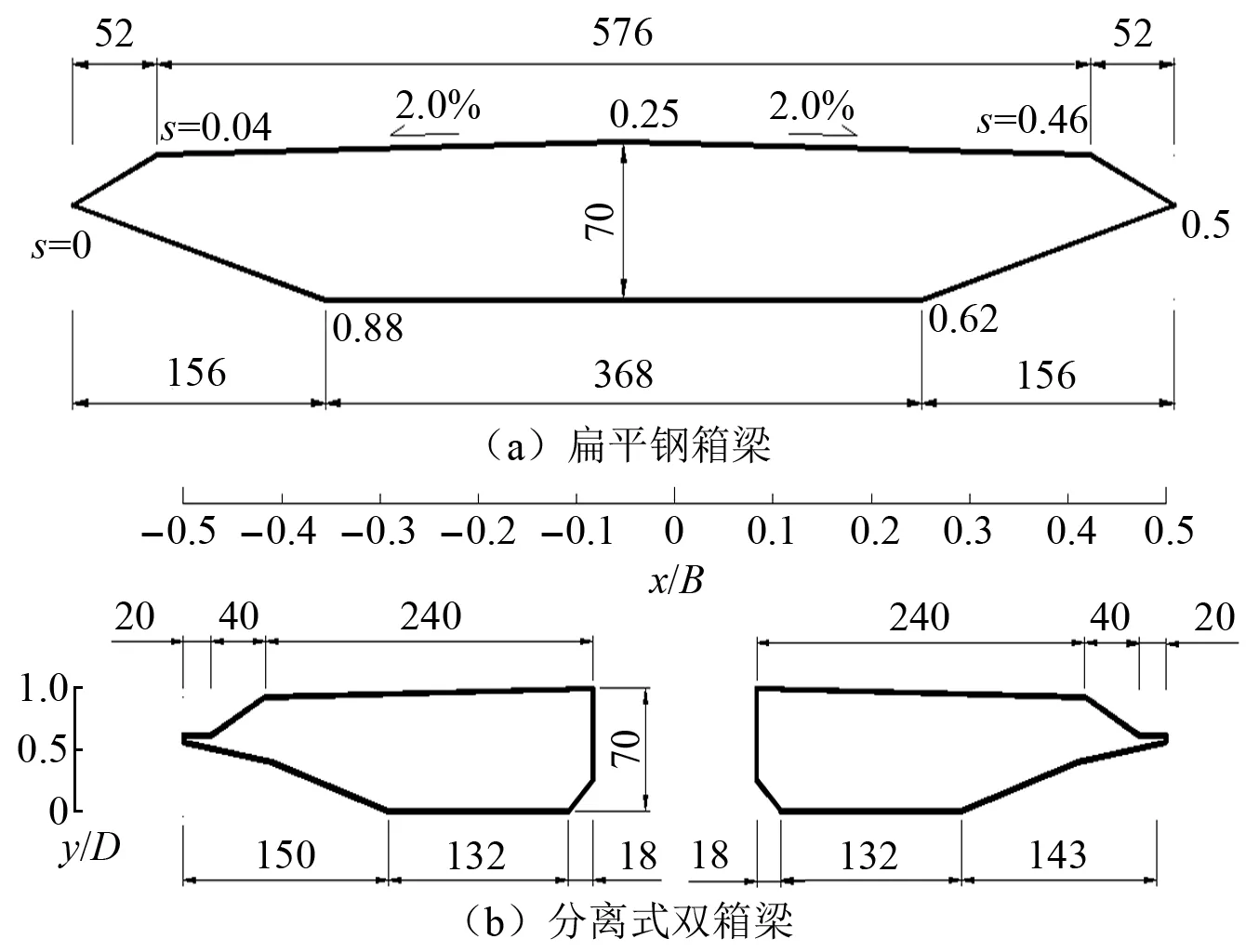
图5 桥梁断面尺寸(mm)Fig.5 Geometry of the bridge section (mm)

网格采取混合型的划分策略,在模型周围采用结构化的六面体网格,在此六面体网格之外采用四面体网格和六面体网格对断面周围和尾流区进行加密,加密区之外恢复为结构化的六面体网格。此外,为了减少湍流脉动从入口处到模型所在位置处的衰减,需要对此区域的网格进行加密,网格大小为0.029B。断面周围边界层的网格尺寸如表1所示。表1中:x,y,z分别为顺流向、横向和竖向。表1中给出了3种不同的网格尺寸,用以验证计算结果的准确性,其中网格3为在网格2的基础上继续加密而来的,用于LES计算。网格1对应的计算域网格如图7所示。数值计算格式设置如下:动量方程采用有界中心差分格式,压力采用二阶迎风格式,时间离散采用有界二阶隐式格式,时间步长保障CFL数(courant number)小于1.0,压力、速度耦合采用PISO(pressure-implicit with splitting of operators)算法。

表1 边界层网格尺寸Tab.1 Grid size in the boundary layer

图7 计算域网格Fig.7 Computational mesh

3 数值计算结果

采用SAS、SBES、WMLES计算了均匀来流下箱梁断面的气动力,分别从气动力系数和流场特征分析了这3种方法的特点。然后采用SBES方法,分别在大尺度湍流和小尺度湍流下,识别了气动导纳函数。

3.1 压强模拟结果

在网格2,分别采用SAS、SBES、WMLES在均匀来流下得到压强系数Cp沿箱梁断面的时均值和脉动均方根值σcp,如图8所示。图8中同时给出了LES模拟结果以及Yan等[28]风洞试验均匀流场中的结果作为比较。LES的网格尺寸如表1中网格3所示。需要注意的是,虽然LES所用网格尺寸远小于其他两种网格尺寸,但平行于壁面方向的网格尺寸仍不足以满足LES的网格尺寸要求。

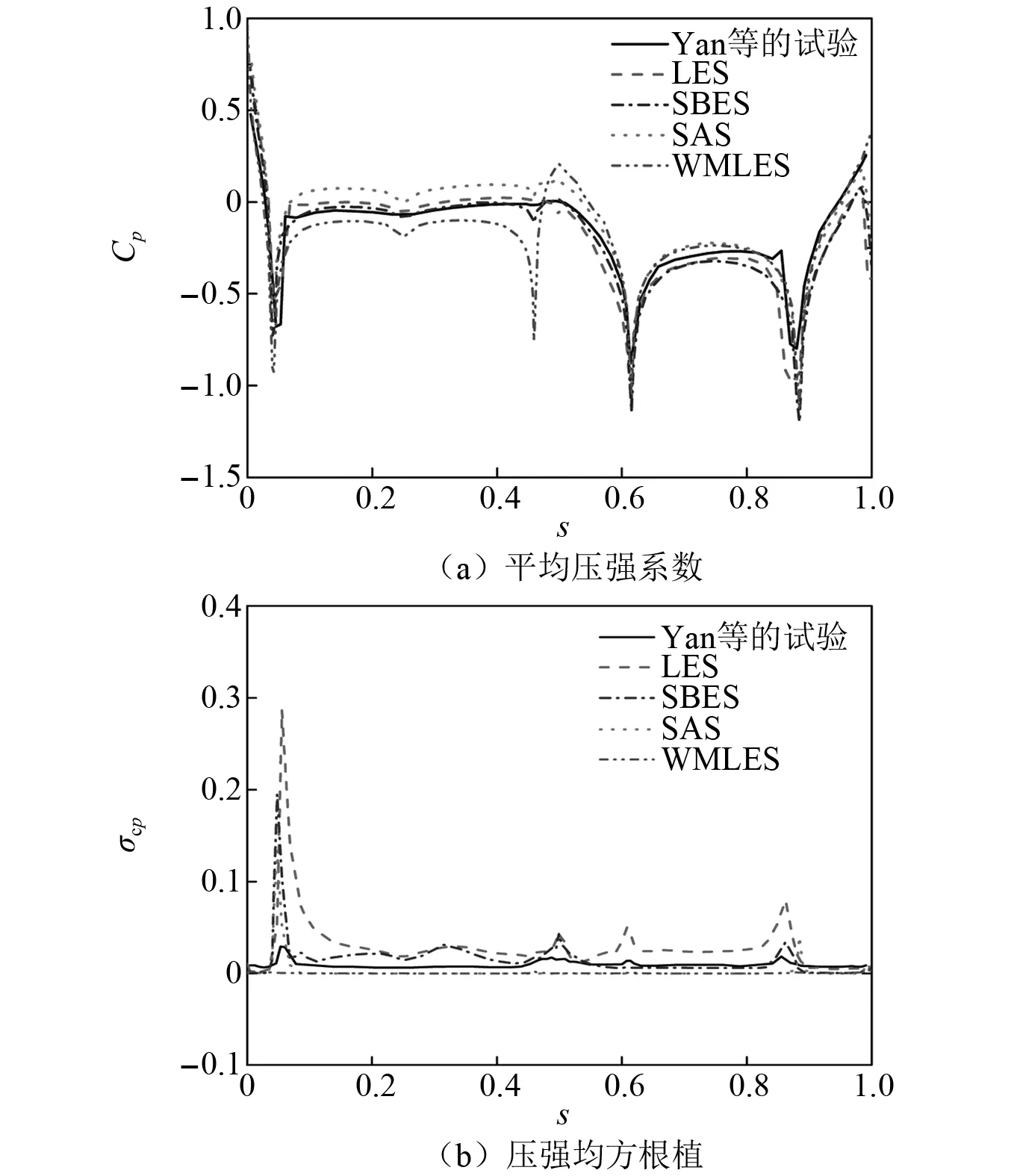
图8 压强系数沿箱梁表面分布图Fig.8 Distribution of pressure coefficients along the surface of box girder

由图8可知,对于平均压强系数,箱梁顶板处SAS的结果明显大于试验值,相反WMLES的值小于试验值。除了顶板以外,其他位置处SAS和WMLES的值都与试验值吻合较好。整体上,SBES和LES的结果基本一致,都与试验值吻合较好。对于压强的均方根值,SAS和WMLES的结果小于试验值,LES的结果大于试验值,SBES的结果与试验值较为接近。数值模拟结果与试验值的差别:一方面由于数值模拟的监测点布置在靠近断面的拐点处,而这在试验中是不可能的,因此造成拐点处的数值大于试验值;另一方面由于风洞试验的流场并不是完全的均匀来流,湍流的存在抑制了断面周围的脉动。

Q准则显示的流场瞬时漩涡结构,如图9所示。用流向速度V进行渲染。由图9可知,在断面周围以及尾部区域SBES方法都展示出了丰富的三维漩涡结构,流动结构与LES类似。相比于SBES方法,SAS方法和WMLES方法的流动呈现出二维特性。由于SAS方法在建立之初就是为了应用于大的流动分离现象,当流动中存在显著的流动不稳定时,方程中的长度尺度LvK会相应调整以降低湍流黏度,从而释放更多的涡。由图9(c)可知,在前缘风嘴与上下表面的转折处有漩涡结构,其他区域流动都呈现出二维特性。这说明SAS方法并不适用于这种流线型的箱梁断面,在流动的大部分区域SAS都表现为URANS(unsteady RANS)。WMLES方法在剪切层分离处会产生较大的湍流黏度,此外WMLES没有屏蔽函数,会产生较大的“灰区”,造成RANS模化的湍流黏度通过对流进入LES区域,对LES区域的湍流脉动带来较大的抑制。为了促进湍涡的发展,WMLES方法需要配合湍流入口使用。

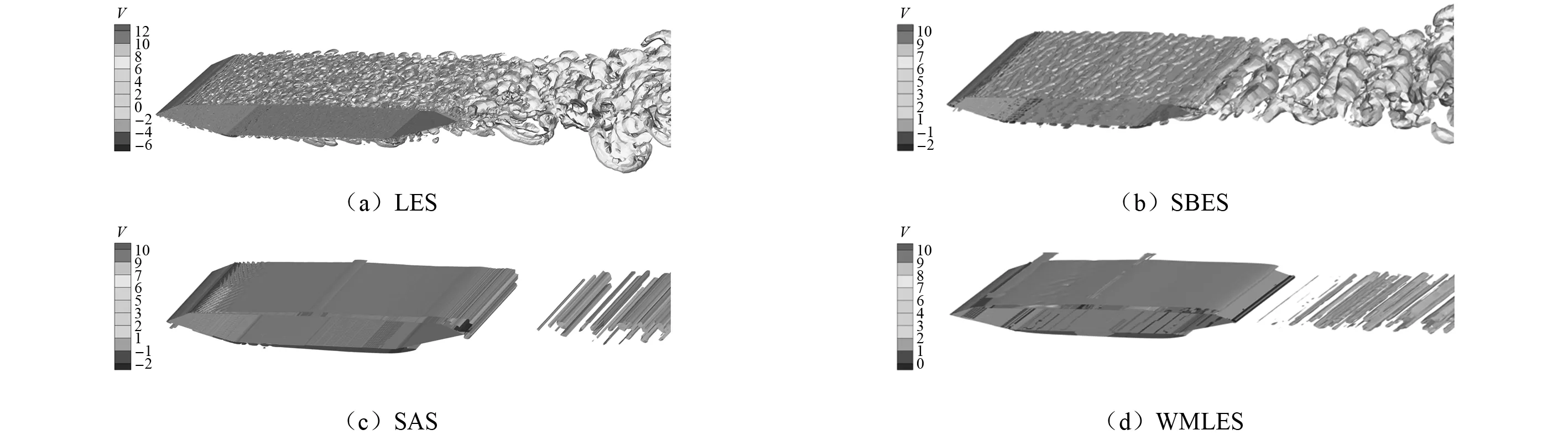
图9 不同RANS/LES方法的流场瞬时漩涡结构Fig.9 Instantaneous vortex structures with various RANS/LES models

为了进一步验证RANS/LES混合方法对复杂流动现象的预测能力,分别将3种混合方法用于分离式双箱梁断面。分离式双箱梁由于上下幅箱梁的相互干扰,断面周围的流场异常复杂。分离式双箱梁的断面尺寸见图5(b)。分离式双箱梁断面的平均压强和脉动压强,如图10、图11所示。图10、图11同时给出了Li等[29]的风洞试验结果以及吴步晨[30]的LES模拟结果,雷诺数Re=UD/ν=4.0×104(D为模型高度),与本文的3.85×104接近。由图10、图11可知,除了上游间隙的平均压强和下游箱梁下表面的脉动压强,SBES方法的结果与试验结果和吴步晨的LES结果吻合较好,显示出SBES方法对复杂流动现象较强的预测能力。SAS方法对下游箱梁平均压强的预测与试验结果有一定偏差,但是对间隙压强的预测在3种方法中与试验值却最为接近。同时从仅有的下表面脉动压强风洞试验结果可以看出,SAS的预测结果与试验值也最为接近。相比较而言,WMLES方法的模拟结果整体上与试验值相差较大,特别是对间隙压强的预测。

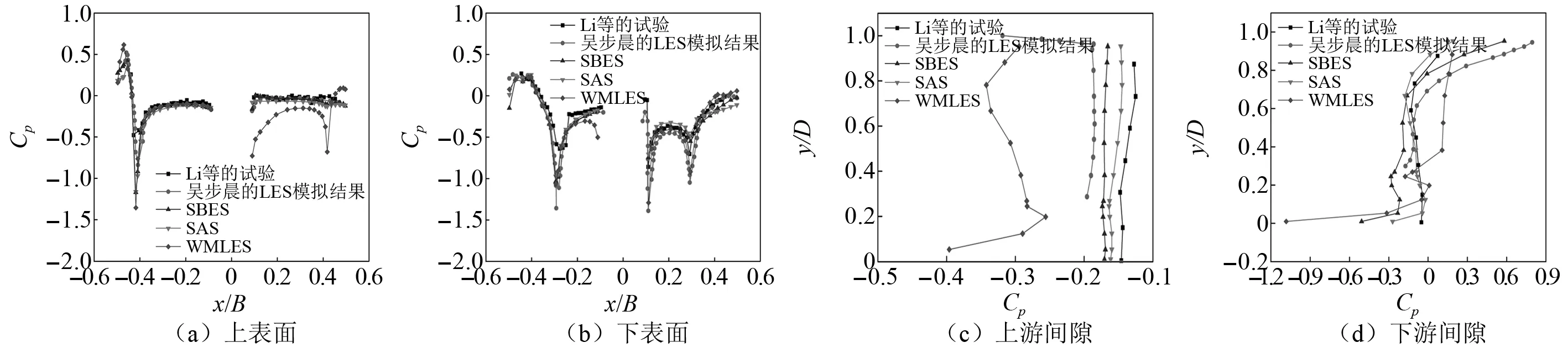
图10 分离式双箱梁平均压强系数分布图Fig.10 Distribution of mean pressure coefficients for the separated twin-box girder

图11 分离式双箱梁脉动压强均方根分布Fig.11 Distribution of the root mean square of the fluctuating pressure for the separated twin-box girder

Q准则显示的分离式双箱梁流场瞬时漩涡结构图,如图12所示。由图12可知,在断面周围、间隙中和断面尾部SBES方法同样展示出了非常丰富的三维漩涡结构。由于上游箱梁尾部具有显著的涡脱,SAS方法在间隙处成功捕捉到了三维的流动结构,随着漩涡在下游箱梁的附着,流动不稳定现象减弱,SAS方法的湍流黏性增大,抑制了小尺度涡的发展,最终在尾部仅有大尺度的漩涡结构。对于WMLES方法,上游箱梁的流动形态与流线型箱梁类似,都表现为近似的二维结构。下游箱梁的表面有较大的漩涡,同时尾部的涡脱也呈现三维特性,但由压强结果可知,WMLES方法对间隙和下游箱梁的流动形态预测是不准确的。

图12 分离式双箱梁瞬时漩涡截图Fig.12 Instantaneous vortex structures for the separated twin-box girder

综上分析可知,SBES方法无论是对流线型箱梁还是分离式双箱梁的气动力和三维流动结构都具有非常好的预测能力,相反WMLES方法由于采用了混合长度理论,并且在不同区域之间没有采用屏蔽函数,所以无法适用于流动分离存在的流场。SAS方法对于具有显著流动分离的流场具有较好的预测能力,比如钝体的双主梁断面、桥塔断面等,对于宽高比较大附着流占主导地位的结构,预测能力和URANS类似。

3.2 气动导纳识别

鉴于SBES方法对非定常气动力模拟的优秀表现,采用SBES方法对湍流来流下的箱梁断面气动力进行分析。网格1、网格2两种不同网格精度下箱梁断面在均匀来流下的平均压强系数,如图13所示。由图13可知,网格1和网格2的结果基本一致,并且与试验值吻合较好。压强系数的均方根值具有相同的特点,不再给出。考虑到计算效率,本文选取网格1作为计算网格。

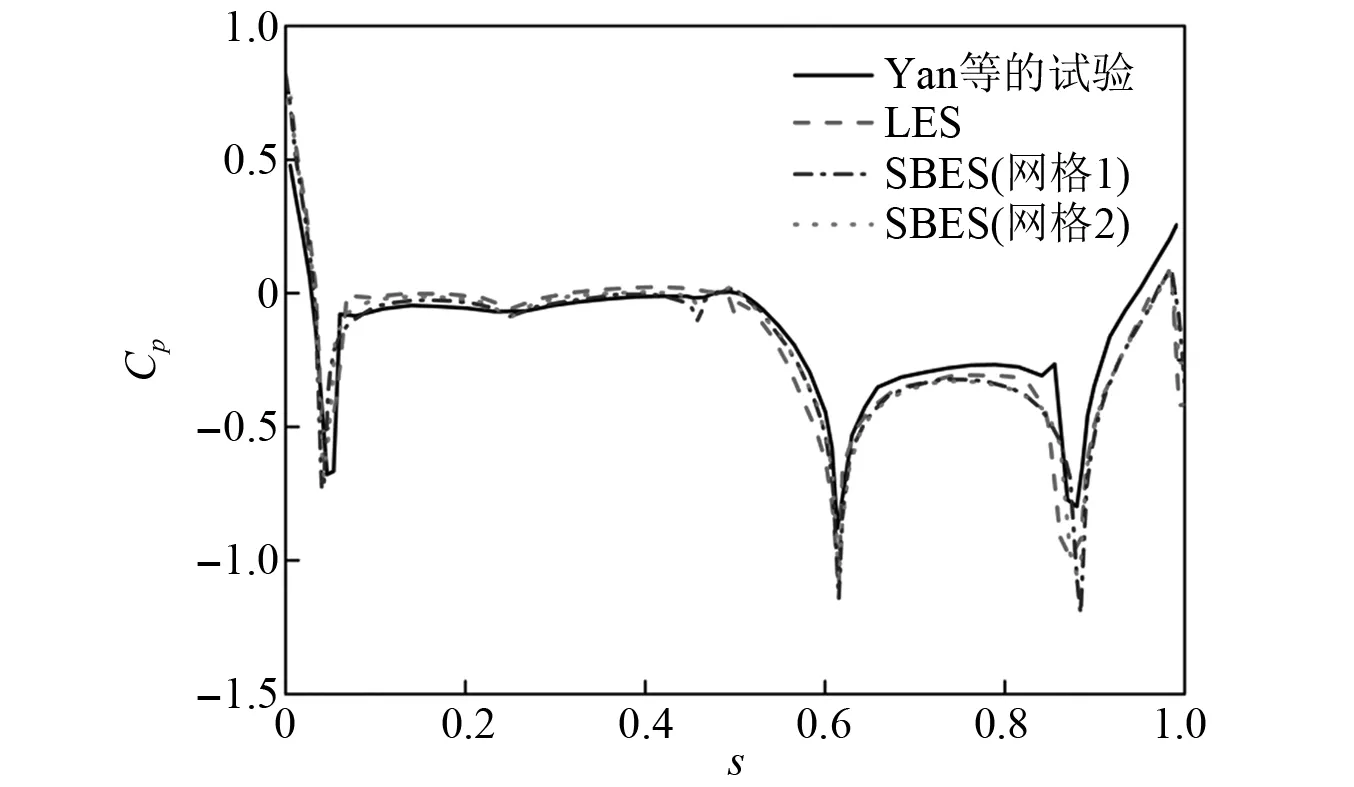
图13 不同网格精度下压强系数沿箱梁表面分布Fig.13 Mean pressure coefficient distribution of the box-girder section with different grid density

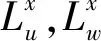
表2 来流湍流特性Tab.2 Turbulence characteristics of the incoming flow

图14 湍流来流下压强系数沿箱梁表面分布Fig.14 Pressure coefficient distribution of the box-girder section under turbulent flow

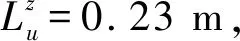
(14)

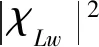
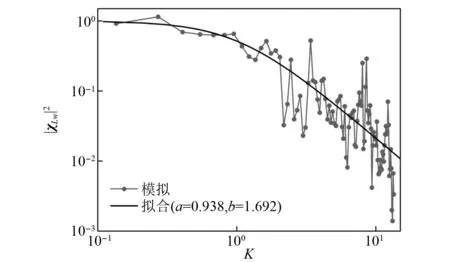
图15 气动导纳拟合结果Fig.15 Fitting of the aerodynamic admittance function

在两种风场中识别的升力气动导纳,如图16所示。图16同时给出了Sears函数和Yan等[32]的风洞试验结果。由图16可知,在K<3内,三者差别较大。具体表现为,小尺度湍流风场2中的结果与Sears函数基本一致,而大尺度湍流风场1中的结果明显大于Sears函数和风场2中的结果,这表明气动导纳随积分尺度的增大而增大,这与Larose等的研究结果一致。Yan等的试验结果与Sears函数的差别显著,数值远小于Sears函数,这种现象普遍存在于风洞试验中,主要是由于风洞试验中的湍流积分尺度偏小。相反,在折算频率K>3内,三者结果与Sears具有较好的一致性。

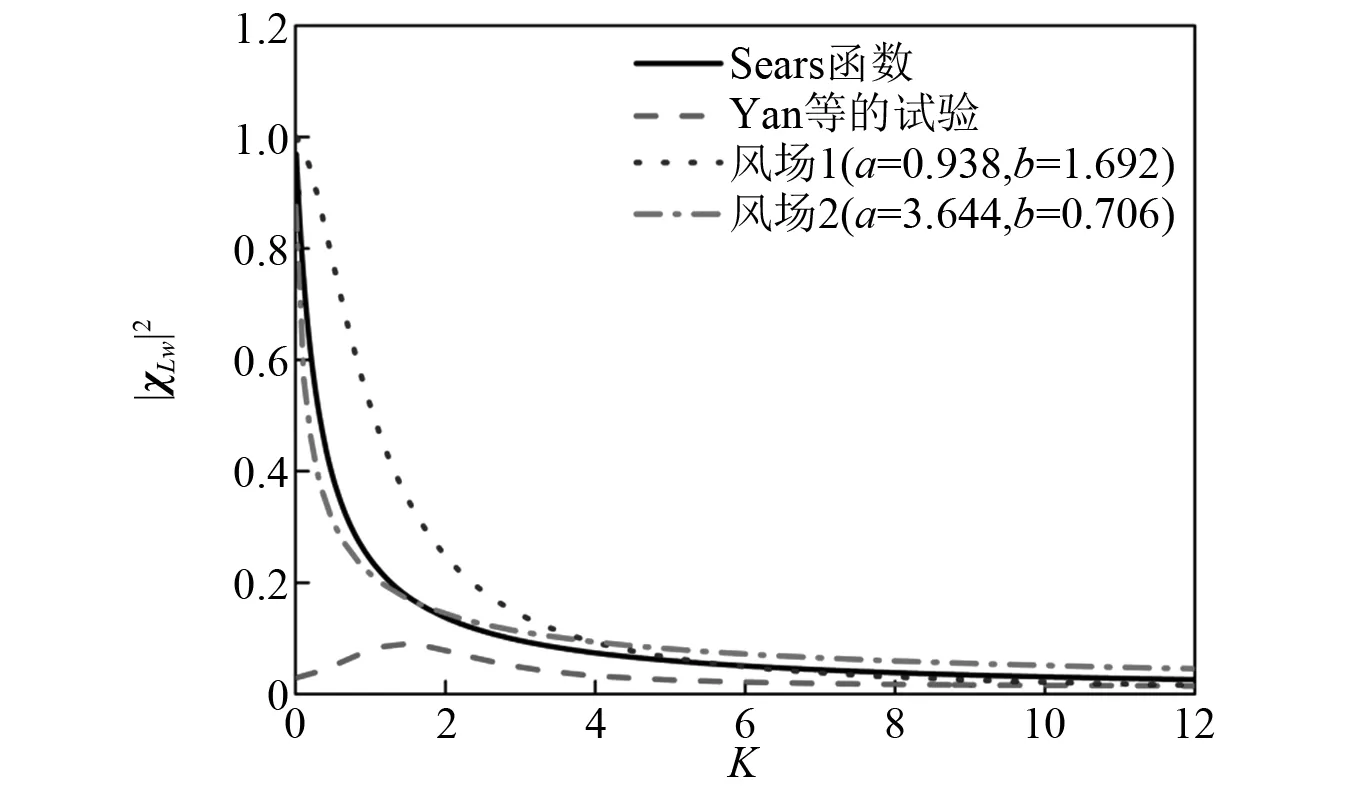
图16 不同流场中的气动导纳函数Fig.16 Aerodynamic admittance function in different turbulent flows

从本文大积分尺度下气动导纳的识别结果可以看出,积分尺度的增大会导致低频处气动导纳函数的增大。传统的利用格栅湍流节段模型测力风洞试验得到的结果,在数值上明显小于大积分尺度湍流下的结果,这意味着如果将小尺度格栅湍流场中识别的气动导纳用于实桥的抖振分析,必然会导致抖振力显著偏小。

4 结 论

RANS/LES混合方法,通过在边界层使用RANS在远离壁面区域使用LES,既避免了LES应用于桥梁风工程时所需的大量的计算代价,也能满足桥梁风工程对于静气动力和脉动气动力的需求。本文将RANS/LES混合方法和入口湍流合成方法相结合,实现了大积分尺度湍流场的数值模拟,并将此用于箱梁断面气动导纳的识别。本文主要的研究结论如下:

(1) 在以往人工合成湍流方法的基础上,本文通过引进时间尺度因子和与频率有关的积分尺度,使得合成的风速时程既满足无散度条件,又能正确模拟自然风的空间相关性和时间相关性。本文采用此方法,成功实现了大积分尺度湍流的人工模拟。

(2) SBES方法无论是对流动分离现象较弱的流线型箱梁还是存在气动干扰效应的分离式双箱梁,都能得到丰富的三维流动结构和准确的气动力。相比较而言,SAS方法对于具有显著流动分离的流场具有较好的预测能力,而WMLES方法整体表现都较差。

(3) 采用SBES方法分别在小尺度湍流和与实际风环境相似的大尺度湍流中,计算了一箱梁断面受到的非定常气动力,并识别得到了气动导纳函数。整体上,小尺度湍流场中的结果与Sears函数吻合较好,而大尺度湍流场中的结果在低频段明显大于Sears函数和小尺度湍流场中的结果,尤其与节段模型风洞试验的结果差距非常显著。

(4) 箱梁断面的升力气动导纳随积分尺度的增大而增大,这表明如果采用小尺度格栅湍流场中识别的气动导纳进行桥梁抖振分析,会导致低频处的抖振力小于实际值。