基于遗传算法的低振动噪声离心泵优化设计

韩志博 王玉勤 倪小强 胡 毅 周 生

（巢湖学院机械工程学院，安徽 巢湖 238000）

0 引言

本研究选取离心泵效率、扬程、轴功率这3 个目标函数，以对离心泵振动噪声影响较大的叶片数Z、叶轮出口直径D2、叶片出口安放角β2和叶轮出口宽度b2为变量，利用遗传算法对离心泵叶轮参数进行优化。

1 离心泵水力设计

选用IS80-65-160 型清水离心泵为原型泵，基本参数如下，流量Q=50 m3/h、扬程H=32 m、转速n=2 900 r/min。利用速度系数法对原型泵叶轮的主要结构参数进行设计［7］，结果见表1。

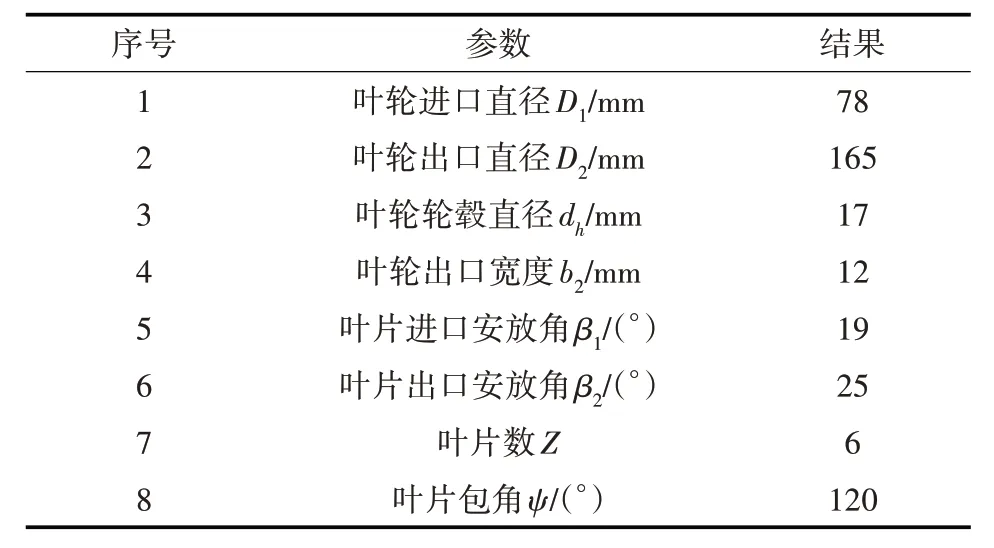
表1 原型泵叶轮的主要结构参数

2 建立目标函数

2.1 离心泵效率目标

离心泵在工作时会有能量损失，包括容积损失Pv、机械损失Pm和水力损失Ph，相关计算见式（1）到式（3）。

式中：ρ为液体的密度；g为重力加速度；Q为液体流量；Ht为理论扬程；u2为叶轮出口圆周速度。

根据斯托道拉公式得到离心泵的理论扬程，见式（4）、式（5）。

式中：u1为叶轮进口圆周速度；νu2为叶轮出口圆周分速度；νu1为叶轮进口圆周分速度。

假设不受叶片进口预旋的影响，即νu1= 0，理论扬程可简化为式（6）。

1)偏转角小于15°时，等效处理在30～100 m距离范围内对横向偏移的影响小于0.03 m，且对距离不敏感，并且横向偏移量偏差随偏转角度α增大而增大。

其中，νu2的计算见式（7）。

式中：σ为斯托道拉滑移系数。σ的计算见式（8）。

式中：ψ2为出口滑移系数，取ψ2= 0.85。

将式（7）带入到式（6）中，见式（9）。

综上所述，离心泵总效率的表示见式（10）。

离心泵最大效率目标函数见式（11）。

2.2 离心泵扬程和轴功率目标

离心泵扬程的表示见式（12）、式（13）。

式中：P1为进口压力；P2为出口压力。

离心泵所需的轴功率见式（14）。

离心泵最大扬程目标函数见式（15）。

离心泵最小轴功率目标函数见式（16）。

2.3 统一目标函数和约束条件

将式（11）、式（15）、式（16）整理得式（17）。

式中：ξi为分目标函数的加权系数。可将本优化过程简化为单一目标函数优化问题，结果见式（18）。

约束条件见式（19）。

3 遗传算法优化

利用Matlab 软件中的遗传算法工具箱来模拟生物进化的自然法则，输入上述统一目标函数，设定边界条件，输入变量，优化参数取值范围见表2。

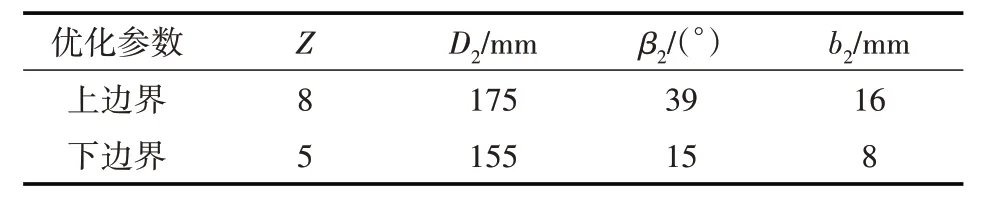
表2 优化参数取值范围

迭代优化结果见表3。

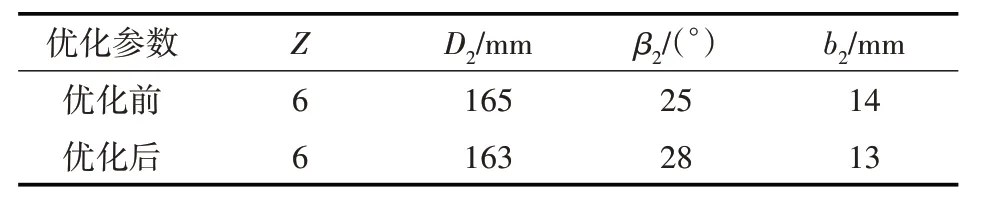
表3 优化结果对比

4 数值模拟

基于遗传算法优化结果，得到离心泵结构参数，利用CFturbo 软件对叶轮和蜗壳进行参数化建模，三维模型如图1所示。

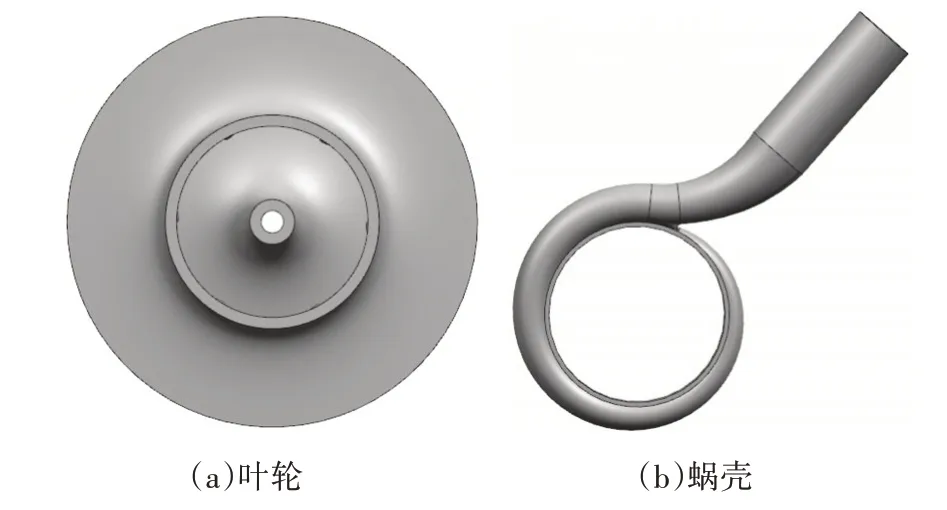
图1 离心泵三维模型

其对应的流体域模型如图2所示。

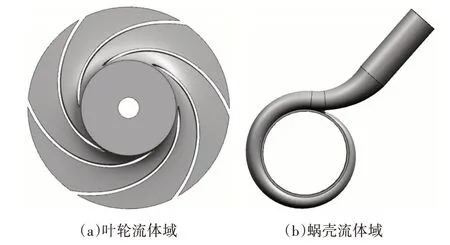
图2 离心泵流体域

利用ANSYS ICEM 软件对流体域进行网格划分，模型如图3所示。

图3 离心泵流体域网格模型

以非定常计算导出结果为基础，用ACTRAN 计算声学软件对离心泵内部声场进行数值模拟，研究离心泵内部噪声特性。改进后的泵与原型泵二阶叶频处外场流激噪声指向性分布如图4 所示。由图4 可知，改进后的泵的声压级比原型泵的声压级有明显下降。

图4 离心泵二阶叶频处外场流激噪声指向性分布

5 结语

以IS80-65-160 型离心泵为优化目标，当叶轮叶片个数为6、叶轮出口直径为163 mm、叶片出口安放角为23°、叶轮出口宽度13 mm 时，离心泵内部流动噪声较小。优化结果表明，遗传算法在离心泵振动噪声优化设计过程中具有一定的实用价值，优化后模型泵的流动噪声明显减弱，还能保证离心泵的效率、扬程和轴功率均在允许范围内。

本研究利用遗传算法对离心泵振动噪声进行优化设计，设计结果较为满意，但在此基础上，可结合更为先进的算法进行辅助验证，这是因为遗传算法的效率不高，比较容易进入早熟收敛状态，而多种算法结合验证得出相同设计结果，能有效提高设计的可靠性。同时，离心泵结构包括叶轮、蜗壳和主轴等，本研究主要考虑叶轮的性能，对离心泵整机性能还未进行深入研究，后续研究可将本研究的设计结果与离心泵其他过流部件进行深入融合，提升离心泵的整机设计性能。