素养立意的初中数学应用考查路径探析

林经武

摘 要：数学应用就是从现实世界中“抽象出”本质与内在规律，再对这些本质与规律进行量化与模型化.初中阶段关注的是应用意识的培养.素养立意的初中数学应用考查将关键能力、数学应用、数学探究等学科素养统一到代数思维这条主线上.

关键词：数学应用；数学素养；考查路径

《义务教育数学课程标准（2022年版）》在课程实施的评价建议环节中对学业水平考试的命题原则作了阐述：坚持素养立意，凸显育人导向.以核心素养为导向的考试命题，要关注数学的本质，关注通性通法，综合考查“四基”“四能”与核心素养.适当提高应用性、探究性和综合性试题的比例，题目设置要注重创设真实情境，提出有意义的问题，实现对核心素养导向的义务教育数学课程学业质量的全面考查.

1 数学应用的内涵外延

“应用”在《辞海》中的界定是“使用或实用”；在数学领域可理解为“抽象出”.美国学者D.A.格劳斯（Grouws）认为，“数学应用”就是从现实世界中“抽象出”本质与内在规律；应用数学家波拉克（Henry Pollak）提出：“要用数学的观点看世界”，即对现实世界的量化与模型化；我国学者任子朝、赵轩认为“数学应用”培养学生能自觉地从数学的角度观察、理解、思考现实问题，能运用数学知识解决实际生活中的问题.这里的“看”“观察”等行为动词就是“抽象出”的表征.

初中阶段对数学应用更多关注的是数学模型观念和应用意识的培养.模型观念主要是指对运用数学模型解决实际问题有清晰的认识，从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果并讨论结果的意义.应用意识主要是指有意识地利用数学的概念、原理和方法解释现实世界中的现象与规律，解决现实世界中的问题.

数学应用的内涵就是对一些本质与规律进行量化与模型化，对于它的外延可以是各种数学内部的公理化或理论化体系（纯数学）的理论研究，也可以是对现实世界中具有一定规律或性质的现象研究.

2 数学应用的考查路径

初中数学试题命制需将学科素养统一到理性思维这条主线上，因为理性思维在数学素养中起着最本质、最核心的作用.因此素养立意的初中数学应用考查是有意义的，可触摸的，只要立足运算能力、几何直观、推理能力、模型概念等关键能力，考查必然统一到代数思维这条主线上，所以数学应用的考查路径是可视的、可操作的.

2.1 利用生活实践情境，考查模型观念

从“生活实践情境”入手，考查学生运用所学知识解释生活中的现象、解决生产实践中的问题的能力.关注数学模型的抽象、建模、解模、验模的过程，在操作的层面上：问题抽象时要引入需要的参数，建立多元表征，在这个过程中对字母意义的理解是关键；建模时会抓住核心变量、变量的规律及变量之间的关系，能从表象到本质，从具象到一般，找到可以表征的模型；解模时会找到原理和方法，将概念和定理具体化并用于相应的场景与情境；验模即会有效监控自己的思维过程，对自己的问题解决过程有评价与反思的意识.这类数学应用的考查路径以“抽象—建模—解模—验模”为抓手，关联方程、不等式或函数等必备知识，立足数学阅读、运算能力、推理能力、模型观念等关键能力，培育代数思维，发展模型观念.

案例1：（2022年厦门市质量抽测第21题）

某旅游区的湖边有一个观赏湖中音乐喷泉的区域，该区域沿湖边有一条东西向的长为32 m的栏杆.考虑到观景安全和效果，旅游区计划设置一个矩形观众席，该观众席一边靠栏杆，另三边用现有的总长为60 m的移动围栏围成，并在观众席内按行、列（东西向为行，南北向为列）摆放单人座椅，要求每个座位占地面积为1 m²，且观众席内的区域恰好都安排了座位.

（1） 若观众席内有x行座椅，用含x的代数式表示每行的座椅数，并求x的最小值；

（2） 旅游区库存的500张座椅是否够用？请说明理由.

评析：命题者以“音乐喷泉的观众席”为问题情境，在知识领域上考查一元一次不等式、二次函数的相关知识；在思想方法上考查函数与方程思想、数形结合思想、配方法；在学科素养上考查运算能力、应用意识、模型观念.

试题解答：

（1） 解：每行的座椅数为：60-2x.

因为栏杆总长为32 m，且每个座位为占地面积1 m²的正方形，所以60-2x≤32，解得x≥14，所以x的最小值为14.

（2） 解：设观众席内的座位数为y，

由题得y＝x（60-2x），其中14≤x＜30，其中x为整数，所以y＝-2x²+60 x＝-2（x-15）²+450，所以y的最大值为450.

因为450＜500，所以库存的500张座椅够用.

答：旅游区库存的500张座椅够用.

思考：我们知道用数学方法解决任何一个实际问题，都必须在实际问题与数學知识之间架设一座“桥梁”，这“桥梁”就是模型的搭建.本题的设置就是让学生找到恰当的“桥梁”，通过合理的抽象，用“定量化”的语言（如不等式）或结构（如二次函数模型）来描述现象中的内在规律并能用这语言与结构解释.

案例2：（2022年福州市九年级第一学期期末质量抽测第9题）我国南宋数学家杨辉在《田亩比类乘除捷法》中记录了这样的一个问题：“直田积八百六十四步，只云长阔共六十步，问长多阔几何？”其大意是：矩形面积是864平方步，其中长与宽和为60步，问长比宽多多少步？若设长比宽多x步，则下列符合题意的方程是（    ）.

A. （60-x）x=864

B. （60-x/2）·（60+x/2）=864

C. （60+x）x=864

D. （30+x）（30-x）=864

评析：本题让学生用数学的眼光观察世界，关注数学应用的任务情境——文化自信：感受数学文化，感受数学之美.让学生经历“抽象——建模——解模——验模”的过程，如在问题解决过程中学生应明确该模型中的变量是长与宽的差值，不变量是矩形的面积.学会用题目已设字母来表征矩形中的长和宽，感悟代数思维带来解题的顺畅感和成就感.

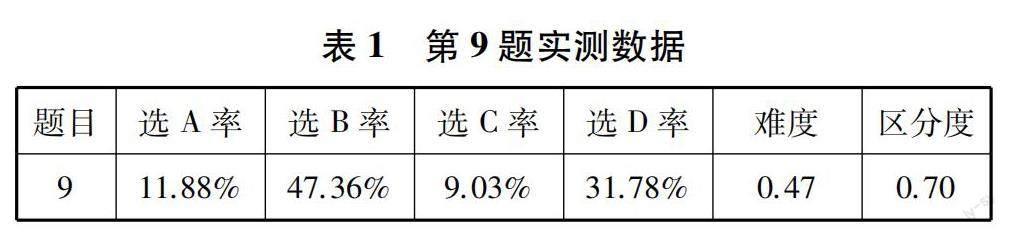
从表1可以看到，不同素养水平上的学生在这些任务情境中的表现不一样，正确率不到50%，难度0.47，区分度0.70，这是一道区分度很好的试题.考查学生数学代数思维，发展模型观念和应用意识.

2.2 利用学习探索情境，考查应用意识

从“学习探索情境”入手，考查学生在真实的研究过程或实际的探索过程中，运用数学知识与方法发现、提出、分析和解决问题的能力，涵盖学习探索与科学探究过程中所涉及的问题.学生在解决这类情境中的问题时，必须启动已有知识开展智力活动，同时在解决问题的过程中运用创新的思维方式，综合运用所学知识达到问题解决的目的.这个过程中要关注字母的意义与参数引入的必要性；关注情境下模型的建立、求解并解释的能力.这类数学应用的考查路径以“过程和结构”为抓手，找出試题中的未知结果与已知信息之间存在的关系，且把这种关系表征出来，同样关联必备知识，立足关键能力，培育代数思维，发展模型观念.

案例3：（2022年武汉中考第10题）

幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，例如图（1）就是一个幻方.图（2）是一个未完成的幻方，则x与y的和是（    ）.

A. 9

B. 10

C. 11

D. 12

评析：试题考查学生对九宫格的信息提取，借助题目中“每一横行、每一竖列以及两条对角线上的3个数之和相等”，找出图（2）中第一列和第一行有公共的数x，这公共数是隐藏的，无需求出，得出左下角的数是4，以此类推.而这些公共的数（同一量）都可以用不同的方式表达，而一切存在等量关系的求值问题本质上都是方程的问题，这便是试题命制要考查学生从数学问题的内部抽象出的方程模型.这道试题从题面上看情境简单，条件明确.但是如何从传统应用问题中直接告知的等量关系的寻找，迁移到表格功能性作用下抽象出方程的模型是问题解决的关键.学生由于除对情境中“九宫格的信息的提取”不熟悉外，还对题目中“每一横行、每一竖列以及两条对角线上的3个数之和相等”这一条件的运用没有找到合适的切入点，导致失分.这道试题经过实测算是选拔性很高的试题.

案例4：（2022年福建中考第23题）

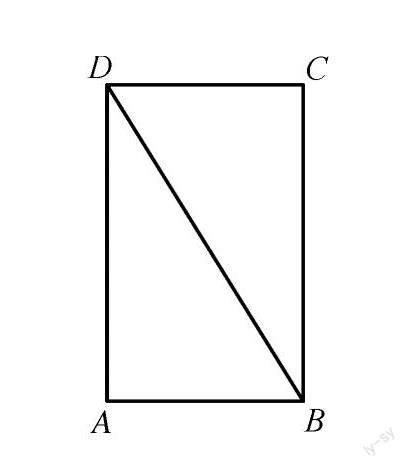
如图，BD是矩形ABCD的对角线.

（1） 求作⊙A，使得⊙A与BD相切（要求：尺规作图，不写作法，保留作图痕迹）；

（2） 在（1）的条件下，设BD与⊙A相切于点E，CF⊥BD，垂足为F.若直线CF与⊙A相切于点G，求tan ∠ADB的值.

评析：本题第（1）问略；第（2）问解决的最佳路径是“几何问题代数解决”，以“过程和结构”做抓手，探究本题所求“tan ∠ADB的值”与依据已知条件所呈现出来图形中的边、角等基本元素之间存在的关系：位置关系在前、数量关系在后，数量化的几何变换在图形中的解决，且把这种关系用符号或者由符号组成的代数式或方程表征出来，关联矩形、圆、圆的切线等必备知识，立足数学阅读、识图画图、推理能力、运算能力等关键能力，培育代数思维，发展模型观念.

上述呈现的四种解法中，无论哪种解法，思维过程都经历“设未知数——量的表征——呈现结果”，这是代数思维的常见逻辑，代数代表更多的普遍性和一般性（如运算律与公式）；代表着一种思维逻辑（字母与数一样可以参与运算）；表现的是一种思维方式（已知与未知的同等地位作用），也是命题者对“学习探索情境”这类数学应用的常见命题理念.因此试题命制在一定程度上引领教学导向，数学应用教学最终走向培育代数思维，发展学科核心素养.

3 结束语

无论“利用生活实践情境，考查模型观念”的试题命制还是“利用学习探索情境，考查应用意识”的试题命制，都在引领教师关注教学，关注学生数学学习的过程，关注对数学课程本质的整体把握、数学理解的拓展.对于教材中数学应用问题，关注字母的引入和使用，关注数学模型的抽象、建模、解模、验模的过程，关注代数思维的建立与培养，则是意在真正让学生做到探中学，学中会、会中用.

参考文献：

［1］ 义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

［2］ 教育部教育考试院.深化高考内容改革，加强教考衔接［J］.中国考试，2022（7）：16.

［3］ D.A.格劳斯.数学教与学研究手册［M］.上海：上海教育出版社，1999.

［4］ 任子朝，赵轩.基于高考评价体系的数学科考试内容改革实施路径［J］.中国考试，2019（12）：2732.

［5］ 陈昂，任子朝.数学高考中实践应用能力考查研究［J］.数学教育学报，2017（3）：1518.

［6］ 喻平.数学关键能力测验试题编制：理论与方法［J］.数学通报，2019（12）：17.

［7］ 王秀秀，董磊，陈棉驹.初中数学模型思想方法的内涵及教学分析［J］.中学数学教学参考：上旬，2019（11）：6265.

［8］ 鲍建生，等.数学学习的心理基础过程［M］.上海：上海教育出版社，2009.

［9］ 柯跃海.选拔性数学考试的命题与评价［M］.西安：陕西师范大学出版社，2018.