基于轴承和柔性铰链的布拉格光纤光栅加速度计

宋 颖，张浩然，李剑芝，申博豪，刘占剑

（1.石家庄铁道大学 河北省交通安全与控制重点实验室, 河北 石家庄 050043；2.石家庄铁道大学 交通运输学院, 河北 石家庄 050043；3.石家庄铁道大学 河北省大型结构健康诊断与控制实验室, 河北 石家庄 050043；4.石家庄铁道大学 机械工程学院, 河北 石家庄 050043；5.石家庄铁道大学 材料科学与工程学院, 河北 石家庄 050043）

1 引 言

中高频振动信号的精确测量已成为国内外的研究热点[1-2]。其对如高速动车组轴箱振动、微地震等许多工程监测具有重要意义[3-4]。传统电类传感器易受电磁干扰，而且导线过长等会造成信号衰减，特殊环境应用困难[5]。光纤布拉格光栅（Fiber Bragg Grating，FBG）加速度传感器采用无源传感元件，光信号传输不受电磁和距离等因素影响，而且耐腐蚀、可组网、易于实现分布式传感[6]，适用于恶劣环境下的振动监测，引起了科研人员的广泛关注。

FBG 加速度传感器为波长调制型光纤传感器，主要有悬臂梁式、圆形膜片式、柔性铰链式以及其它一些特殊结构。它们的传感原理是通过质量块带动光纤光栅使之产生轴向应变，导致波长发生变化，然后通过FBG 波长变化来获得加速度。其中悬臂梁式结构[7-10]研究较早，理论推导简便，具有结构简单的显著优势；圆形膜片结构[11-13]由于质量块横向位移被限制，具有横向干扰小的显著特点。但上述两种结构受本身刚度限制，测量中高频振动时灵敏度过低。例如，LI T L[11]设计了一种圆形膜片结构的传感器，固有频率为600 Hz，灵敏度为20.189 pm/g；WU H[14]设计了一种基于变厚度双悬臂梁结构的FBG 传感器，固有频率达8 658 Hz，灵敏度仅0.44 pm/g。此外，其他特殊结构的FBG 加速度传感器的灵敏度也较低，例如WANG[15]设计的基于钢管和双FBG 的FBG加速度传感器，固有频率达到3 806 Hz，但其灵敏度仅为4.01 pm/g。柔性铰链结构[16-18]具有较宽的测量频率范围，采用柔性铰链结构后，灵敏度可得到一定的提高，但提升效果有限。例如，LIANG L[17]等人设计了一种单铰链结构传感器，固有频率为900 Hz，灵敏度为26.962 pm/g。为了进一步提高灵敏度，LUO X D[19]、QIU ZH CH[20]等采用对称柔性铰链结构和双质量块增大FBG 轴向应变，固有频率分别为890 Hz 和1 300 Hz，灵敏度分别可达到41 pm/g 和20 pm/g。LI Z CH[21]等人设计了一种三柔性铰链结构，固有频率为2 800 Hz，灵敏度达21.8 pm/g。多柔性铰链结构会引起回转精度误差叠加[22]，导致传感器线性度下降。

综上所述，目前采用单质量块和单柔性铰链结构的FBG 加速度传感器，灵敏度偏低。而采用双质量块和多铰链结构虽可增加灵敏度，但将导致线性度下降。针对上述问题，本文提出一种中间为单柔性铰链、两侧为轴承支撑结构的对称式FBG 加速度传感器。该结构不仅能提高测量频率范围，还具有较高灵敏度，可实现中高频振动信号的精确测量。

2 传感器设计

根据工程结构中高频振动信号的测量需求，设计了一种柔性铰链连接、两侧轴承支承的对称式双质量块FBG 加速度传感器，如图1 所示，包括2 个质量块、2 个轴承、1 个柔性铰链、2 根光纤光栅（FBG1和FBG2）以及基座。两轴承和两质量块呈对称布置，中间仅用一个柔性铰链连接。轴承外圈固定在两质量块外侧突起的连接臂上，质量块可绕轴承中心轴微转动。采用两点封装方式将两根光纤光栅分别粘贴在质量块上下延伸杆末端并施加一定预应力，避免产生啁啾效应。通过改变柔性铰链的最小厚度，还可以调整频率测量范围和传感器灵敏度，以适应不同的应用环境。当FBG 加速度传感器受到外界振动激励时，两质量块同时绕轴承中心转动，两根光纤光栅产生轴向应变进而引起光栅波长变化，根据振动加速度与光栅波长之间的数学关系即可获得待测加速度信息。

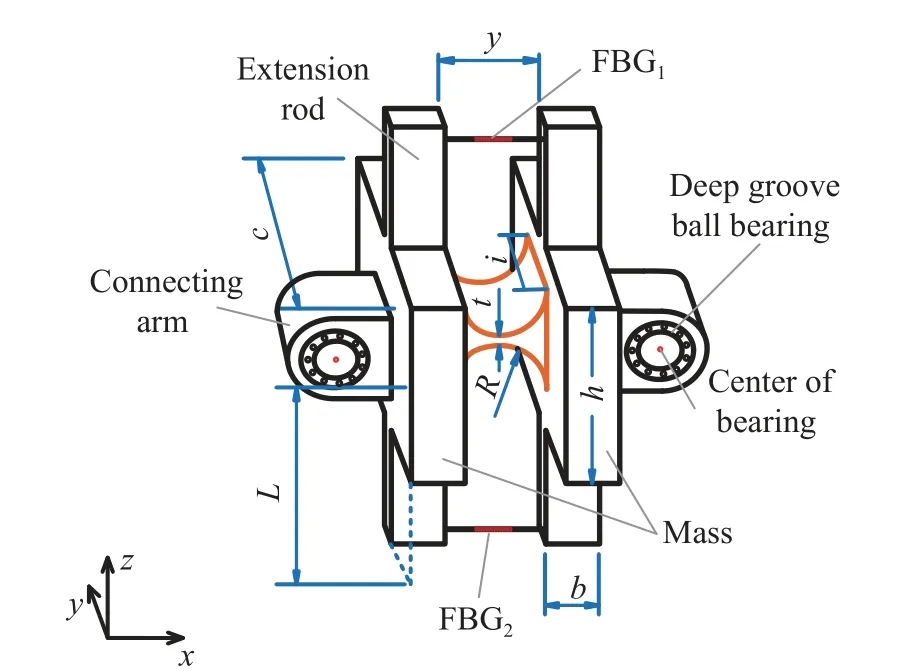
图1 FBG 传感器结构示意图Fig.1 Schematic diagram of the FBG structure

设计的传感器采用单柔性铰链连接两质量块，并增加了轴承结构，既可提高传感器灵敏度，又可避免多铰链结构产生的传感器线性度和量程减小的问题，同时质量块在低阶模态不会产生同向转动，保证传感器具有较宽的频率测量范围。另一方面，采用双光栅结构，两根光栅轴向应变方向相反，这种既提高了灵敏度又消除了温度影响。

3 理论分析

所设计的FBG 加速度传感器采用对称双光栅结构，其中心波长同时受轴向应变和温度影响

式中， ∆λ1、 ∆λ2分别为FBG1和FBG2的波长变化量；Pe为有效弹光系数；ε1、 ε2分别为FBG1和FBG2应变； λ1、 λ2分别为FBG1和FBG2的中心波长；αf为光纤热膨胀系数； ξ为光纤材料热光系数；∆T为温度变化量。

当质量块受到外界振动导致两根光栅FBG1和FBG2出现变形时，其中一个受拉，另一个受压，其波长变化量大小相等，方向相反，即ε1=|-ε2|=ε 。 两光栅中心波长值相近，即 λ1≈λ2=λ，总波长变化量可以表示为

利用公式(3)既可以消除公式(1)和公式(2)中的温度项，实现温度补偿，又可以使波长变化量提高一倍。

理论公式推导时忽略阻尼，当质量块受到垂直振动加速度a激励时，根据牛顿第二定律和胡克定律有

式中，K为系统刚度，xm为质量块位移，Me为系统等效质量。

当加速度方向向上时，由于惯性，质量块相对于轴承向下转动，根据力矩平衡，质量块转动角度为 θ时，质量块受到柔性铰链竖直方向的弹力Fh和光纤传递到质心竖直方向的拉力Ff而发生转动，如图2 所示。由于转动角度很小，将Fh和Ff视为竖直方向的力，其合力为F。

图2 工作原理示意图Fig.2 Diagram of the working principle

两质量块对称布置，以图2 左侧质量块为例，其位移与FBG1拉伸长度分别近似为

式中，s=R/t；E为材料弹性模量；R为直圆型柔性铰链切割半径；t为最小厚度；i为柔性铰链深度；Ef为光纤弹性模量；Af为光纤横截面积；y为光纤长度，即两质量块间距。

根据力矩平衡，有

所设计FBG 加速度传感器总灵敏度为FBG1和FBG2的叠加，即2S。由式(14)和式(17)可以看出，FBG 加速传感器固有频率f和灵敏度S互相限制，即提高f或S将导致另一参量降低。

4 优化设计与仿真分析

4.1 结构优化设计

通过理论分析发现，对传感器固有频率和灵敏度影响较大的结构参数有：光纤有效长度y，柔性铰链半径R、最小厚度t、深度i，质量块长b、宽c、高h，以及左侧质量块质心到光纤粘贴点之间的垂直距离L。上述参数对FBG 加速度传感器固有频率和灵敏度的影响如图3 所示。可以看出除了光纤有效长度y之外，固有频率和灵敏度均随各结构参数值增大呈反方向变化，即固有频率与灵敏度互相限制。

图3 FBG 加速度传感器结构参数对固有频率和灵敏度的影响Fig.3 The influence of structural parameters of FBG accelerometer on natural frequency and sensitivity

为了满足中高频振动测试需求，所设计FBG加速度传感器应同时具有较宽工作频率范围和较高灵敏度。由图3(a)可知，固有频率和灵敏度随着光纤有效长度y的增加而减小，由于光纤光栅长度限制，选择y= 5 mm。对于柔性铰链，其参数取值主要影响系统刚度和固有频率。由于两质量块之间的宽度与光纤光栅的有效长度相等，柔性铰链半径R即为两质量块之间宽度的一半，R=2.5 mm。由图3(b)可知，传感器固有频率随柔性铰链厚度t的增大而增大，但当t/R>0.85 时，柔性铰链刚度模型误差较大，当0.2535 mm 时，固有频率随着L的增加，快速减小，灵敏度也开始缓慢减小。为了保证传感器兼具较高的频率测量范围和较高灵敏度，取L= 20 mm。综上所述，中高频FBG 加速度传感器结构参数如表1 所示，理论固有频率为3 667.7 Hz，单栅灵敏度为16.10 pm/g。

表1 加速度传感器尺寸参数Tab.1 Dimensional parameters of FBG accelerometer

4.2 数值仿真分析

为了验证所设计FBG 加速度传感器的动态特性，建立基于COMSOL 的传感器有限元仿真模型。将质量块、连接臂、延伸杆、柔性铰链视为一体结构，材料为304 不锈钢，密度为7 850 kg·m-3，弹性模量为210 GPa。光纤光栅材料为二氧化硅，采用二氧化硅圆柱体模拟光纤光栅，密度为2 500 kg·m-3，弹性模量为72 GPa。然后，基于该模型进行FBG 加速度传感器频响特性和瞬态特性分析，得到传感器固有频率仿真值为3 810.7 Hz，如图4 所示。工作频率平坦区为0～1 200 Hz，如图5 所示。施加频率为500 Hz，幅值分别为10 g、20 g、30 g 的正弦激励，得到FBG 加速度传感器在500 Hz 激振频率下的光纤光栅波长变化量随振动加速度的变化，如图6 (彩图见期刊电子版)所示。根据灵敏度计算公式得出传感器灵敏度为11.89 pm/g，与理论计算值16.1 pm/g 之间存在一定误差。其原因在于当柔性铰链取值确定且t/R=0.8 时，柔性铰链刚度模型存在误差[23-24]，因此仿真灵敏度比理论灵敏度小，出现了约20%的误差。

图4 传感器一阶振型图Fig.4 Characteristic frequency of sensor

图5 频响特性曲线仿真结果Fig.5 Simulation results of frequency response characteristics

图6 正弦激励下光纤光栅波长变化量(500 Hz)Fig.6 Wavelength shift of FBG under different sinusoidal excitations (500 Hz)

5 实验研究

为了获得该传感器的工作频率范围和灵敏度，在理论推导和数值仿真的基础上，进行了FBG加速度传感器动态特性实验，包括幅频特性实验、幅值特性实验、重复性实验、抗横向干扰实验等。

FBG 加速度传感器动态测试实验系统原理图如图7 所示，将FBG 加速度传感器固定在振动台上，然后连接至光纤光栅解调仪，通过笔记本电脑记录FBG 波长。其中，振动台采用IPA60H/M544A电动振动试验系统；额定频率为2～2 700 Hz，额定加速度为981 m/s2；采用Gator 高速光纤光栅解调仪，波长为1 516～1 584 nm，波长稳定性为5 pm，采样频率为10 kHz。实验中采用标准压电式加速度计获取振动加速度信号，试验现场如图8 所示。

图7 FBG 加速度传感器动态测试原理图Fig.7 Schematic diagram of dynamic test for FBG accelerometer

图8 试验现场及传感器实物图Fig.8 Physical sensor and experimental site

5.1 幅频特性分析

为了确定所设计的FBG 加速度传感器的工作频率范围，进行了幅频特性实验。实验中，先将振动台加速度大小固定为10 g，采用标准压电加速度计测试加速度值作为参考；然后对FBG 加速度传感器进行扫频测试，激振频率分别为10 Hz、150～1 800 Hz（步长150 Hz）、2000～2 300 Hz（步长100 Hz）及2 500、3 000、4 000、5 000 Hz，每次振动持续时间30 s，通过Gator 光纤光栅解调仪记录波长变化，最后获得传感器的幅频响应曲线，如图9 所示。从图中可以看到频率响应范围平坦区为10～1 200 Hz，共振频率为2 200 Hz，与无阻尼固有频率3 667.7 Hz 之间的差距主要是振动系统阻尼所致，所设计传感器阻尼比约为0.8，满足传感器阻尼比的设计要求[25-26]。

图9 幅频特性曲线Fig.9 Amplitude frequency characteristic curve

5.2 幅值特性分析

FBG 加速度传感器灵敏度用于描述被测振动加速度与FBG 总波长变化之间的数学关系。实验中，分别对振动台施加频率为100、300、600 和1 000 Hz 的振动加速度信号，加速度变化范围为2～40 g，步长增加间隔为4 g，受振动台功率限制，1 000 Hz 激振频率下的加速度最大为30 g。得到的FBG 加速度传感器单栅灵敏度和总灵敏度响应曲线分别如图10～图11 所示。可见：FBG 波长漂移量与加速度大小具有良好的线性关系，波长随着振动加速度的增大而线性增大；振动频率分别为100、300、600、1 000 Hz 时，FBG1灵敏度标定曲线斜率分别为10.42、10.17、10.33、13.12，平均值为11.01；FBG2的灵敏度标定曲线斜率分别为5.89、5.15、6.29、7.65，平均值为6.25。如图11所示，FBG 加速度传感器的总灵敏度标定曲线斜率分别为16.31、15.31、16.61、20.77，平均值为17.25。各灵敏度标定曲线线性拟合度均大于0.99，线性度良好。综上所述，FBG1的标定灵敏度为11.01 pm/g，FBG2的标定灵敏度为6.25 pm/g，传感器总灵敏度为17.25 pm/g。由于柔性铰链刚度模型存在误差，FBG1单栅实测灵敏度较理论值略低，但与有限元仿真分析灵敏度（11.89 pm/g）基本一致。同时，由于手工封装存在误差，改变了FBG2的有效光纤长度y。根据图3（a）中灵敏度S随有效光纤长度y的变化规律，FBG2的有效光纤长度y增大导致其灵敏度与理论值相比偏小。

图10 不同振动加速度信号下FBG1、FBG2 灵敏度标定曲线。（a）100 Hz；（b）300 Hz；（c）600 Hz；（d）1 000 HzFig.10 Sensitivity calibration curves at different vibration acceleration signals.(a) 100 Hz; (b) 300 Hz;(c) 600 Hz; (d)1 000 Hz

图11 FBG 加速度传感器总灵敏度标定曲线Fig.11 Total sensitivity calibration curves of FBG acceleration sensor

对振动台施加1 000 Hz，2～30 g 的振动激励，重复测量3 次，获得的光纤光栅波长变化量数据如表2 所示，计算得到的重复性误差为2.33%，重复性良好。

表2 不同加速度下光栅波长变化量Tab.2 Wavelength shifts of FBG at different accelerations

图12（彩图见期刊电子版）为不同激振频率下FBG 加速度传感器的波长变化时程图，其中图12(a)～12(b)振动频率分别为100、300 Hz，加速度大小为40 g，图12(c)～(d)振动频率分别为600 Hz、1 200 Hz，加速度大小为10 g。由图12可知，FBG 加速度传感器能够很好获取外界输入的正弦激励，正弦波形完好表明FBG 受力均匀，无啁啾与多峰现象。此外，同一时刻光栅FBG1输出波长曲线的波峰对应FBG2输出波长曲线的波谷，输出正弦波长相位差为180°，可提高传感器测试灵敏度。

图12 不同频率、加速度下FBG 波长时程图。（a）100 Hz，40 g；（b）300 Hz，40 g；（c）600 Hz，10 g；（d）1 200 Hz，10 gFig.12 Time history curves of FBG wavelength caused by different vibration acceleration signals.(a) 100 Hz, 40 g;(b) 300 Hz, 40 g; (c) 600 Hz, 10 g; (d)1 200 Hz, 10 g

图13 为各频率振动激励下的FBG 加速度传感器光栅波长频谱分析图。图13(a)、13(b)为100 Hz 和300 Hz 激振频率下的光栅波长频谱分析图。从图中可看出：除了振动台激振频率外，还有一个振幅较大，频率约为2 000 Hz 的振动信号。通过与未施加振动激励时FBG 加速度传感器光栅波长频谱图（图13(c)）进行对比，发现也存在频率约为2 000 Hz 的振动信号。此外，与传感器未安装在振动台上时的光栅波长频谱图（图13(d)）进行对比，发现未出现此频率的振动信号。因此推断2 000 Hz 振动信号为振动台自身的振动。

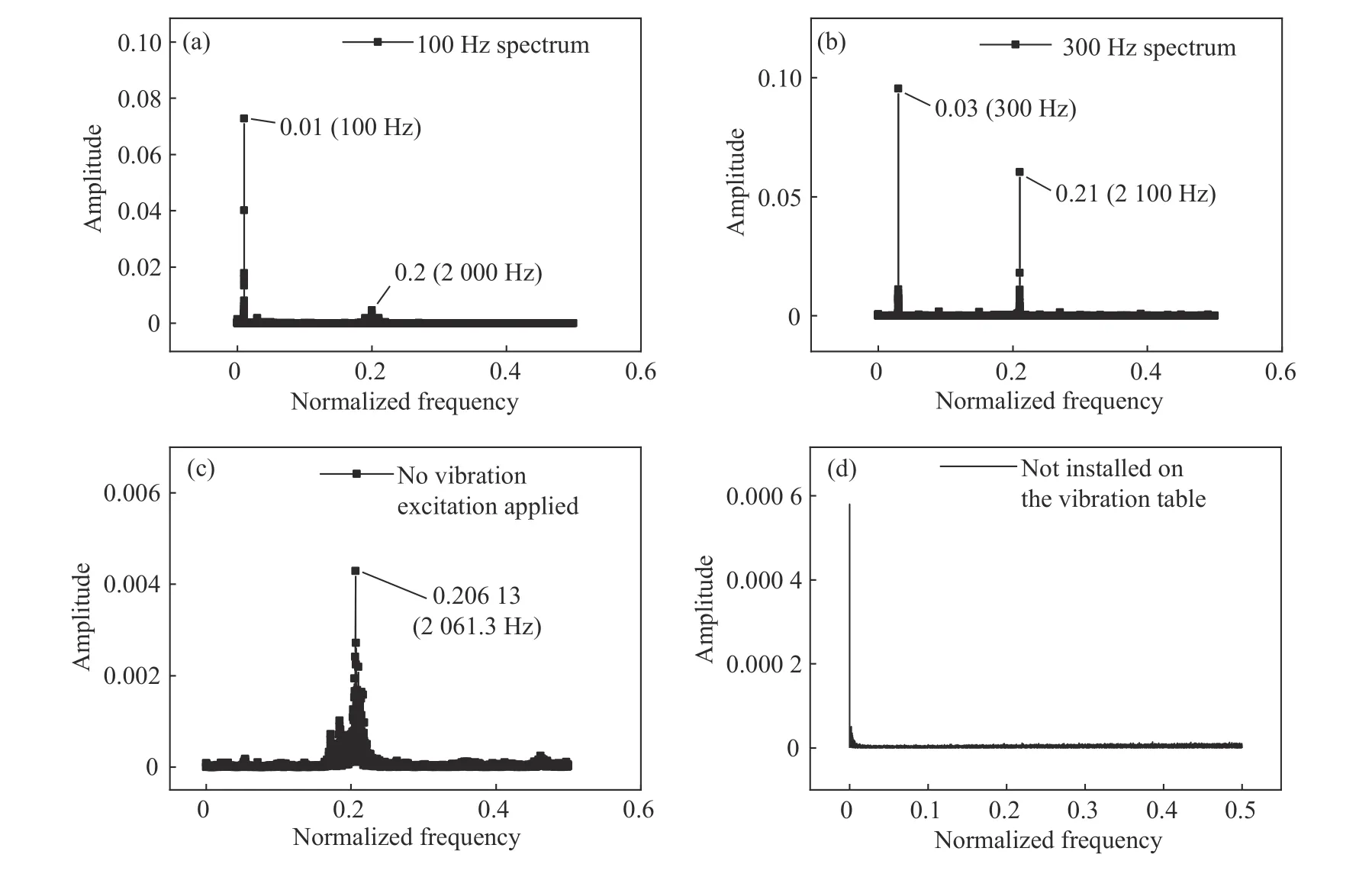
图13 不同频率振动激励下FBG 波长变化频谱图Fig.13 FBG wavelength spectrogram under different frequency vibration excitations

5.3 横向灵敏度分析

横向灵敏度比值是衡量加速度传感器质量优劣的重要指标，通常以轴向灵敏度的百分数来表示，如式(19)所示。实际应用环境中，振动可能来自多个方向，信号成分复杂。为了提高测量精度，需要保证传感器不受其他方向振动信号的干扰。横向灵敏度比值一般表示为

式中，Sr为横向灵敏度比值；St为横向灵敏度；Sl为轴向灵敏度。

在横向抗干扰实验中，设置振动台振动方向垂直于其测振主轴方向，激振信号为22 g，频率为1 000 Hz，同时记录FBG 波长。图14 是振动方向为横轴与主轴方向时FBG 加速度传感器输出波长时程对比图。由图14 可知，横向放置FBG加速度传感器时FBG1波长变化量为40.51 pm；竖向放置FBG 加速度传感器时FBG1波长变化量为283.45 pm，横向灵敏度比值为14.29 %。产生横向干扰的原因主要是质量块绕z轴转动引起光纤光栅x方向的轴向变形。这是由于轴承存在间隙，无法提供足够的横向刚度，使质量块在受到横向振动时产生横向位移。为了减小横向干扰，应在保证z 轴方向刚度不改变的前提下，尽量增大y轴方向的刚度。

图14 FBG 加速度传感器横向灵敏度Fig.14 Transverse sensitivity curves of FBG acceleration sensor

本文设计的传感器与现有FBG 加速度传感器的结构与性能对比如表3 所示。从表中可以看出，现有中高频加速度传感器多采用钢管、双质量块和双铰链或多铰链等弹性元件，而本文采用轴承、双质量块和单柔性铰链结构，避免了多铰链回转精度低而导致的传感器线性度下降的问题。同时，本文所设计的结构，与WANG[15]提出的结构相比，在固有频率和频响平坦区相近的情况下灵敏度更高；与LI[21]提出结构相比，虽灵敏度略低，但固有频率高，且频响平坦区更宽。

表3 FBG 加速度传感器的结构性能对比Tab.3 Performance comparison of FBG accelerometer designed in this paper and reported in other Refs.

6 结 论

本文提出了一种基于轴承、柔性铰链以及对称质量块结构的中高频FBG 加速度传感器，理论分析了它的灵敏度与谐振频率，在此基础上进行了传感器结构的优化设计，制作了可扩展成为轴承铰链复合结构的双光栅加速度传感器实物。传感器封装尺寸为55×40×55 mm，体积较小，便于实际安装使用。实验研究了传感器幅频响应特性、线性响应特性、重复性及横向抗干扰特性。研究结果表明：传感器无阻尼固有频率为3 810.7 Hz，共振频率为2 200 Hz，阻尼比为0.8，稳定工作频带为10～1 200 Hz，加速度灵敏度高达17.25 pm/g，可实现中高频振动信号的测试，线性度大于0.99，重复性误差为2.33%。由于铰链刚度模型误差及封装原因，实测灵敏度与理论计算值有一定差距。后续需改进封装工艺、减小误差，同时改进轴承和铰链结构减小横向干扰。