一种基于激光雷达点云的自适应双半径滤波算法

柳斌, 李雪梅

(1.吉林化工学院 信息与控制工程学院, 吉林 吉林 132022; 2.白城师范学院 机械与控制工程学院, 吉林 白城 137000)

0 引言

近年来,智能科技的井喷式发展让智能化设备融入越来越多的产业中。自动驾驶技术能够协调出行路线与规划时间,提升驾驶安全性和交通系统运行效率。由于激光雷达优异的感知性能[1],国内外汽车产商将激光雷达广泛应用于自动驾驶汽车领域[2]。由于大气环境干扰和光电接收器件的性能差异影响,激光雷达所获取的点云数据不可避免地掺杂噪声。这些噪声直接影响点云成像的精度、特征信息提取及后续点云处理[3],因此对含噪点云进行去噪处理是点云数据预处理的关键。

目前,对点云去噪处理的方法较多。Rusu等[4]对家庭环境等真实场景下的复杂点云消除噪声,并用统计滤波在不删除重要细节的情况下对点云数据进行了重新采样。李朋超等[5]采用一种设置“基准面”和最少点数约束的体素滤波方法对点云数据进行预处理,使其满足特定位置处的处理需求。Julie等[6]设计了一种并行实现的双边滤波器,此滤波器不仅考虑了从相邻点到点的距离,而且考虑了沿法线方向的距离,以此更好地保留锋利的边缘。

Tiziana等[7]提出了一种视觉驱动点云去噪算法,该方法通过对被高斯噪声破坏的合成数据和真实数据的数值模拟来去噪。霍健等[8]提出了基于数学形态学的点云聚类算法,将去除地面后的点云分割为相互独立的点云簇,并使用自适应阈值的分布直方图去噪算法,去除点云簇周围的离群噪点。Liu等[9]提出多尺度形态与渐进式三角化不规则网络致密化相结合的分层滤波方法,具有较高的运行效率和精度。焦亚男等[10]提出基于噪声尺度变化的点云并行去噪方法,在去除不同尺度噪声的同时,模型的几何特征和点云数据的损失均较小。赵鹏等[11]将动态距离阈值与统计滤波相结合,逐渐缩小统计范围,最后采用改进双边滤波算法使数据点聚集于法向方向,从而进行光顺去噪。韩东升等[12]提出以激光点云为基准并考虑多尺度噪声滤波方法,密集匹配点云中的变形点得到了有效去除,有效提高了点云数据质量。

综上所述,现有的点云去噪算法中,传统算法仅对某一尺度的噪声去除有效[13-14],对于多尺度噪声去除需要结合多种去噪算法,势必导致运行时间相对较长,且大多算法需要人为设定滤波参数。相比之下,半径滤波运行速度快。因此本文提出一种基于自适应双半径的多尺度噪声滤波算法。通过构建自适应大、小滤波半径模型,克服半径滤波无法识别小尺度噪声的缺陷,实现自适应滤除多尺度噪声,以极大地利用半径滤波的高效性。将本文算法与各算法作对比,在去噪精确率、噪声召回率、原点保留率和运行时间等性能指标上[15],本文算法的综合性能优异。

1 经典方法

1.1 体素滤波

体素滤波是指在输入的激光雷达点云模型中建立大小可调的三维体素栅格,每个体素栅格内所有的点都被替换成它们的重心点[16],从而将激光雷达采集的密集点云在不破坏几何结构的条件下进行精简处理,同时滤除漂移噪声体素。

体素滤波的计算步骤如下:1)根据点云数据坐标集合建立三维坐标系OXYZ,分别计算X轴、Y轴、Z轴上的最大值和最小值;2)设置栅格大小Vg;3)计算能够囊括点云的最小包围盒的三维边长nx、ny、nz;4)计算体素网格的边长;5)计算每个体素栅格内点云的索引h;6)把h中的元素升序排列后计算重心点;7)用重心点代替体素栅格内的所有点。

1.2 半径滤波

半径滤波的滤波思想是在设定的半径区域内,目标点的近邻点不少于设定的阈值,若小于则认为是孤立的离群噪声,将其滤除[17]。以某点为圆心,假设滤波半径为R,在R区域内包含的点数阈值为NT。

如图1所示,若NT=1,则A、B、C三点在各自的半径R内包含的近邻点均不少于1个,三点均保留;若NT=2,则只有A点在半径R内的近邻点少于2个,因此将A点滤除,B、C两点保留;重复上述过程,直至所有点处理完毕。从滤波结果看,经过半径滤波后保留的部分是相对密集的,由此可见半径滤波对孤立噪声点的滤除效果较好。

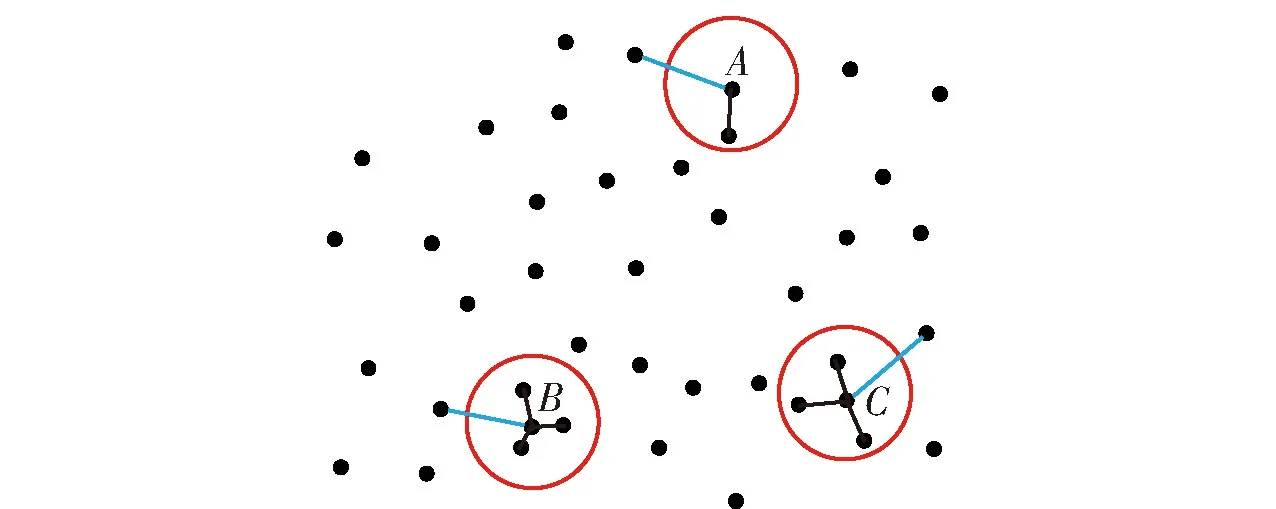
图1 半径滤波计算

1.3 统计滤波

统计滤波是指对每个点云的邻域进行统计分析,滤除分布在设定区间之外的点云。

设定每个点的近邻点数为Nsf,且点云之间的距离呈高斯分布,其分布状况由均值μ和标准差σ确定。设n和m分别为点云P中任意一点和该点邻域内任意一点的索引,计算点Pn到Pm的欧式距离S[12]:

(1)

式中:(Xn,Yn,Zn)、(Xm,Ym,Zm)分别为点Pn和Pm的三维坐标。则每个点与其邻域内所有点的欧氏距离平均值μs为

(2)

式中:n为邻域内包含的点云个数。

标准差为

(3)

为控制滤波范围,设参数k为标准差倍数,在任意点的邻域内,若近邻点与该点的欧式距离在(μs-k·σ,μs+k·σ)内则予以保留,否则剔除,k为标准差倍数。使用统计滤波方法需人工设置Nsf和k,这两个参数值选择过大会增加算法计算量和运行时间,选择过小则不能较好地体现点与近邻点之间的位置关系,导致去噪效果不佳,故选取合适的Nsf和k参数值是滤波的关键。

1.4 中值滤波

中值滤波的去噪思想非常直接,即目标点的三维坐标由邻域内所有点的三维坐标的中值代替[18]。

确定目标点P0(x0,y0,z0)的邻域,该邻域由目标点的Nmf个近邻点组成,邻域U:

U={(x0,y0,z0)|(x-x0)2+(y-y0)2+
(z-z0)2≤d2}

(4)

式中:d为P0与第Nmf个点的距离值。

对邻域内点的三维坐标分别进行升序排列:

(5)

式中:X0、Y0、Z0分别为P0邻域内点云三维坐标的集合。

用X0、Y0、Z0的中值xm、ym、zm分别替换P0的三维坐标:

(xm,ym,zm)→(x1,y1,z1)

(6)

式中:x1、y1、z1为滤波后的Po三维坐标。

从滤波思想上看,中值滤波只进行点的替换而不删除点,且能让边缘突出的噪声移到点云较密集处,因此该方法能在不损失点云数据处理精度的情况下对离群噪声点有较好的抑制作用。若中值和噪声点之间的差距较小,则中值替换的作用不明显,因此中值滤波对离群噪声簇和紧密漂移噪声滤除效果不佳。

2 自适应双半径滤波算法

2.1 设计思想及方案

应用场景和噪声类型的宽泛性要求滤波算法的泛用性良好。滤波对象数量少且形状单一,为简单场景,如某一动物、一个车体或地面路灯等;对象数量多且形状大小不一的为复杂场景,如田间作物和杂草、车载激光雷达扫描的道路和水下物体等。传统的滤波方法大多只对某一类噪声有较好的滤除效果,或只能达到某单一性能的要求。

半径滤波作为一种离群点消除方法,远比其他滤波算法迅捷高效。但半径滤波往往因不能准确识别小尺度噪声,适用性严重受限;且需要人为设定半径范围R和近邻点数NT,确定合适的参数需要大量重复测试,大大增加了处理数据的工作量。因此,若解决了适用性窄和参数设定难的问题,就能极大地利用半径滤波的高效性。

为弥补半径滤波算法的不足,本文提出构建大、小半径滤波,使之能够识别小尺度噪声;通过融合点云的密度特征,将参数设定优化为自适应调整;基于改进的体素滤波,提高运行速率。方案具体内容如图2所示。

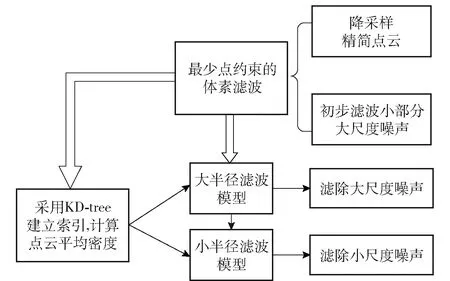
图2 去噪方案流程

本文滤波算法的滤除对象是多类型噪声,包括离群孤立噪声点和离群噪声簇等大尺度噪声,也包括紧密漂移噪声等小尺度噪声。大尺度噪声的主要特点为偏移主体点云较远,易于成簇;小尺度噪声则是与关键点糅杂在一起,不易分辨。点云经改进的体素滤波精简处理后,通过计算点云密度,构建自适应大、小半径滤波模型,以分别去除大、小尺度噪声。

2.2 程序流程图

算法设计程序包括三大部分,分别为加噪、本文算法和对比实验。具体程序流程图如图3所示。

图3 自适应双半径滤波程序流程

由图3可知,算法的代码程序分为7个步骤,具体如下:1)读取原始点云数据;2)加入均值和数量不同的高斯噪声;3)用最少点数约束的体素滤波方法来精简点云;4)计算点云平均密度;5)构建自适应大、小半径滤波模型;6)算法的性能评价;7)原始点云、加噪点云和滤波后点云的可视化。

2.3 最少点约束

体素滤波可以有效地精简点云数量,同时保留点云的形状特征,从而提高算法的运行速度,防止海量的点云数据影响后续工作。最少点约束的体素滤波在体素滤波之上添加了最少点数的限定条件,即每个体素栅格内的点数必须达到最小限定值MP,否则就扩大体素栅格范围,直至点数不少于MP。与传统体素滤波相比,在点云稀疏处的栅格内有更多的点云,因此降采样精度更高,同时滤除部分边缘离群噪声。

2.4 构建大半径滤波模型

通过融合点云密度特征,将半径滤波优化为参数自适应调整。点云的密度定义为点云中任意点与其他点之间欧氏距离的最小值,再取所有点距离最小值的平均值[19]。设点云Q中有NQ个点,其欧氏距离的最小值L为

L=min(d(p,q)),q=1,2,…,NQ-1,q≠p

(7)

式中:d(p,q)为点云Q内一点p和任意点q的欧式距离。

在不同的点云数据中,点云密度是不同的。引入可调的密度倍数参数,根据密度倍数自适应地选取合适的滤波半径。为此,构建的大半径滤波模型为

(8)

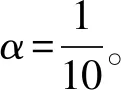
由于不同点云数据其点云密度也不同,在以点云密度为半径的圆内,每个点应有α·ML个近邻点,若没有,则说明该点的密度小于平均值,应判断为孤立噪声点。因此近邻点NL取值原则应为

(9)

式中:N+表示正整数集。

2.5 构建小半径滤波模型

经过最少点数约束和自适应大半径滤波后,离群孤立噪声点和离群噪声簇会被大幅度剔除掉,之后再加入自适应小半径滤波来去除小尺度噪声。经过降采样处理后,点云数量被精简,将原点云数据中不易分辨的漂移噪声点暴露成为“新”的离群孤立点,此时采用小半径滤波即可滤除。因此,构建的小半径滤波模型为

(10)

式中:F(RS,NS)为小滤波半径和近邻点的一组数值对,RS为滤波小半径,NS为近邻点数;β为小滤波系数;MS为密度倍数。

近邻点NS与大半径滤波模型原理相同,取值原则应为

(11)

至此,双半径滤波模型构建及参数选取完成,算法可根据不同点云数据的疏密程度自适应调整大、小滤波半径进行去噪。

3 仿真实验与分析

3.1 仿真分析

各算法的仿真实验采用的处理器均为Intel(R)Core(TM)i5-7300HQ CPU@2.50GHz、RAM为8 G、操作系统为Windos10的计算机测试,程序运行环境为Visual Studio 2022+PCL(Point Cloud Library)点云库1.12.0[20]。

实验采用斯坦福数据库中的Bunny模型进行仿真分析,如图4所示。图4(a)为Bunny模型的可视化图,点云数量为35 947;图4(b)为在原始点云上加入高斯噪声(均值为0.002 m、数量占比为25%)的可视化图,此噪声大部分为紧密的漂移噪声。

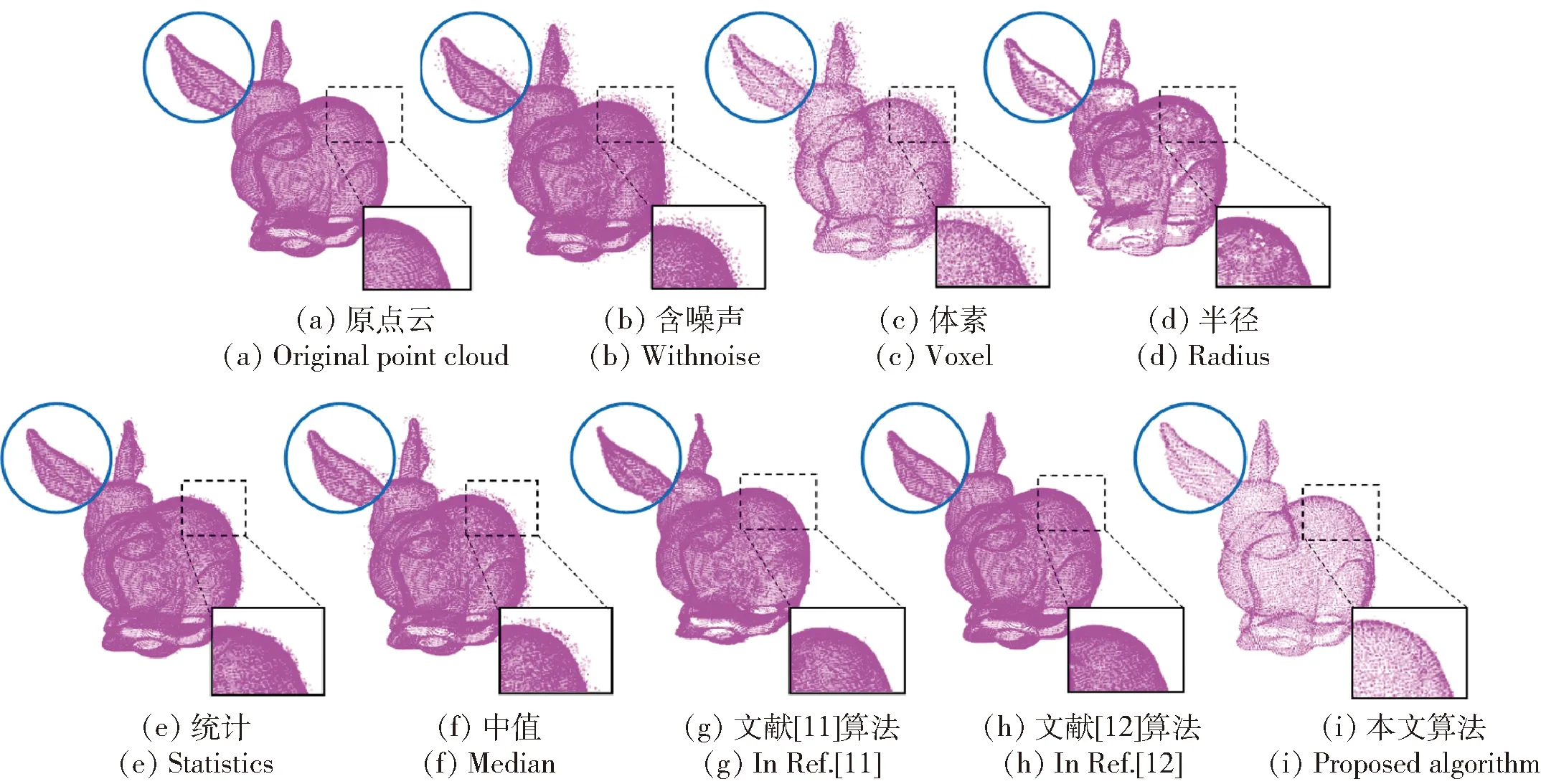
图4 Bunny模型下各滤波算法可视化图

如图4所示,体素滤波让模型的几何特征损失较小,但仍有较多离群噪声和漂移体素;半径滤波剔除了大部分噪声,但识别并不准确,破坏了一些部位的形状,导致精度损失不小;统计和中值滤波效果相近,均未能识别相当部分的噪声,中值滤波的模型背部毛刺明显较多;文献[11]算法、文献[12]算法与本文算法去噪效果相近,几何特征几乎无损失,表面光滑均无明显毛刺,绝大部分噪声被滤除,但文献[11]算法仍存在零星散落点,且模型耳朵和腿处的形状略有变化。

Bunny模型中的噪声类型较为单一,在此环境不能充分地体现各算法的优劣势。KITTI数据集是目前国际上最大的自动驾驶场景下的计算机视觉算法评测数据集[21],为进一步验证算法在复杂场景下的去噪效果,选取KITTI数据集内一段T型路口的真实场景数据,如图5所示,其中图5(a)为Road场景的可视化图,点云数量为110 090;图5(b)为加入高斯噪声(均值为0.16 m、数量占比为25%)的可视化图,图5(b)中的噪声数量较多,且类型复杂。

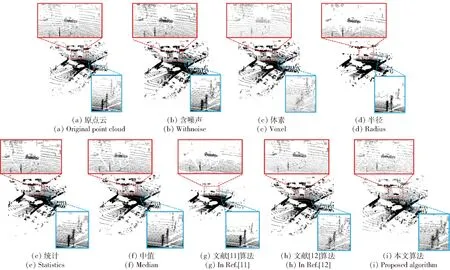
图5 Road场景下各滤波算法可视化图

图5(b)中的马路、车体及人行道红绿灯等均是重要信息,理应保留;噪声和远处的树等为无效信息,应予滤除。体素滤波后点云大幅减少,车体和噪声界线已较为模糊,大量紧密漂移体素未被滤除;半径滤波对非中心区域的云去除较多,车体周边信息所剩无几,人行道红绿灯含有杂糅的漂移噪声;统计和中值滤波效果接近,重要信息均保留完好,而统计滤波比中值滤波有更多的漂移噪声,边缘点簇也更少;文献[11]算法总体与半径滤波类似,且更进一步降低了漂移噪声数量;文献[12]算法与本文算法相近,点云密集程度均有所降低,车体和人行道红绿灯轮廓完整,进一步看细节,本文算法车体旁的漂移噪声更少,但文献[12]算法保留了更多微观上的细节。体素滤波、半径滤波、统计滤波、中值滤波和自适应双半径滤波算法的参数设置如表1所示。

表1 各滤波算法参数设置

3.2 评价指标

3.2.1 指标计算

图4和图5仅能给出算法的定性评估,下面引入去噪精确率、噪声召回率、原点保留率和运行时间,来定量对比各滤波算法的优劣。

评价指标去噪精确率Pd、噪声召回率Rd和原点保留率Ro的计算公式如下:

(12)

式中:Nq为移除的噪声数量;Ng为噪声总数;Ny为移除的点数;No为滤后剩余点云中不属于噪声的点数;Nf为滤后剩余点数。

由式(12)可知,去噪精确率和噪声召回率是衡量去噪效果的重要指标,数值越大则去噪越精准;原点保留率体现了算法对关键信息和点云精度的影响,数值越大表明精度损失越小。这些评价指标可以直观地反映算法在去噪方面的优劣程度。高斯噪声的分布由两个参数决定:均值μgn和噪声数量Ngn。μgn越大则噪声分布越分散,反之越密集。测试时,Bunny模型添加的高斯噪声均值分别为0.000 5 m、0.001 m、0.002 m、0.004 m和0.008 m,而在Road场景添加的噪声均值分别为0.06 m、0.08 m、0.12 m、0.16 m和0.18 m。此外,每个模型在固定各均值条件下,分别添加了5%、12%、17%和25%的噪声点。

3.2.2 去噪精确率

滤波算法的去噪精确率对比如图6所示。

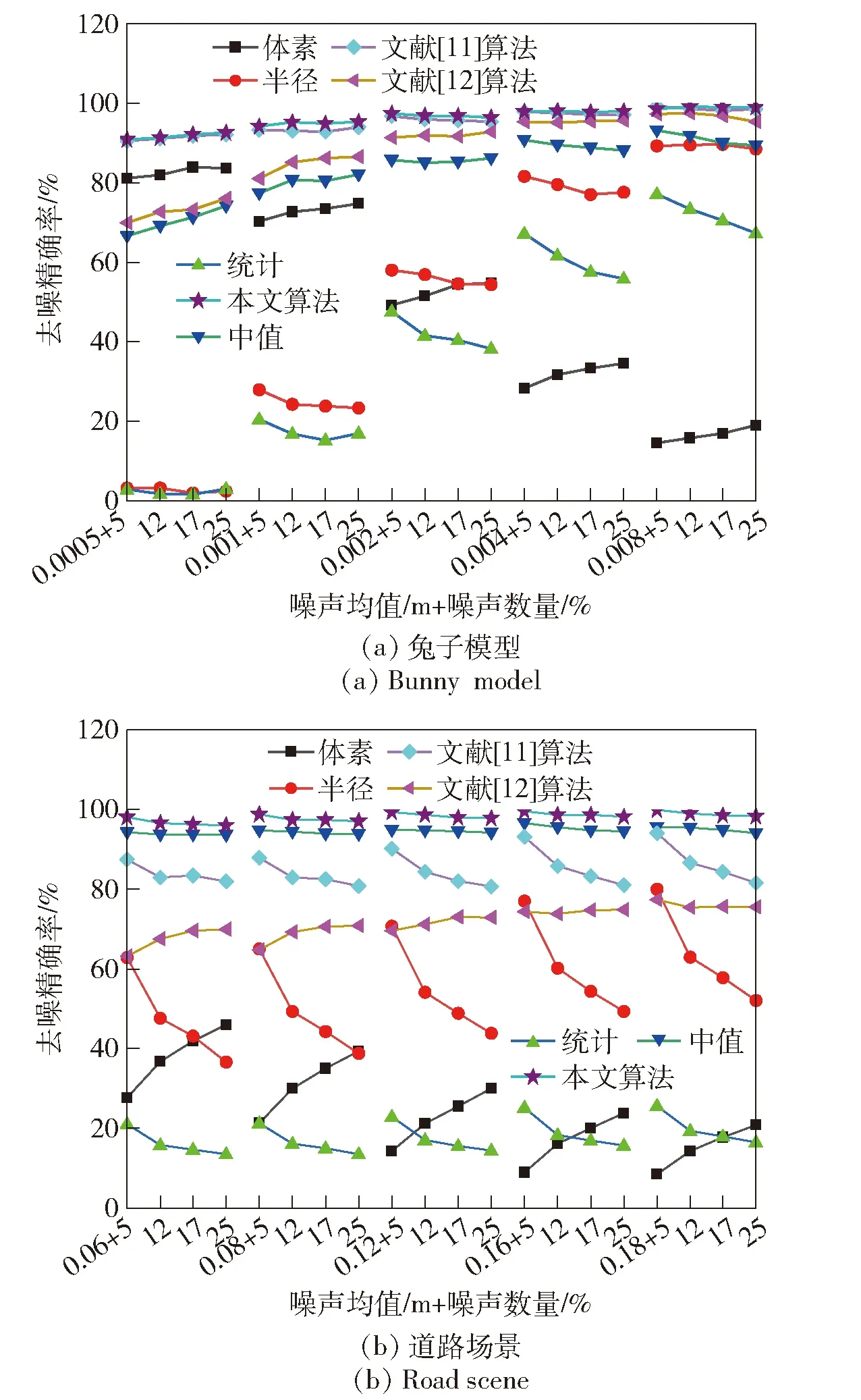
图6 去噪精确率对比(横轴刻度已省略重复的噪声均值)

在Bunny模型中,当噪声数量固定时,除中值滤波外其他算法的Pd均与噪声均值正相关;当噪声均值相同时,半径滤波、统计滤波、文献[11]算法和本文算法的Pd与噪声数量负相关,体素滤波与文献[12]算法小幅增大,中值滤波仅在低均值时小幅上升,高均值时反之。在Road场景中,Pd变化与上述情况类似,但变化方式和程度略有不同。噪声数量会对所有算法产生更大的影响,且能清晰地区分不同算法的Pd值差异,主要原因为Road场景中目标对象和噪声类型更复杂,当噪声数量足够多时易与主体混合。本文算法的Pd值在两个模型的不同噪声参数下均达到了最高水平,表明它能够有效地移除噪声,同时波动较小,因此在复杂环境中具有更强的稳定性。

3.2.3 噪声召回率

滤波算法的噪声召回率对比如图7所示。两个测试对象中,除体素滤波外各滤波算法的Rd值均与噪声均值或数量呈正相关的关系,而体素滤波与均值负相关。两者之间也有些许区别,Bunny模型的低均值下,中值滤波和文献[12]算法的Rd值明显高于文献[11]算法和本文算法,又明显高于体素滤波、半径滤波和统计滤波算法;随着均值的增大,各算法的Rd值产生分化,至中均值时已能明显区分;当高均值时统计滤波算法远高于其他算法。Road场景下各Rd值大小区分较为明显,且变化趋势高度相似。本文算法在Bunny模型中的表现在各算法对比排名中处于中下,与文献[11]算法极为相似;在Road场景中仅高于体素滤波算法。

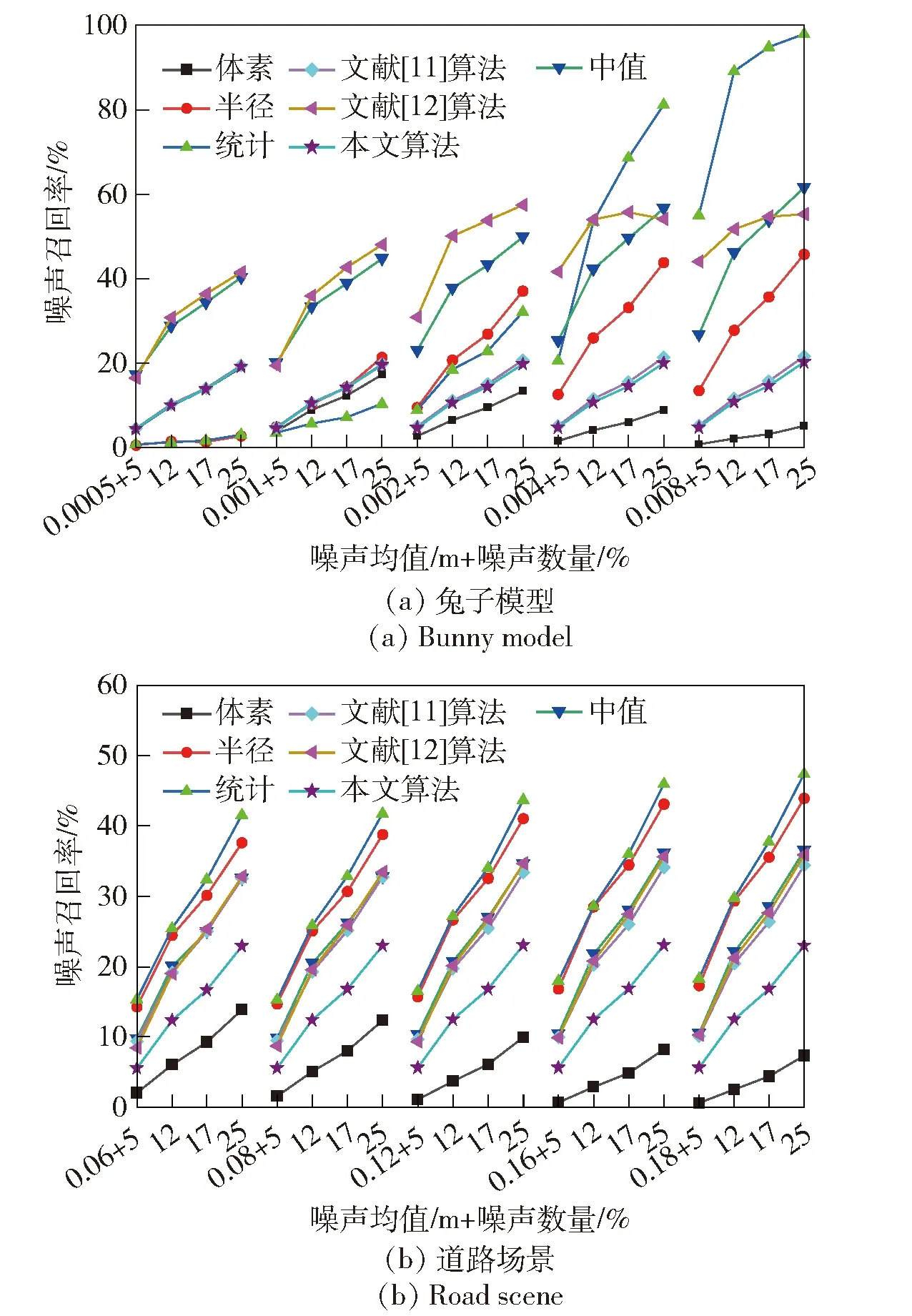
图7 噪声召回率对比(横轴刻度已省略重复的噪声均值)

图5(i)中周围车辆、会车车辆及路口信息灯均保留完整,远处噪声和其他干扰信息大量去除,由于将远处非紧要点云删除,且采用最少点数约束的体素滤波进行降采样精简点云,导致式(12)中Ny过大,从而降低了Rd值。因此,仅对比Rd值并不能将滤波前后精度损失的程度作全面具体的对比,需要引入第3个评价指标原点保留率Ro。

3.2.4 原点保留率

滤波算法的原点保留率对比如图8所示。

原点保留率定义为滤后点云中的原始点云数量所占比例,反映了点云信息保留的程度,也用于衡量点云处理过程中对原始信息的影响程度。如图8所示,在Bunny模型和Road场景中,非体素滤波算法的Ro均与噪声数量负相关,与均值正相关,而体素滤波算法均为负相关。本文算法的原点保留率高,与文献[11]算法、文献[12]算法相近;中值滤波算法只是替换噪声而没有删除,因此其Ro值高。本文算法利用最少点约束的体素滤波扩大点间距,因此半径滤波算法对离群点敏感的优势得以充分发挥,只损失少部分原有的点。在噪声占比上升的情况下Ro下降幅度相对较小,反映出本文算法具有广泛的适用性和较强的鲁棒性。

综合以上3个反映去噪精度的评价指标,本文算法的去噪精度比各传统算法更高,与文献[11]算法和文献[12]算法相比略低,仍能证实本文构建的自适应大、小半径滤波模型弥补了半径滤波算法不适用于小尺度噪声的缺陷,大幅度拓展了算法的适用范围。

3.2.5 运行时间

面向实际应用场景,算法的运行时间是需要关注的重要性能指标,各滤波算法的运行时间对比如图9所示。

图9 运行时间对比(横轴刻度已省略重复的噪声均值)

在仿真测试中,通过运行各算法200次,并取算术平均值来获取图9中的运行时间数据,以更准确地评估各算法的表现。由图9可见,对于测试对象,所有算法的运行时间均与噪声均值和数量呈正相关关系;文献[11]算法用时明显高于文献[12]算法,且大幅高于其他算法;统计、中值、半径、体素和本文滤波算法在Bunny模型中均低于1.2 s,在Road场景下均低于5 s;本文算法用时略高于半径和体素滤波算法,而低于统计滤波和中值滤波算法;当噪声占比升高时,统计和中值滤波算法用时显著升高,因为它们都需要对邻近点计算距离,导致它们对噪声数量敏感。本文算法采用双半径滤波而仅比传统半径滤波算法用时略高一点,是因为先用最少点数约束的体素滤波精简了点云数量,并在计算点云密度时先构建了KD-tree,因此需要搜索的近邻点数量大幅缩小,从而加快了搜索进程,达到近似单半径滤波的运行速率。

4 结论

本文将最少点约束条件下的体素滤波和半径滤波相结合,并融合点云的密度特征,构建了自适应大、小半径滤波模型,提出一种基于激光雷达点云的自适应双半径滤波滤波方法。实验结果显示,去噪精确率和原点保留率均在90%以上,且运行时间低于2 s;新算法具有优秀的去噪效果和低的精度损失,同时运行速度也非常快。即使面对复杂的噪声类型和大量的噪声数量,去噪性能仍然出色,验证了新算法的有效性和强鲁棒性。本文结果为自动驾驶车辆激光雷达点云目标的检测、识别、定位与跟踪等方法的点云预处理提供了理论参考。