篦齿封严气弹稳定性影响因素研究*
2023-10-07苏国征徐梅鹏
苏国征 孙 丹 王 志 李 玉 王 文 徐梅鹏
(1.沈阳航空航天大学航空发动机学院,辽宁省航空推进系统先进测试技术重点实验室 辽宁沈阳 110136;2.沈阳航空航天大学沈阳市透平机械先进密封技术重点实验室 辽宁沈阳 110136;3.中国航发商用航空发动机有限责任公司 上海 200241)
篦齿封严是航空发动机中重要的封严部件,用于限制工作介质的泄漏[1-2]。随着航空发动机向高推重比和高轴功率方向发展,篦齿封严工作转速增大,封严压力提高,结构质量减轻,导致齿腔压力波动与结构振动相互耦合引发的气弹失稳问题愈发突出,时有发生因气弹失稳导致篦齿封严出现裂纹甚至断裂的故障问题[3-4]。因此,研究篦齿封严气弹稳定性具有重要学术价值和工程意义。
ALFORD[5-6]首次提出篦齿封严气弹失稳会引起篦齿封严组件的高周疲劳故障,指出低压侧的支撑架自由端更易发生失稳,可以通过增加密封刚度来提高密封固有频率进而提高密封稳定性。国内外研究人员通过理论研究,分析了篦齿封严气弹稳定性相关影响因素。PHIBEL等[7]通过求解非定常气动力对篦齿封严所做气动功,指出篦齿封严气弹稳定性与非定常压力分布、模态振型以及空腔形状有关。SRINIVASAN等[8]提出一种将定子和转子视为柔性元件计算气弹失稳的方法,指出气动阻尼突然变化不利于篦齿封严系统稳定。DI MARE等[9]应用综合时域法对某发动机涡轮密封进行颤振分析,并对篦齿封严结构进行了改进。ZHUANG等[10]采用非定常雷诺平均求解器研究了对篦齿封严气弹稳定性有重要影响的各种参数。李辉等人[11]采用双控制体模型计算了篦齿封严的气动刚度和气动阻尼,研究了进出口压差和进口气流预旋速度对气弹稳定性的影响。齐鹏逸等[12]研究了转子稳定性控制方法,并结合控制理论开发了实时控制系统。此外,部分学者试验研究了影响篦齿封严稳定性的结构形式和工况条件。MIURA和SAKAI[13]数值与试验研究了不同结构形式的密封间隙对气弹稳定性的影响,提出且验证了改良气弹失稳的一种结构。张万福等[14-15]试验研究了不同转速、进口压力和涡动频率对交错式迷宫密封动力特性系数及迷宫密封稳定性的影响规律。另外,部分研究人员采用数值仿真方法,研究了篦齿封严结构与工况参数对稳定性的影响规律。宁喜等人[16]采用CFD方法预测了不同形式密封的动力特性与转子稳定性。王能茂等[17-18]利用能量法,计算了气动功和模态气动阻尼比,通过二者正负值来判断篦齿封严是否发生气弹失稳。综上所述,现有文献大多研究结构与工况参数对篦齿封严气弹稳定性的影响,关于篦齿封严气弹稳定性理论研究较少,鲜有篦齿封严气弹失稳机制研究的文献报道。
本文作者应用数值模拟与气弹稳定性判定公式相结合的方法,建立了篦齿封严气弹稳定性求解模型,在验证了数值求解方法以及判定公式准确性的基础上,研究了齿间距、壁厚和转速对篦齿封严气弹稳定性的影响规律,并揭示了篦齿封严气弹失稳机制。文中研究结果为篦齿封严气弹稳定性结构设计提供理论参考。
1 篦齿封严气弹稳定性理论分析
1.1 结构动力学理论分析
多自由度无阻尼自由振动方程[19-20]为
(1)
假设篦齿封严按照简谐规律振动,则有
{x}={A}sin(ωt+α)
(2)
式中:{x}为振动位移;[M]、[K]分别为质量矩阵和刚度矩阵;{A}为篦齿封严振动振型;ω为篦齿封严固有频率;α为篦齿封严振动的初始相位角。
将式(2)代入式(1)中,化简整理并振型归一化,得到
(-ω2[M]+[K]){q}=0
(3)
根据振型第一正交性和第二正交性,对于任意两阶不同主振型,质量矩阵[M]、刚度矩阵[K]分别正交,即
(4)
(5)
式中:{q}i、{q}j为任意两阶不同主振型。
对于同一阶振型i=j时,令
(6)
(7)
对于主振型矩阵{Q},则有
{Q}T[M]{Q}=[MP]
(8)
{Q}T[K]{Q}=[KP]
(9)
1.2 气弹稳定性判定公式
篦齿齿高相对于篦齿环半径很小,可忽略不计,将篦齿环简化为光面圆环,弯曲圆环的固有频率[21]为
(10)
式中:n为节径数;E为弹性模量;I为材料横截面对弯曲中性轴的惯性矩;g为重力加速度;ρ为材料密度;A为横截面积;R为半径。
将篦齿封严的质量M=2πRρA代入式(10)整理得到
(11)
篦齿封严径向变形公式[4]为
(12)
式中:w为径向变形量;p0为压力;L为轴向长度。
将式(11)、(12)两式联立整理得
(13)
则有最大径向变形系数φ[5-6]
(14)
式中:Mω为参与振动有效质量。
对于一端固定支撑的篦齿封严,当φ小于0.4×10-3时气动弹性表现为稳定;对于两端固定支撑的篦齿封严,当φ小于2.0×10-3时表现为气弹失稳。2种支撑形式如图1所示。现将最大径向变形系数w/R取以10为底的对数即lgφ,记为δ,定义为径向对数变形率,满足以下条件即为气弹稳定状态:
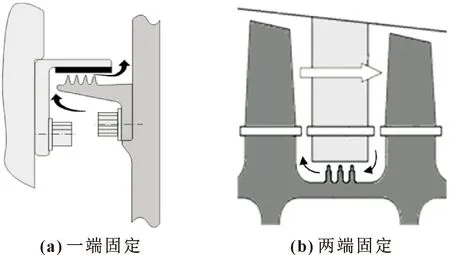
图1 支撑形式[6]Fig.1 Support form[6]:(a)fixed at one end;(b)fixed at two end
(15)
对于文中模型,固定形式为一端固定,记δr为稳定临界值,即δr=-3.398。
2 篦齿封严气弹稳定性数值模型
2.1 求解模型
文中计算模型取自航空发动机某原型机上典型篦齿封严结构,建立了篦齿封严数值求解模型。其主要结构包括转轴、转接件、内篦齿环和外篦齿环,图2给出了篦齿封严原始结构模型。
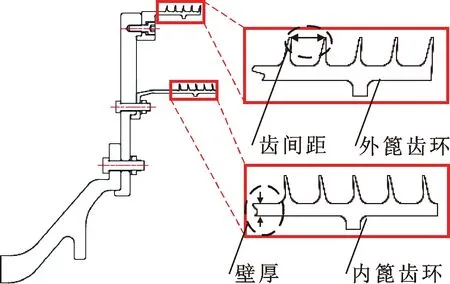
图2 篦齿封严模型尺寸Fig.2 Labyrinth seals model size
转轴材料采用1Cr11Ni2W2MoV,该材料具有马氏体相变硬化能力,具有良好的综合力学性能。转接件和内外篦齿环材料采用GH4169,该材料是一种强化镍基高温合金,具有很好的屈服强度以及抗疲劳、耐腐蚀性能。表1给出了20 ℃下各材料的力学性能[22]。

表1 材料力学性能(20 ℃)[22]Table 1 Mechanical properties of materials(20 ℃)[22]
篦齿封严气弹稳定性数值求解模型如图3所示,模型由转轴、转接件以及内外篦齿环四部分组成,内外篦齿环齿距、齿高均相等,齿数为5,倾斜角相等、倾斜方向相反。
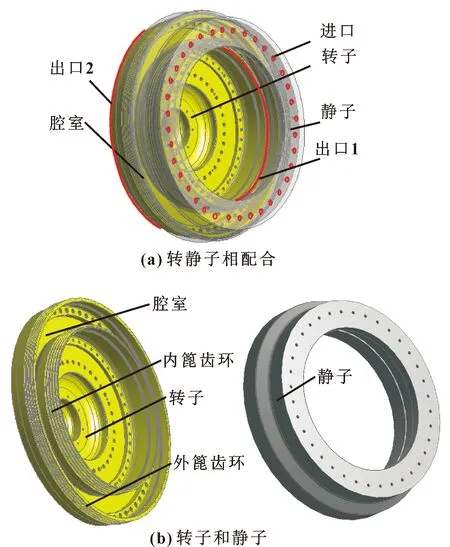
图3 篦齿封严气弹稳定性数值求解模型Fig.3 Aeroelastic stability numerical solution model of labyrinth seals:(a)rotor combined with stator;(b)rotor and stator
2.2 网格划分
图4示出了篦齿封严网格划分结果,采用网格分区划分的方式,对于内外篦齿环以及转接件采用规则六面体网格划分,对于不便于切分且对结果影响较小的转轴采用四面体网格划分。以篦齿封严第2节径(nodal diameter,ND)固有频率为特征参数,对不同的网格数量进行网格无关性验证,选取合理的网格数量,结果示于图5。综合考虑计算精度和计算效率,最终确定基础模型网格数量为280万,其中周向节点数80,密封齿腔的轴向节点数为10,密封齿腔径向节点数为15,其他计算模型网格数量为265万~300万。
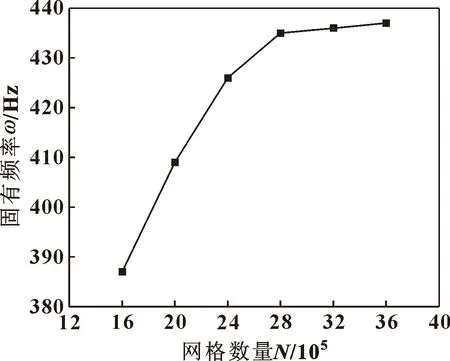
图5 第2节径固有频率与网格数量的关系曲线Fig.5 Relation curve between natural frequency of 2ND and mesh number
2.3 边界条件
文中计算了篦齿封严在不同齿间距、壁厚以及不同转速情况下的固有频率和气弹稳定性,相关参数见表2。边界条件为对轴端施加远端位移约束,约束轴向的平动和转动,设置转速0~9 000 r/min,步长为3 000 r/min,考虑离心力对模态的影响。相关约束条件如图6所示。

表2 流体参数Table 2 Fluid parameters

图6 边界条件Fig.6 Boundary conditions
2.4 准确性验证
为验证文中求解结构动力特性数值方法与气弹稳定性判定公式的准确性,建立了参考文献[13]中的数值模型,该文数值与试验研究了不同结构形式的篦齿封严齿间隙对气弹稳定性的影响。
如图7所示,对图中相应位置施加固定约束。采用文中数值方法对该模型求解动力学特性,应用稳定性判定公式预测该模型的气弹稳定性。文献[13]中的流体边界条件如表3所示。

表3 流体域边界条件[13]Table 3 Fluid boundary conditions[13]

图7 固体域边界条件[13]Fig.7 Solid boundary conditions[13]
采用文中的数值方法计算得到固有频率,与参考文献[13]中的结果进行对比,由于试验中存在机械阻尼,而文中数值计算方法忽略了机械阻尼[20]对模态频率的影响,如式(3)所示,导致仿真结果与参考文献试验值存在一定误差。如图8所示,数值仿真结果与文献[13]中试验结果平均相对误差5.8%,吻合良好。
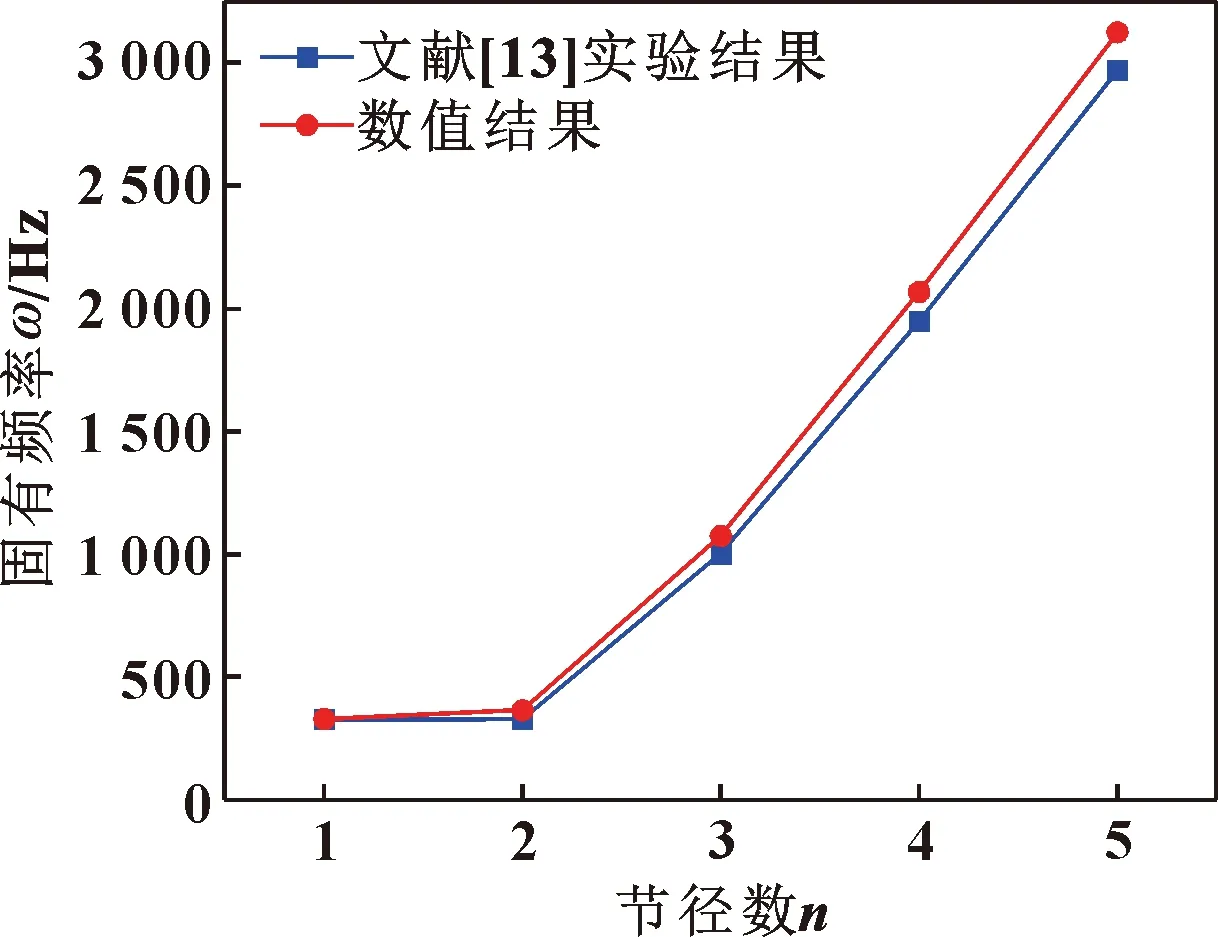
图8 固有频率准确性验证Fig.8 Accuracy verification of natural frequency
为验证气弹稳定性判定标准的适用性,文中在数值求解文献[13]中篦齿封严固有频率的基础上,通过判定公式(14),判断了篦齿封严2~5节径气弹稳定性,与文献[13]对比结果如表4所示。结果表明,从定性的角度判断篦齿封严是否发生气弹失稳,判定公式(14)与文献[13]的判定标准具有良好的一致性。

表4 气弹稳定性准确性验证Table 4 Accuracy verification of aeroelastic stability
3 计算结果及分析
3.1 篦齿封严模态分析
图9给出了同一篦齿封严模型1~8节径模态振型。从第5节径开始,篦齿封严环主振动形式开始出现明显区别,即内篦齿环振动剧烈时,外篦齿环振动微弱,或反之。如图9(e)(f)所示,同为第5节径振动,图9(e)中内篦齿环振动剧烈,但外篦齿环振动相对微弱,是以内篦齿环做主振动的模态振型,图9(f)反之,是以外篦齿环做主振动的模态振型。节径数越大,2种主振动形式的固有频率相差越大。
3.1.1 齿间距对篦齿封严模态影响分析
图10和图11给出了篦齿封严齿间距对固有频率的影响规律,可以看出,篦齿封严的固有频率均随齿间距的增加而减小。齿间距对篦齿封严前3节径的固有频率影响较小,最大降低8.02%;从第4节径开始,齿间距对固有频率的影响明显增大,尤其是对以外篦齿环做主振动的模态固有频率影响更加显著;同时也表明篦齿环半径越大,固有频率对齿间距的变化越敏感。篦齿封严齿间距的增加,对以内篦齿环做主振动时的第5节径固有频率影响最大,该阶固有频率降低14.63%;对以外篦齿环做主振动时的第7节径固有频率影响最大,最大降低23.51%。齿间距的增加会引起封严长度的增加,进而引起质量的增加,继而导致固有频率的降低。
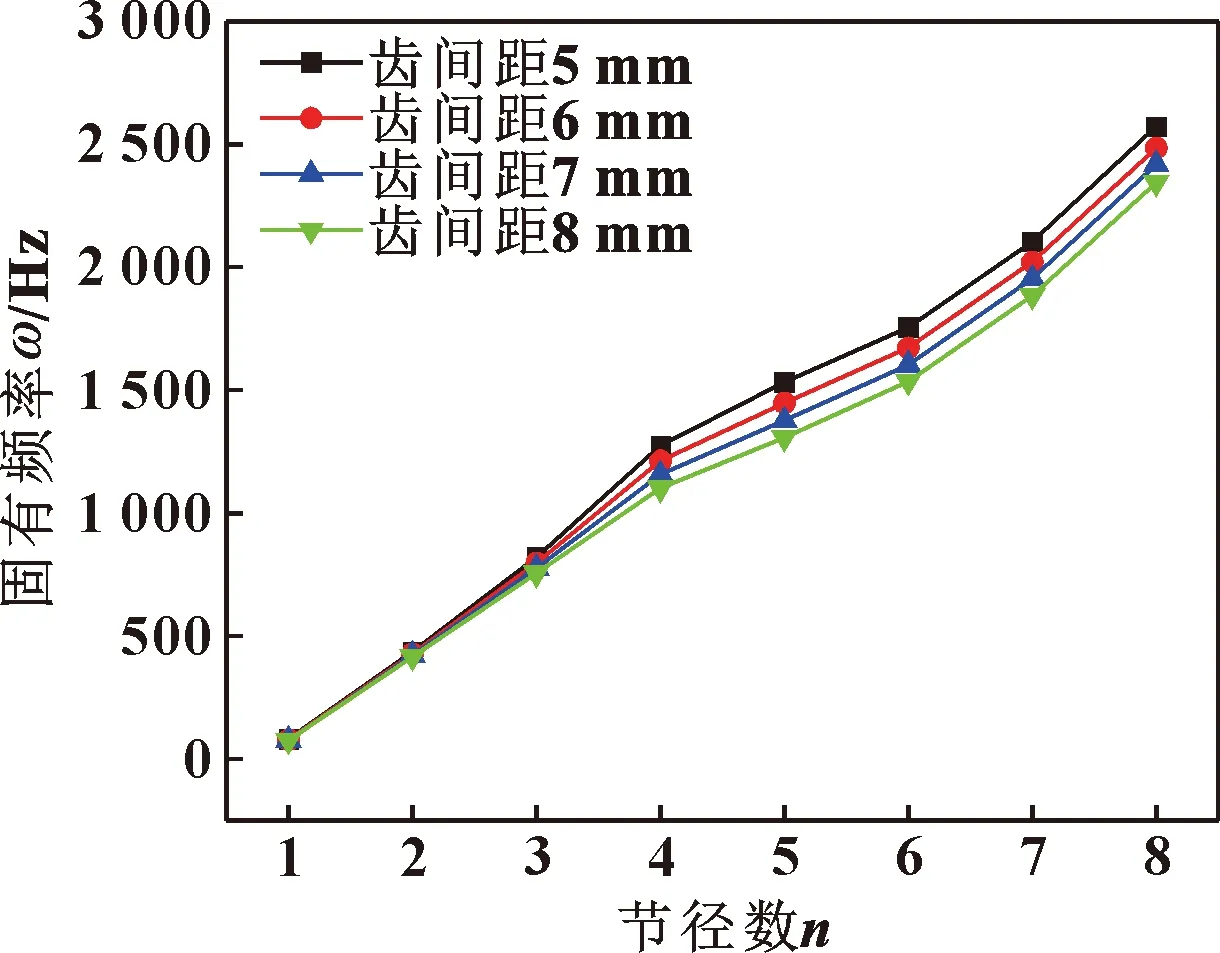
图10 内篦齿环做主振动的固有频率随齿间距变化规律Fig.10 The natural frequency of interior labyrinth seal ring vibration versus cavity width
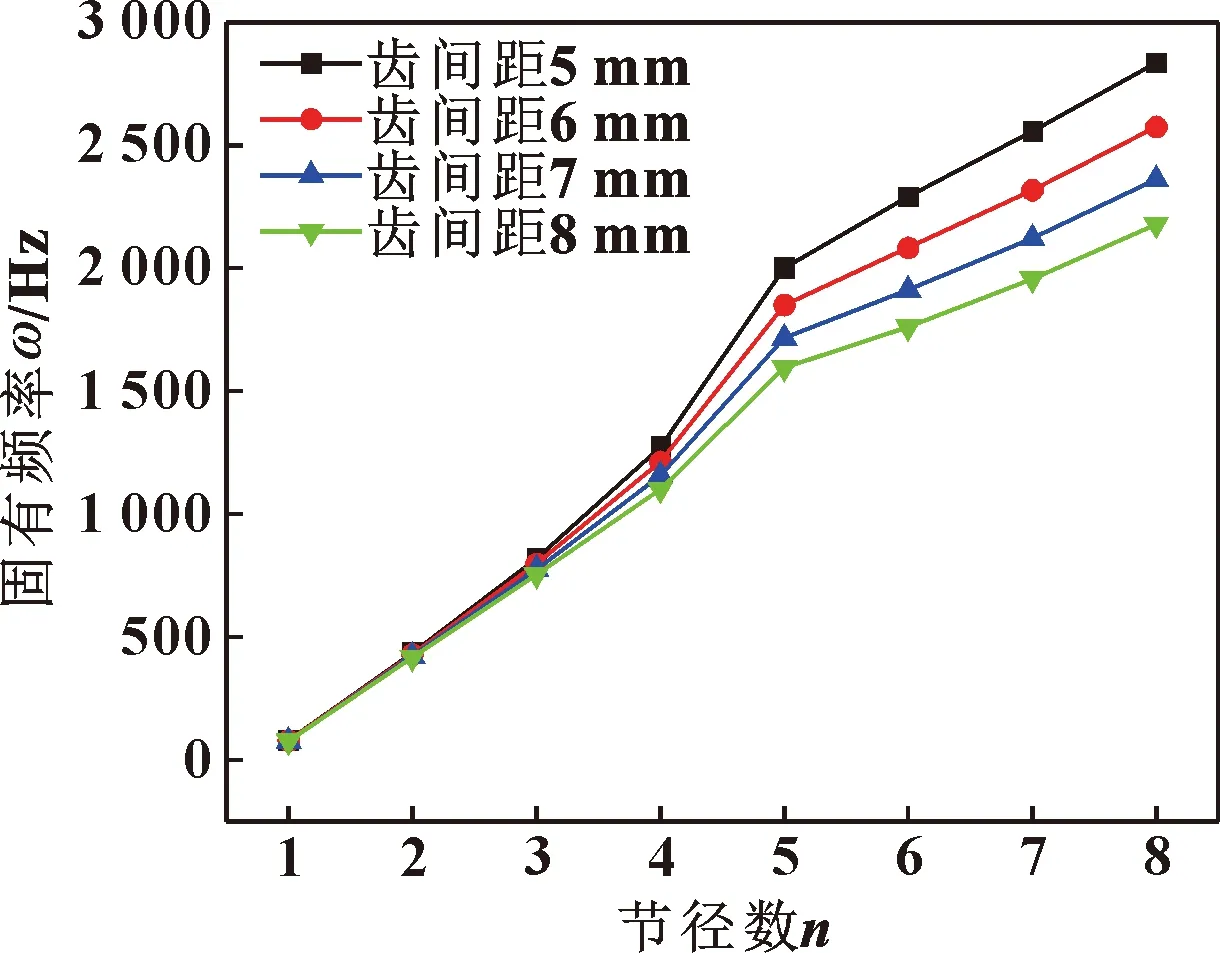
图11 外篦齿环做主振动的固有频率随齿间距变化规律Fig.11 The natural frequency of exterior labyrinth seal ring vibration versus cavity width
3.1.2 壁厚对篦齿封严模态影响分析
图12和图13给出了篦齿封严齿壁厚对固有频率的影响规律。可以看出,随着篦齿封严壁厚的增加,篦齿封严的固有频率在增大,并且是在第4节径开始显著变化;节径数越大,篦齿封严壁厚对固有频率影响越大,并且以外篦齿环做主振动的固有频率对壁厚变化的敏感程度要高于以内篦齿环做主振动的形式。随着篦齿封严壁厚的增加,以内篦齿环做主振动的固有频率最大增加15.20%,发生在第7节径;以外篦齿环做主振动的固有频率最大增加19.28%,发生在第8节径。篦齿封严为薄壁零件,壁厚的增加会引起篦齿封严结构刚度的明显增加;壁厚增加的同时也会引起篦齿封严质量的增加,篦齿封严壁厚增加对篦齿环固有频率的影响,需要综合考虑结构刚度的改变和质量增加的影响,根据固有频率与结构刚度和质量的关系,篦齿封严壁厚的增加引起固有频率的增加,说明结构刚度增加对固有频率的影响要远大于质量增加的影响。
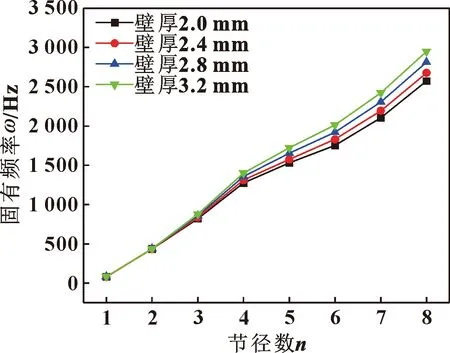
图12 内篦齿环做主振动的固有频率随壁厚变化规律Fig.12 The natural frequency of interior labyrinth seal ring vibration versus wall thickness differential
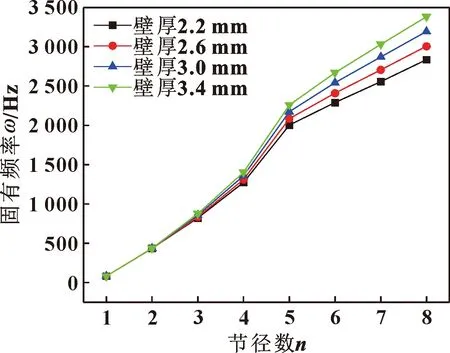
图13 外篦齿环做主振动的固有频率随壁厚变化规律Fig.13 The natural frequency of exterior labyrinth seal ring vibration versus wall thickness differential
3.1.3 转速对篦齿封严模态影响分析
图14和图15给出了转速对固有频率的影响规律。可以看出,随着转速的增加,篦齿封严固有频率在增加,在低转速时,固有频率变化不明显,而且转速越高,对篦齿封严固有频率的影响越大。篦齿封严工作转速的增加对于第1阶固有频率影响最大,工作转速9 000 r/min相比于转速为0,篦齿封严固有频率最大增加95.05%。由于转速的增加,离心力在逐渐增大,进而引起篦齿环径向正应力的增加,使篦齿环刚度增加,从而导致固有频率的增加。由于半径越大离心力越大,故而在相同条件、相同节径下,以外篦齿环做主振动的固有频率要高于以内篦齿环做主振动的固有频率。
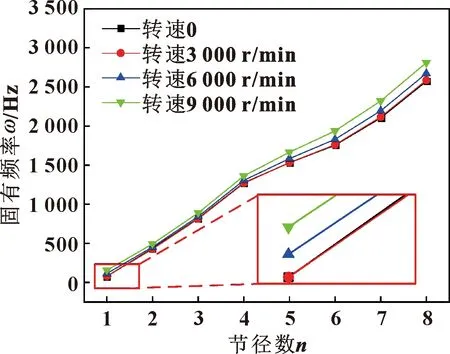
图14 内篦齿环做主振动的固有频率随转速变化规律Fig.14 The natural frequency of interior labyrinth seal ring vibration versus rotating speed differential
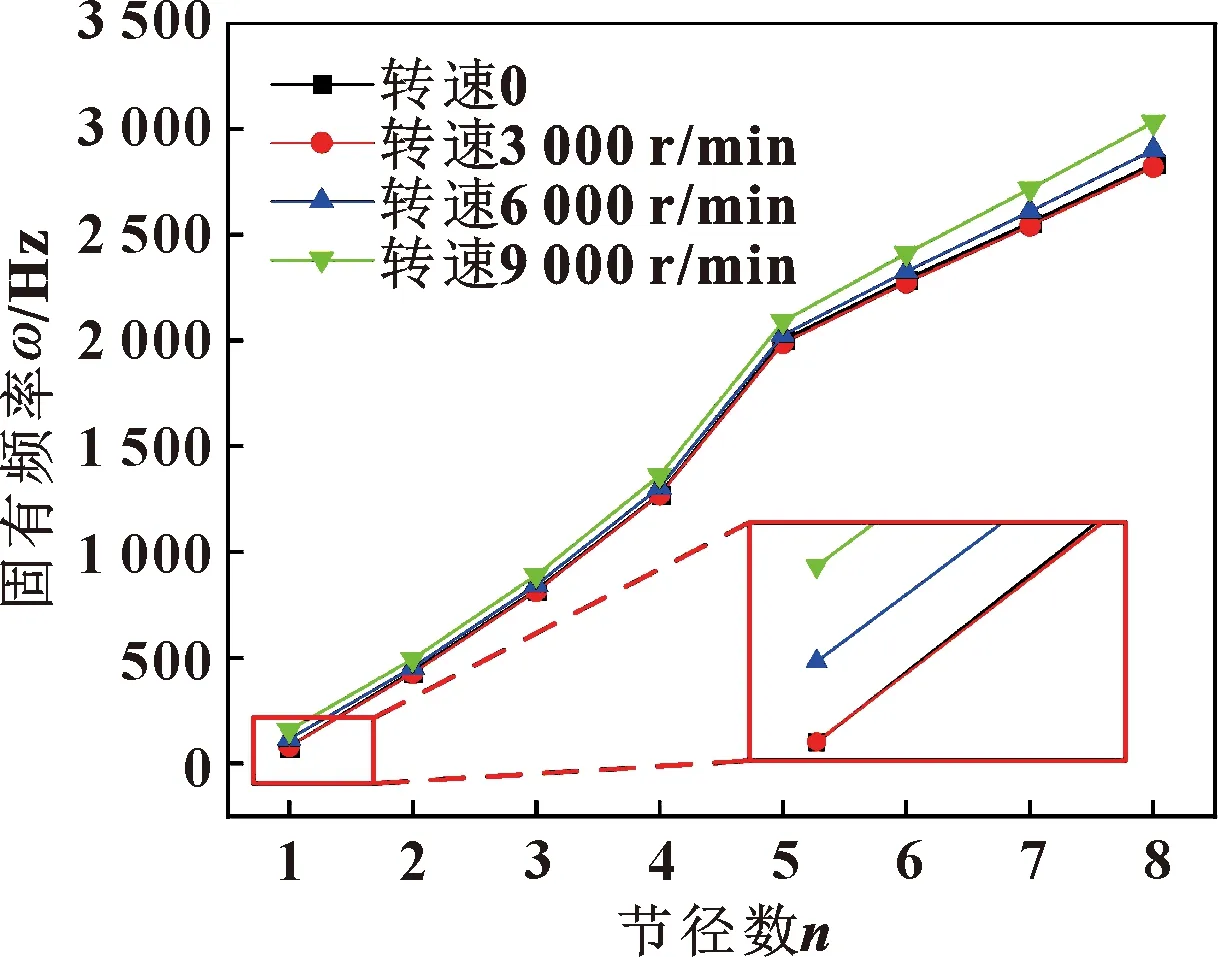
图15 外篦齿环做主振动的固有频率随转速变化规律Fig.15 The natural frequency of exterior labyrinth seal ring vibration versus rotating speed differential
3.2 篦齿封严气弹稳定性分析
3.2.1 齿间距对篦齿封严气弹稳定性影响
图16和图17给出了内、外篦齿环气弹稳定性随齿间距变化规律,在节径数大于等于2时,随着齿间距的增加,径向对数变形率在增大,对内篦齿环第4节径和外篦齿环第6节径径向对数变形率影响最大。篦齿封严齿间距增加3 mm,可导致内篦齿径向对数变形率最大升高7.56%,外篦齿径向对数变形率最大升高8.54%;同时内篦齿环的第5节径和第6节径由稳定状态转变为失稳状态。随着齿间距的增加,外篦齿环并没有某个节径振动由稳定状态转变为失稳,说明外篦齿环的气弹稳定性对于齿间距变化的敏感程度要弱于内篦齿环。由3.1.1节分析可知,随齿间距的增加,篦齿环各节径固有频率降低,篦齿环封严长度增加,质量增加,根据气弹稳定性判定公式可知,随着篦齿环齿间距的增加,封严长度和频率共同作用的影响超过模态质量增加的影响。而固有频率是由质量和刚度决定,根据气弹稳定性判定公式和固有频率与刚度、质量的关系,封严长度增加的影响对于气弹稳定性的降低起主要作用。
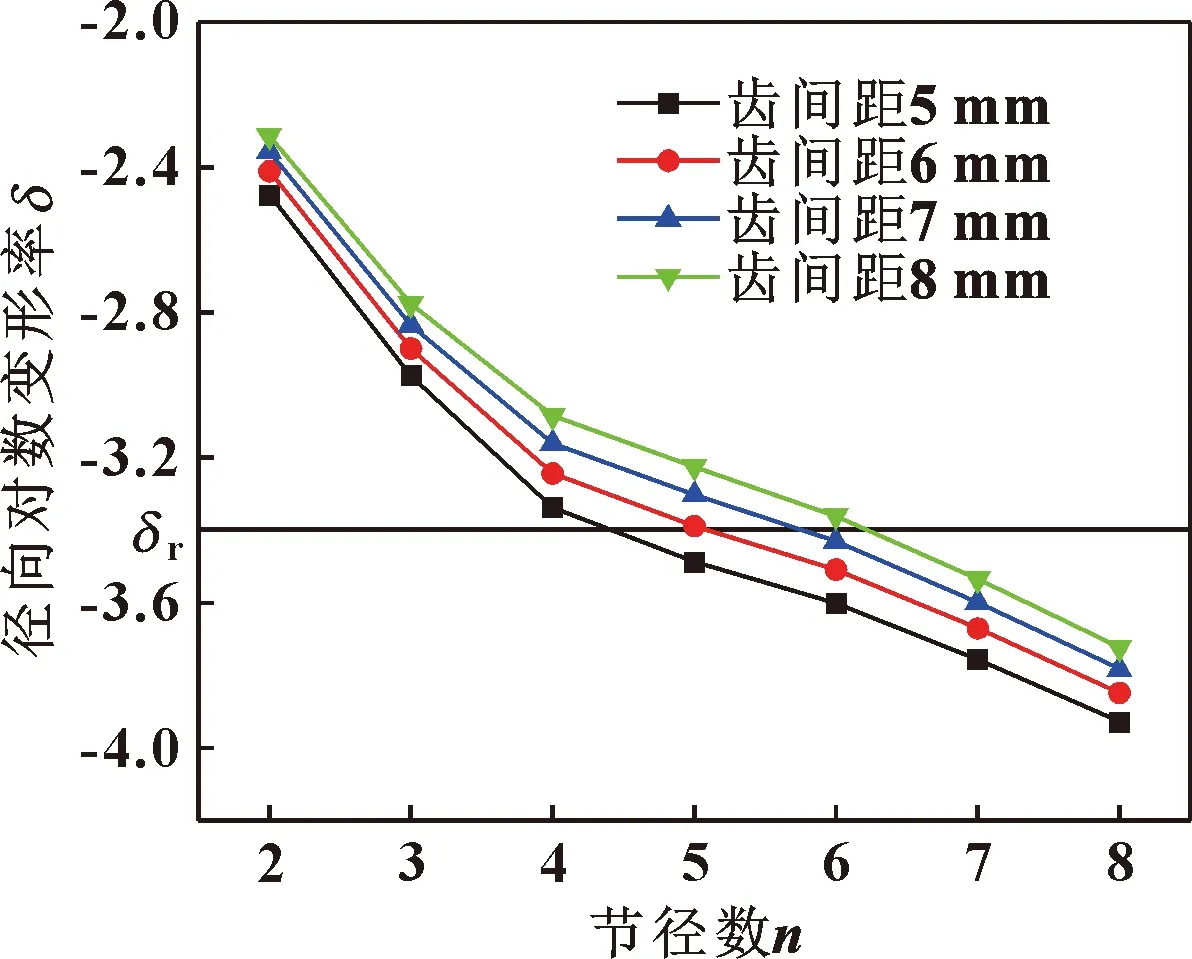
图16 内篦齿环气弹稳定性随齿间距变化规律Fig.16 The aeroelastic stability of interior labyrinth seal ring versus cavity width differential
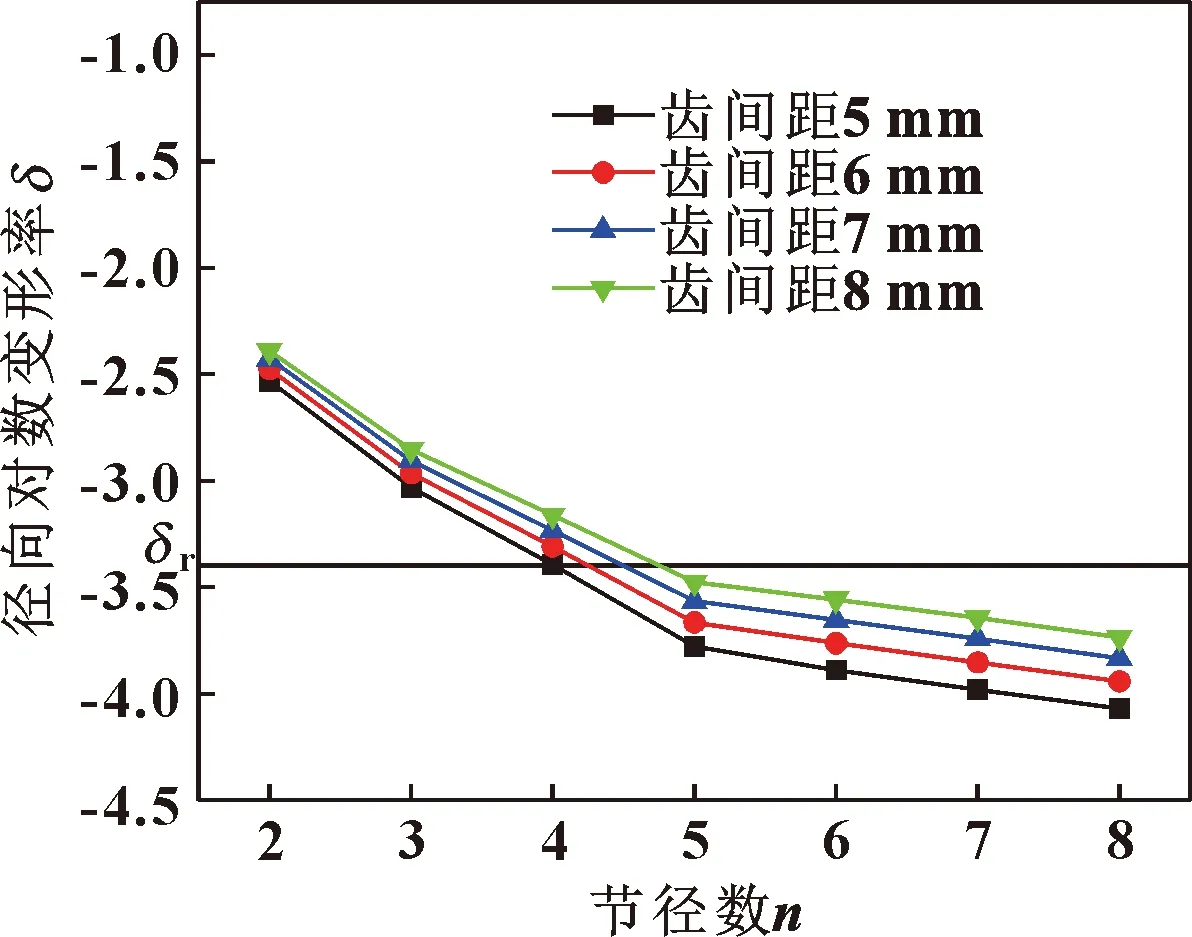
图17 外篦齿环气弹稳定性随齿间距变化规律Fig.17 The aeroelastic stability of exterior labyrinth seal ring versus cavity width differential
3.2.2 壁厚对篦齿封严气弹稳定性影响分析
图18和图19给出了篦齿封严齿壁厚对篦齿封严气弹稳定性的影响规律。可以看出,对于大于等于2的节径,随着篦齿环壁厚的增加,径向对数变形率在减小,内、外篦齿环的气弹稳定性在增加。篦齿封严壁厚增加1.2 mm,可引起内篦齿径向对数变形率最大降低6.70%,外篦齿径向对数变形率最大降低7.00%,第4节径由临界稳定转变成了稳定状态,同时使第3节径径向对数变形率更加接近临界值。由于壁厚的增加,篦齿环模态质量在增加,且由于结构刚度增加导致固有频率在升高,在2个量共同作用下导致径向对数变形率的降低,故而篦齿环的气弹稳定性得到有效改善。
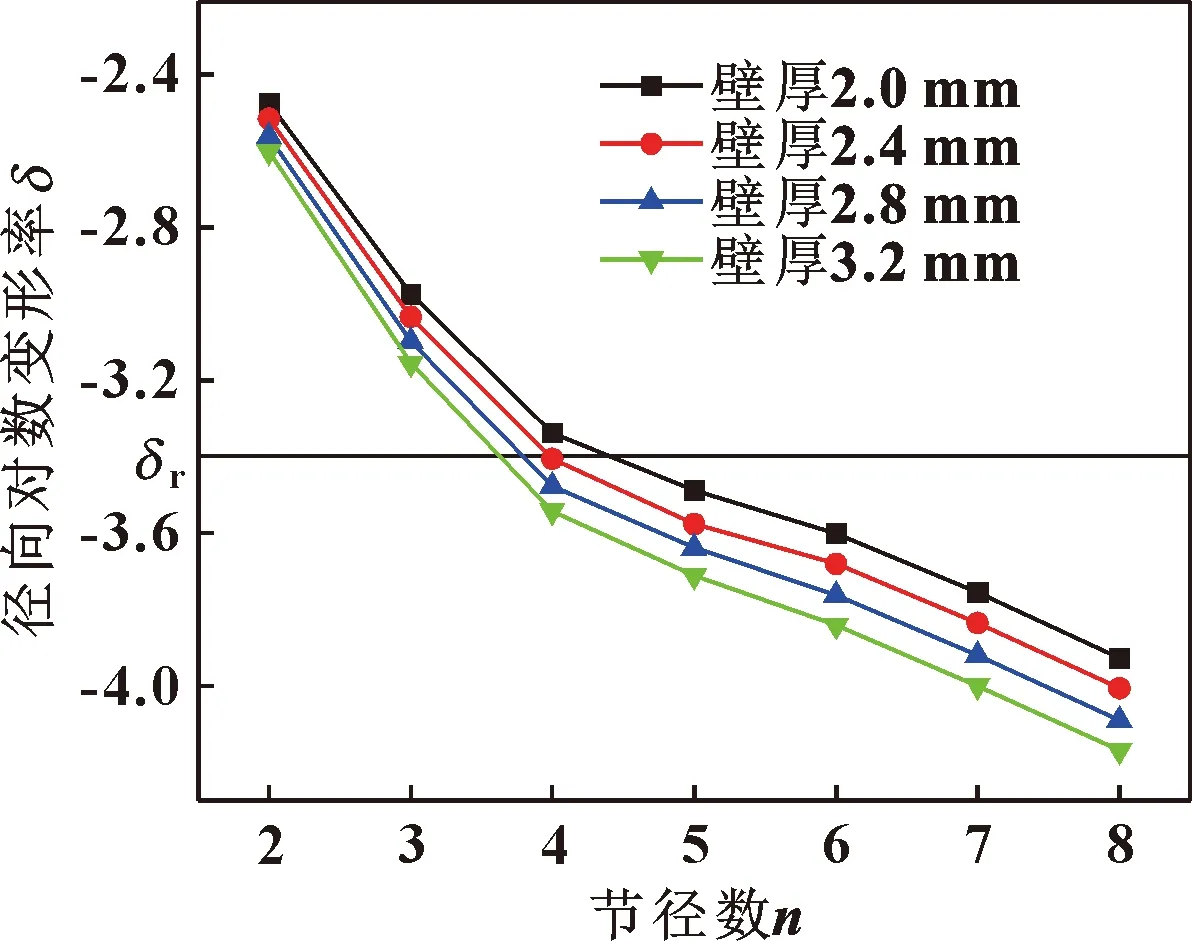
图18 内篦齿环气弹稳定性随壁厚变化规律Fig.18 The aeroelastic stability of interior labyrinth seal ring versus wall thickness differential
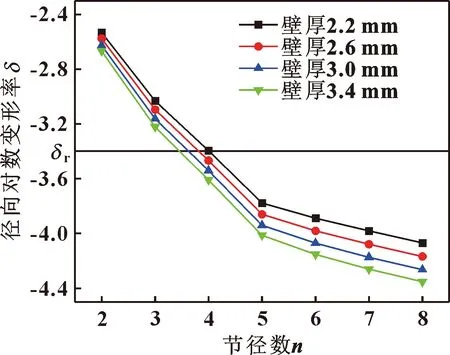
图19 外篦齿环气弹稳定性随壁厚变化规律Fig.19 The aeroelastic stability of exterior labyrinth seal ring versus wall thickness differential
3.2.3 转速对篦齿封严气弹稳定性影响分析
图20和图21给出了篦齿封严随转速的变化规律,当节径数大于等于2时,随着转速的增加,各节径下的径向对数变形率在减小,有稳定性增加的趋势,但转速增加对于篦齿环气弹稳定性的影响甚微。转速对第2节径径向对数变形率影响稍大,其中内篦齿环降低4.35%,外篦齿环降低4.25%,但并没有改变气弹失稳状态。外篦齿环转速由0升到9 000 r/min,第4节径由临界稳定转变成了稳定,低于9 000 r/min时,转速对篦齿封严气弹稳定性影响较小,证明只有在高转速下,篦齿环转速才会对气弹稳定性产生相对较明显影响。转速会使篦齿封严产生离心力,离心力会使篦齿封严的固有频率增加,从而使径向对数变形率减小。但较小的转速,产生离心力较小,对篦齿封严固有频率影响较小,进而对径向对数变形率产生较小的影响,对气弹稳定性影响很小。
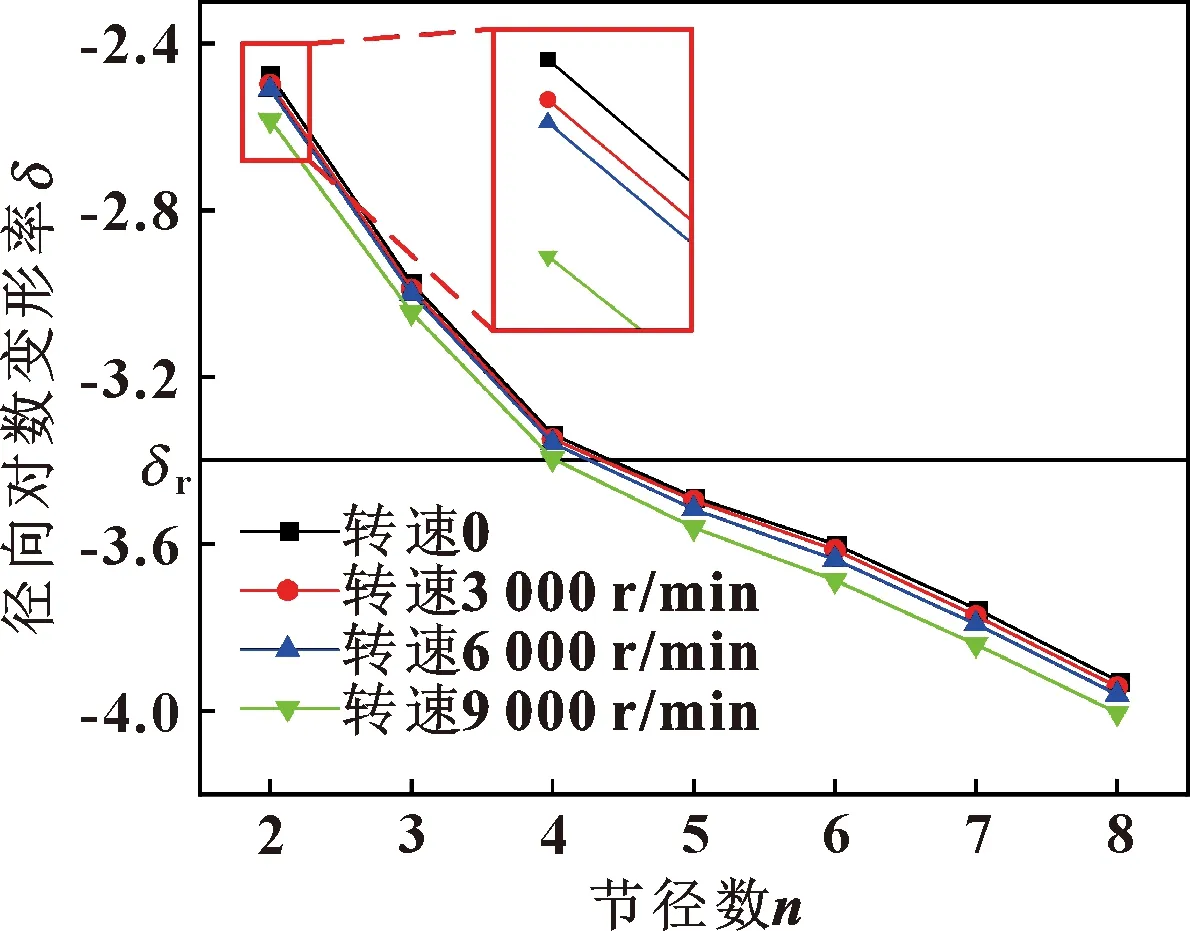
图20 内篦齿环气弹稳定性随转速变化规律Fig.20 The aeroelastic stability of interior labyrinth seal ring versus rotating speed differential
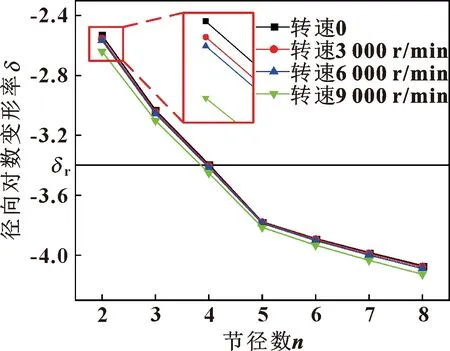
图21 外篦齿环气弹稳定性随转速变化规律Fig.21 The aeroelastic stability of exterior labyrinth seal ring versus rotating speed differential
3.3 篦齿封严气弹失稳影响机制分析
篦齿封严模态分析是气弹稳定性分析的基础,较高的固有频率可以有效提高篦齿封严气弹稳定性。为研究篦齿封严齿间距、壁厚以及转速对固有频率的影响,分析了不同结构参数和工况下篦齿封严前8阶固有频率。对于确定的物理模型和工况条件,压差Δp、封严长度L以及质量M均为常数,此时该模型某节径振动下是否发生气弹失稳取决于节径数n以及该节径下的固有频率ω,将n2/[(n2+1)·ω2]定义为特征频率ωc。图22给出了特征频率随节径数变化曲线,其中前4阶节径振动对气弹稳定性影响最大。随着节径数的增加,曲线斜率在减小,较低节径斜率变化急剧,故径向对数变形率在低节径时较大且变化剧烈,所以低节径更易失稳,并且通过改变结构参数更容易影响低节径的气弹稳定性。
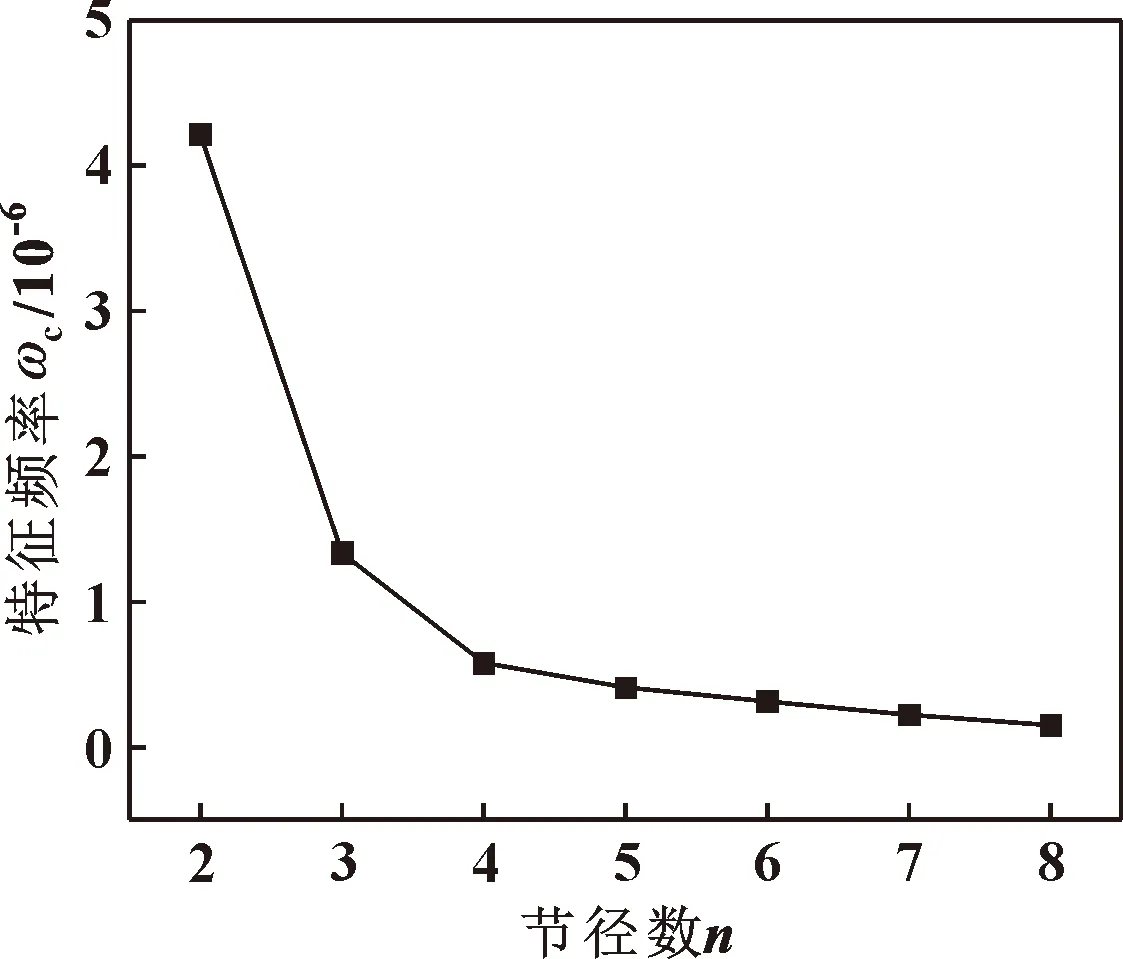
图22 特征数与节径数的关系Fig.22 Relationship between characteristic frequency and the number of nodal diameters
为研究篦齿封严气弹失稳机制,研究了部分典型节径在不同结构参数和工况下气弹稳定性变化规律,如表5所示。

表5 第4节径篦齿封严气弹稳定性Table 5 Aeroelastic stability of labyrinth seal under 4ND
弹性体自身固有频率[19]如式(16)所示。
(16)
联立式(14)(16)化简为
(17)
式中:K为结构刚度;M为图3中转子件整个固体域实际质量。
对于初始结构参数的篦齿封严,在第4节径振型振动下处于临界稳定状态,随着篦齿环齿间距的增加,第4节径振型下的振动转变为气弹失稳状态。由于齿间距的增加会引起封严长度L增加,同时也会引起篦齿封严实际质量和模态质量的增加,三者共同作用导致稳定性下降,封严长度、实际质量和模态质量三者耦合,为此给出了外篦齿环LM/Mω与齿间距之间的关系,如图23所示,将LM/Mω定义为特征长度Lc。随着齿间距的增加,特征长度在增加,根据公式(17),进而引起径向对数变形率的增加,从而导致气弹稳定性的下降。随着篦齿环壁厚的增加,第4节径振型下的振动稳定性得到改善,转变为稳定状态。由于篦齿环壁厚的增加同时会引起薄壁结构篦齿环的刚度、实际质量和模态质量的增加。如图24所示给出了M/Mω随壁厚增加的变化规律,将M/Mω定义为质量比。随壁厚的增加,结构刚度在增加,质量比在降低,综合影响下,根据公式(17)径向对数变形率呈现降低的趋势,从而改善气弹稳定性。
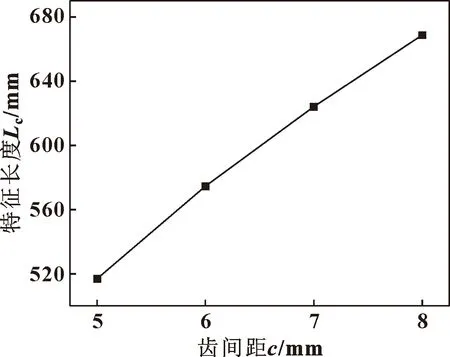
图23 特征长度与齿间距的关系Fig.23 Relationship between characteristic length and cavity width
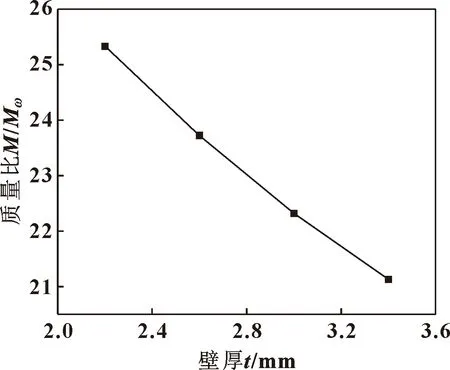
图24 质量比与壁厚的关系Fig.24 Relationship between mass ratio and wall thickness
4 结论
理论分析了篦齿封严结构动力学与气弹稳定性判定公式,建立了篦齿封严气弹稳定性数值求解模型和气弹稳定性求解模型,研究了篦齿环齿间距、壁厚以及转速对篦齿封严固有频率与气弹稳定性的影响规律,得出结论如下:
(1)篦齿封严在发生振动时,相比于高节径,较低的前4节径更易发生气弹失稳,原因在于较低节径具有更高的特征频率,从而具有更高的径向对数变形率。
(2)篦齿封严齿间距的增加会引起特征长度的增加,进而引起径向对数变形率的增加。当齿间距增加时,对内篦齿环径向对数变形率影响较大,径向对数变形率最大升高8.54%,不利于篦齿封严的气弹稳定性。
(3)篦齿封严壁厚的增加,可增加薄壁结构篦齿环的结构抗弯刚度,并降低质量比,在二者的综合作用下,引起径向对数变形率的降低。当壁厚增加时,对外篦齿径向对数变形率影响较大,最大降低7.00%,可有效改善气弹稳定性。
(4)在转子离心力的作用下,增加转速会引起篦齿封严结构刚度的增加,以致固有频率增加,对气弹稳定性影响较小。
