槽参数对高温密封汽液固流动特性及性能的影响*
2023-10-07陈汇龙史迪超陈英健卫泽鹏刘瑞睿
陈汇龙 史迪超 侯 婉 程 谦 陈英健 卫泽鹏 刘瑞睿
(1.江苏大学能源与动力工程学院 江苏镇江 212013;2.安徽江淮汽车集团股份有限公司 安徽江淮 305870)
机械密封广泛应用于旋转式流体输送设备的轴端密封,随着高参数、高效、环保成为工业系统的发展方向,机械密封面临复杂工况和高性能要求的挑战。动压型机械密封作为备受关注和研究的新型密封,其性能与密封端面槽型参数、润滑介质特性和运行工况条件等因素密切相关,尤其是面对含固体颗粒润滑介质及高温汽化问题,亟待深入研究润滑膜汽液固流动特性及密封润滑机制,探索提升密封适应能力的途径[1-2]。
对于动压型机械密封润滑膜含固体颗粒、空化、相变等多相润滑问题,已有诸多国内外学者开展了卓有成效的研究工作。彭旭东等[3]从磨损的角度模拟研究了密封介质内固体颗粒对核主泵用U形槽动压密封的影响,研究发现泄漏量随动压槽根部磨痕数量的增加而呈线性增大。郝木明、李振涛等[4-5]基于JFO空化边界条件研究了槽型、工况参数对螺旋槽密封性能的影响,以及膜厚、表面粗糙度、螺旋槽功用(上游泵送和下游泵送)、螺旋槽开槽位置及空化压力对液膜中空化发生的影响。MA等[6]设计了2种在静环面开设不同组合槽型的机械密封,观察到了不同载荷及转速时槽内出现的空化区域。HUGHES等[7]在相关简化假设情况下提出了间断沸腾模型,对密封液膜相变过程进行了研究。LEBECK[8]提出了涉及相变的混合摩擦模型,对两相的不稳定性进行了较为准确的预测,认为相变使流体膜承载力增大。ETSION等[9]运用热流体动力学方法研究了机械密封间隙液膜沸腾问题,对动静环端面存在少许错位时的液膜相变分析模型进行简化。曹恒超等[10]建立了非接触式机械密封液膜相变模型,仿真模拟了密封液膜相变现象,分析了槽型、工况参数等对液膜相变的影响以及相变区域、相变率等对密封性能的影响。研究认为,对于双列螺旋槽机械密封,外侧螺旋槽内存在较大的相变区域,使压力分布规律产生明显变化,而内侧螺旋槽形成的高压对相变产生了抑制作用,使流体膜呈液相。MIGOUT等[11]针对密封润滑膜蒸发进行研究,发现汽化现象能够有效减小端面温度。陈汇龙等[12-14]采用欧拉多相流模型模拟研究了上游泵送机械密封微间隙液相气核含量、颗粒相物性参数对润滑膜空化的影响关系,应用DPM模型模拟研究了润滑膜内固体颗粒沉积特性;建立了基于黏温效应、牛顿内摩擦效应的密封液膜汽化计算模型,以上游泵送机械密封为对象研究了工况变化对液膜汽化特性及密封性能的影响规律。
综上可见,目前对密封润滑膜流动的研究主要涉及汽(气)液或固液两相问题,对汽液固三相问题的研究很少,对高温工况的研究也较少。为此,本文作者以高温动压型机械密封为研究对象,以水为密封介质,采用Eulerian多相流模型,在考虑介质温度与水的饱和蒸汽压力关系、黏温效应与牛顿流体内摩擦效应的情况下,建立涉及微小固体颗粒和汽化的润滑膜汽液固流动计算模型,研究密封端面槽型参数、工况参数对润滑膜汽液固三相流动特性及密封性能的影响规律,为高温动压型机械密封的研究设计提供一些参考。
1 物理模型
文中以用于高温介质的上游泵送机械密封为具体研究案例,动环端面螺旋浅槽微造型见图1,槽型线采用等角螺线,其表达式[15]为

图1 动环端面螺旋槽造型及几何参数Fig.1 The shape and geometric parameters of the spiral groove on the end face of the moving ring
r=rieφtanθ
(1)
式中:r为槽型线上任一点的极径,mm;φ为槽型线上任一点的极角,(°);θ为槽型线的螺旋角,(°);ri为螺旋槽内半径,mm。
2 数学模型
2.1 基本假设
文中以高温水为密封介质;设进入润滑膜的固体颗粒尺寸服从标准Rosin-Rammler分布,平均直径dmean为2.0 μm,密度为2 200 kg/m3,折合成连续介质的动力黏度μp为0.04 Pa·s,热导率kp为0.27 W/(m·K),比热容Cp为996 J/(kg·K),初始温度设为300 K。为提升润滑膜内流场的计算效率,依据研究对象的特点,对计算模型作以下假设[16]:
(1)固体颗粒、汽泡均视为球形且大小均匀,并将固体颗粒相、汽泡相与液相均看作连续介质;
(2)忽略润滑膜与密封端面之间、三相之间的相对滑移,不计固体颗粒的热辐射;
(3)润滑膜流体为不可压缩;
(4)作为前期研究,暂不考虑密封环的热力变形。
通过液膜流动因子α[6]测算得知,α值小于900/1 600,因此微间隙润滑膜的流态为层流。
2.2 基本方程
由于欧拉多相流模型允许对多个分离但相互作用的相分别进行建模,这些相可以是液相、气(或汽)相或几乎任何组合的固相,且每个相都使用欧拉处理,故根据文中所研究的润滑膜汽液固三相流动特点,采用了ANSYS Fluent软件提供的欧拉模型控制方程,具体包含各相的连续性方程、动量守恒方程及能量守恒方程,具体如下。
(1)连续性方程
液体相:
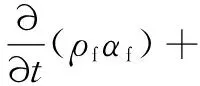
(2)
固体颗粒相:

(3)
汽相输运方程:
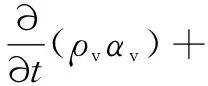
(4)
式中:下标f、s、v分别表示液体相、固体颗粒相和汽相;ρf、αf、Sf分别为液体相的密度、体积分数、源项;ρs、αs、Ss分别为固体相的密度、体积分数、源项;ρv、αv分别为汽相的密度、体积分数,Re、Rc分别为相变过程的蒸发项、冷凝项。
(2)动量守恒方程
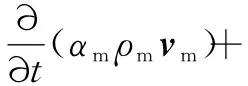

(5)
式中:α为相体积分数,下标m表示混合相,n为相数,下标q表示第q相;gm为混合相重力加速度,m/s2;μm为混合黏性系数,Pa·s;F为体积力,N;p为压力,N;vm为相的速度矢量;Rqm为两相之间的动量交换强度。
(3)能量守恒方程

(6)
式中:hm为相的比焓,J/kg;pm为混合物压力,Pa;k为传热系数;∇(k∇T)为传热引起的能量转移,J;τeff·v为流体黏性耗散能量,J;Qqm为每两相之间的热交换强度;Sh为能量方程的广义源相,包含其他所有热源。
2.3 相变模型
文中研究涉及密封润滑膜内液相高温汽化问题,属温度变化主导的相变过程,故采用在相变问题中应用相对成熟的蒸发冷凝Lee计算模型。
(1)Lee模型
计算式[17]如下:
IfTl>Tsat,
(7)
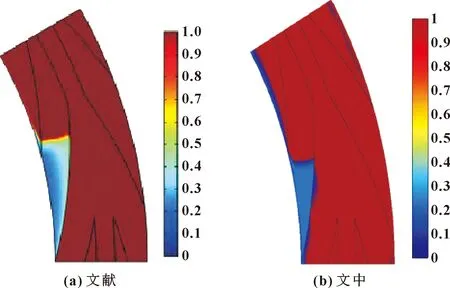
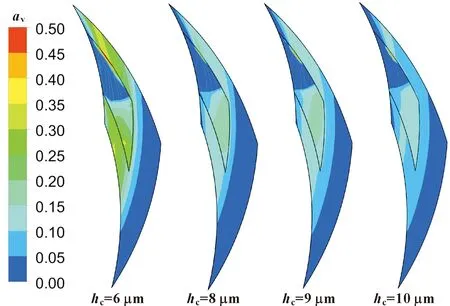
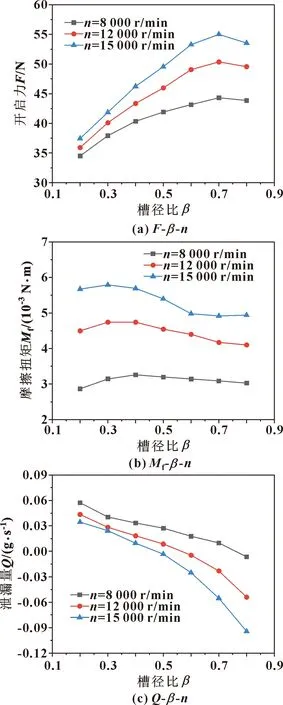
IfTv (8) 式中:Tsat为当地饱和温度;ce为蒸发冷凝系数,通过推导得: (9) 其中,β为适应系数,表示蒸汽分子进入液体表面并被吸附的部分,在近似平衡的条件下趋近于1.0;db为汽泡直径,m;M为摩尔质量,kg/mol;L为潜热,J/kg;R为通用气体常数。 (2)换热系数 鉴于密封润滑膜厚度为微米级尺度,故假设润滑膜与动、静环端面之间的对流换热系数相同并由以下经验公式[18]计算得到: (10) 式中:λf为流体导热系数;Pr为普朗特数,Pr=Cpμ/λf,其中Cp为流体的比热容,J/(kg·K),μ为流体的动力黏度,Pa·s;uf为流体的周向平均速度,uf=(ro+ri)ω/4;ν为流体的运动黏度,m2/s;Lc为密封间隙流体的特征长度,Lc=π(ro+ri),mm。 模型计算采用三维双精度求解器,基于压力速度耦合SIMPLEC算法求解,扩散相梯度差值采用Least Squares Cell Based格式,体积分数计算采用一阶迎风差分格式,动量、能量计算采用二阶迎风差分格式,收敛精度设为1×10-5。润滑膜中水的饱和温度与压力关系、黏温关系采用拟合方程并编译成UDF嵌入Fluent计算模块[19]。计算求解流程图如图2所示。 图2 数值计算流程Fig.2 Numerical calculation process 采用文中的欧拉模型模拟计算文献[1]中密封润滑膜固液两相流,将得到的固体颗粒体积分数与文献[1]中采用混合模型得到的计算结果进行对比,如图3所示。可见,两者的计算结果的吻合性良好,说明文中计算模型对两相流或多相流中固体颗粒分布的计算具有较好的准确性和适用性。 图3 润滑膜固体颗粒体积分数模拟结果对比Fig.3 Comparison of simulation results of solid particle volume fraction in lubricating films 采用文中计算模型对文献[20]的研究对象进行计算,得到润滑膜的压力分布、容积含液率分布对比如图4、图5所示。由图4可见,两者的润滑膜高、低压区域位置比较一致且压力变化规律相似;由图5可见,两者的润滑膜容积含液率分布基本一致。但由于文中模型中汽相与液相具有各自的速度场与温度场,而文献[20]以汽液两相均质混合物计算;另外,文中考虑了润滑膜厚度方向上的温度与压力变化以及汽液两相的表面张力与相间界面面积,故两者的计算结果存在些许差异。对比分析表明文中建立的计算模型对于润滑膜汽化的模拟计算也具有良好的适用性和可靠性。 图4 润滑膜压力分布计算结果对比Fig.4 Comparison of calculation results of lubricating film pressure distribution:(a)literature;(b)this paper 图5 润滑膜容积含液率分布计算结果对比Fig.5 Comparison of calculation results of volumetric liquid content distribution of lubricating film:(a)literature;(b)this paper 文中研究涉及的密封端面几何参数:内半径ri为25 mm、外半径ro为31 mm、槽根圆半径rg为28 mm;工况参数:介质温度T为423 K、介质压力p为0.8 MPa、转速n为5 000~15 000 r/min、膜厚h为4 μm、固体颗粒体积分数为0.2;槽型参数取值范围:螺旋角θ为16°~22°、槽径比β为0.2~0.8、槽宽比γ为0.2~0.8、槽深hc为6~12 μm,槽数Ng为12。密封介质物性参数值见表1。在研究中,除变化量取上述数值区间外,其余相关参数默认值:转速n为12 000 r/min,螺旋角θ为20°,槽径比β为0.5,槽宽比γ为0.5,槽深hc为8 μm。 表1 密封介质物性参数Table 1 Physical parameters of sealing medium 为了能够更有效地利用计算资源,依据润滑膜流场的周期性特点,将计算域选为单周期润滑膜。采用ICEM软件对润滑膜进行网格划分,对螺旋槽区进行网格加密,并进行了网格无关性检验,确定了36万网格方案。计算域边界条件设置为:微间隙液膜设置为静止域,其表面设为静止壁面;螺旋槽内水体设置为旋转域,螺旋槽侧壁面及槽底壁面设为旋转壁面;润滑膜外径侧为压力进口,压力值为介质压力,内径侧为压力出口,压力值为标准大气压力,其余2个侧面满足周期性边界条件。 润滑膜固体颗粒相、汽相分布随槽深变化的云图分别如图6、图7所示。从图6可见,膜内固体颗粒主要分布区域及体积分数随槽深的增大呈快速增大后略有减小变化,槽深为8 μm时出现极大值,相对于槽深低于8 μm而言,槽深高于8 μm时的固体颗粒分布区域及体积分数更大些。从图7可以看出,虽然膜内主要汽化区域随槽深增大的变化不明显,但汽相体积分数随槽深的增大而减小。分析认为,槽深为较小的6 μm时,泵送流通道相对较窄,低温泵送流对槽堰区温度的影响较弱,高温压差流的影响较大,槽堰区汽化程度较高,密封面低压侧固体颗粒的进入受到一定的抑制,颗粒分布区域较小;槽深适度增大至8 μm时,泵送能力增强,槽堰区汽化程度减弱,密封面低压侧固体颗粒进入增多,颗粒分布区域明显增大;槽深进一步增大时,进一步增强了泵送能力,外槽根高压区的影响增大,汽化程度有所降低,槽堰区固体颗粒受到的压力梯度力增大,导致颗粒分布区域有所收缩。 图6 不同槽深时润滑膜固体颗粒分布云图Fig.6 Distribution of solid particles of lubrication film at different groove depths 图7 不同槽深时润滑膜汽相分布云图Fig.7 Distribution of vapor phase of lubrication film at different groove depths 不同转速下润滑膜平均汽相体积分数、固体颗粒体积分数随槽深变化曲线如图8所示。从图8(a)可见,总体上槽深增大润滑膜平均汽相体积分数减小;在转速达到12 000 r/min及以上时,平均汽相体积分数在槽深为8 μm处出现局部极小值,同时,由于高转速下内摩擦温升对汽化的促进作用强于膜压升高对汽化的抑制作用,使平均汽相体积分数随转速升高而有所增大;而转速在8 000 r/min及以下时,小槽深导致的较高汽相体积分数也在槽深8 μm处速降至0附近,并在槽深继续增大时保持低汽化状态。从图8(b)可以看出,润滑膜固体颗粒体积分数总体上随槽深的增大而增大,但同样在槽深为8 μm时出现局部极大值,且转速越高润滑膜固体颗粒体积分数越大,极大值也越大。可见,槽深8 μm是汽相、固体颗粒相出现突变的特征点,在槽深低于8 μm时润滑膜处于较高汽化、较少固体颗粒状态,槽深高于8 μm时则变为相反状态。 图8 润滑膜汽相、固体颗粒相的体积分数随槽深变化规律Fig.8 Variation of the volume fraction of vapor phase(a) and solid particle phase(b)of lubrication film with groove depth 不同转速时汽液固润滑的密封性能参数随槽深的变化曲线如图9所示。从图9(a)可见,转速增大润滑膜开启力增大,但不同转速时开启力随槽深的变化规律有所不同,转速在12 000 r/min及以上时,槽深增大开启力呈近线性增大,且转速越高增速越大;转速低于8 000 r/min时,槽深增大开启力基本不变,仅在转速为8 000 r/min、槽深从6 μm增至7 μm和转速为5 000 r/min、槽深从7 μm增至8 μm时,因润滑膜汽化的快速抑制使开启力出现明显的增大,以及转速为5 000 r/min、槽深11 μm时因固体颗粒体积分数超过了8 μm时的极大值而再现明显增大。结合图7分析认为,润滑膜汽化的快速抑制及固体颗粒含量的突增对高转速时的开启力影响不明显,但对低转速时的开启力影响较大。从图9(b)可看出,槽深、转速变化引起的润滑膜摩擦扭矩变化规律类似于开启力的变化规律,所不同的是转速5 000 r/min时摩擦扭矩随槽深变化较小,只在槽深8~9 μm时略有增大和在槽深11~12 μm时略有下降。从图9(c)可见,低转速(8 000 r/min及以下)时,润滑膜汽化快速抑制和固体颗粒含量突增对应的槽深区间,仍会导致泄漏量的明显较小,但当转速为5 000 r/min、槽深大于11 μm时泄漏量出现增大,说明低转速时,过大的槽深易导致正泄漏量的增大;较高转速(12 000 r/min及以上)时,槽深增大密封泄漏量减小,且在槽深大于9 μm时出现负泄漏,转速越高负泄漏量越大。 润滑膜内固体颗粒相、汽相分布随槽宽比变化的云图分别如图10、图11所示。由图10可见,固体颗粒主要分布在槽堰区内径附近区域,其他区域的分布很少;槽宽比不同时固体颗粒主要分布区域向外槽根扩展程度不同,槽宽比为0.3时分布区域小且周向分布较均衡,槽宽比增至0.5时分布区域基本覆盖了整个槽堰区,达到最大范围,继续增大槽宽比时分布区域向内径侧有所收缩且周向分布趋于不均衡。由图11可见,润滑膜汽化主要发生在外槽根至迎风侧区域及堰区;槽宽比为0.3时,润滑膜整体汽化程度很低,槽宽比增大时汽化程度升高,当槽宽比增至0.6时汽化区域和程度明显增大,但继续增大槽宽比时汽化程度略有下降。对云图分析认为,较小槽宽比时槽区狭长,虽然泵送量小、低压区范围小,但较窄的外槽根聚压效果较好并形成高压区,因此进入槽区的固体颗粒较少、汽化程度低;槽宽比增至0.5时,虽然泵送量增大、低压区也增大,但增宽的外槽根聚压效果减弱,且在膜温升高导致液相黏度下降情况下,外槽根不仅膜压升高有限,而且形成汽化泡集聚,槽堰区汽化程度升高,但因固体颗粒含量的增大对汽化产生一定的抑制,故汽化程度没有达到最高状态;槽宽比继续增大时,槽区加宽,槽内流动趋于复杂化甚至出现回流,固体颗粒分布减少且周向不均衡,对汽化的抑制减弱,同时外槽根聚压效果进一步减弱,使汽化程度进一步升高;但过宽的槽区,虽然外槽根聚压效果差,但堰区狭窄、汽化区域小且内径侧低温介质对槽区的影响范围加大,汽化程度反而有所下降。 不同转速时润滑膜汽相和固体颗粒相的体积分数随槽宽比变化的曲线如图12所示。从图12(a)可见,槽宽比增大时,润滑膜平均汽相体积分数呈先增大后减小变化,其最大值对应的槽宽比为0.7;转速越高,内摩擦温升越大,平均汽相体积分数越大。从图12(b)可知,转速增大润滑膜固体颗粒体积分数也增大,但不同转速下均在槽宽比为0.5时出现最大的固体颗粒体积分数;槽宽比高于0.7后,转速为8 000、12 000、15 000 r/min时固体颗粒体积分数分别出现明显下降、微弱下降、明显增大的变化。可见,槽宽比过大时槽堰区汽化加剧,汽液固流动趋于复杂化和不稳定,故采用小于0.5的槽宽比为好。 不同转速时密封性能参数随槽宽比变化的曲线如图13所示。从图13(a)可见,槽宽比增大时润滑膜开启力呈先增大后减小变化,即开启力存在最大值且所对应的槽宽比在0.3~0.4之间;随转速升高开启力增大。从图13(b)可见,总体上摩擦扭矩随槽宽比增大、转速降低而减小。从图13(c)可见,除了低转速、高槽宽比外,总体上槽宽比对泄漏量的影响不大,在槽宽比为0.3~0.4之间时可获得较小的泄漏量;转速升高正泄漏量减小,但转速高于12 000 r/min时,会出现负泄漏。可见,选择0.3~0.4之间的槽宽比,可获得更优的密封综合性能。 润滑膜固体颗粒相、汽相分布随螺旋角变化的云图分别如图14、图15所示。由图14可见,螺旋角增大时固体颗粒分布规律的变化不明显,仅有固体颗粒主要分布区域随螺旋角增大而向槽堰区略为收缩,这是因为大螺旋角螺旋槽的泵送能力弱于小螺旋角螺旋槽,固体颗粒在迎风侧获得的泵送能量相对较弱,到达外槽根甚至附近坝区固体颗粒减少。由图15可见,润滑膜的汽化区域和程度随螺旋角的增大而增大,在螺旋角为16°时,润滑膜内几乎不产生汽化,说明此时螺旋槽泵送效应明显,膜压较高,润滑膜受内径侧低温介质的影响较大,受外径侧高温介质的影响较弱,槽堰区膜温较低,汽化不易发生;螺旋角增大时,螺旋槽泵送效应减弱,膜压降低,润滑膜受外径侧高温介质的影响增强,膜温升高,槽堰区汽化程度提高。 图14 不同螺旋角时润滑膜固体颗粒分布云图Fig.14 Distribution of solid particle of lubrication film at different helix angles 图15 不同螺旋角时润滑膜汽相分布云图Fig.15 Distribution of vapor phase of lubrication film at different helix angles 不同转速时润滑膜汽相和固体颗粒相的体积分数随螺旋角变化的曲线如图16所示。从图16(a)可以看出,转速为8 000 r/min时只有当螺旋角增至20°以上时润滑膜才开始出现汽化,转速升高后,汽化加剧,且润滑膜平均汽相体积分数随螺旋角增大而呈近线性增大。从图16(b)可见,固体颗粒体积分数随螺旋角变化的规律与转速有关,转速分别为8 000、12 000、15 000 r/min时,固体颗粒体积分数随螺旋角增大分别呈缓慢增大、缓慢减小、明显减小的变化规律,但总体上固体颗粒体积分数随螺旋角变化的幅度较小。可见,从抑制汽化的角度看,选取较小的螺旋角更有利。 图16 润滑膜汽相、固体颗粒相的体积分数随螺旋角变化规律Fig.16 Variation of the volume fraction of vapor phase(a) and solid particle phase(b)of lubrication film with helix angle 不同转速时密封性能参数随螺旋角的变化规律如图17所示。从图17(a)可见,螺旋角增大时润滑膜开启力减小,转速升高时开启力增大,且转速升高时开启力对螺旋角的变化更敏感。从图17(b)可以看出,螺旋角变化对摩擦扭矩的影响较小,但转速升高摩擦扭矩增大。从图17(c)可知,螺旋角增大时正泄漏量增大,转速为12 000 r/min、螺旋角小于17°和转速为15 000 r/min时出现负泄漏,且随螺旋角增大负泄漏量减小。综合分析认为,转速在8 000 r/min以下时选用16°~20°的螺旋角,转速高于8 000 r/min时选用16°左右的螺旋角,密封性能更优。 图17 不同转速时密封性能随螺旋角变化规律Fig.17 Variation of sealing performance with helix angle under different rotational speed:(a)F-θ-n;(b)Mf-θ-n:(c)Q-θ-n 不同槽径比时润滑膜固体颗粒相、汽相分布云图分别如图18、图19所示。从图18可见,内径侧固体颗粒分布数量最多并向外径侧方向递减;槽径比增大时固体颗粒主要分布区域扩大,槽径比达到0.8时固体颗粒主要分布区几乎覆盖了整个密封面。说明槽堰区始终是固体颗粒主要分布区,槽径比增大,槽堰区扩展,固体颗粒主要分布区域也随之扩展。从图19可以看出,槽堰区及附近坝区为汽化主要发生部位,槽径比增大时汽相主要分布区域增大,槽区低汽化区也向外槽根方向扩展,当槽径比达到0.8时主要汽化区已延伸至密封面外径侧;虽然在槽径比为0.2时主要汽化区域较小,但在槽迎风侧内径附近及堰区靠近坝区部位却出现了高汽化。说明槽径比增大使槽区延长,泵送效应和动压效应导致的槽堰低压区随之扩大,内摩擦温升的影响也因槽堰区增大而加大,扩展了主要汽化区域,同时槽区低温泵送流区域也随之延伸;槽径比过小时,槽型短,泵送流弱,压差流影响强,高温密封介质对膜温的影响强烈,导致槽堰区局部出现高汽化。 图18 不同槽径比时润滑膜固体颗粒分布云图Fig.18 Distribution of solid particle of lubrication film under different groove diameter ratios 图19 不同槽径比时润滑膜汽相分布云图Fig.19 Distribution of vapor phase of lubrication film under different groove diameter ratios 不同转速时润滑膜汽相、固体颗粒相的体积分数随槽径比的变化规律如图20所示。从图20(a)可以看出,低槽径比0.2时,增大转速能够增强动压效应,降低汽化程度;当槽径比在0.3及以上时,槽堰区面积增大,转速较高时平均汽相体积分数增大且随槽径比的增大而增大,转速较低时内摩擦温升对槽堰区汽化的影响较小,转速为8 000 r/min且槽径比高于0.4时,出现了平均汽相体积分数为0的现象。从图20(b)可见,固体颗粒体积分数随槽径比、转速的增大而增大。分析认为,转速较高时选用较小的槽径比、转速较低时选用较大的槽径比,对抑制汽化更有利。 不同转速时密封性能参数随槽径比的变化规律如图21所示。从图21(a)可见,槽径比增大时润滑膜开启力呈先增大后略有减小变化,开启力最大值对应的槽径比为0.7。从图21(b)可见,槽径比增大时摩擦扭矩呈先略有增大后减小变化,最大摩擦扭矩对应的槽径比为0.3~0.4之间。从图21(c)可以看出,槽径比增大时密封正泄漏量减小,高转速、高槽径比时易出现负泄漏且随转速、槽径比的增大而增大。兼顾密封性能、汽化特性和固体颗粒分布的分析认为,选用0.6左右的槽径比时密封综合性能较好。 图21 不同转速时密封性能随槽径比变化规律Fig.21 Variation of sealing performance with groove diameter under different rotational speed:(a)F-β-n;(b)Mf-β-n:(c)Q-β-n 在文中研究的工况参数条件下,得到以下结论: (1)润滑膜内固体颗粒主要分布在槽堰区,固体颗粒体积分数随槽参数变化规律为:随槽深、槽径比的增大而增大,但槽深为8 μm时出现局部极大值,且转速越高体积分数越大、极大值越大;不同转速下均在槽宽比为0.5时出现最大值;较低转速时随螺旋角增大而缓慢增大、较高转速时随螺旋角增大而明显减小。 (2)润滑膜平均汽相体积分数随槽参数变化规律为:随槽深的增大而减小,但槽深8 μm时出现局部极小值(较高转速)或速降至0附近(较低转速);槽宽比为0.7时出现最大值;随螺旋角的增大而增大;槽径比低于0.3时随转速增大而减小,槽径比在0.3以上时随转速、槽径比的增大而增大且转速低于8 000 r/min时汽化微弱甚至消失。 (3)较高转速时润滑膜开启力随槽深增大而增大,较低转速时开启力对槽深变化不敏感且仅在汽化速降对应槽深开启力出现局部增大,槽宽比为0.3~0.4或槽径比为0.7时开启力出现最大值;开启力随螺旋角增大而减小且转速越高对螺旋角的变化越敏感;摩擦扭矩受槽深、螺旋角变化的影响较小,随槽宽比增大而减小,在槽径比为0.3~0.4时最大;转速较低时过大的槽深易导致正泄漏量的增大,转速较高时槽深增大密封正泄漏量减小甚至出现负泄漏,槽宽比为0.3~0.4时泄漏量较小,螺旋角增大时正泄漏量增大或负泄漏量减小,槽径比增大时正泄漏量减小。 (4)综合分析可得,槽深8 μm时润滑膜汽相、固体颗粒相出现突变,槽深低于8 μm时汽相强、固体颗粒相弱,槽深高于8 μm时则相反;选用9 μm左右的槽深、0.6左右的槽径比、16°~20°的螺旋角、0.3~0.4的槽宽比时对密封性能有利;采用8 μm以上的槽深、小于0.5的槽宽比、转速较高时选用较小槽径比、转速较低时选用较大槽径比对抑制汽化更有利。2.4 计算方法
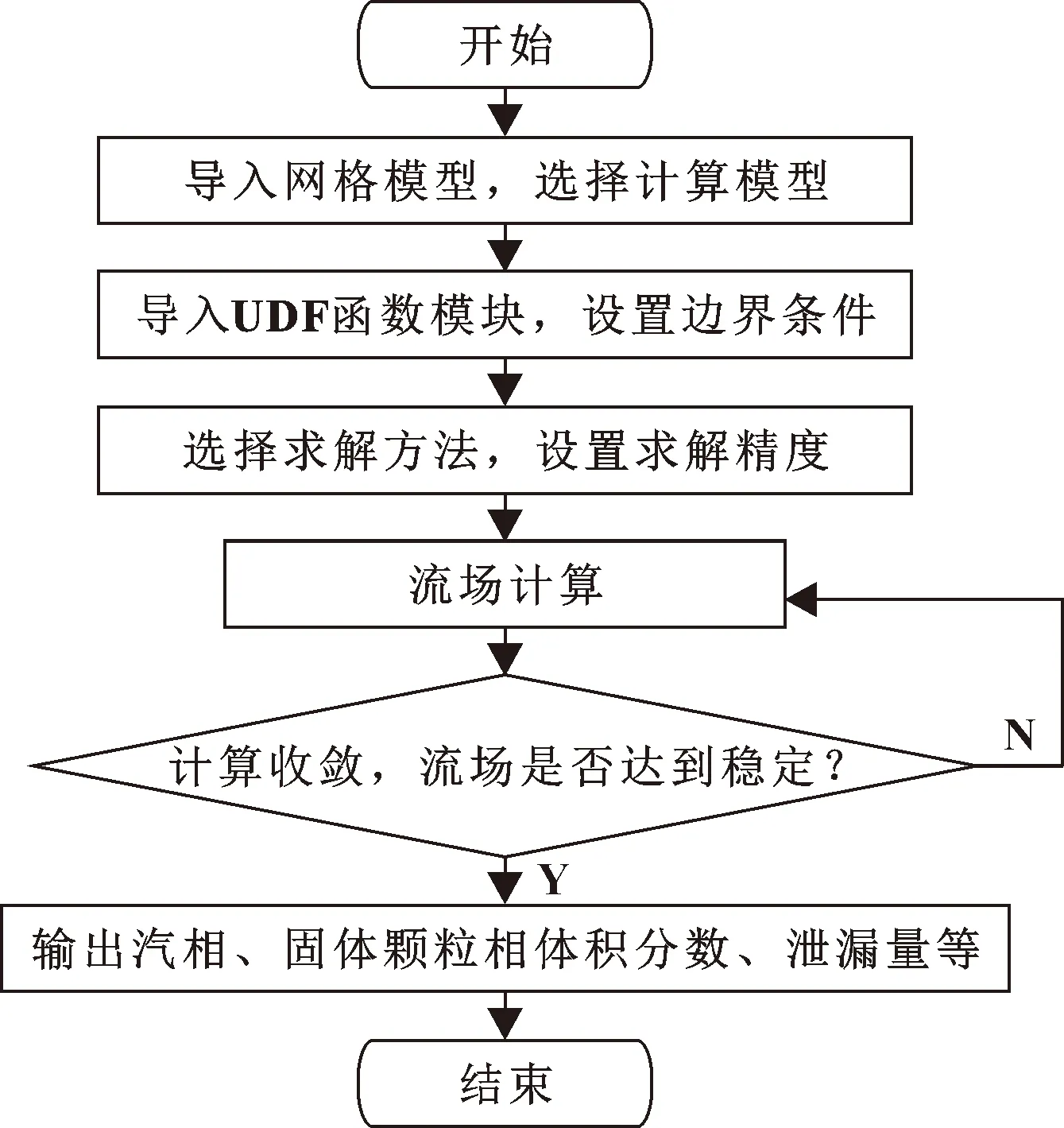
2.5 模型有效性验证


3 算例简介

4 计算结果及分析
4.1 汽固相特性及密封性能随槽深的变化分析


4.2 汽固相特性及密封性能随槽宽比的变化分析
4.3 汽固相特性及密封性能随螺旋角的变化分析




4.4 汽固相特性及密封性能随槽径比的变化分析


5 结论
