竖直小通道内弹状流气弹长度的计算模型

闫超星，阎昌琪，孙立成，王 洋，张小宁

(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001)

鉴于紧凑式换热器的发展需求，小通道内部的两相流动特性得到了广泛的关注。由于弹状流内部气弹和液弹互相尾随交替出现，造成了通道内很大的密度差和流体的可压缩性，易产生流动不稳定性，因此，针对弹状流的实验和理论研究备受国内外学者的关注[1-3]。

对以往的研究总结发现，学者们大都关注气弹上升速度，且提出了较为准确的计算模型，但针对气弹长度的研究仅给出了实验现象和其影响因素，关于气弹长度的计算模型还十分有限，且不完善。气弹长度关系着气液相的分布情况，进而影响传热和阻力特性，此外气弹长度与两相流型间的转变密切相关。因此，有必要建立小通道内气弹长度的计算模型，为今后的研究和工程应用提供技术支持。

1 实验系统

1.1 实验装置及实验内容

实验以空气和水为工质，在常温、常压条件下进行，实验过程中空气和水均保持在20～22 ℃。图1为实验回路示意图。整个实验装置由供水系统、供气系统、实验段、数据采集系统和高速摄像系统5部分组成。实验段为有机玻璃矩形通道，截面尺寸为3.25 mm×43 mm，总长2 m。实验数据测量和采集系统详见文献[4]。高速摄像系统由高速摄像仪、光源和计算机组成。实验中采用Photron公司的FASTCAM SA5型高速摄像仪垂直于实验段宽边进行拍摄，以漫射的背光为光源。图像拍摄处位置距通道入口986 mm，流动已充分发展。

气液流量均通过调节阀来调节，两相混合物流经实验段后，进入气水分离器，在其内部依靠重力自然分离。实验过程中，固定水流量，气流量由小到大依次调节，待每个工况稳定后，记录实验数据，完成1个循环；然后再改变水流量，进行下组实验。

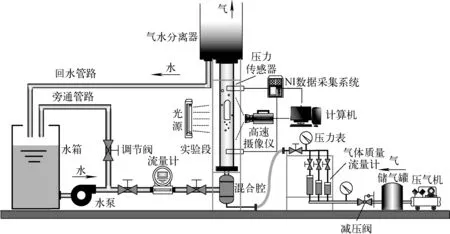
图1 实验回路示意图

1.2 图像处理

图像处理前首先确定标度因子γ。实验段宽边尺寸已知，可通过计算其图像像素点的方式确定γ：

(1)

图像处理过程示于图2。图2a、b和c分别代表n1帧、n2帧和n3帧对应的图像。由图2a、b得到气弹上升速度，再由图2a、c确定的时间间隔得到气弹长度Lb：

Lb=γΔx(n3-n1)/(n2-n1)

(2)

图2 实验图像处理过程

式中，Δx为n2帧与n1帧图像气弹头部界面沿轴向的位移。需指出，窄矩形通道内弹状流的气弹长度具有很大随机性，即使同一流动工况下，流过的气弹长度也会有差异，这体现了两相弹状流的流动不稳定性。为减小主观测量误差，每个气弹重复测量10次，对每个工况下15个气弹进行处理后取平均值。

2 气弹长度模型

竖直通道内弹状流物理模型示于图3。图3中，h为距气弹头部的距离，α(h)和αb分别为距气弹头部h处和气弹尾部的局部空泡份额，ub为气弹上升速度，j为两相折算速度，ufb为液膜末端的平均流速，wb和w分别为气弹宽度(或直径)和通道宽度(或直径)。

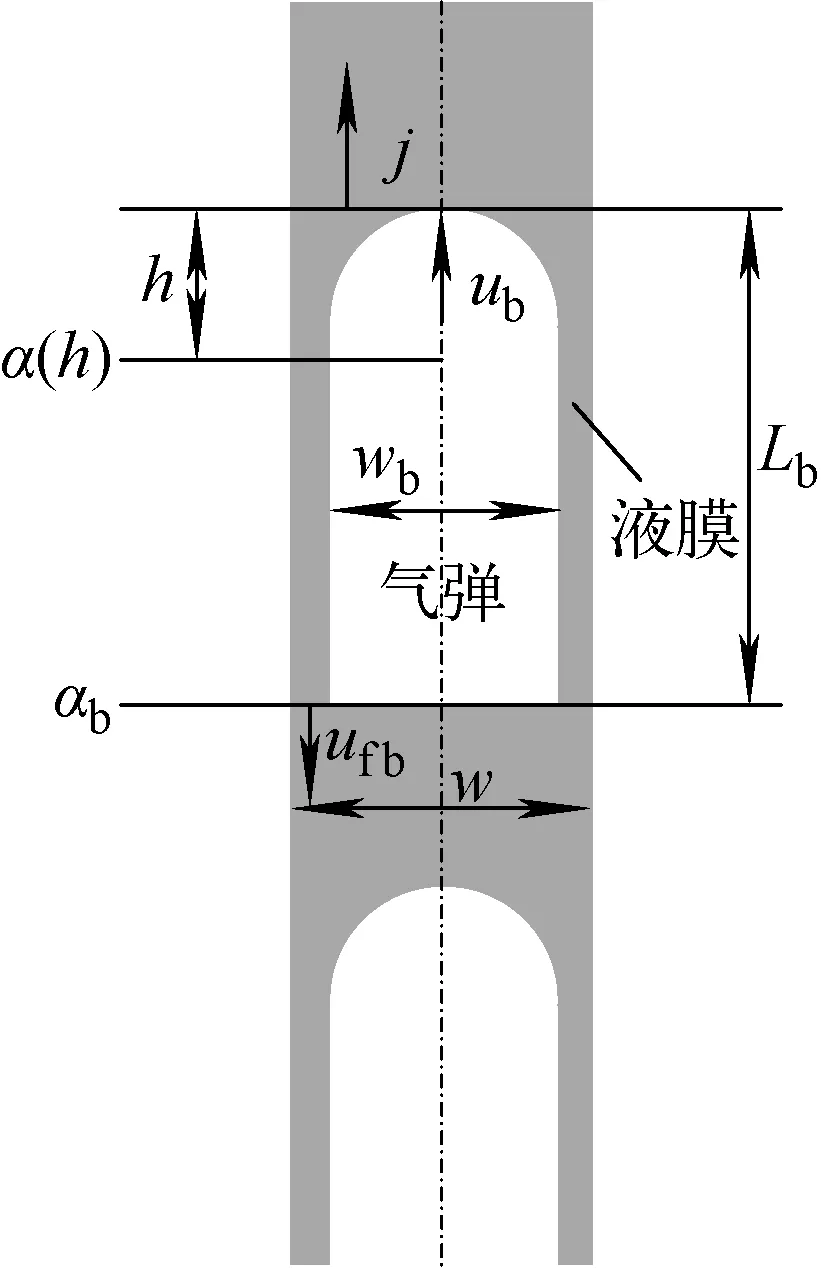
图3 竖直通道内弹状流物理模型

Mishima等[5]针对圆形通道内弹状流应用伯努利方程，得到距气弹头部h处的α(h)：

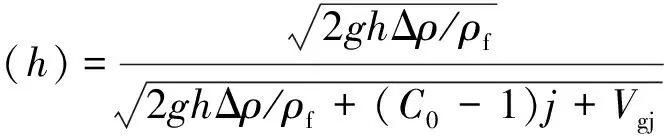
(3)

Xu等[6]和Hibiki等[7]将式(3)应用于矩形通道，其中分布参数C0和漂移速度Vgj分别采用下式计算：

(4)

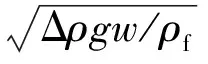
(5)

式中：ρg、ρf和Δρ分别为气、液相密度和两相密度差；s和w分别为通道窄边和宽边尺寸。

Hibiki等[7]认为距气弹头部某一位置处，气弹周围液膜所受的重力与其受到的壁面剪切力相等，此时液膜的流动已充分发展。在此位置以下，向下流动的液膜与向上流动的液弹混合，液膜减速直至不再向下流动，液相搅混剧烈导致此处液膜不稳定，气液界面的扰动将会打断气弹。矩形通道内，贴近宽边处的液膜很薄，与窄边处的液膜厚度相比可忽略，但宽边处的液膜同样受到壁面剪切力的作用；圆形通道内，气弹周向液膜均匀分布。矩形通道和圆形通道内液膜的简化模型示于图4。假设同一横截面上气弹周围液膜速度相等，本文以矩形通道为例进行推导。

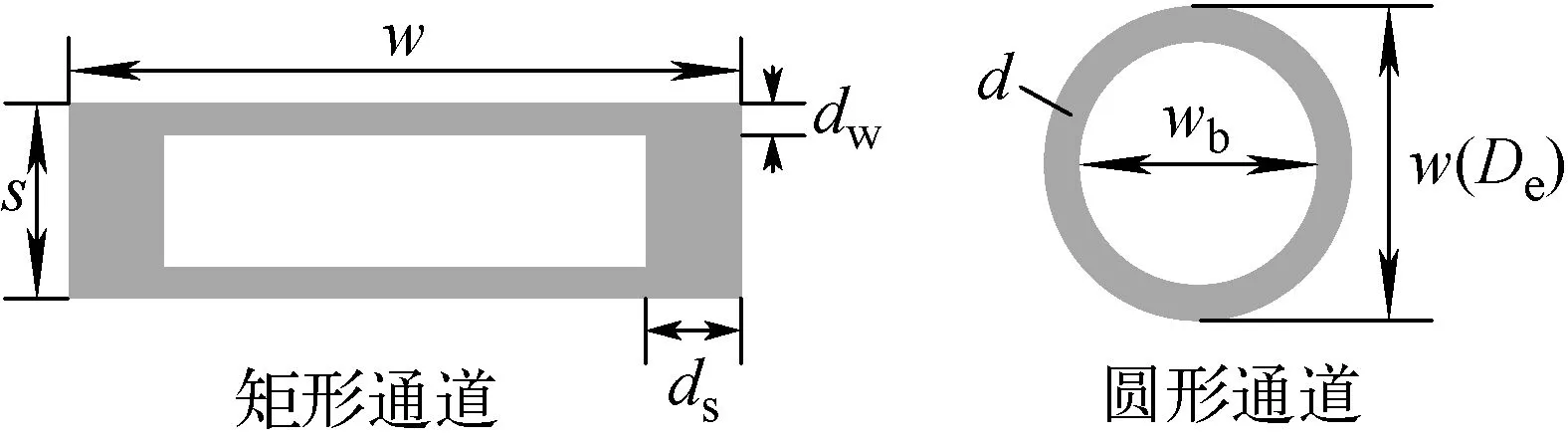
图4 弹状流液膜简化模型

对液膜受力分析可知[6]：

Δρgws(1-αb)dz

(6)

其中：dz为选取液膜微元段沿轴向的长度；f为壁面摩擦系数，其计算式如下：

(7)

其中：De为通道的当量直径；υf为液相运动黏度；层流区n=1，湍流区n=0.25。Mishima等[5]提出，由于液膜内部存在小气泡，且该处液膜紧靠气弹尾部，液相搅混剧烈，因此该处液膜的流动用湍流模型更接近实际情况，本文暂取n=0.25。

Shah等[8]提出了计算矩形通道内单相层流区摩阻系数的关系式：

λ=CflRe-1=96(1-1.355 3ε+1.946 7ε2-

1.701 2ε3+0.956 4ε4-0.253 7ε5)

(8)

其中：λ为单相摩阻系数；ε为矩形通道横截面的窄边与宽边之比，即s/w。

Sadatomi等[9]提出了考虑通道几何形状的湍流摩阻系数关系式：

Cft=Cft0[(0.015 4Cfl/Cfl0-0.012)1/3+0.85]

(9)

式中，Cfl0=16和Cft0=0.079分别为圆管内层流区和湍流区的摩阻系数。通过式(8)及(9)计算矩形通道内层流区和湍流区单相摩阻系数。将式(7)代入式(6)得到气弹尾部液膜的平均速度：

(10)

此外，ufb还与αb存在以下关系[5]：

ufb=(αbub-j)/(1-αb)

(11)

又由漂移流模型可知：

ub=C0j+Vgj

(12)

结合式(10)～(12)可得：

(13)

观察式(13)可发现，该式为计算αb的1个迭代关系式，并不能直接得到计算αb的表达式，因此，需对等式右边1-αb的指数形式进行简化处理，即：

≈β(1-αb)

(14)

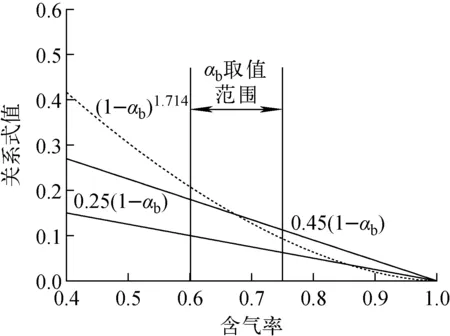
图5 简化关系式验证

当n=0.25、β分别取0.25和0.45时，式(14)两侧计算结果的逼近情况如图5所示。实验获得的气弹宽度与通道宽度的比值大多位于0.6～0.75范围内，窄矩形通道内可近似认为αb等同于气弹宽度与通道宽度的比值，因此，只要保证式(14)左右两边关系式在αb处于0.6～0.75范围内具有较好的一致性即可。通过Mishima等[10]的实验观察和Wilmarth等[11]基于电导探针对液膜厚度的实验研究，发现宽边处的液膜与窄边处相比可忽略，Hibiki等[7]得出当窄边宽度小于2.4 mm时宽边处液膜可忽略。随矩形通道窄边宽度的减小，气弹受到壁面挤压作用越明显，气弹宽度占通道宽度的比例增大。以窄边尺寸2.4 mm为界，当s≥2.4 mm时，β=0.45；当s<2.4 mm时，β=0.25。

将式(14)代入式(13)可得：

αb=(j+β((De/υf)-nCfρf(w+s)/

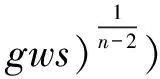
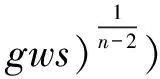
(15)

根据式(3)可得，距气弹头部Lb处的局部空泡份额αb为：

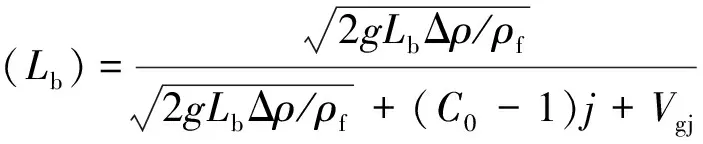
(16)

结合式(15)和(16)可得：

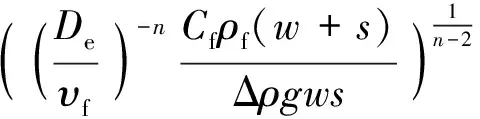
(17)

从而得到气弹长度的关系式为：

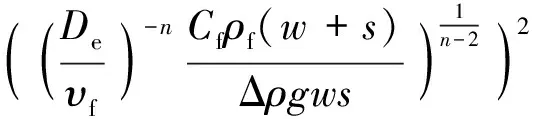
(18)

其中：n=0.25；s≥2.4 mm时，β=0.45；s<2.4 mm时，β=0.25。

圆形通道与矩形通道的机理相同，本文简化推导过程，得到圆形通道计算关系式：

(19)

式(18)和(19)适用于竖直条件下常温绝热空气-水两相弹状流动。

3 结果分析与讨论

3.1 气弹长度的影响因素

观察式(18)和(19)发现，对于给定的流体物性参数，气弹长度仅与通道尺寸和流动状况(j、Cf)相关，实验条件下Cf变化十分有限。因此，本文仅讨论通道尺寸和两相折算速度对气弹长度的影响。以矩形通道为例，图6示出不同高宽比ε时气弹长度随两相折算速度j的变化趋势。由图6可知，气弹长度随高宽比及两相折算速度的增加而增大。

3.2 计算模型的验证

为验证计算模型的实用性，将本文及Mishima等[10]和Cheng等[2]的实验数据与计算值进行对比，结果示于图7。所采用的实验数据列于表1，实验工质均为水和空气，包括矩形和圆形通道。平均绝对误差(MAE)定义为：

∑

(20)

其中：m为实验数据点数；(Lb)pred和(Lb)exp分别为气弹长度预测值和实验值。

对于当前实验数据，计算模型的MAE为26.8%，而对Mishima等和Cheng等全部实验数据的MAE为34.9%，说明计算模型具有较好的适用性。模型对Mishima等的40 mm×1.07 mm通道的实验数据预测效果稍差，可能是模型中认为气弹周向液膜的流速相等引起，因窄边仅为1.07 mm的矩形通道内宽边液膜流动受到抑制，加剧了宽边与窄边液膜速度的不均匀程度，与模型假设存在一定偏差。模型的定性尺寸为表1列出的通道尺寸，需指出，小通道气弹长度的模型十分有限，对其他通道尺寸的适用性有待进一步验证，本文只是提供分析气弹长度的一种方法。

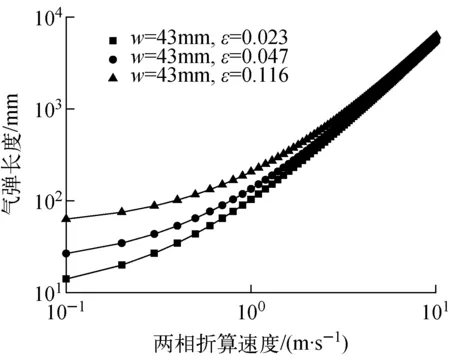
图6 高宽比ε对气弹长度的影响

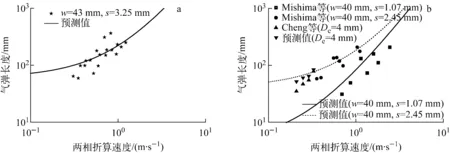
a——本文实验数据；b——公开发表文献的实验数据

表1 气弹长度实验数据

4 结论

通过对弹状流液膜的受力分析，结合漂移流模型建立了小通道内气弹长度的计算模型，并最终给出了气弹长度的计算关系式。通过可视化实验数据及公开发表文献中数据对计算方法进行了评价。计算模型对本实验段的平均绝对误差为26.8%，对Mishima等和Cheng等实验数据的平均绝对误差为34.9%；对于尺度为1 mm左右的小通道，模型的预测精度低于2 mm以上的通道。

参考文献：

[1] 夏国栋，周芳德，胡明胜. 倾斜上升弹状流中Taylor气泡运动速度研究[J]. 化学工程，1997，25(5)：36-41.

XIA Guodong, ZHOU Fangde, HU Mingsheng. Study on the velocity of Taylor bubble in inclined upward slug flow[J]. Chemical Engineering, 1997, 25(5): 36-41(in Chinese).

[2] CHENG T W, LIN T L. Characteristics of gas-liquid two-phase flow in small diameter inclined tubes[J]. Chemical Engineering Science, 2001, 56(21-22): 6 393-6 398.

[3] BHUSAN S, GHOSH S, DAS G, et al. Rise of Taylor bubbles through narrow rectangular channels[J]. Chem Eng J, 2009, 155(1-2): 326-332.

[4] 王广飞，阎昌琪，孙立成，等. 窄矩形通道内两相流动压降特性研究[J]. 原子能科学技术，2011,45(12)：1 331-1 336.

WANG Guangfei, YAN Changqi, SUN Licheng, et al. Resistance characteristics of two-phase flow through narrow rectangular duct[J]. Atomic Energy Science and Technology, 2011, 45(12): 1 331-1 336(in Chinese).

[5] MISHIMA K, ISHII M. Flow regime transition criteria for upward two-phase flow in vertical tubes[J]. Int J Heat Mass Transfer, 1984, 27(5): 727-737.

[6] XU J L, CHENG P, ZHAO T S. Gas-liquid two-phase flow regimes in rectangular channels with mini/micro gaps[J]. Int J Multiphase Flow, 1999, 25(3): 411-432.

[7] HIBIKI T, MISHIMA K. Flow regime transition criteria for upward two-phase flow in vertical narrow rectangular channels[J]. Nuclear Engineering and Design, 2001, 203(2-3): 117-131.

[8] SHAH R K, LONDON A L. Laminar flow forced convection in ducts: A source book for compact heat exchanger analytical data[M]. New York: Academic Press, 1978.

[9] SADATOMI M, SATO Y, SARUWATARI S. Two-phase flow in vertical noncircular channels[J]. Int J Multiphase Flow, 1982, 8: 641-655.

[10] MISHIMA K, HIBIKI T, NISHIHARA H. Some characteristics of gas-liquid flow in narrow rectangular ducts[J]. Int J Multiphase Flow, 1993, 19(1): 115-124.

[11] WILMARTH T, ISHII M. Interfacial area concentration and void fraction of two-phase flow in narrow rectangular vertical channels[J]. J Fluids Eng, 1997, 119(4): 916-922.