基于多项式曲面拟合的新能源最大发电能力评估

2023-10-07姚丹阳

电力系统及其自动化学报 2023年9期

张艳，顾盼，姚丹阳

（国网经济技术研究院有限公司，北京 102209）

对新能源发电能力进行准确预测是降低电力系统不确定性影响的有效手段[1]，但以往研究的重点为如何预测即时功率，而不是当时气象条件下某种运行方式的最大可能发电功率，即发电能力边界。获知新能源发电能力边界是计算新能源可用调频容量的前提条件之一，对电力系统频率稳定控制具有重要作用。准确的新能源最大发电能力预测对于合理确定调度计划和确保电网安全经济运行具有重要意义。

新能源发电主要指风力、光伏等发电出力具有波动性和不确定性的新型能源发电形式[2]。本文主要以风电为例进行介绍，其相关研究思路和模型构建方法也同样适用于其他新能源发电形式。当前，针对风电场最大发电能力的研究尚不多见，对于其研究策略及学习算法的选择，现有的风力发电功率预测方法具有一定的借鉴意义。现有的风电功率预测方法主要分为物理预测法、统计预测法和组合预测法[3]。

风电功率物理预测法是通过建立物理模型，模拟风电场风能资源分布及风能资源输出功率转化过程的预测方法。文献[4]通过综合定量分析上下游风电机组轴间距离、轴间偏向、高度差，针对不同风速下上游风电机组尾流效应对下游风电机组输出功率的影响，给出上下游风电机组输出功率比值与相关位置参数的定量关系式。文献[5]通过风场物理仿真模型优化布局，从而提高风能的合理利用率，增加风电场的输出功率。文献[6]在建立风电机组物理预测模型时，通过设立功率影响因子来量化地形、风电机组布置对风电场功率的影响。如果利用物理仿真直接对最大输出功率进行计算，因风电场各风机参数较多，计算困难度较大，风机出力的准确性也无法保证。

风电功率统计预测法是一种基于数据驱动的方法，常用的风电功率统计预测方法有时间序列模型[7]、前馈神经网络[8-9]、支持向量机SVM（support vector machine）[10]和径向基函数神经网络[11]。文献[7]以时间序列分析为基础，使用自回归滑动平均模型对获取的有序随机数据集进行分析，基于D-S证据理论对模型进行参数修正。文献[8]建立了反向传播BP（back propagation）神经网络预测模型，先对风速进行预测，根据得出的最优风速预测值，进一步对风电功率进行预测。文献[9]应用弹性BP神经网络算法和Levenberg-Marquardt BP 神经网络算法两种改进算法，并与基本BP 神经网络算法的预测结果进行比较。文献[10]采用布谷鸟搜索算法先确定SVM的惩罚因子和核函数参数最佳值，再利用SVM对历史数据进行训练。文献[11]在剔除了异常数据的基础上，基于径向基函数神经网络对历史数据进行预测。统计预测法与本文所提的模型都运用了机器学习的智能算法，但本文所进行的特征工程及输出变量均与统计预测法中描述的大不相同。

风电功率组合预测法是以一定的组合策略将不同统计预测法的计算结果集成，以便获得更优的预测值。在实际工程中常用的组合预测包括集成平均组合预测法[12]和线性回归组合法[13]。文献[12]利用改进粒子群优化算法和蝙蝠算法组合选取SVM 的最优参数，建立了SVM 预测模型，同时又建立了基于自适应噪声原理的集成经验模态分解法，最终采用集成平均组合法建立了SVM 和经验模态分解法的组合预测模型。文献[13]根据均方根误差、平均绝对误差、平均相对误差最小原则选择3个最优单项预测模型，然后利用灰色关联度分析法确定每种组合模型的权重系数，最终可得到优化模型。

综上所述，本文采用数据驱动的统计预测法建立模型，对不同气象条件下风电场的最大发电能力进行计算评估。首先，对影响风电出力的气象资源信息关键特征变量进行关联性分析，筛选出两个相关性最显著的特征变量；然后，基于关键特征变量（即风电场出力的三维散点图）对原始数据集进行最大化筛选和归一化处理，以便构建更为高效的学习样本集，提高风电场最大发电能力回归学习的准确性。

1 基于特征工程的发电能力分析

特征工程使原始数据经过特征选择和数据预处理等过程，更高效地应用于预测模型，提高模型的预测精度。在搭建新能源最大发电能力计算模型时，历史数据信息的可靠性和关键性参数的完备性对模型的准确性至关重要，特征和数据的优良决定了预测模型性能的上限[14]。本文在对多源信息进行特征分析时，采用皮尔逊相关系数选择关键特征参数[15]，并根据最大化的目标要求，对原始数据进行处理，构建机器学习的有效样本集，以期提高最大发电能力计算模型的准确性。

1.1 特征选择

1.1.1 预测特征集

在进行基于数据挖掘的相关研究时，数据有效性是研究的基础。因此，为了提高模型系统的数据质量，必须找到真实数据集并对数据集进行预处理，以构建有效样本集。本文使用的数据取自宁夏某风电场的历史风力发电数据及相关气象特征数据。表1为预测关键特征集。

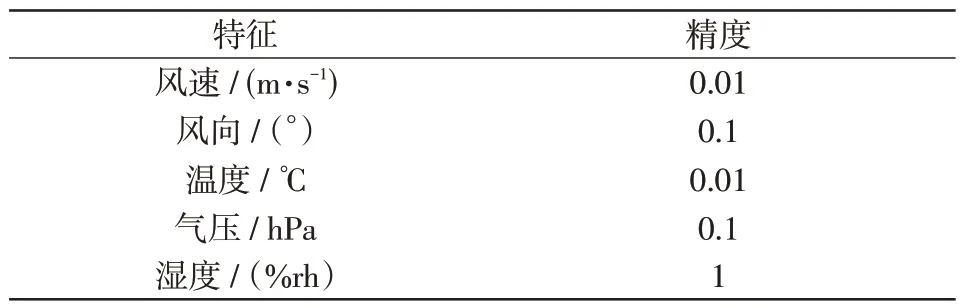
表1 预测关键特征集Tab.1 Key feature set for prediction

1.1.2 皮尔逊相关系数

在风电功率预测中，风电出力与功率预测关键特征之间具有相关性，但相关性的大小无法从数据集中直观看出，因而可以通过皮尔逊相关系数对模型输入特征进行筛选，去除掉相关性较弱的特征变量，保留两个强相关的特征变量作为模型输入，提高最大发电能力计算模型的训练速度与精度。变量X、Y的皮尔逊相关系数ρX,Y的计算公式为

式中：cov(X,Y)表示变量X、Y的协方差；σX、σY分别为变量X、Y的标准差。

本文所提模型旨在挖掘最大发电能力与关键特征变量之间的关系，因而在进行数据处理时可以在剔除零功率点后再对皮尔逊相关性进行统计计算。表2为数据集中6月历史数据的相关系数计算结果。可见，相较于其他特征，相关性最强的两个关键特征变量是风速和风向，因此选择风速和风向模型作为输入特征变量。

表2 皮尔逊相关系数结果分析Tab.2 Analysis of result of Pearson correlation coefficient

1.2 数据预处理

1.2.1 最大化处理

最大化处理是针对最大发电能力评估要求提出的，具有筛选有效数据点的功能，所以本文提出运用多项式曲面拟合迭代的方法筛选最大的风电出力点，以便构建后续机器学习的有效数据集。在经过特征选择后，将风向和风速作为输入特征变量，绘制风速-风向-出力的三维散点图。为了控制除风速、风向外的因素大致保持相同，可以将不同月份的数据分别进行处理，减小其他因素对最终预测结果的影响，实现简化控制变量的目的。

在获取三维散点图后，类比二维平面散点图构建上包络线的最大化处理方式，运用多项式平面拟合的思想，对三维散点图构建上包络面，构建的第1次曲面拟合示意如图1所示。

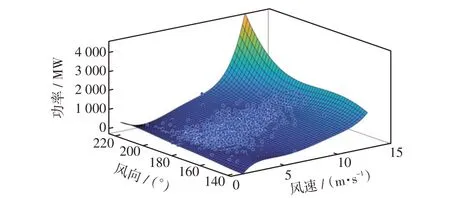
图1 第1 次曲面拟合示意Fig.1 Schematic of first-time surface fitting

采用线性回归对三维散点图构建拟合曲面，并对散点进行多项式曲面拟合，把所构造的曲面上部的散点筛选出来构成集合，将此集合中的散点重复上述操作，多次迭代使最终集合内的散点构建的曲面逼近逐于原始散点图的最佳上包络面。具体步骤如下。

步骤1分别以风速、风向、历史风电场出力为x轴、y轴、z轴，构建三维散点图，将原始数据组记为集合C0，在三维散点图中绘制出来。

步骤2运用多项式拟合曲面的思想方法，构造曲面拟合函数z=f(i)(x,y)，即

式中：i为迭代次数，i=0,1,2,…；pml为变量xm、yl的回归系数，m、l分别为x、y的幂指数，并定义利用原始数据进行初次拟合曲面时为第0次迭代。

步骤3在进行第i-1 次迭代时，设散点k为=(xk,yk,zk)(i-1)。若zk-f（i）(xk,yk)>0，则表示散点ck在曲面z=f（i-1）(x,y)的上部，筛选出满足上述条件的散点构成集合Ci，对此集合内的散点进行第i次迭代可得集合Ci+1。

步骤4若迭代满足card(Ci)-card(Ci+1)<β∙card(C0)，则迭代终止，取集合Ci中的元素作为有效样本点。其中，card()表示集合内元素的个数；β为迭代终止系数，β∈[0.05,0.10]。

1.2.2 归一化处理

数据的预处理环节除利用上包络面方法初步选出最大数据后，还需要对筛选出的有效数据进行归一化处理，以便最终作为有效样本集的一部分。对风电最大发电能力进行预测计算时，风速多数处于0～20 m/s，风向处于0°～360°，两者取值差异很大。对风速和风向归一化处理，有利于加快机器学习训练收敛速度，提高预测精度和建模效率。

1）风速归一化

在所提的风电最大发电能力计算模型中，可以类比传统风电功率预测，对风速进行归一化。风速归一化公式为

式中：vg为归一化后的风速；vt为天气预报系统预测的风速；vmax为气象观测的历史实际最大风速。

2）风向归一化

风向归一化之前，应设置好参考坐标轴，本文算例以正东方向为x轴正方向，正北方向为y轴正方向。风向的正弦值sinθ在(0°,180°)范围内取值为正，在(180°,360°)范围内取值为负；风向的余弦值cosθ在(0°,90°)和(270°,360°)范围内取值为正，在(90°,270°)范围内取值为负。因此，所有风向都可以利用正弦值和余弦值组合区分。

1.3 有效样本集的构建

有效样本集是指原始数据集在经过特征工程数据处理后，筛选出的可作为机器学习算法样本的数据集。风速和风向归一化后，可以得到风速归一化值、风向正弦值和余弦值3 个变量。将上述3 个变量作为机器学习模型样本集的输入变量，输出变量为风电场历史实时出力，因经过上包络面统计分析处理，样本集的输出变量在理论上是相同条件上的最大值。在进行机器学习时，需要将样本集按照给定比例随机划分成训练集和测试集，以便对模型的预测效果进行检验，具体操作示例详见第3.2节。

2 最大发电能力计算模型构建

2.1 算法选择

本文计算模型使用的学习算法属于SVM 的分支。SVM 是一种在统计分析基础上发展起来的学习算法，可以避免陷入局部最优的问题。SVM的主要功能有分类和回归，在样本数目较少的情况下明显优于其他机器学习算法[16]。新能源最大发电能力计算所用的机器学习样本集是从大量原始数据中筛选出5%～10%后形成的有效样本集，其样本数目较少，因此本文模型选用SVM进行学习。

采用SVM 训练样本数据，并以BP 神经网络作为对比，随机选取有效样本集的部分样本作为训练集进行训练学习，并将有效样本集的剩余样本作为测试集对所构建的学习模型性能进行分析。

本文模型的训练方法采用最小二乘回归算法，该算法可将机器学习复杂的“黑箱”计算转化为线性方程组的求解问题。设样本训练集合Traini={(x1,y1),(x2,y2),…,(xn,yn)} ，其中x∈R3，y∈R ，x=(vg,sinθ,cosθ)T，n为训练集中数据组数，在本文算例中n取100。基于上述样本的最小二乘SVM模型可表示为

式中：ϕ(xi)为xi的映射函数；G为自设定参数；J为损失函数；w为回归参数；b为常量回归参数；ei为残差。可见，式（4）所描述的SVM 回归问题就是计及ei情况下找寻最优的回归参数w、b使损失函数J最小化。。

式（4）的拉格朗日函数为

式中，αi为拉格朗日乘子。

对式（5）求极值可得

将式（5）和式（6）联立计算可得

在进行SVM 学习前，需要选定核函数。SVM的核函数可以是任何半正定函数，本文采用径向基核函数，又称作高斯函数。定义核函数k(xi∙xj)=ϕ(xi)∙ϕ(xj)，则可将上述问题的求解转化为线性方程组的求解，即

对式（8）求解可以求得回归系数αi和b。给定测试集Testi中序号为t的1组数据，则可以在已知输入变量xt的情况下，利用模型计算出预测值(xt)为

2.2 评价指标

本文选用的模型评价指标有相关系数和均方根误差。其中，相关系数越接近于1，均方根误差越小，模型性能越好，预测精度越高[17]。

1）相关系数

相关系数r能够反映预测最大发电功率和三维散点图上包络面实测最大发电功率波动趋势的相关程度。r可表示为

式中：PM,i为样本测试集序号为i的风电场实测功率；PP,i为样本测试集序号为i的风电场预测功率；N为测试集样本数目；为测试集样本实测功率的平均值；为测试集样本预测功率的平均值。

2）均方根误差

均方根误差Ermse是衡量机器学习优越性最常用的误差评价指标。Ermse可表示为

式中，si为样本测试集序号为i的风电场开机容量。

2.3 模型构建

本文模型主要包括特征工程阶段、预测计算阶段和评价阶段3个阶段，模型结构如图2所示。

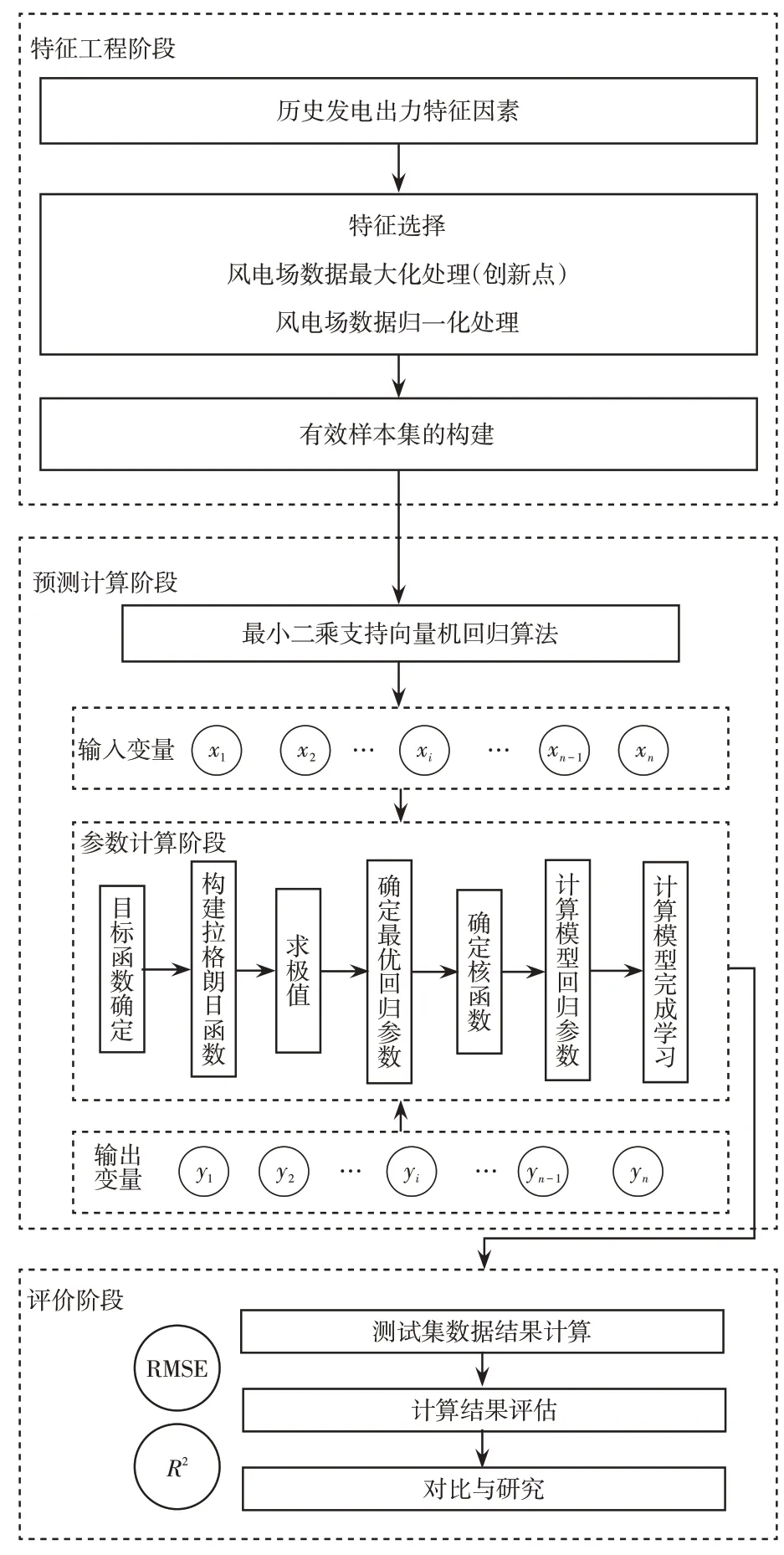
图2 模型结构Fig.2 Model structure

3 算例分析

3.1 风电场数据集最大化处理

以我国某风电场2021 年6 月部分数据信息为例进行分析，选取2 138个时刻点，在每个时刻点下该风电场区域风速、风向和实际输出功率3个信息数据均可获得。以风速为x轴、风向为y轴、风电机组历史实时出力为z轴构建立体直角坐标系，以获取的数据集为依据，绘制风力发电机组风速-风向-出力三维散点图，如图3 所示。同时，将原始数据集中散点以ci=(xi,yi,zi)的形式构成集合C0。

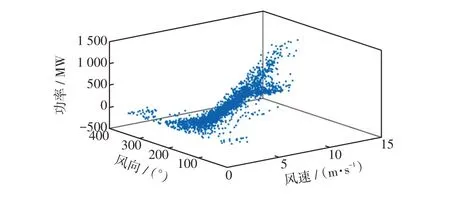
图3 风电机组风速-风向-出力三维散点示意Fig.3 Three-dimensional scatter diagram of wind speedwind direction-output from wind turbine

构建多项式拟合曲面的目标是找到上包络面，但仅进行1 次多项式拟合无法找到上包络面。因此，为了找到目标样本点，运用迭代思想，多次构建多项式拟合曲面。

第1次曲面拟合曲面如图4（a）所示，从集合C0选出满足zi-f(0)(xi,yi)>0 的散点构成集合C1，经过仿真计算，集合C1内有散点681个。然后利用集合C1中的散点进行第2次曲面拟合，从集合C1选出满足zi-f(1)(xi,yi)>0 的散点构成集合C2，经过仿真计算，集合C2内有散点278 个，拟合曲面如图4（b）所示。重复上述操作，再次迭代，第3次和第4次曲面拟合如图4（c）和（d）所示。迭代终止条件是两次迭代目标集合元素数目差第1 次小于原始样本点数目的5%，取本次进行迭代的元素作为有效样本点。经对集合散点数进行计算可得，card(C3)-card(C4)=127-57=70<107，即第1 次满足迭代终止条件，并取集合C3为有效数据集。

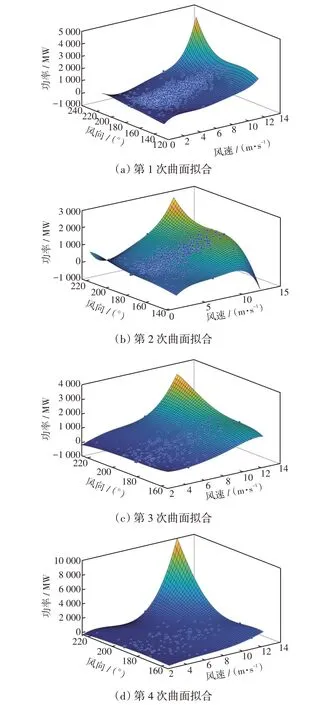
图4 上包络面构建过程Fig.4 Construction process of upper envelope surface

3.2 风电场最大发电能力SVM 算法预测结果

在进行机器学习时，需要将样本集按照给定比例随机划分成训练集和测试集，以便对模型效果进行检验。针对本文算例，将集合C3中归一化后的风速、风向正弦值和余弦值作为输入，相应的风电场历史实时出力作为输出。在127个数据组中，随机选取100个数据组作为训练集，剩余的27个数据组作为测试集。

第i次仿真实验的有效样本集随机分配过程中，设训练集合为Traini={(x1,y1),(x2,y2),…,(x100,y100)}；测试集合Testi={(x101,y101),(x102,y102),…,(x127,y127)};x∈R3,y∈R。

根据第1 次仿真实验训练集Train1内的数据集，利用SVM 算法对模型进行训练，可得到训练集Train1的训练情况如图5 所示。然后，利用训练后的模型对测试集Test1进行测试，可得测试集Test1的训练结果如图6所示。

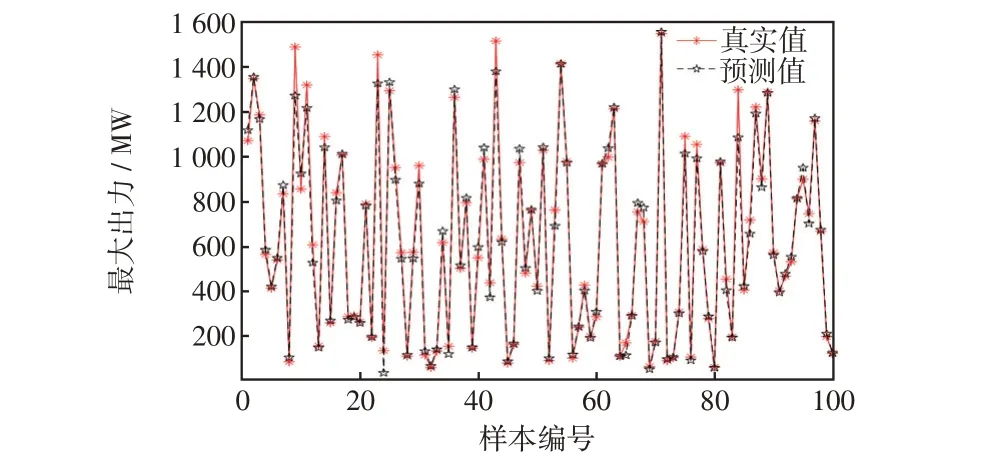
图5 训练集Train1预测结果对比（SVM）Fig.5 Comparison of prediction results based on training set Train1（SVM）

图6 测试集Test1预测结果对比（SVM）Fig.6 Comparison of prediction results based on test set Test1（SVM）

为了能够更好地比较两种机器学习方法的性能，可以将BP 神经网络、SVM 预测结果同时与期望值（即真实值）作对比，结果如图7所示。可以看出，虽然样本序号为25 的SVM 预测值比BP 神经网络预测值较真实值偏差更大，但总体来说偏差并不大；对于样本序号4、21、23、24，BP 神经网络预测值误差太大，不能起到最大发电能力计算的效果，预测准确性较差；样本序号为1、5、6、8、9、11、13、14、15、16、18、26 的SVM 预测值均优于BP 网络预测值。在剩下的测试样本中，两者预测效果大致相同。

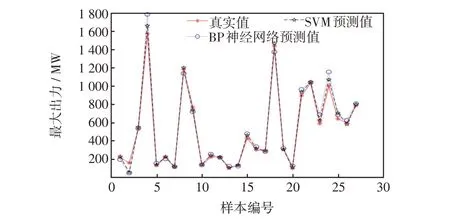
图7 两种算法测试集结果对比Fig.7 Comparison of results based on test set between two algorithms

为了对本文模型进行评价，这里进行3 次仿真，即Traini和Testi中i=1,2,3，取3次仿真结果的平均值来进行衡量。两种机器学习方法的评价指标如表3所示。

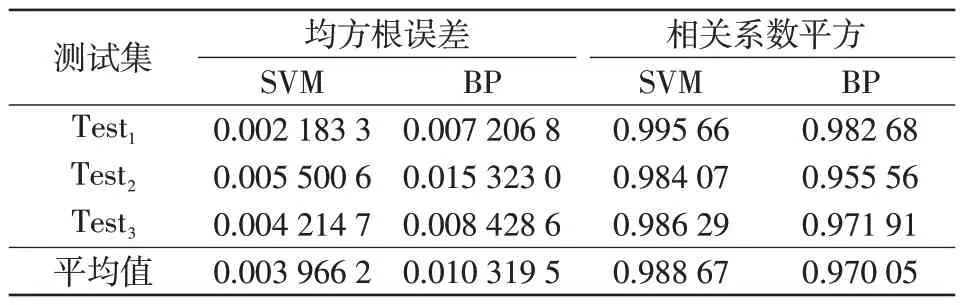
表3 仿真结果记录Tab.3 Record of simulation result

由表3 可知，对于均方根误差，采用SVM 构建模型的平均误差不到0.4%，而采用BP 神经网络的平均误差超过1%，即SVM比BP神经网络的均方根误差更小；对于相关系数平方，采用SVM构建模型，3次仿真结果均在0.98以上，而BP神经网络则明显低于0.98，即采用SVM构建模型的相关系数更接近1，充分体现了采用SVM 构建模型相关性分析的有效性。