基于贝叶斯与深度学习结合的变压器故障诊断

2023-10-07马天龙李宁瑞赵立宇

电力系统及其自动化学报 2023年9期

霍浩，马天龙，李宁瑞，康超，赵立宇，孙伟

（国网甘肃省电力公司超高压公司，兰州 730070）

电力变压器在电网中承担着至关重要的作用[1]。目前，绝大多数变压器为油浸式变压器，当变压器内部出现故障时，绝缘油将受热分解产生H2、CH4、C2H6、C2H4和C2H2等气体[2]。因此，溶解气体分析DGA（dissolved gas analysis）是油浸式变压器运行状态分析与故障诊断的重要手段[3]。依据DGA结果准确判断变压器状态是电网安全稳定运行的重要保障[4]。

传统的故障诊断方法包括关键气体法、Rogers比值法、Dornenburg比值法、IEC比值法、Duval三角形法等[5]。然而，这些方法存在过度依赖主观知识、边界固定等问题，故障诊断准确率较低。近年来，人工智能方法凭借其强大的非线性表示能力，为变压器故障诊断提供了新思路[6]。目前应用于变压器故障诊断的人工智能方法主要分为支持向量机SVM（support vector machine）与神经网络两大类。

SVM方法根据超平面切割的思想，基于核函数实现非线性分类，已在变压器故障辨识领域取得了较好的效果[7]。SVM方法的辨识准确度与超参数高度相关，因此学者们提出了多种方法进行SVM超参数寻优。例如麻雀搜索[8]和磷虾群[9]等多种启发式智能算法均被用于搜索SVM 的惩罚因子、核参数、集成算法的分类器权重等。同时，SVM方法对输入特征类型的选择较为敏感，为进一步提高SVM模型的诊断精度，有学者提出了基于随机森林的多特征优选方法[10]，从气体成分百分比、气体比值等多特征中进行寻优。考虑到数据集可能存在各类样本数量不平衡的问题，文献[11]提出了基于托梅克链接移除核自适应样本合成的方法，对原始数据进行去噪处理，提高了故障诊断精度。利用Smote-Borderline合成样本也可获得完备均衡的数据集[12]。然而，受限于自身特性，SVM 方法实现故障诊断时的划分依据相对固定，且仅给出变压器是否故障的单一结果。当变压器处于边界状态或用于训练与预测的数据存在误差时，SVM方法可能存在误判或漏判的问题。

神经网络方法具有强大的表示能力，能够从复杂特征中的输入与输出学习非线性映射关系，对输入特征的选择要求低于SVM 方法。基于混合核极限学习机的变压器故障诊断方法[13]将灰狼算法与差分进化算法结合进行参数寻优，防止极限学习机陷入局部最小。基于图卷积网络的故障诊断方法[14]则利用邻接矩阵的形式度量不同样本间的差异，提高了网络对输入数据的特征提取能力。然而，神经网络方法需要大量数据进行训练，而变压器DGA的频率多为每年1、2次，累积的历史数据量有限，且大多为正常状态数据，导致网络容易陷入过拟合。针对该问题，基于深度置信网络的变压器故障辨识[15]采用分级预训练方法，可在预设大样本数据集上预训练并在实测的小样本数据集上进行参数微调。文献[16]基于数据特征增强方法扩充了输入数据的特征标签，使得输入数据在高维特征空间的相对距离增加，抑制网络过拟合。然而，上述方法无法对变压器状态的不确定性建模，难以定量评价边界状态变压器的健康状况。同时，现有神经网络方法对预测样本的准确度要求较高，当数据存在误差时，该误差可能经神经网络的复杂前向传播放大，影响故障识别的准确度。

针对上述问题，本文提出基于一种贝叶斯与深度学习结合的变压器故障诊断方法。首先将贝叶斯方法引入深度神经网络，构建基于概率分布权重单元的贝叶斯神经网络；其次，在保留深度学习强大非线性特征映射能力的同时，基于贝叶斯方法推理变压器状态数据在高维空间中的分布，抑制过拟合；然后，基于蒙特卡罗法拟合变压器故障概率，引入安全阈值量化变压器的健康情况，提高对边界状态变压器的诊断正确率；最后，对传统反向传播BP（back propagation）神经网络法、粒子群优化、支持向量机法、残差收缩网络法及本文方法进行对比，并对结果进行可视化，直观展示故障识别结果，构造含高斯分布误差的数据集，验证所提方法对样本误差的适应能力。

1 贝叶斯方法与深度学习的结合

传统深度学习采用多层神经网络前向传播的方式模拟人类神经元，并训练网络实现复杂非线性映射功能，其中全连接层的前向传播表达式为

式中：yi为本层第i个单元的输出；J为上一层的总单元数；ωj为上层第j个单元到本单元的权重；xj为上层第j个单元输入到本单元的输入；bj为上层第j个单元到本单元的偏置；f( )为非线性激活函数，通常为ReLU或Sigmoid函数。

深度神经网络需在训练中优化权重与偏置参数，使得输出逼近真实值。因此，可将输入集合为X、输出集合为Y、权重集合为W的神经网络视为条件分布p(Y|X,W)。在分类问题中，该分布对应各类的概率；在回归问题中，该分布的均值对应预测结果。神经网络的权重训练可视作求解以下最大似然估计：

式中：W*为训练完成后的单元权重；D为用于训练的数据集；p(D|W)为数据集D在权重集合W下的映射概率分布。

在分类问题中，将Logistic 函数代入条件分布则可得到交叉熵；在回归问题中，将高斯分布代入条件分布则可得到均方误差。一般采用反向传播法求解该问题的极值点，从而确定网络权重。

为提高神经网络对不确定性数据的学习能力，将贝叶斯方法与深度学习结合，假设权重服从概率分布，构建贝叶斯神经网络模型。贝叶斯神经网络的典型单元结构如图1所示。

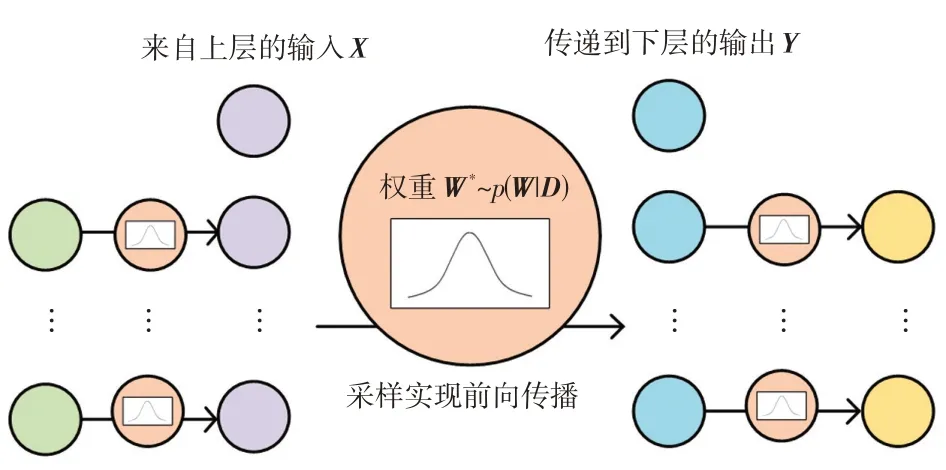
图1 贝叶斯神经网络单元结构Fig.1 Structure of Bayesian neural network unit

贝叶斯神经网络的条件分布模型可表示为

式中，Ep(W|D)(p(Y|X,W) )表示概率分布p(W) 在p(Y|X,W)中的数学期望。

贝叶斯神经网络的训练目标是根据输入数据集D，确定权重W的最佳后验分布p(W|D)，从而使得式（2）成立。

贝叶斯神经网络兼顾了深度学习与贝叶斯方法的优点。一方面，深度学习具有强大的表示能力，可在监督训练中学习绝缘油溶解气体与变压器状态间的非线性映射关系，无需通过主观构建判据，克服了传统比值方法过于依赖人为经验的问题；另一方面，贝叶斯方法为神经网络提供了量化不确定性的能力，能够给出变压器状态的完整概率信息，提高故障诊断的准确性，且贝叶斯神经网络的鲁棒性良好，能够适应样本数据的误差。此外，由于权重服从概率分布，网络依分布抽样实现前向传播，每次前向传播的结果均不相同。因此，贝叶斯神经网络也可视为无数个确定性神经网络的集成[17]，具有优秀的正则化效果，显著降低了神经网络的过拟合程度。与其他集成神经网络不同的是，贝叶斯神经网络在每轮训练中更新权重后验分布，实现了所有子神经网络的同时更新，比其他集成神经网络的计算用时更少。

2 变压器故障诊断模型

2.1 原始数据预处理

选取DGA 结果中H2、CH4、C2H6、C2H4和C2H2作为绝缘油中的关键气体[18]，并作为贝叶斯神经网络的输入特征。由于各气体成分占比在数量级上差异较大，直接作为输入特征将导致数据样本空间过于稀疏，影响训练效果，因此将数据集依特征进行标准化，标准化公式为

式中：X0为原数据集；Xref为标准化后的输入数据集；Xmean为输入X0的各特征分量均值；Xstd为输入X0的各特征分量标准差。

变压器故障诊断是一个典型的多分类问题。考虑油浸式变压器的6 种典型故障[19]，采用one-hot编码将故障状态转化为易于训练的标签，其故障特性及对应的输出标签如表1所示，可根据输出单元的结果确定变压器的具体故障类型。

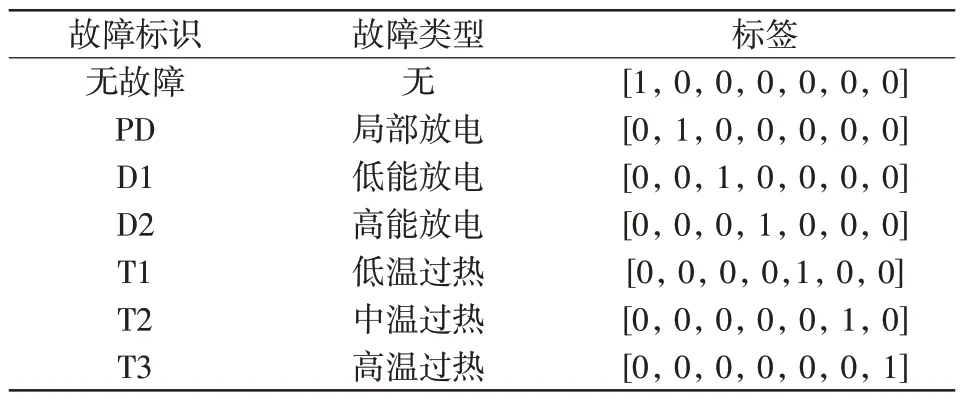
表1 变压器故障标签Tab.1 Labels of transformer fault

2.2 超参数设置

神经网络的超参数是影响训练效果的重要因素，包括设置网络单元参数与确定梯度下降算法。在本文构建的贝叶斯神经网络模型中，输入层为5个单元，对应标准化后的5种DGA结果；输出层为7个单元，对应7 种故障诊断结果。同时，由于数据量较少，为防止过拟合，不宜使用层数过深或单元数过多的网络，选择隐藏层为2 层概率全连接层，单元数分别为16和8。采用Adam算法实现梯度下降，Adam算法引入了偏置修正因子以抑制训练初期二阶矩偏置过高的现象，并采用自适应参数学习率，对初始学习率、训练轮次等参数进行选择，鲁棒性更好[20]。采用早停策略决定训练总轮次，设置连续3轮内网络损失值的变化率不超过1%时停止训练。

2.3 网络训练

式中：θ*为训练完成后的分布q参数；divergence(p,q)表示衡量两个分布间距离的函数。

引入KL散度DKL来衡量两个分布的差异，DKL可以表示为

定义证据下界L为

这样求解KL散度最小等价于L(D,θ)取得最大值。将式（7）依KL散度的定义展开可得

式中，p(W)为权重的先验概率分布。

式（8）中等号右侧第1 项为贝叶斯神经网络模型的后验对数概率，可在每轮训练中通过对总样本的小批量抽样蒙特卡罗近似条件似然求解；第2项为权重分布p(W)的先验概率分布，一般假设其为标准高斯分布或伯努利分布；第3 项为所构建q(W|θ)的概率分布，一般采用均值场（mean-field）方法构建，假设各单元权重服从均值为0、相互独立的高斯分布，则可通过对每个分布求对数后取平均值计算期望，训练时仅需更新分布q的方差即可。对式（8）可采用梯度下降法求得L(D,θ)的极值，第m个权重分布的方差σm的更新公式为

式中，g( )为迭代因子函数，由具体的梯度下降算法给定。

2.4 故障诊断

网络训练完成后，基于蒙特卡罗法将待诊断的数据多次输入贝叶斯神经网络进行前向传播，根据输出在不同标签上的分布拟合变压器故障概率。

引入安全阈值的概念，认为故障概率大于安全阈值的变压器处于故障状态。在实际工程中有两种方法确定安全阈值：①根据运行检修人员经验将安全阈值设定为检修计划最大容许值，以保证电网的安全性；②在历史数据集中随机划出部分数据为不参与训练的测试集，使用其余数据训练故障诊断模型，并在测试集上进行故障诊断，选择故障诊断效果最好的安全阈值，兼顾电网的安全性与经济性。此外，还可设置多级不同的安全阈值，根据变压器故障概率所处的安全阈值区间，决定是否对变压器采取检修或加强观察等措施。

实际工程中，由于DGA 结果存在一定误差，传统方法对边界状态变压器的故障诊断准确率可能进一步降低，本文方法给出的变压器故障概率也会出现小范围波动。然而，本文方法可以基于搜索最佳安全阈值的方法，获取更合理的量化评判标准，降低故障概率波动的影响，提高故障诊断的准确率，从而提高故障诊断方法对输入数据误差的鲁棒性。

综上所述，基于贝叶斯神经网络的变压器故障诊断流程如图2所示。

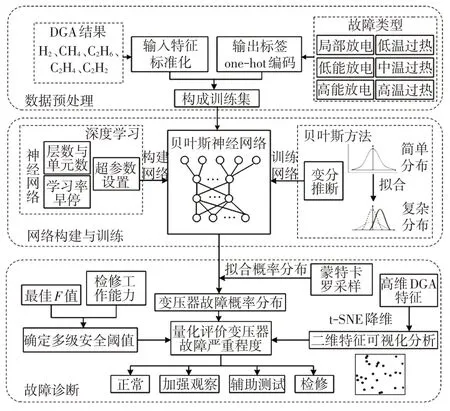
图2 基于贝叶斯神经网络的变压器故障诊断流程Fig.2 Process of transformer fault diagnosis based on Bayesian neural network

3 算例分析

3.1 算例介绍

本文基于Python 平台与TensorFlow 后端实现贝叶斯神经网络的构建与训练。计算设备的CPU为英特尔酷睿i7-9700k，计算卡为NVIDIA-GTX2060 12G。算例的数据集由某市变压器近4年的实测数据与IEC TC10 数据库中数据样本构成，共计2 300条样本数据，其中各类故障数据共942 条，正常数据共1 358条。

3.2 基于F 值评价的故障诊断结果分析

随机将数据集中80%的数据划分为训练集，其余20%为验证集，输入所构建的贝叶斯神经网络模型进行训练。经数据预处理后，将1 840 条训练数据以随机顺序进行训练，经过18轮迭代后，满足提前终止条件，即网络训练完成。基于贝叶斯神经网络对所有数据进行1 000 次蒙特卡罗模拟，拟合其故障概率分布。

传统方法采用准确率作为单一的故障诊断结果时，无法有效区分误判与漏判，因此本文引入查准率P、查全率R与F值作为故障诊断综合准确率，可分别表示为

式中：Nfp为实际故障变压器被诊断为故障状态的台数；Nfa为被诊断为故障状态变压器的总台数；Nf为实际故障变压器的总台数；F为查准率P与查全率R的综合评价指标；β为评分系数，若系数β高则查准率更重要，若系数β低则查全率更重要，β=1时两者重要程度相同。

查全率是故障状态变压器被成功诊断的比例，若查全率较低，则可能导致漏判，使得故障进一步恶化，影响电网稳定运行。查准率是被诊断为故障变压器中明确为故障状态的比例，若查准率较低，则可能导致故障误报，为运行检修带来额外工作量，影响电网经济运行。考虑故障漏判的影响一般大于故障误报，设置F值的评分系数为0.5。此外，本文方法给出的故障诊断结果为蒙特卡罗法拟合的故障概率，当安全阈值改变时，故障诊断结果也将随之变化。仅考虑设备的故障或正常两种状态时，查全率、查准率及F值评分随安全阈值变化情况如图3所示。

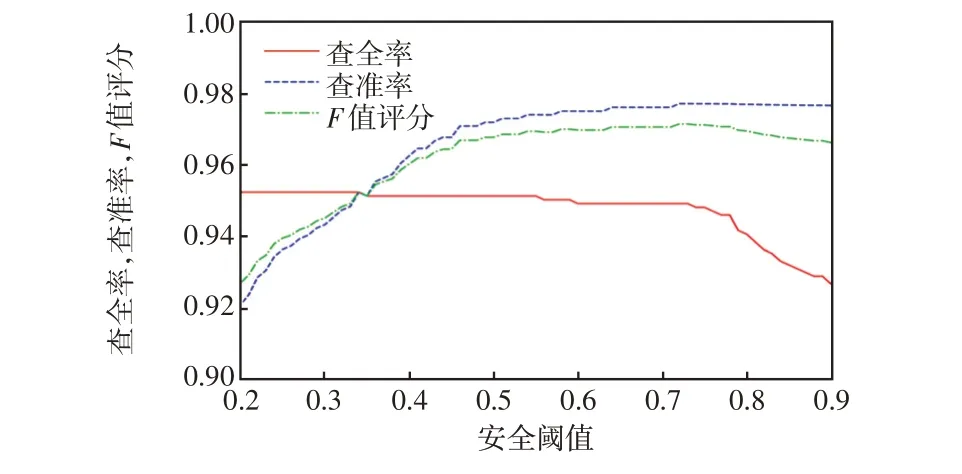
图3 不同安全阈值下的故障诊断F 值评分Fig.3 F-score of fault diagnosis under different safety thresholds

进一步选取传统BP神经网络法（方法1）、粒子群优化参数的支持向量机法[21]（方法2）及残差收缩网络法[16]（方法3）进行对比，本文方法对不同类型故障的诊断结果F值评分与其他方法的故障诊断结果对比如表2 所示。各方法在所有样本上的总体查全率、总体查准率与总体F值评分如表3 所示。由图3 可知，本文方法取得最高F值评分的安全阈值为0.73。

从表2 和表3 可以看出，当本文方法的安全阈值变低（变严格）时，查全率明显升高而查准率降低。当安全阈值设定过高时，故障诊断对实际故障的查全率有限；当安全阈值设定过低时，故障诊断将出现大量误报。当安全阈值设定为0.73时，本文方法在各类故障上的F值评分及总体评分均高于传统方法，验证了本文方法的有效性。

从上述仿真结果可以看出，本文方法的最佳F值评分优于其他3 种传统方法。本文方法一方面利用深度学习的高度非线性映射能力，准确建立了DGA特征与故障类型间的映射关系；另一方面利用贝叶斯方法将传统深度学习改进为概率映射模型，不仅能够判断出变压器是否处于故障状态，也可利用故障概率值定量评价变压器的健康程度。例如在实际工程中，可设计多级不同的安全阈值，依据变压器故障概率所处的区间，从而对不同健康程度的变压器分别采取停运检修、开展辅助检测或缩短检测间隔等措施。同时，在安排检修计划时，也可根据不同变压器的故障概率值，合理安排变压器的检修顺序。

3.3 边界状态变压器故障诊断可视化分析

为直观展示本文方法对故障状态边界变压器的故障诊断效果，对变压器的特征及状态进行可视化，利用t分布邻域嵌入t-SNE（t-distributed stochastic neighbor embedding）方法将数据集内各条数据的五维气体成分特征降至二维。t-SNE是一种常用的高维数据可视化方法，其假设高维空间数据服从高斯分布，低维空间数据服从t分布，基于梯度下降方法最小化数据点在高低维空间下的KL 散度，在保持数据在高维空间相对距离的前提下映射至低维空间[22]。以变压器降维后的二维特征作为横纵坐标，以变压器故障情况作为数据点的特征，可对实际故障的分布情况可视化。考虑到图像的清晰度，选取部分距离边界状态较近的变压器作图，结果如图4所示。可以看出，正常设备数据与故障设备数据呈现出明显的区分态势，然而在方框所示的状态边界，变压器状态区分不明显。采用传统方法对该类数据进行故障诊断时，容易出现误判或漏判。

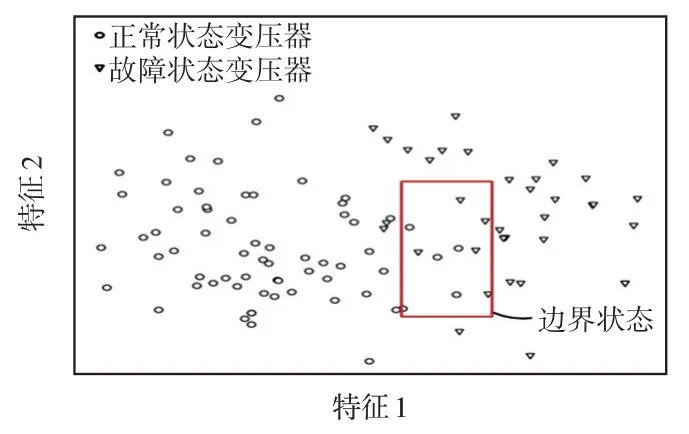
图4 变压器故障状态的可视化Fig.4 Visualization of transformer fault state

基于t-SNE方法做出基于粒子群优化参数的支持向量机法的故障诊断结果的可视化如图5 所示。本文方法故障诊断结果的可视化如图6所示。

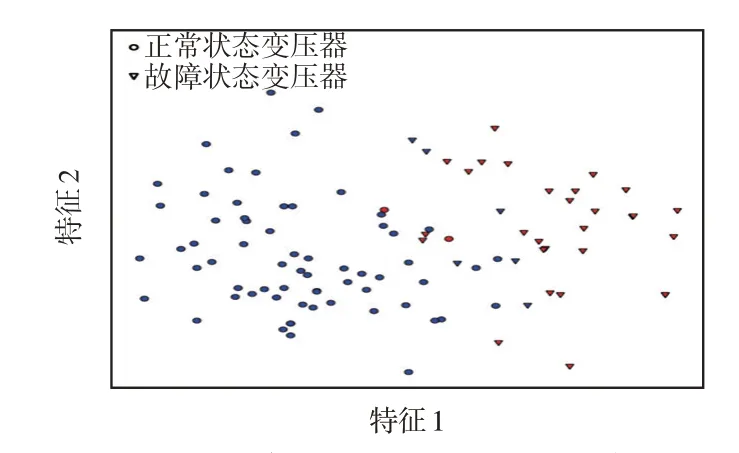
图5 基于粒子群优化参数支持向量机法的故障诊断的可视化Fig.5 Visualization of fault diagnosis based on particle swarm optimization parameters SVM

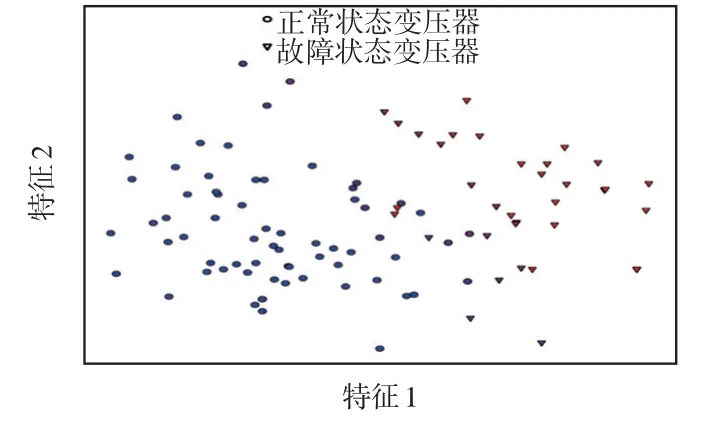
图6 基于贝叶斯神经网络的故障诊断结果的可视化Fig.6 Visualization of fault diagnosis result based on Bayesian neural network

从图5 可以看出，传统方法的变压器故障诊断技术基于固定的划分标准，对边界状态变压器给出故障或正常的诊断结果时易出现误判或漏判。而本文方法既能够准确辨识距离边界较远的变压器状态，又能够给出边界状态变压器的故障概率，并定量描述变压器的健康情况，提示决策者对该类变压器采取相应措施。

3.4 考虑数据误差的故障诊断分析

在实际工程中，变压器绝缘油采样分析过程可能存在故障气体的扩散程度不均匀、振荡脱气不充分、漏气等问题，数据将出现误差，导致位于边界状态的变压器出现误判。国标GB/T 17623—2017 在绝缘油中溶解气体组分含量的气相色谱测定法中针对检测精密度有以下规定：测定差应小于平均值的10%。因此，为验证本文方法对样本误差的适应程度，在测试集内所有样本数据中引入服从高斯分布的误差，误差均值为0，方差为该特征值的5%。基于新测试集，各方法的查全率、查准率及F值评分如表4所示。测试集上的最高F值评分在安全阈值为0.59时取得。

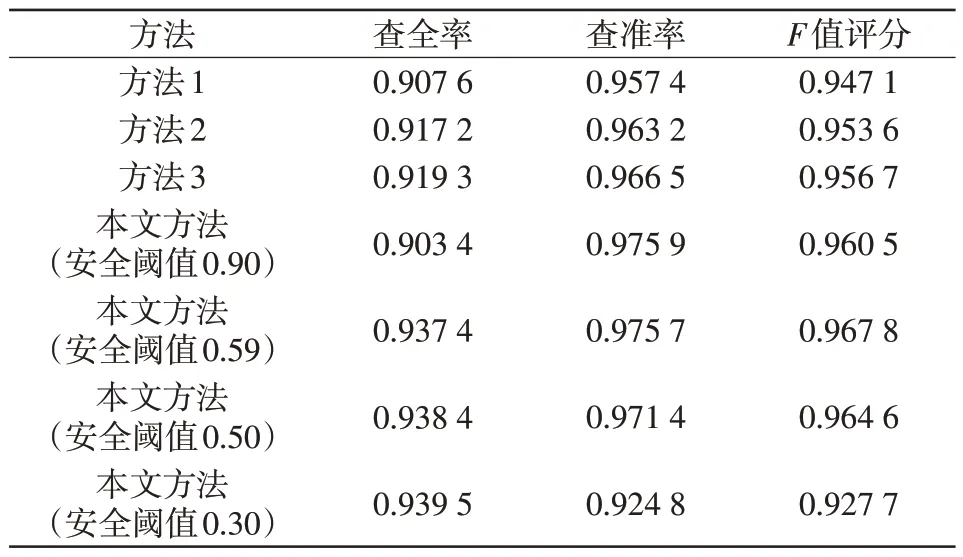
表4 引入误差后的总体评分对比Tab.4 Comparison of overall svore with error in data

引入误差后，传统方法与本文方法的故障诊断结果均受到一定影响。传统故障诊断方法的F值评分均下降了0.01 左右，诊断查全率降低2%左右。本文所法在不同安全阈值下的F值评分也出现了波动，安全阈值为0.59 时取得最佳F值评分，且仅比误差引入前的最佳F值降低约0.003 5，诊断查全率降低约1.2%。可见，本文方法所受影响远小于传统方法。进一步分析其原因，在样本数据出现误差时，数据点会因该误差而改变自身在高维空间的位置。对于边界状态变压器，小范围的空间位置改变便可能导致其跨越传统方法的分类边界，进而导致故障诊断的准确率降低。而在本文方法中，数据点在高维空间中的移动将反映为变压器故障概率的改变，其所代表的变压器状态仅在不同的安全阈值区间内变动，根据不同安全阈值下的设备数量分布重新选择恰当的安全阈值后，本文方法仍可获得较高的F值评分。上述分析表明，本文方法的变压器故障状态量化评判标准更为合理，能够降低变压器故障概率波动的影响，提高故障诊断方法对输入数据误差的鲁棒性。