基于多特征融合与优化支持向量机的小电流接地故障区段定位方法
2023-10-07杜政奇王敬华张新慧李晨朝王洪庆
杜政奇,王敬华,张新慧,李晨朝,王洪庆,张 莹
(1.山东理工大学电气与电子工程学院,淄博 255049;2.山东科汇电力自动化股份有限公司,淄博 255087)
随着电力系统规模扩大,各类型故障频发,故障后需快速检测出故障位置,隔离故障区段进而恢复供电,但谐振接地系统发生故障时特征信号微弱,给定位造成困难[1]。现有数据表明,电网80%以上的故障均发生在配网侧,因配电网作为与用户直接连接的环节,研究配电网故障定位方法对提高配电网供电可靠性具有重要意义。
现有故障定位技术多以单一特征量为依据来进行故障定位。文献[2]采用故障点上下游主谐振分量振荡频率的差异来实现故障区段定位,但在故障点上下游线路长度一致且高阻接地情况下,故障点上下游零序电流振荡频率相似且接近工频,容易造成误判。文献[3]利用广义S 变换得到暂态零序电流时频矩阵,以相对熵来衡量故障点上下游的能量差异,对于自动化较低的系统无法满足同步采样的要求。文献[4-5]利用动态时间弯曲距离DTW(dynamic time warping)来描述故障区段两侧的暂态零序电流波形差异,一定程度上解决了采样不同步的问题,在低阻接地时也具有良好的效果,但在高阻接地时易受线路类型的影响,由于架空线路对地电容远小于电缆线路,在单相接地故障发生在架空线路区段内时会出现非故障区段稳态零序分量大于故障区段的情况,影响定位可靠性。文献[6]提取暂态零模电流并构造衰减速度判据,但在高阻接地情况下,暂态高频分量振荡频率接近工频,在一定情况下需要十几个工频周期才会衰减至0,截取的数据窗不易确定。
随着经验模态分解EMD(empirical model decomposition)、集合经验模态分解EEMD(ensemble empirical mode decomposition)、互补集合经验模态分解CEEMD(complementary ensemble empirical mode decomposition)等信号处理算法的发展,故障特征量的获取更加便捷,但一些算法本身存在一定缺陷,与理论计算的故障特征量存在偏差。文献[7]利用EMD自适应分解各出线零序电流,并有效解决了EMD算法本身模态混叠的缺陷,但需要选取故障特征明显的有效分量。文献[8-10]采用变分模态分解VMD(variational mode decomposition)算法分解暂态零序电流获得特征模态分量IMF(intrinsic mode function)时,分解层数K设置为3,但由于故障点下游暂态零序电流第3 个本征模态分量相较于其余高频信号能量较小,无法准确得到暂态零序电流信号的暂态高频分量。文献[11]采用边界延拓方法对局部均值分解LMD(local mean decomposition)进行改进,消除端点效应和模态混叠问题,并应用于暂态零序电流分解。同时,人工智能的发展为故障定位问题转化为机器学习中的分类问题提供了新思路。文献[12]将轻量级梯度提升机LightGBM 应用到故障区段定位中,但由于故障特征量的选取只适用于中性点不接地系统,在经消弧线圈接地系统中容易引起误判。文献[13]搭建了基于电压与数据之间相关性的支持向量机SVM(support vector machine)的故障定位模型,其分类结果准确率不仅与最优特征维数相关,还受SVM算法本身关键参数影响。此外,贝叶斯[14]、模糊聚类[15]等分类算法均已被广泛应用到配电网故障分析中。
传统故障定位方法多采用阈值整定的方法,故障定位准确度不高。为此,本文在小电流接地系统发生接地故障时,分析研究故障线路各区段暂态零序电流的特征,并在此基础上提出一种利用自适应VMD构造多种故障特征量和优化SVM融合特征的区段定位新方法。首先利用暂态过程主谐振能量最大原理对VMD 的分解层数K进行自适应优化,然后分解故障暂态零序电流得到1组IMF。从时域和频域两个方面分析暂态量蕴含的多种故障信息,构造了5种不同的故障特征量,将高维特征向量输入到改进鲸鱼优化算法IWOA(improved whale optimization algorithm)优化的故障定位SVM分类模型中进行训练,最后输出故障区段定位结果。所提方法将区段定位问题转化为分类问题,提高了故障定位的可靠性。
1 单相接地故障暂态特征分析
为了判定本文所选故障特征量在故障区段定位问题中的有效性,在忽略线路阻抗的前提下,图1给出了适用于分析健全线路和故障线路各区段暂态零序电流的分布特征。其中,S1为包含全部健全线路的等效故障检测点;S2、S3为故障点上游区段的相邻故障检测点;S4、S5为故障点下游区段的相邻故障检测点;iCs为流经全部健全线路的对地电容电流之和;iLp为流经消弧线圈的暂态电感电流;iCu1、iCu2为故障点到母线侧各区段内的对地电容电流;iCd1、iCd2为故障点到负荷侧各区段的对地电容电流。
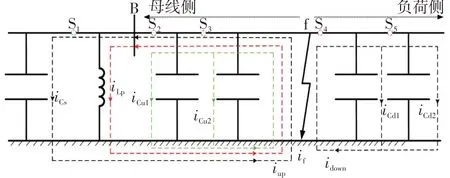
图1 故障零序电流分布Fig.1 Distribution of fault zero-sequence current
由图1 故障零序电流流向可知,流经故障点的暂态零序电流可表示为
式中:if为流经接地点的暂态零序电流;iup为流经故障点上游的暂态零序电流;idown为流经故障点下游的暂态零序电流。流经故障点上游和下游暂态零序电流表达式分别为
由图1 可知,故障点上游相邻检测点S2和S3零序电流之差为iCu1,故障点下游相邻检测点S4和S5零序电流之差iCd1。可见,故障线路上各检测点暂态零序电流的差异为故障区段定位提供了判定依据。
对于谐振接地系统,故障零序电流分量[15]可表示为
式中:ω0为工频频率;;δc为主谐振分量的衰减因子,δc=R2L,其中R和L分别为零模网络中等值电阻和电感;δL为衰减直流分量的时间常数,δL=RfLp,其中Lp为消弧线圈等值电感,Rf为故障点过渡电阻;ILm=Umω0Lp,ICm=Umω0C,其中Um为系统虚拟电压源幅值,C为零模网络中等值电容。
2 VMD 及最优参数选取
2.1 变分模态分解
当配电网发生单相接地故障时,故障线路上的零序电流会发生突变,由馈线终端采集的零序电流信号中存在类似于IMF 的调幅-调频信号。为了验证采用VMD[16]分析暂态零序电流信号的可行性,根据式(4)可构造1组仿真信号,即
式中:x1(t)为衰减直流分量;x2(t)为稳态工频分量;x3(t)为暂态主频分量。
由式(5)可知,该仿真信号主要包含0 Hz、50 Hz和500 Hz 这3 个频率成分。VMD 算法预先设置的参数主要有分解层数K、惩罚因子α、凸函数优化相关参数、中心频率初始化参数、中心频率更新时的相关参数。
采用VMD对信号x( )t进行分解,设置分解层数K=3,惩罚因子α=20 000,分解结果如图2所示。
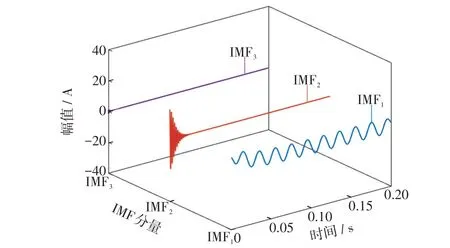
图2 仿真信号的VMD(K=3)Fig.2 VMD of simulation signal(K=3)
由图2 可知,当信号中存在衰减直流分量时,设置K= 3 并不能很好地分解仿真信号,x1(t)和x2(t)被分解到同一模态分量(IMF1)中且出现了虚假分量IMF3。为了准确分解暂态零序电流中的衰减直流分量,将IMF1经VMD二次分解,分解结果如图3所示。
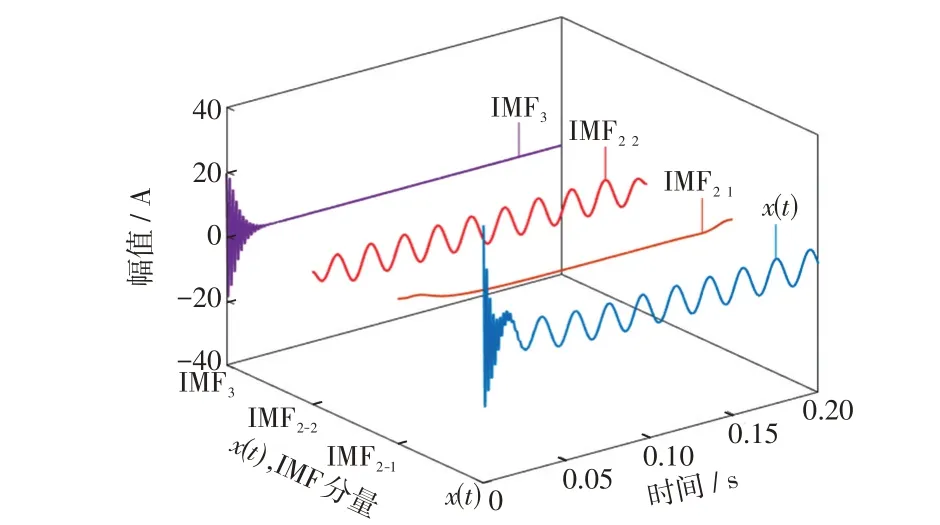
图3 原始信号及最终分解效果Fig.3 Original signal and final decomposition renderings
图3中,x(t)为原始信号;IMF2-1为二次分解得到的衰减直流分量;IMF2-2为二次分解得到的稳态工频分量;IMF3为暂态主频分量,与原始信号组成的分量一致。
2.2 最优模态参数选取
VMD算法中除分解层数和惩罚因子之外,其他参数对分解效果的影响并不明显,通常设置为经验值。分解层K对VMD 的分解效果影响较大,参数K选取合适是取得良好分解效果的关键,因此本文只讨论参数K的选取。
谐振接地系统发生单相接地故障时,其暂态过程包含了由模网络相互作用引起的多个串并联谐振过程。图4 为一次故障中暂态零序电流在高频段的幅频特性。
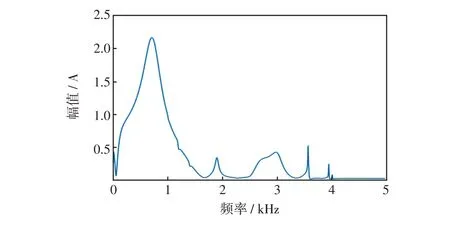
图4 暂态零序电流高频段幅频特性Fig.4 Amplitude-frequency characteristic of transient zero-sequence current at high frequency
由图4 可知,主谐振频率接近1 kHz 且远大于其他谐振频率下的能量,与故障瞬间较大的冲击能量相对应。因此,本文以暂态过程中主谐振分量能量最大原理来优化参数K。根据第6.1节仿真模型所获得的故障零序电流对VMD关键参数寻优过程进行具体分析。K取不同值时,对故障零序电流信号进行VMD,各IMF分量如图5所示。
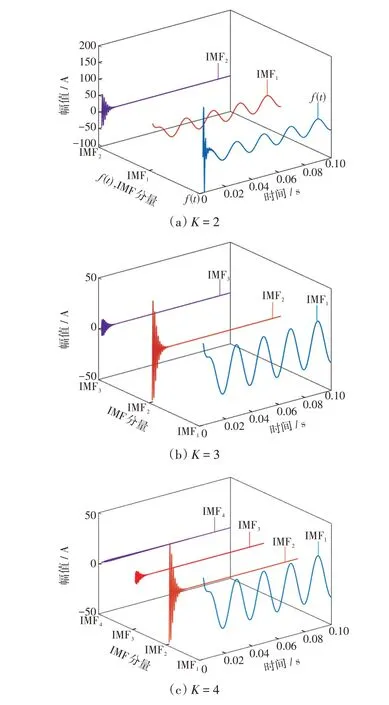
图5 不同K 值下故障零序电流分解Fig.5 Decomposition of fault zero-sequence current under different values of K
由图5(a)可知,当K=2 时,IMF1为稳态工频分量与衰减直流分量的叠加,IMF2为暂态主频分量;随着K值的增大,分解得到的IMF1和IMF2与K=2时结果相同,但出现了幅值更小的高频分量。由于各IMF分量为单一频率信号,故采用快速傅里叶变换来衡量IMF分量的能量大小,结果如图6所示。
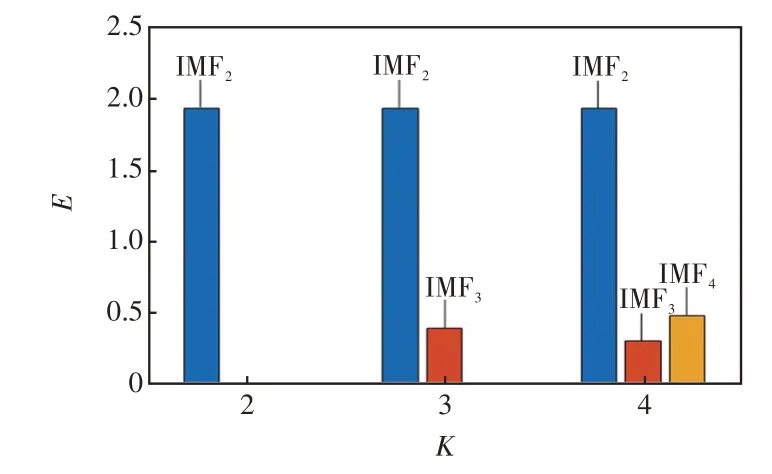
图6 不同K 值下各IMF 分量能量对比Fig.6 Comparison of IMF component energy under different values of K
从图6 可以看出,当K=3 时IMF2的能量E大于IMF3且与K=2 时IMF2的能量相同;当K=4时,IMF2仍为能量最大的分量,IMF3和IMF4的能量均远小于IMF2。综合以上分析可以得出,最优参数K=2。在最优参数K下,经VMD二次分解可以得到故障零序电流的暂态主频分量、衰减直流分量和稳态工频分量。
3 故障特征量的构造
3.1 衰减直流分量衰减速度
为了描述故障线路上不同检测点故障零序电流中衰减直流分量的差异,定义衰减速度Kup为
式中:|I2-1.up|>|I2-1.down|;I2-1.up为故障点上游区段衰减直流分量;I2-1.down为故障点下游区段衰减直流分量;|I2-1.up|、|I2-1.down|分别为故障点上游、下游区段故障零序电流衰减直流分量的幅值;|I2-1.up|max、|I2-1.up|min分别为故障点上游区段故障零序电流衰减直流分量幅值的最大值和最小值;t1.max、t2.max分别为最大值和最小值对应的时刻。
3.2 暂态主频分量峰值与稳态工频分量幅值比
当谐振接地系统发生单相接地故障时,故障点下游健全区段两端检测点的暂态主频分量峰值与稳态工频分量幅值比严格相等[17]。故障点下游、上游的暂态主频分量峰值与稳态工频分量幅值的比值分别为
式中:ωl、ωb分别为故障点上游和下游的暂态主谐振频率;C1为健全线路和故障点上游线路的等值电容;C2为故障点下游线路的等值电容。
故障点上游健全区段由于消弧线圈电感电流对暂态零序电流稳态工频分量的补偿作用,使得故障点上游健全区段相邻检测点比值不再相等,且故障区段相邻检测点比值更大。基于此差异,可构造故障特征量实现故障区段的准确定位。
3.3 暂态主频分量与衰减直流分量能量比
为了考虑衰减直流分量在小角度故障时能量占比大的情况,引入暂态主频分量与衰减直流分量能量比来衡量故障点上下游暂态零序电流在不同故障初相角的能量差异。。
t时刻IMF分量所具有的瞬时能量E(t)为
式中,A(t)为IMF分量在t时刻的瞬时值。
单相接地故障过程的暂态能量函数为
考虑到衰减直流分量与暂态主频分量的衰减时间不同,本文选取不同的数据窗进行能量计算,衰减直流分量选取5个工频周期,暂态主频分量选取1个工频周期。
3.4 相邻检测点故障零序电流波形差异系数
相关系数法忽略了信号幅值对波形相似度的影响。在谐振接地系统中由于消弧线圈的存在,故障线路各区段稳态工频分量极性相同,均从母线流向线路,如图1所示。由于故障点上下游线路长度存在较大差别,因此故障点上下游故障零序电流波形存在明显差异。本文采用DTW衡量各区段故障零序电流波形的差异。DTW的计算公式[18]为
式中:I1、I2为相邻检测点的故障零序电流;P为路径空间,P={p1,p2,…,ps,…,pk} ;元素ps为路径上第s个点的坐标;k为所有路径中元素的总数;DTW为距离计算值。
通过1 个积累距离矩阵可求得两时间序列的DTW(I1,I2),便于实现。为了消除线路参数对健全区段两端检测点故障零序电流的影响,对DTW 进行归一化处理,即
式中:D*TW为经过归一化的距离计算值;i1r、i2j分别为时间序列I1、I2的某一瞬时值;m、n为两时间序列的数据长度。
3.5 相邻检测点暂态主频分量极性比
由于消弧线圈的补偿作用,故障线路各区段暂态零序电流中稳态工频分量的流向一致,均是从母线流向故障点,无法准确判断故障区段。结合对暂态零序电流的分析,故障点上游各区段零序电流暂态主频分量幅值较大且初始方向与健全线路、故障点下游线路相反。本文采用差分方法判断相邻检测点故障零序电流暂态主频分量的初始极性pk,k+1,可表示为
式中:x(n0)为某一点的瞬时值;n0为差分计算的起始采样点;diff(i)为暂态主频分量的一阶差分测度;sgn(diff(ik))为各检测点暂态主频分量一阶差分的符号。
4 理论分析
4.1 SVM 基本原理
SVM能提供良好的泛化性能,已被广泛应用于小样本分类中[19]。故障定位问题中作为经典的非线性问题,SVM无法在原始样本空间中找到分类超平面,需引入核函数K( )xi,xj映射到高维空间线性可分。本文采用高斯核函数映射变换,其表达式为
式中:xi、xj为样本向量;‖xi-xj‖2为xi和xj之间距离的平方;γ为核函数本身的超参数。
引入松弛变量度量训练集中单个样本违背约束的程度,得到软间隔核化SVM的基本型,即
式中:ξi为松弛变量;c为惩罚因子;xi为输入的第i个样本;yi为样本类型;ω为SVM 的自身参数;ϕ(xi)为映射后的样本向量。
引入拉格朗日惩罚因子α,最终得到软间隔高斯核SVM的对偶型,即
式中:αi和αj为惩罚参数;γ和c为两个需要预先设定的超参数。由式(17)可知,SVM模型中超参数γ和c设定值直接决定了SVM 的最终分类效果。当c较大时,分类边界会倾向于复杂,最大间隔带的宽度较小,支持向量由较少的样本组成;当c较小时,支持向量由多个不满足大间隔约束的样本组成。超参数γ可以近似认为控制每个支持向量的影响范围。
4.2 改进鲸鱼优化算法
为克服传统优化算法易陷入局部最优的问题,采用IWOA[20]对SVM的两个超参数寻优。
为了提高种群的复杂性,在传统WOA中,引入混沌理论生成初始状态的种群,其表达式为
同时,在鲸鱼位置更新后增加反馈阶段,通过交流学习使种群中最差鲸鱼能快速运动到食物附近,提高算法的收敛速度,其表达式为
式中:Xwor-new为更新后的位置向量;Xwor为种群中最差鲸鱼个体位置向量;Xp为随机选择的个体;r为0~1之间的随机数。
此外,在收缩包围机制和螺旋更新位置数学模型中引入自适应惯性权重,进一步改善算法的优化性能。
自适应惯性权重w的表达式为
式中:f(x)为适应度函数,本文选取测试集的分类准确率作为适应度函数;u为第1 次迭代种群中的最优值;n1为当前的迭代次数。
最终得到的位置更新公式为
式中:Xp(t)为猎物位置向量;X(t)为当前鲸鱼位置向量;A0和C0为系数向量;D0为鲸鱼与猎物之间的距离;b为1个常数;l为[-1,1]内的随机数。
随着迭代次数增加,适应度值与惯性权重近似成反比,保证了惯性权重的自适应性,很大程度上提高了算法的全局优化能力。
5 区段定位流程
故障区段定位流程如图7所示,具体步骤如下。
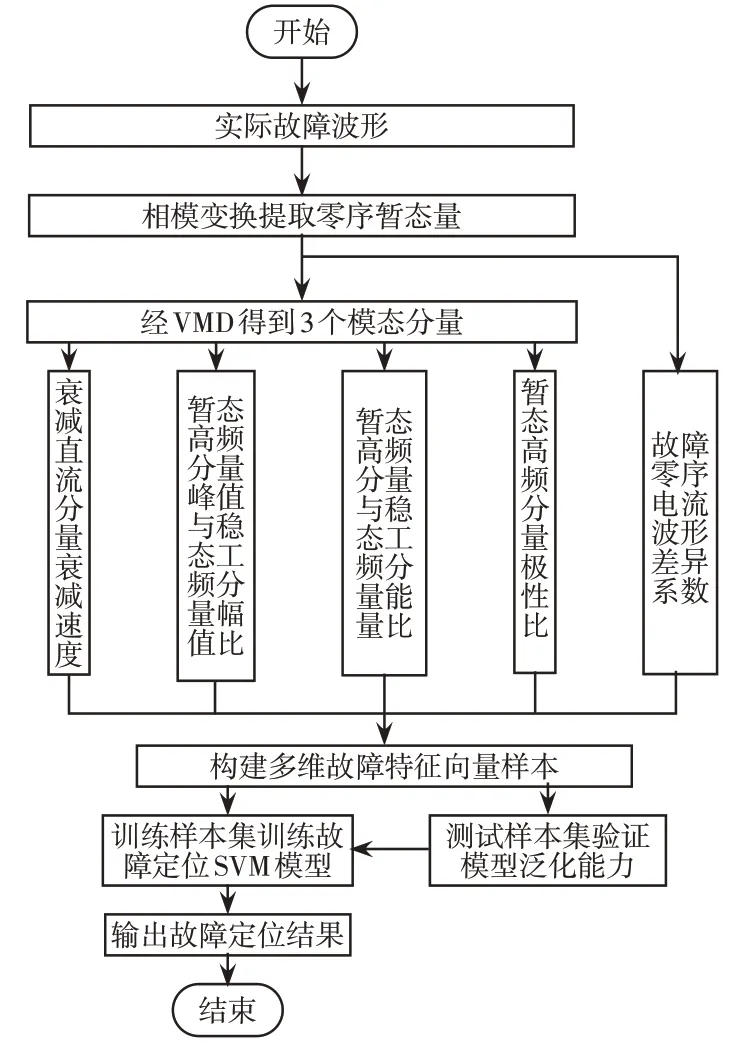
图7 故障定位流程Fig.7 Flow chart of fault location
步骤1判定发生故障后,利用各检测点故障指示器提取故障线路各区段的电流波形,采样时间为0.1 s,采样频率为10 kHz,
步骤2采用自适应VMD暂态零序电流,获得多组IMF分量。
步骤3结合时域波形及频域分解得到各模态分量,构建5个特征量。
步骤4计算各区段的多维特征量,构建用于SVM分类模型的输入特征向量。
步骤5改变故障初相角、过渡电阻等故障条件,获得多组故障样本,按照高阻和低阻接地的发生概率比划分训练集和测试集,验证故障区段定位效果。
6 仿真分析
6.1 模型搭建
在ATP/EMTP 中搭建10 kV小电流接地系统仿真模型[21],如图8 所示。设消弧线圈脱谐度为8%,计算可得Lp=0.25 H;消弧线圈本身阻值为感抗的2%,RL=1.57 Ω。线路参数如表1所示。
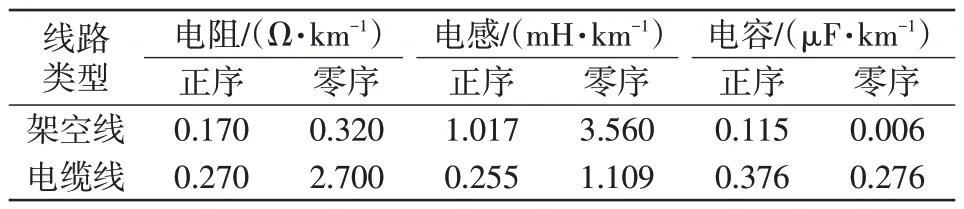
表1 线路阻抗参数Tab.1 Line impedance parameters
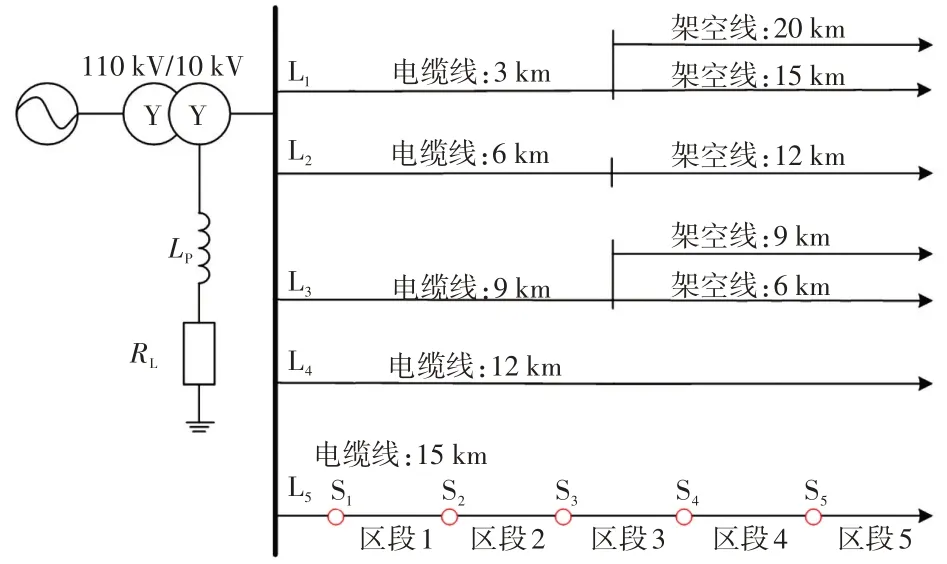
图8 谐振圈接地系统仿真模型Fig.8 Simulation model of resonant coil grounding system
模拟不同过渡电阻、故障初相角和故障位置下单相接地故障时的故障零序电流,提取故障特征,获得300组故障样本。按照7∶3的比例划分训练集和测试集,为了符合实际情况下低阻与高阻接地发生概率不同的情况,在210组训练样本中设置低阻接地故障样本为150 组、高阻接地故障样本为50组、另外10组样本随机选取的方式。以区段编号作为分类目标,区段1为第1种分类结果,区段2为第2种分类结果,以此类推,区段5为第5种分类结果。
6.2 SVM 参数寻优
分别采用WOA和IWOA对SVM的两个超参数γ和c进行优化,设置种群个数为20,最大迭代次数为100,γ∈[0.01,10] ,c∈[0.1,100] 。两种算法的适应度迭代曲线如图9所示。表2给出了两种算法性能对比结果。可以看出,IWOA 的运行时间比WOA少1.39 s,最佳适应度迭代次数两种算法相差不大,但IWOA 的平均适应度收敛速度明显快于WOA。经IWOA-SVM模型训练10次后得到的平均最优值为c=3.669 3、γ=1.148 7,此参数下训练模型分类准确率为98.89%;经WOA-SVM模型训练10次得到的平均最优值为c=12.256 9、γ=0.653 4,此参数下训练模型的分类准确率为96.67%。

表2 两种算法性能对比Tab.2 Comparison of performance between two methods
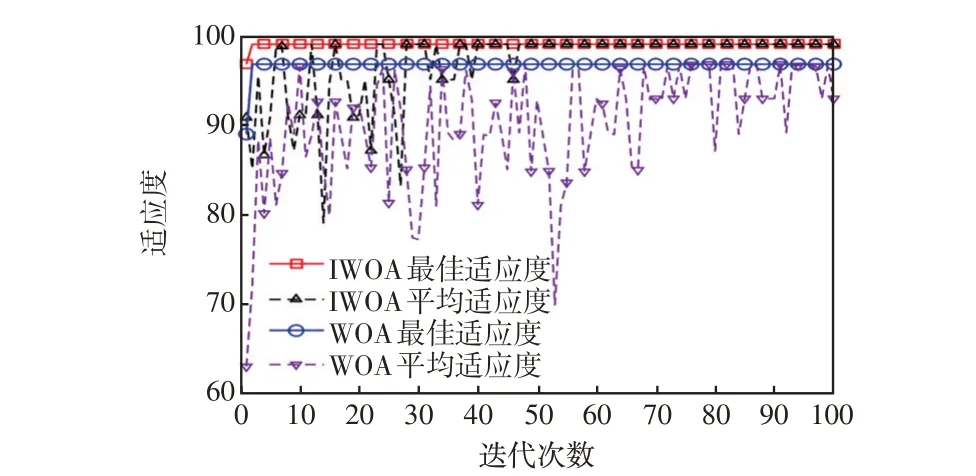
图9 两种SVM 参数寻优算法的适应度迭代曲线Fig.9 Fitness iteration curves of two SVM parameter optimization algorithms
6.2 结果分析
在最优参数c和γ下得到IWOA-SVM 故障定位分类模型,测试集分类准确率达到98.89%,测试集分类结果如图10所示。
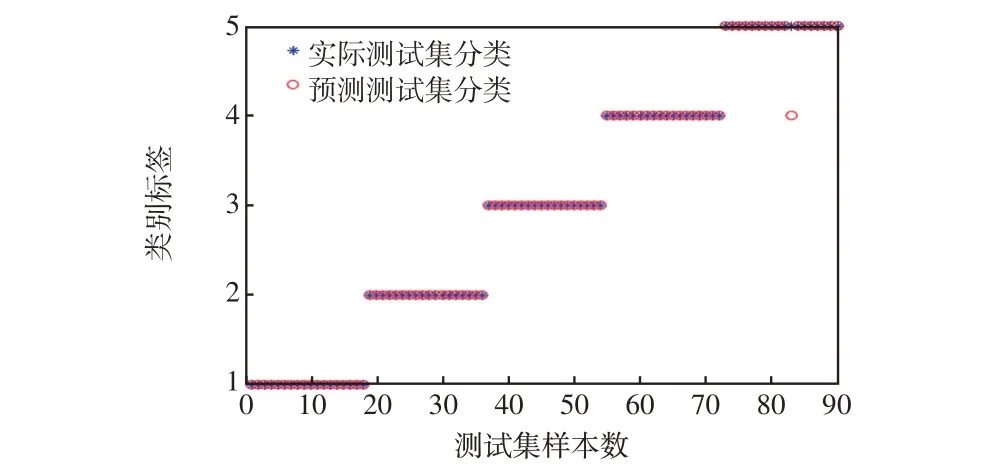
图10 测试集分类结果Fig.10 Classification results of test set
在故障线路末端靠近负荷侧发生高阻接地故障时,由于故障初相角为90°时衰减直流分量较小,加之上游检测点采集的暂态零序电流幅值较小且含噪声造成特征不明显,从而出现误选问题。不同特征向量分类准确率对比如图11 所示。可以看出,特征1~5的定位正确率依次为84.44%、87.78%、92.22%、94.44%、95.56%,相比于特征融合的SVM分类模型定位正确率分别降低了14.45%、11.11%、6.67%、4.45%、3.33%。
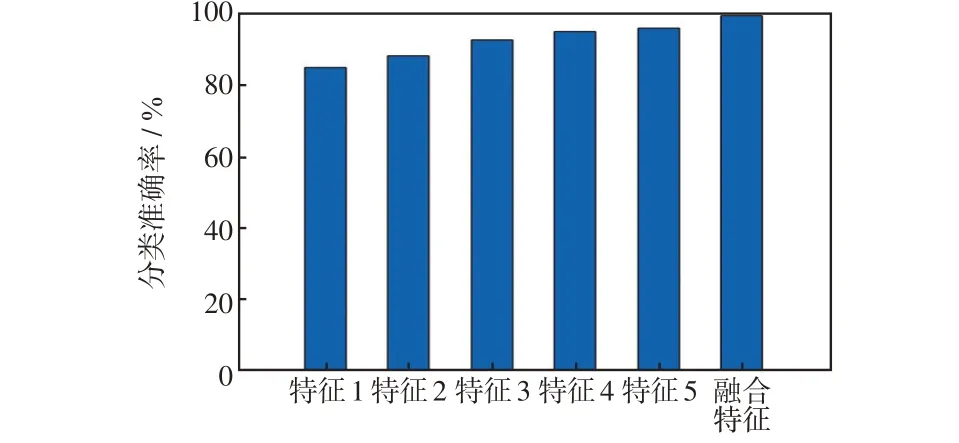
图11 不同特征向量分类准确率对比Fig.11 Comparison of classification accuracy among different feature vectors
7 结 论
本文以暂态过程中故障信息为依据,结合SVM提出了一种多特征融合的单相接地故障区段检测方法。主要结论如下。
(1)基于暂态零序电流在故障线路各区段的差异,构造了5 个特征量用于故障定位,即衰减直流分量衰减速度、暂态主频分量峰值与稳态工频分量幅值比、暂态主频分量与衰减直流分量能量比、相邻检测点故障零序电流波形差异系数、相邻检测点暂态主频分量极性比。
(2)采用IWOA 优化SVM 的关键参数,融合多个时频特征量构成高维特征向量,得到用于故障定位的分类模型。
(3)通过仿真分析验证了本文所提定位方法在不同故障条件下的适用性。所提方法的故障定位正确率相比于利用不同单一特征量的定位方法均有不同程度的提高,且在小初相角、高阻接地等极限故障情况下能准确定位故障区段,可靠性高。
由于VMD的分解效果受1个关键参数(即惩罚因子α)的影响较大,适用于暂态零序电流分解的最优值有待研究。同时,实际配电网中还存在电弧接地等情况,本文所提方法的适用性还需进一步验证。
